Abstract
We propose an information-theoretically secure encryption scheme for classical messages with quantum ciphertexts that offers detection of eavesdropping attacks, and re-usability of the key in case no eavesdropping took place: the entire key can be securely re-used for encrypting new messages as long as no attack is detected. This is known to be impossible for fully classical schemes, where there is no way to detect plain eavesdropping attacks.
This particular application of quantum techniques to cryptography was originally proposed by Bennett, Brassard and Breidbart in 1982, even before proposing quantum-key-distribution, and a simple candidate scheme was suggested but no rigorous security analysis was given. The idea was picked up again in 2005, when Damgård, Pedersen and Salvail suggested a new scheme for the same task, but now with a rigorous security analysis. However, their scheme is much more demanding in terms of quantum capabilities: it requires the users to have a quantum computer.
In contrast, and like the original scheme by Bennett et al., our new scheme requires from the honest users merely to prepare and measure single BB84 qubits. As such, we not only show the first provably-secure scheme that is within reach of current technology, but we also confirm Bennett et al.’s original intuition that a scheme in the spirit of their original construction is indeed secure.
L. Salvail—Funded by Canada’s NSERC discovery grant and NSERC discovery accelerator.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Background. Classical information-theoretic encryption (like the one-time pad) and authentication (like Carter-Wegman authentication) have the serious downside that the key can be re-used only a small number of times, e.g. only once in case of the one-time pad for encryption or a strongly universal\(_2\) hash function for authentication. This is inherent since by simply observing the communication, an eavesdropper Eve inevitably learns a substantial amount of information on the key. Furthermore, there is no way for the communicating parties, Alice and Bob, to know whether Eve is present and has observed the communication or not, so they have to assume the worst.
This situation changes radically when we move to the quantum setting and let the ciphertext (or authentication tag) be a quantum state: then, by the fundamental properties of quantum mechanics, an Eve that observes the communicated state inevitably changes it, and so it is potentially possible for the receiver Bob to detect this, and, vice versa, to conclude that the key is still secure and thus can be safely re-used in case everything looks as it is supposed to be.
This idea of key re-usability by means of a quantum ciphertext goes back to a manuscript titled “Quantum Cryptography II: How to re-use a one-time pad safely even if \(P=NP\)” by Bennett, Brassard and Breidbart written in 1982. However, their paper was originally not published, and the idea was put aside after two of the authors discovered what then became known as BB84 quantum-key-distribution [2].Footnote 1 Only much later in 2005, this idea was picked up again by Damgård, Pedersen and Salvail in [5] (and its full version in [6]), where they proposed a new such encryption scheme and gave a rigorous security proof — in contrast, Bennett et al.’s original reasoning was very informal and hand-wavy.
The original scheme by Bennett et al. is simple and natural: you one-time-pad encrypt the message, add some redundancy by encoding the ciphertext using an error correction (or detection) code, and encode the result bit-wise into what we nowadays call BB84 qubits. The scheme by Damgård et al. is more involved; in particular, the actual quantum encoding is not done by means of single qubits, but by means of states that form a set of mutually unbiased bases in a Hilbert space of large dimension. This in particular means that their scheme requires a quantum computer to produce the quantum ciphertexts and to decrypt them.
Our Results. We are interested in the question of whether one can combine the simplicity of the originally proposed encryption scheme by Bennett et al. with a rigorous security analysis as offered by Damgård et al. for their scheme; in particular, whether there is a provably secure scheme that is within reach of being implementable with current technology — and we answer the question in the affirmative.
We start with the somewhat simpler problem of finding an authentication scheme that allows to re-use the key in case no attack is detected, and we show a very simple solution. In order to authenticate a (classical) message \(msg\), we encode a random bit string \(x \in \{0,1\}^n\) into BB84 qubits \(H^\theta {|x\rangle }\), where \(\theta \in \{0,1\}^n\) is part of the shared secret key, and we compute a tag \(t = \mathsf{MAC}(k,msg\Vert x)\) of the message concatenated with x, where \(\mathsf{MAC}\) is a classical information-theoretic one-time message authentication code, and its key k is the other part of the shared secret key. The qubits \(H^\theta {|x\rangle }\) and the classical tag t are then sent along with \(msg\), and the receiver verifies correctness of the received message in the obvious way by measuring the qubits to obtain x and checking t.
One-time security of the scheme is obvious, and the intuition for key-recycling is as follows. Since Eve does not know \(\theta \), she has a certain minimal amount of uncertainty in x, so that, if \(\mathsf{MAC}\) has suitable extractor-like properties, the tag t is (almost) random and independent of k and \(\theta \), and thus gives away no information on k and \(\theta \). Furthermore, if Eve tries to gain information on k and \(\theta \) by measuring some qubits, she disturbs these qubits and is likely to be detected. A subtle issue is that if Eve measures only very few qubits then she has a good chance of not being detected, while still learning a little bit on \(\theta \) by the fact that she has not been detected. However, as long as her uncertainty in \(\theta \) is large enough this should not help her (much), and the more information on \(\theta \) she tries to collect this way the more likely it is that she gets caught.
We show that the above intuition is correct. Formally, we prove that as long as the receiver Bob accepts the authenticated message, the key-pair \((k,\theta )\) can be safely re-used, and if Bob rejects, it is good enough to simply refresh \(\theta \). Our proof is based on techniques introduced in [19] and extensions thereof.
Extending our authentication scheme to an encryption scheme is intuitively quite easy: we simply extract a one-time-pad key from x, using a strong extractor (with some additional properties) with a seed that is also part of the shared secret key. Similarly to above, we can prove that as long as the receiver Bob accepts, the key can be safely re-used, and if Bob rejects it is good enough to refresh \(\theta \).
In our scheme, the description lengthFootnote 2 of \(\theta \) is \(m + 3\lambda \), where m is the length of the encrypted message \(msg\) and \(\lambda \) is the security parameter (so that the scheme fails with probability at most \(2^{-\lambda }\)). Thus, with respect to the number of fresh random bits that are needed for the key refreshing, i.e. for updating the key in case Bob rejects, our encryption scheme is comparable to the scheme by Damgård et al. Footnote 3 and optimal in terms of the dependency on the message length m.
Our schemes can be made noise robust in order to deal with a (slightly) noisy quantum communication; the generic solution proposed in [5, 6] of using a quantum error correction code is not an option for us as it would require a quantum computer for en- and decoding. Unfortunately, using straightforward error correction techniques, like sending along the syndrome of x with respect to a suitable error correcting code, renders our proofs invalid beyond an easy fix, though it is unclear whether the scheme actually becomes insecure. However, we can deal with the issue by means of using error correction “without leaking partial information”, as introduced by Dodis and Smith [8] and extended to the quantum setting by Fehr and Schaffner [9]. Doing error correction in a more standard way, which would offer more freedom in choosing the error correction code and allow for a larger amount of noise, remains an interesting open problem.
Encryption with Key Recycling vs QKD. A possible objection against the idea of encryption with key recycling is that one might just as well use QKD to produce a new key, rather than re-using the old one. However, there are subtle advantages of using encryption with key recycling instead. For instance, encryption with key recycling is (almost) non-interactive and requires only 1 bit of authenticated feedback: “accept” or “reject”, that can be provided offline, i.e., after the communication of the private message, as long as it is done before the scheme is re-used. This opens the possibility to provide the feedback by means of a different channel, like by confirming over the phone. In contrast, for QKD, a large amount of data needs to be authenticated online and in both directions. If no physically authenticated channel is available, then the authenticated feedback can actually be done very easily: Alice appends a random token to the message she communicates to Bob in encrypted form, and Bob confirms that no attack is detected by returning the token back to Alice — in plain — and in case he detected an attack, he sends a reject message instead.Footnote 4 Furthermore, encryption with key recycling has the potential to be more efficient than QKD in terms of communication. Even though this is not the case for our scheme, there is certainly potential, because no sifting takes place and hence there is no need to throw out a fraction of the quantum communication. Altogether, on a stable quantum network for instance, encryption with key-recycling would be the preferred choice over QKD. Last but not least, given that the re-usability of a one-time-pad-like encryption key was one of the very first proposed applications of quantum cryptography — even before QKD — we feel that giving a satisfactory answer should be of intellectual interest.
Related Work. Besides the work of Brassard et al. and of Damgård et al., who focus on encrypting classical messages, there is a line of work, like [11, 13, 15], that considers key recycling in the context of authentication and/or encryption of quantum messages. However, common to almost all this work is that only part of the key can be re-used if no attack is detected, or a new but shorter key can be extracted. The only exceptions we know of are the two recent works by Garg et al. [10] and by Portmann [16], which consider and analyze authentication schemes for quantum messages that do offer re-usability of the entire key in case no attack is detected. However, these schemes are based on techniques (like unitary designs) that require the honest users to perform quantum computations also when restricting to classical messages. Actually, [16] states it as an explicit open problem to “find a prepare-and-measure scheme to encrypt and authenticate a classical message in a quantum state, so that all of the key may be recycled if it is successfully authenticated”. On the other hand, their schemes offer security against superposition attacks, where the adversary may trick the sender into authenticating a superposition of classical messages; this is something we do not consider here — as a matter of fact, it would be somewhat unnatural for us since such superposition attacks require the sender (wittingly or unwittingly) to hold a quantum computer, which is exactly what we want to avoid.
2 Preliminaries
2.1 Basic Concepts of Quantum Information Theory
We assume basic familiarity; we merely fix notation and terminology here.
Quantum states. The state of a quantum system with state space \(\mathcal {H}\) is specified by a state vector \({|\varphi \rangle } \in \mathcal {H}\) in case of a pure state, or, more generally in case of a mixed state, by a density matrix \(\rho \) acting on \(\mathcal {H}\). The set of density matrices acting on \(\mathcal {H}\) is denoted \(\mathcal{D}(\mathcal {H})\). We typically identify different quantum systems by means of labels \({{{\textsf {\textit{A}}}}},{{{\textsf {\textit{B}}}}}\) etc., and we write \(\rho _{{{\textsf {\textit{A}}}}}\) for the state of system \({{{\textsf {\textit{A}}}}}\) and \(\mathcal {H}_{{{\textsf {\textit{A}}}}}\) for its state space, etc. The joint state of a bipartite system \({{{\textsf {\textit{A}}}}}{{{\textsf {\textit{B}}}}}\) is given by a density matrix \(\rho _{{{{\textsf {\textit{A}}}}}{{{\textsf {\textit{B}}}}}}\) in \(\mathcal{D}(\mathcal {H}_{{{\textsf {\textit{A}}}}}\otimes \mathcal {H}_{{{\textsf {\textit{B}}}}})\); it is then understood that \(\rho _{{{{\textsf {\textit{A}}}}}}\) and \(\rho _{{{{\textsf {\textit{B}}}}}}\) are the respective reduced density matrices \(\rho _{{{{\textsf {\textit{A}}}}}} = \mathrm {tr}_{{{\textsf {\textit{B}}}}}(\rho _{{{{\textsf {\textit{A}}}}}{{{\textsf {\textit{B}}}}}})\) and \(\rho _{{{{\textsf {\textit{B}}}}}} = \mathrm {tr}_{{{\textsf {\textit{A}}}}}(\rho _{{{{\textsf {\textit{A}}}}}{{{\textsf {\textit{B}}}}}})\).
We also consider states that consist of a classical and a quantum part. Formally, \(\rho _{X{{{\textsf {\textit{E}}}}}} \in \mathcal{D}(\mathcal {H}_X \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\) is called a cq-state (for classical-quantum), if it is of the form
where \(P_X: \mathcal{X} \rightarrow [0,1]\) is a probability distribution, \(\{{|x\rangle }\}_{x \in \mathcal X}\) is a fixed orthonormal basis of \(\mathcal {H}_X\), and \(\rho _{{{\textsf {\textit{E}}}}}^x \in \mathcal{D}(\mathcal {H}_{{{\textsf {\textit{E}}}}})\). Throughout, we will slightly abuse notation and express this by writing \(\rho _{X{{{\textsf {\textit{E}}}}}} \in \mathcal{D}(\mathcal{X} \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\).
In the context of such a cq-state \(\rho _{X{{{\textsf {\textit{E}}}}}}\), an event \(\varLambda \) is specified by means of a decomposition \(\rho _{X{{{\textsf {\textit{E}}}}}} = P[\varLambda ] \cdot \rho _{X{{{\textsf {\textit{E}}}}}|\varLambda } + P[\lnot \varLambda ] \cdot \rho _{X{{{\textsf {\textit{E}}}}}|\lnot \varLambda }\) with \(P[\varLambda ],P[\lnot \varLambda ] \ge 0\) and \(\rho _{X{{{\textsf {\textit{E}}}}}|\varLambda },\rho _{X{{{\textsf {\textit{E}}}}}|\lnot \varLambda }\in \mathcal{D}(\mathcal{X} \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\). Associated to such an event \(\varLambda \) is the indicator random variable \(1_{\!\varLambda }\), i.e., the cq-state \(\rho _{X 1_{\!\varLambda } {{{\textsf {\textit{E}}}}}} \in \mathcal{D}(\mathcal{X} \otimes \{0,1\} \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\), defined in the obvious way. Note that, for any cq-state \(\rho _{X{{{\textsf {\textit{E}}}}}}\) and any \(x \in \mathcal X\), the event \(X\!=\!x\) is naturally defined and \(\rho _{X{{{\textsf {\textit{E}}}}}|X=x} = {|x\rangle }{\langle x|} \otimes \rho _{{{\textsf {\textit{E}}}}}^x\) and \(\rho _{{{{\textsf {\textit{E}}}}}|X=x} = \rho _{{{\textsf {\textit{E}}}}}^x\).
If a state \(\rho _{X}\) is purely classical, meaning that \(\rho _{X} = \sum _x P_X(x) {|x\rangle }{\langle x|}\) and expressed as \(\rho _{X} \in \mathcal{D}(\mathcal{X})\), we may refer to standard probability notation so that probabilities like \(P[X\!=\!x]\) are well understood. Finally, we write \(\mu _\mathcal{X}\) for the fully mixed state  .
.
General quantum operations. Operations on quantum systems are described by CPTP maps. To emphasize that a CPTP map \(\mathcal {Q}: \mathcal{D}(\mathcal {H}_{{{\textsf {\textit{A}}}}}) \rightarrow \mathcal{D}(\mathcal {H}_{{{{\textsf {\textit{A}}}}}'})\) acts on density matrices in \(\mathcal{D}(\mathcal {H}_{{{\textsf {\textit{A}}}}})\), we sometimes write \(\mathcal {Q}_{{{\textsf {\textit{A}}}}}\), and we say that it “acts on \({{{\textsf {\textit{A}}}}}\)”. Also, we may write \(\mathcal {Q}_{{{{\textsf {\textit{A}}}}}\rightarrow {{{\textsf {\textit{A}}}}}'}\) in order to be explicit about the range too. If \(\mathcal Q\) is a CPTP map acting on \({{{\textsf {\textit{A}}}}}\), we often abuse notation and simply write \(\mathcal{Q}_{{{\textsf {\textit{A}}}}}(\rho _{{{{\textsf {\textit{A}}}}}{{{\textsf {\textit{B}}}}}})\) or \(\rho _{\mathcal{Q}({{{\textsf {\textit{A}}}}}){{{\textsf {\textit{B}}}}}}\) for \(\bigl (\mathcal{Q}_{{{\textsf {\textit{A}}}}}\otimes id_{{{\textsf {\textit{B}}}}}\bigr )(\rho _{{{{\textsf {\textit{A}}}}}{{{\textsf {\textit{B}}}}}})\), where \(id_{{{\textsf {\textit{B}}}}}\) is the identity map on \(\mathcal{D}(\mathcal {H}_{{{\textsf {\textit{B}}}}})\).
In line with our notation for cq-states, \(\mathcal {Q}: \mathcal{D}(\mathcal{X} \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}}) \rightarrow \mathcal{D}(\mathcal{X}' \otimes \mathcal {H}_{{{{\textsf {\textit{E}}}}}'})\) is used to express that \(\mathcal {Q}\) maps any cq-state \(\rho _{X{{{\textsf {\textit{E}}}}}} \in \mathcal{D}(\mathcal{X} \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\) to a cq-state \(\mathcal {Q}(\rho _{X'{{{\textsf {\textit{E}}}}}})\) in \(\mathcal{D}(\mathcal{X}' \otimes \mathcal {H}_{{{{\textsf {\textit{E}}}}}'})\). We say that a CPTP map \(\mathcal {Q}: \mathcal{D}(\mathcal{X} \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}}) \rightarrow \mathcal{D}(\mathcal{X} \otimes \mathcal {H}_{{{{\textsf {\textit{E}}}}}'})\) is “controlled by X and acts on \({{{\textsf {\textit{E}}}}}\,\)” if on a cq-state \(\rho _{X{{{\textsf {\textit{E}}}}}}\in \mathcal{D}(\mathcal{X} \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\) it acts as
with “conditional” CPTP maps \(\mathcal {Q}^x: \mathcal{D}(\mathcal {H}_{{{\textsf {\textit{E}}}}}) \rightarrow \mathcal{D}(\mathcal {H}_{{{{\textsf {\textit{E}}}}}'})\). Note that in this case we write \(\mathcal {Q}_{X{{{\textsf {\textit{E}}}}}\rightarrow {{{\textsf {\textit{E}}}}}'}\) rather than \(\mathcal {Q}_{X{{{\textsf {\textit{E}}}}}\rightarrow X{{{\textsf {\textit{E}}}}}'}\), as it is understood that \(\mathcal {Q}\) keeps X alive. For concreteness, we require that such a \(\mathcal {Q}\) is of the form \(\mathcal {Q} = \sum _x \mathcal{P}_{{|x\rangle }{\langle x|}} \otimes \mathcal {Q}^x\) where \(\mathcal{P}_{{|x\rangle }{\langle x|}}(\rho ) = {|x\rangle }{\langle x|}\,\rho \, {|x\rangle }{\langle x|}\) for any \(\rho \in \mathcal{D}(\mathcal {H}_X)\).Footnote 5 As such, \(\mathcal {Q}\) is fully specified by means of the conditional CPTP maps \(\mathcal {Q}^x\). Finally, for any function \(f:\mathcal{X} \rightarrow \mathcal{Y}\), we say that \(\mathcal {Q}: \mathcal{D}(\mathcal{X} \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}}) \rightarrow \mathcal{D}(\mathcal{X} \otimes \mathcal {H}_{{{{\textsf {\textit{E}}}}}'})\) is “controlled by f(X)” if it is controlled by X, but \(\mathcal {Q}^x = \mathcal {Q}^{x'}\) for any \(x,x' \in \mathcal X\) with \(f(x) = f(x')\).
Markov-chain states. Let \(\rho _{XY{{{\textsf {\textit{E}}}}}} \in \mathcal{D}(\mathcal{X} \otimes \mathcal{Y} \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\) be a cq-state with two classical subsystems X and Y. Following [7], we define \(\rho _{X\leftrightarrow Y\leftrightarrow {{{\textsf {\textit{E}}}}}}\) to be the “Markov-chain state”
with \(\rho _{{{\textsf {\textit{E}}}}}^y = \sum _x P_{X|Y}(x|y)\, \rho _{{{\textsf {\textit{E}}}}}^{x,y}\). If the state \(\rho _{XY{{{\textsf {\textit{E}}}}}}\) is clear from the context we write \(X\leftrightarrow Y\leftrightarrow {{{\textsf {\textit{E}}}}}\) to express that \(\rho _{XY{{{\textsf {\textit{E}}}}}} = \rho _{X\leftrightarrow Y\leftrightarrow {{{\textsf {\textit{E}}}}}}\). It is an easy exercise to verify that the Markov-chain condition \(X\leftrightarrow Y\leftrightarrow {{{\textsf {\textit{E}}}}}\) holds if and only if  for a CPTP map
for a CPTP map  that is controlled by Y and acts on the “empty” system \(\varnothing \), i.e., the conditional maps act as
that is controlled by Y and acts on the “empty” system \(\varnothing \), i.e., the conditional maps act as  .
.
Quantum measurements. We model a measurement of a quantum system \({{{\textsf {\textit{A}}}}}\) with outcome in \(\mathcal X\) by means of a CPTP map \(\mathcal {M}: \mathcal{D}(\mathcal {H}_{{{\textsf {\textit{A}}}}}) \rightarrow \mathcal{D}(\mathcal{X})\) that acts as
where \(\{{|x\rangle }\}_{x \in \mathcal X}\) is a fixed basis, and \(\{ E_x \}_{x \in \mathcal X}\) forms a POVM, i.e., a family of positive-semidefinite operators that add up to the identity matrix  . A measurement \(\mathcal{M}: \mathcal{D}(\mathcal{Z} \otimes \mathcal {H}_{{{\textsf {\textit{A}}}}}) \rightarrow \mathcal{D}(\mathcal{Z} \otimes \mathcal{X})\) is said to be a “measurement of \({{{\textsf {\textit{A}}}}}\) controlled by Z” if it is controlled by Z and acts on \({{{\textsf {\textit{A}}}}}\) as a CPTP map. It is easy to see that in this case the conditional CPTP maps \(\mathcal{M}^z: \mathcal{D}(\mathcal {H}_{{{\textsf {\textit{A}}}}}) \rightarrow \mathcal{D}(\mathcal{X})\) are measurements too, referred to as “conditional measurements”.
. A measurement \(\mathcal{M}: \mathcal{D}(\mathcal{Z} \otimes \mathcal {H}_{{{\textsf {\textit{A}}}}}) \rightarrow \mathcal{D}(\mathcal{Z} \otimes \mathcal{X})\) is said to be a “measurement of \({{{\textsf {\textit{A}}}}}\) controlled by Z” if it is controlled by Z and acts on \({{{\textsf {\textit{A}}}}}\) as a CPTP map. It is easy to see that in this case the conditional CPTP maps \(\mathcal{M}^z: \mathcal{D}(\mathcal {H}_{{{\textsf {\textit{A}}}}}) \rightarrow \mathcal{D}(\mathcal{X})\) are measurements too, referred to as “conditional measurements”.
Note that whenever \(\mathcal{M}: \mathcal{D}(\mathcal {H}_Z \otimes \mathcal {H}_{{{\textsf {\textit{A}}}}}) \rightarrow \mathcal{D}(\mathcal{X})\) is an arbitrary measurement of Z and \({{{\textsf {\textit{A}}}}}\) that is applied to a cq-state \(\rho _{Z{{{\textsf {\textit{A}}}}}} \in \mathcal{D}(\mathcal{Z} \otimes \mathcal {H}_{{{\textsf {\textit{A}}}}})\), we may assume that \(\mathcal{M}\) first “produces a copy of Z”, and thus we may assume without loss of generality that \(\mathcal{M}: \mathcal{D}(\mathcal{Z} \otimes \mathcal {H}_{{{\textsf {\textit{A}}}}}) \rightarrow \mathcal{D}(\mathcal{Z} \otimes \mathcal{X})\) is controlled by Z.
For a given  ,
,  denotes the BB84 measurement of an n-qubit system \({{{\textsf {\textit{A}}}}}\) controlled by \(\varTheta \). Formally, for every \(\theta \in \{0,1\}^n\) the corresponding conditional measurement is specified by the POVM \(\{H^\theta {|x\rangle }{\langle x|} H^\theta \}\) with x ranging over \(\{0,1\}^n\). Here, H is the Hadamard matrix, and \(H^\theta {|x\rangle }\) is a short hand for
denotes the BB84 measurement of an n-qubit system \({{{\textsf {\textit{A}}}}}\) controlled by \(\varTheta \). Formally, for every \(\theta \in \{0,1\}^n\) the corresponding conditional measurement is specified by the POVM \(\{H^\theta {|x\rangle }{\langle x|} H^\theta \}\) with x ranging over \(\{0,1\}^n\). Here, H is the Hadamard matrix, and \(H^\theta {|x\rangle }\) is a short hand for  , where \(\{{|0\rangle },{|1\rangle }\}\) is the computational basis of the qubit system
, where \(\{{|0\rangle },{|1\rangle }\}\) is the computational basis of the qubit system  .
.
Trace Distance. We capture the distance between two states \(\rho ,\sigma \in \mathcal{D}(\mathcal {H})\) in terms of their trace distance \(\delta (\rho , \sigma ):= \frac{1}{2}\Vert \rho -\sigma \Vert _1\), where  is the trace norm of an arbitrary operator K. If the states \(\rho _{{{{\textsf {\textit{A}}}}}}\) and \(\rho _{{{{\textsf {\textit{A}}}}}'}\) are clear from context, we may write \(\delta ({{{\textsf {\textit{A}}}}}, {{{\textsf {\textit{A}}}}}')\) instead of \(\delta (\rho _{{{{\textsf {\textit{A}}}}}}, \rho _{{{{\textsf {\textit{A}}}}}'})\). Also, for any cq-state \(\rho _{X{{{\textsf {\textit{E}}}}}}\) in \(\mathcal{D}(\mathcal{X} \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\), we write \(\delta (X, U_\mathcal{X}|{{{\textsf {\textit{E}}}}})\) as a short hand for \(\delta (\rho _{X{{{\textsf {\textit{E}}}}}}, \mu _\mathcal{X} \otimes \rho _{{{\textsf {\textit{E}}}}})\). Obviously, \(\delta (X, U_\mathcal{X}|{{{\textsf {\textit{E}}}}})\) captures how far away X is from uniformly random on \(\mathcal X\) when given the quantum system \({{{\textsf {\textit{E}}}}}\).
is the trace norm of an arbitrary operator K. If the states \(\rho _{{{{\textsf {\textit{A}}}}}}\) and \(\rho _{{{{\textsf {\textit{A}}}}}'}\) are clear from context, we may write \(\delta ({{{\textsf {\textit{A}}}}}, {{{\textsf {\textit{A}}}}}')\) instead of \(\delta (\rho _{{{{\textsf {\textit{A}}}}}}, \rho _{{{{\textsf {\textit{A}}}}}'})\). Also, for any cq-state \(\rho _{X{{{\textsf {\textit{E}}}}}}\) in \(\mathcal{D}(\mathcal{X} \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\), we write \(\delta (X, U_\mathcal{X}|{{{\textsf {\textit{E}}}}})\) as a short hand for \(\delta (\rho _{X{{{\textsf {\textit{E}}}}}}, \mu _\mathcal{X} \otimes \rho _{{{\textsf {\textit{E}}}}})\). Obviously, \(\delta (X, U_\mathcal{X}|{{{\textsf {\textit{E}}}}})\) captures how far away X is from uniformly random on \(\mathcal X\) when given the quantum system \({{{\textsf {\textit{E}}}}}\).
It is well known that the trace distance is monotone under CPTP maps, and it is easy to see that if two cq-states \(\rho _{X{{{\textsf {\textit{E}}}}}}, \sigma _{X{{{\textsf {\textit{E}}}}}} \in \mathcal{D}(\mathcal{X} \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\) coincide on their classical subsystems, meaning that \(\rho _X = \sigma _X\), then \(\delta (\rho _{X{{{\textsf {\textit{E}}}}}}, \sigma _{X{{{\textsf {\textit{E}}}}}})\) decomposes into \(\delta (\rho _{X{{{\textsf {\textit{E}}}}}}, \sigma _{X{{{\textsf {\textit{E}}}}}}) = \sum _x P_X(x) \, \delta (\rho ^x_{{{{\textsf {\textit{E}}}}}}, \sigma ^x_{{{{\textsf {\textit{E}}}}}})\).
2.2 The Guessing Probability
An important concept in the technical analysis of our scheme(s) is the following notion of guessing probability, which is strongly related to the (conditional) min-entropy as introduced by Renner [17], but turns out to be more convenient to work with for our purpose. Let \(\rho _{X{{{\textsf {\textit{E}}}}}} \in \mathcal{D}(\mathcal{X} \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\) be a cq-state.
Definition 1
The guessing probability of X given \({{{\textsf {\textit{E}}}}}\) is
where the maximum is over all measurements \(\mathcal M: \mathcal{D}(\mathcal {H}_{{{\textsf {\textit{E}}}}}) \rightarrow \mathcal{D}(\mathcal{X})\) of \({{{\textsf {\textit{E}}}}}\) with outcome in \(\mathcal X\).Footnote 6
Note that if \(\varLambda \) is an event, then \(\mathrm {Guess}(X|{{{\textsf {\textit{E}}}}},\varLambda )\) is naturally defined by means of applying the above to the “conditional state” \(\rho _{X{{{\textsf {\textit{E}}}}}|\varLambda } \in \mathcal{D}(\mathcal{X} \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\).
We will make use of the following elementary properties of the guessing probability. In all the statements, it is understood that \(\rho _{X{{{\textsf {\textit{E}}}}}} \in \mathcal{D}(\mathcal{X} \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\), respectively \(\rho _{XZ{{{\textsf {\textit{E}}}}}} \in \mathcal{D}(\mathcal{X} \otimes \mathcal{Z} \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\) in Property 2.
Property 1
\(\mathrm {Guess}(X|\mathcal{Q}({{{\textsf {\textit{E}}}}})) \le \mathrm {Guess}(X|{{{\textsf {\textit{E}}}}})\) for any CPTP map \(\mathcal Q\) acting on \({{{\textsf {\textit{E}}}}}\).
Property 2
\(\mathrm {Guess}(X|Z {{{\textsf {\textit{E}}}}}) = \sum _z P_Z(z) \, \mathrm {Guess}(X|{{{\textsf {\textit{E}}}}},Z\!=\!z)\).
Property 3
\(\mathrm {Guess}(X|{{{\textsf {\textit{E}}}}},\varLambda ) \le \mathrm {Guess}(X|{{{\textsf {\textit{E}}}}})/P[\varLambda ]\) for any event \(\varLambda \).
Note that Property 2 implies that \(\mathrm {Guess}(X|{{{\textsf {\textit{E}}}}},\varLambda ) \le \mathrm {Guess}(X|1_\varLambda {{{\textsf {\textit{E}}}}})/P[\varLambda ]\), but the statement of Property 3 is stronger since \(\mathrm {Guess}(X|{{{\textsf {\textit{E}}}}}) \le \mathrm {Guess}(X|1_\varLambda {{{\textsf {\textit{E}}}}})\).
Proof
(of Property 3 ). It holds thatFootnote 7 \(P[\varLambda ] \cdot \rho _{X {{{\textsf {\textit{E}}}}}|\varLambda } \le \rho _{X {{{\textsf {\textit{E}}}}}}\), and hence that for any measurement \(\mathcal{M}\) on \({{{\textsf {\textit{E}}}}}\)
which implies the claim. \(\square \)
Property 4
There exists \(\sigma _{{{\textsf {\textit{E}}}}}\in \mathcal{D}(\mathcal {H}_{{{\textsf {\textit{E}}}}})\) so that

Proof
The claim follows from Renner’s original definition of the conditional min-entropy as

and the identity \(H_\infty (X|{{{\textsf {\textit{E}}}}}) = -\log \mathrm {Guess}(X|{{{\textsf {\textit{E}}}}})\), as shown in [12]. \(\square \)
3 Enabling Tools
In this section, we introduce and discuss the main technical tools for the constructions and analyses of our key-recycling authentication and encryption schemes.
3.1 On Guessing the Outcome of Quantum Measurements
We consider different “guessing games”, where one or two players need to guess the outcome of a quantum measurement. The bounds are derived by means of the techniques of [19].
Two-player guessing. Here, we consider a game where two parties, Bob and Charlie, need to simultaneously and without communication guess the outcome of BB84 measurements performed by Alice (on n qubits prepared by Bob and Charlie), when given the bases that Alice chose. This is very similar to the monogamy game introduced and studied in [19], but in the version we consider here, the sequence of bases is not chosen from \(\{0,1\}^n\) but from a code \(\mathcal{C}\subset \{0,1\}^n\) with minimal distance d. It is useful to think of d to be much larger than \(\log |\mathcal{C}|\), i.e., the dimension of the code in case of a linear code. The following shows that in case of a uniformly random choice of the bases in \(\mathcal{C}\), Bob and Charlie cannot do much better than to agree on a guess for the bases and to give Alice qubits in those bases.
Proposition 1
Let \(\mathcal {H}_{{{\textsf {\textit{A}}}}}\) be a n-qubit system, and let \(\mathcal {H}_{{{\textsf {\textit{B}}}}}\) and \(\mathcal {H}_{{{\textsf {\textit{C}}}}}\) be arbitrary quantum systems. Consider a state \(\rho _{\varTheta {{{\textsf {\textit{A}}}}}{{{\textsf {\textit{B}}}}}{{{\textsf {\textit{C}}}}}} = \mu _{\mathcal{C}} \otimes \rho _{{{{\textsf {\textit{A}}}}}{{{\textsf {\textit{B}}}}}{{{\textsf {\textit{C}}}}}} \in \mathcal{D}(\mathcal{C}\otimes \mathcal {H}_{{{\textsf {\textit{A}}}}}\otimes \mathcal {H}_{{{\textsf {\textit{B}}}}}\otimes \mathcal {H}_{{{\textsf {\textit{C}}}}})\), and let

where  is the BB84-measurement of the system \({{{\textsf {\textit{A}}}}}\) (controlled by \(\varTheta \)), and \(\mathcal{N}_{\varTheta {{{\textsf {\textit{B}}}}}\rightarrow X'}\) and \(\mathcal{N}_{\varTheta {{{\textsf {\textit{C}}}}}\rightarrow X''}\) are arbitrary (possibly different) measurements of the respective systems \({{{\textsf {\textit{B}}}}}\) and \({{{\textsf {\textit{C}}}}}\), both controlled by \(\varTheta \). Then, it holds that
is the BB84-measurement of the system \({{{\textsf {\textit{A}}}}}\) (controlled by \(\varTheta \)), and \(\mathcal{N}_{\varTheta {{{\textsf {\textit{B}}}}}\rightarrow X'}\) and \(\mathcal{N}_{\varTheta {{{\textsf {\textit{C}}}}}\rightarrow X''}\) are arbitrary (possibly different) measurements of the respective systems \({{{\textsf {\textit{B}}}}}\) and \({{{\textsf {\textit{C}}}}}\), both controlled by \(\varTheta \). Then, it holds that
Proof
The proof uses the techniques from [19]. By Naimark’s theorem, we may assume without loss of generality that the conditional measurements \(\mathcal{N}_{{{{\textsf {\textit{B}}}}}\rightarrow X'}^\theta \) and \(\mathcal{N}_{{{{\textsf {\textit{C}}}}}\rightarrow X''}^\theta \) are specified by families \(\{P_x^{\theta }\}_{x}\) and \(\{Q_x^{\theta }\}_x\) of projections. Then, defining for every \(\theta \in \mathcal{C}\) the projection \(\varPi ^\theta = \sum _x H^\theta {|x\rangle }{\langle x|}H^\theta \otimes P^\theta _x \otimes Q^\theta _x\), we see that
where \(\Vert \cdot \Vert \) refers to the standard operator norm, and the second inequality is by Lemma 2.2 in [19]. For any \(\theta ,\theta ' \in \mathcal{C}\), bounding \(\varPi ^\theta \) and \(\varPi ^{\theta '}\) by

and

it is shown in [19] (in the proof of Theorem 3.4) that
where the last inequality holds unless \(\theta = \theta '\), from which the claim follows. \(\square \)
Remark 1
If we restrict \(\mathcal {H}_{{{\textsf {\textit{B}}}}}\) to be a n-qubit system too, and replace the (arbitrary) measurement \(\mathcal{N}_{\varTheta {{{\textsf {\textit{B}}}}}}\) by a BB84 measurement  , i.e., “Bob measures correctly”, then we get
, i.e., “Bob measures correctly”, then we get
Two-player guessing with quantum side information. Now, we consider a version of the game where Alice’s choice for the bases is not uniformly random, and, additionally, Bob and Charlie may hold some quantum side information on Alice’s choice at the time when they can prepare the initial state (for Alice, Bob and Charlie).
Corollary 1
Let \(\mathcal {H}_{{{\textsf {\textit{A}}}}}\) be a n-qubit system, and let \(\mathcal {H}_{{{\textsf {\textit{B}}}}}, \mathcal {H}_{{{\textsf {\textit{C}}}}}\) and \(\mathcal {H}_{{{\textsf {\textit{E}}}}}\) be arbitrary quantum systems. Consider a state \(\rho _{\varTheta {{{\textsf {\textit{E}}}}}} \in \mathcal{D}(\mathcal{C}\otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\), and let
where \(\mathcal{Q}_{{{{\textsf {\textit{E}}}}}\rightarrow {{{\textsf {\textit{A}}}}}{{{\textsf {\textit{B}}}}}{{{\textsf {\textit{C}}}}}}\) is a CPTP map acting on \({{{\textsf {\textit{E}}}}}\) (only), and let

as in Proposition 1 above. Then, it holds that
Proof
By Proposition 1, the claim holds as \(P[X' \!=\! X \wedge X'' \!=\! X] \le 1/|\mathcal{C}| + 1/2^{d/2}\) for the special case where \(\rho _{\varTheta {{{\textsf {\textit{E}}}}}}\) is of the form \(\rho _{\varTheta {{{\textsf {\textit{E}}}}}} = \mu _\mathcal{C}\otimes \sigma _{{{\textsf {\textit{E}}}}}\). Furthermore, by Property 4 we know that an arbitrary \(\rho _{\varTheta {{{\textsf {\textit{E}}}}}}\in \mathcal{D}(\mathcal{C}\otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\) is bounded by
Therefore, since the composed map

is still a CPTP map, it holds that for arbitrary \(\rho _{\varTheta {{{\textsf {\textit{E}}}}}} \in \mathcal{D}(\mathcal{C}\otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\)
which proves the claim. \(\square \)
Remark 2
Similarly to the remark above, the bound relaxes to
when “Bob measure correctly”.
Single-player guessing (with quantum side information). Corollary 1 immediately gives us control also over a slightly different game, where only one party needs to guess Alice’s measurement outcome, but here he is not given the bases. Indeed, any strategy here gives a strategy for the above simultaneous-guessing game, simply by “pre-measuring” \({{{\textsf {\textit{B}}}}}\), and having Bob and Charlie each keep a copy of the measurement outcome.
Corollary 2
Let \(\mathcal {H}_{{{\textsf {\textit{A}}}}}\) be a n-qubit system, and let \(\mathcal {H}_{{{\textsf {\textit{B}}}}}\) and \(\mathcal {H}_{{{\textsf {\textit{E}}}}}\) be arbitrary quantum systems. Consider a state \(\rho _{\varTheta {{{\textsf {\textit{E}}}}}} \in \mathcal{D}(\mathcal{C}\otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\) and let
where \(\mathcal{Q}_{{{{\textsf {\textit{E}}}}}\rightarrow {{{\textsf {\textit{A}}}}}{{{\textsf {\textit{B}}}}}}\) is a CPTP map acting on \({{{\textsf {\textit{E}}}}}\), and let

where \(\mathcal{N}_{{{{\textsf {\textit{B}}}}}\rightarrow X''}\) is an arbitrary measurement of \({{{\textsf {\textit{B}}}}}\) (with no access to \(\varTheta \)). Then, it holds that
In other words, for the state  we have that
we have that
Remark 3
If we restrict the side information \({{{\textsf {\textit{E}}}}}\) to be classical then, using slightly different techniques, we can improve the bounds from Corollaries 1 and 2 to
Whether this improved bound also holds in case of quantum side information is an open question.
3.2 Hash Functions with Message-Independence and Key-Privacy
The goal of key-recycling is to be able to re-use a cryptographic key. For this to be possible, it is necessary — actually, not necessary but sufficient — that a key stays secure, i.e., that the primitive that uses the key does not reveal anything on the key, or only very little. We introduce here a general notion that captures this, i.e., that ensures that the key stays secure as long as there is enough uncertainty in the message the primitive is applied to — in our construction(s), this uncertainty will then be derived from the quantum part.
Consider a keyed hash function \(\mathsf{H}: \mathcal{K}\times \mathcal{X} \rightarrow \mathcal{Y}\) with key space \(\mathcal{K}\), message space \(\mathcal X\), and range \(\mathcal Y\). We define the following properties on such a hash function.
Definition 2
We say that \(\mathsf{H}\) is message-independent if for a uniformly random key K in \(\mathcal{K}\), the distribution of the hash value \(Y = \mathsf{H}(K,x)\) is independent of the message \(x \in \mathcal X\). And, we say that \(\mathsf{H}\) is uniform if it is message-independent and \(Y = \mathsf{H}(K,x)\) is uniformly random on \(\mathcal Y\).
Thus, message-independence simply ensures that if the key is uniformly random and independent of the message, then the hash of the message is independent of the message too. The key-privacy property below on the other hand ensures that for any adversary that has arbitrary but limited information on the message and the hash value — but no direct information on the key — has (almost) no information on the key.
Definition 3
We say that \(\mathsf{H}\) offers \(\nu \) -key-privacy if for any state \(\rho _{KXY{{{\textsf {\textit{E}}}}}}\) in \(\mathcal{D}(\mathcal{K}\otimes \mathcal{X} \otimes \mathcal{Y} \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\) with the properties that \(\rho _{KX} = \mu _\mathcal{K}\otimes \rho _X\), \(Y = \mathsf{H}(K,X)\) and \(K\leftrightarrow XY\leftrightarrow {{{\textsf {\textit{E}}}}}\), it holds that
We say that \(\mathsf{H}\) offers ideal key-privacy if it offers 1-key-privacy.
Remark 4
Note that if \(\mathsf{H}\) is message-independent then for X, Y and \({{{\textsf {\textit{E}}}}}\) as above in Definition 3, we have that \(\mathrm {Guess}(X|Y{{{\textsf {\textit{E}}}}}) = \mathrm {Guess}(X|{{{\textsf {\textit{E}}}}})\).
Not so surprisingly, the joint notion of uniformity and key-privacy is closely related to that of a strong extractor [14]. Indeed, if \(\mathsf{H}\) is uniform and offers key-privacy then it is a strong extractor: for \(\rho _{KXE} = \mu _\mathcal{K}\otimes \rho _{XE}\) and \(Y = \mathsf{H}(K,X)\), the condition on \(\rho _{KXY{{{\textsf {\textit{E}}}}}}\) in Definition 3 is satisfied, and thus we have the promised bound on \(\delta (\rho _{KY{{{\textsf {\textit{E}}}}}},\mu _\mathcal{K}\otimes \rho _{Y{{{\textsf {\textit{E}}}}}}) = \delta (\rho _{KY{{{\textsf {\textit{E}}}}}},\mu _\mathcal{K}\otimes \mu _\mathcal{Y} \otimes \rho _{{{\textsf {\textit{E}}}}})\), where the equality is due to uniformity. As such, [18] shows that the required bound on \(\delta (K,U_\mathcal{K}|Y{{{\textsf {\textit{E}}}}})\) is the best one can hope for. On the other hand, the following shows that from every strong extractor we can easily construct a hash function that offers uniformity and key-privacy.
Proposition 2
Let \(\mathsf{Ext}: \mathcal{K}\times \mathcal{X} \rightarrow \mathcal{Y}\) be a strong extractor, meaning that for \(\rho _{K X {{{\textsf {\textit{E}}}}}} = \mu _\mathcal{K}\otimes \rho _{X {{{\textsf {\textit{E}}}}}} \in \mathcal{D}(\mathcal{K}\otimes \mathcal{X} \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\) and for Y computed as \(Y = \mathsf{Ext}(K,X)\) it holds that \(\delta (\rho _{KY{{{\textsf {\textit{E}}}}}},\mu _\mathcal{K}\otimes \rho _{Y{{{\textsf {\textit{E}}}}}}) \le \frac{\nu }{2} \sqrt{\mathrm {Guess}(X|{{{\textsf {\textit{E}}}}})\cdot |\mathcal{Y}|}\). Furthermore, we assume that the range \(\mathcal Y\) forms a group. Then, the keyed hash functionFootnote 8

with key space \(\mathcal{K}\times \mathcal{Y}\) satisfies uniformity and \(\nu \)-key-privacy.
Proof
Uniformity is clear. For key-privacy, consider a state \(\rho _{KXY{{{\textsf {\textit{E}}}}}}\) with the properties as in Definition 3. We fix an arbitrary \(y \in \mathcal Y\) and condition on \(Y = y\). Conditioning on \(X = x\) as well for an arbitrary \(x \in \mathcal X\), the key \((K,K')\) is uniformly distributed subject to \(\mathsf{H}(K,x)+K' = y\). In other words, K is uniformly random in \(\mathcal{K}\), and \(K' = y - \mathsf{H}(K,x)\). Therefore, making use of the Markov-chain property, conditioning on \(Y = y\) only, K is uniformly random in \(\mathcal{K}\) and independent of X and \({{{\textsf {\textit{E}}}}}\), and \(K' = y - \mathsf{H}(K,X)\). Thus, by the extractor property, \(\delta (\rho _{K'K{{{\textsf {\textit{E}}}}}|Y=y},\mu _\mathcal{Y} \otimes \mu _\mathcal{K}\otimes \rho _{{{{\textsf {\textit{E}}}}}|Y=y}) \le \frac{\nu }{2} \sqrt{\mathrm {Guess}(X|{{{\textsf {\textit{E}}}}},Y\!=\!y)\cdot |\mathcal{Y}|}\). The claim follows by averaging over y, and applying Jensen’s inequality and Property 2. \(\square \)
The following technical result will be useful.
Lemma 1
Let \(\mathsf{H}: \mathcal{K}\times \mathcal{X} \rightarrow \mathcal{Y}\) be a keyed hash function that satisfies message-independence. Furthermore, let \(\rho _{KXY{{{\textsf {\textit{E}}}}}}\) be a state with the properties as in Definition 3. Then
Proof
Note that the Markov-chain property \(K\leftrightarrow XY\leftrightarrow {{{\textsf {\textit{E}}}}}\) can be understood in that \({{{\textsf {\textit{E}}}}}\) is obtained by acting on XY only: \({{{\textsf {\textit{E}}}}}= \mathcal{Q}(X Y)\). For the purpose of the argument, we extend the state \(\rho _{X K Y {{{\textsf {\textit{E}}}}}}\) to a state \(\rho _{X K K' Y Y' {{{\textsf {\textit{E}}}}}{{{\textsf {\textit{E}}}}}'}\) as follows. We choose a uniformly random and independent \(K'\) in \(\mathcal{K}\), and set \(Y' = \mathsf{H}(K',X)\) and \({{{\textsf {\textit{E}}}}}' = \mathcal{Q}(X Y')\). Note that \(\rho _{X K Y {{{\textsf {\textit{E}}}}}}\) coincides with \(\rho _{X K' Y' {{{\textsf {\textit{E}}}}}'}\). Therefore,
where the second equality is by the independence of K. Furthermore, by Property 3, we have that
Finally, by the message-independence of \(\mathsf{H}\), it holds that \(Y'\) is independent of \(K X Y {{{\textsf {\textit{E}}}}}\) (and with the same distribution as Y), and therefore \(P[Y \!=\! Y'] \ge 1/|\mathcal{Y}|\) and \(\mathrm {Guess}(X|K Y {{{\textsf {\textit{E}}}}},Y \!=\! Y') = \mathrm {Guess}(X|K Y {{{\textsf {\textit{E}}}}})\). Altogether, this gives us the bound \(\mathrm {Guess}(X|K Y {{{\textsf {\textit{E}}}}}) \le \mathrm {Guess}(X| Y {{{\textsf {\textit{E}}}}}) \cdot |\mathcal{Y}|\), which concludes the proof. \(\square \)
Equipped with Lemma 1, we can now show the following composition results.
Proposition 3
(Parallel Composition). Consider two keyed hash functions \(\mathsf{H}_1: \mathcal{K}_1 \times \mathcal{X} \rightarrow \mathcal{Y}_1\) and \(\mathsf{H}_2: \mathcal{K}_2 \times \mathcal{X} \rightarrow \mathcal{Y}_2\) with the same message space \(\mathcal X\), and

with key space \(\mathcal{K}= \mathcal{K}_1 \times \mathcal{K}_2\) and range \(\mathcal{Y} = \mathcal{Y}_1 \times \mathcal{Y}_2\). If \(\mathsf{H}_1\) and \(\mathsf{H}_2\) are both message-independent (or uniform) and respectively offer \(\nu _1\)- and \(\nu _2\)-key privacy, then \(\mathsf{H}\) is message-independent (or uniform) and offers \((\nu _1+\nu _2)\)-key privacy.
Proof
That message-independence/uniformity is preserved is clear. To argue key-privacy, assume that we have \(\rho _{K_1 K_2 X} = \rho _{K_1} \otimes \rho _{K_2} \otimes \rho _X\), \(Y_1 = \mathsf{H}_1(K_1,X)\) and \(Y_2 = \mathsf{H}(K_2,X)\), and \(K_1 K_2\leftrightarrow XY_1 Y_2\leftrightarrow {{{\textsf {\textit{E}}}}}\). We need to bound the distance of \(K_1 K_2\) from uniform when given \(Y_1 Y_1{{{\textsf {\textit{E}}}}}\), which we can decompose into
The above conditions on \(\rho _{K_1 K_2 X Y_1 Y_2 {{{\textsf {\textit{E}}}}}}\) imply that \(K_1 \leftrightarrow XY_1 \leftrightarrow K_2 Y_2 {{{\textsf {\textit{E}}}}}\) holds, and thus also \(K_1 \leftrightarrow XY_1 \leftrightarrow Y_2 {{{\textsf {\textit{E}}}}}\). Indeed, \(K_1 K_2\leftrightarrow XY_1 Y_2\leftrightarrow {{{\textsf {\textit{E}}}}}\) implies that also \(K_1 \leftrightarrow XY_1 K_2 Y_2\leftrightarrow {{{\textsf {\textit{E}}}}}\), which together with \(K_1 \leftrightarrow XY_1 \leftrightarrow K_2 Y_2\) (which holds by choice of \(K_2\) and \(Y_2\)) implies that \(K_1 \leftrightarrow XY_1 \leftrightarrow K_2 Y_2 {{{\textsf {\textit{E}}}}}\). Therefore, by the key-privacy property of \(\mathsf{H}_1\), setting \({{{\textsf {\textit{E}}}}}_1 = Y_2 {{{\textsf {\textit{E}}}}}\), we see that
Similarly, \(K_2 \leftrightarrow XY_2 \leftrightarrow K_1 Y_1 {{{\textsf {\textit{E}}}}}\), and so by the key-privacy property of \(\mathsf{H}_2\), setting \({{{\textsf {\textit{E}}}}}_2 = K_1 Y_1 {{{\textsf {\textit{E}}}}}\), we conclude that
which proves the claim. \(\square \)
Proposition 4
(“Sequarallel” Composition). Consider two keyed hash functions \(\mathsf{H}_1: \mathcal{K}_1 \times \mathcal{X} \rightarrow \mathcal{Y}_1\) and \(\mathsf{H}_2: \mathcal{K}_2 \times (\mathcal{X}\otimes \mathcal{Y}_1) \rightarrow \mathcal{Y}_2\) with message spaces as specified, and

with key space \(\mathcal{K}= \mathcal{K}_1 \times \mathcal{K}_2\) and range \(\mathcal{Y} = \mathcal{Y}_1 \times \mathcal{Y}_2\). If \(\mathsf{H}_1\) and \(\mathsf{H}_2\) are both message-independent (or uniform) and respectively offer \(\nu _1\)- and \(\nu _2\)-key privacy, then \(\mathsf{H}\) is message-independent (or uniform) and offers \((\nu _1+\nu _2)\)-key privacy.
Proof
The proof goes along the same lines as the proof of Proposition 3, except that in the reasoning for the bound on \(\delta (K_2,U_{\mathcal{K}_2}| K_1 Y_1 {{{\textsf {\textit{E}}}}})\), we append \(Y_1\) to X, with the consequence that we get a bound that is in terms of \(\mathrm {Guess}(X Y_1|Y_2 Y_1 {{{\textsf {\textit{E}}}}})\), but this obviously coincides with \(\mathrm {Guess}(X|Y_2 Y_1 {{{\textsf {\textit{E}}}}})\), and thus we end up with the same bound. \(\square \)
4 Message Authentication with Key-Recycling
We first consider the problem of message authentication with key-recycling. It turns out that — at least with our approach — this is the actual challenging problem, and extending to (authenticated) encryption is then quite easy.
4.1 The Semantics
We quickly specify the semantics of a quantum authentication code (or scheme) with key-recycling.Footnote 9
Definition 4
A quantum authentication code (with key recycling) \(\mathsf{QMAC}\) with message space \(\mathcal{MSG}\) and key space \(\mathcal{KEY}\) is made up of the following components: (1) A CPTP map \(\mathsf{Auth}\) that is controlled by a message \(msg\in \mathcal{MSG}\) and a key \(key\in \mathcal{KEY}\), and that acts on an empty system and outputs a quantum authentication tag (with a fixed state space), (2) a measurement \(\mathsf{Verify}\) that is controlled by \(msg\in \mathcal{MSG}\) and \(key\in \mathcal{KEY}\), and that acts on a quantum authentication tag and outputs a decision bit \(d \in \{0,1\}\), and (3) a randomized function \(\mathsf{Refresh}: \mathcal{KEY}\rightarrow \mathcal{KEY}\).
We will often identify an authentication code, formalized as above, with the obvious authenticated-message-transmission protocol \(\pi _{\mathsf{QMAC}}(msg)\), where Alice and Bob start with a shared key \(key\in \mathcal{KEY}\), and Alice sends the message \(msg\) along with its quantum authentication tag prepared by means of \(\mathsf{Auth}\) to Bob over a channel that is controlled by the adversary Eve, and, upon reception of the (possibly modified) message and tag, Bob verifies correctness using \(\mathsf{Verify}\) and accordingly accepts or rejects. If he rejects, then Alice and Bob replace \(key\) by \(key' := \mathsf{Refresh}(key)\).Footnote 10 Note that, for any message \(msg\in \mathcal{MSG}\) and any strategy for Eve on how to interfere with the communication, the protocol \(\pi _{\mathsf{QMAC}}(msg)\) induces a CPTP map \(\mathcal{E}{ xe}[\pi _{\mathsf{QMAC}}(msg)]: \mathcal{D}(\mathcal{KEY}\otimes \mathcal {H}_{{{\textsf {\textit{E}}}}}) \rightarrow \mathcal{D}(\mathcal{KEY}\otimes \mathcal {H}_{{{{\textsf {\textit{E}}}}}'})\) that describes the evolution of the shared key \(key\) and Eve’s local system as a result of the execution of \(\pi _{\mathsf{QMAC}}(msg)\).
Our goal will be to show that, for our construction given below, and for any behavior of Eve, the CPTP map \(\mathcal{E}{ xe}[\pi _{\mathsf{QMAC}}(msg)]\) maps a key about which Eve has little information into a (possibly updated) key about which Eve still has little information — what it means here to “have little information” needs to be specified, but it will in particular imply that it still allows Bob to detect a modification of the message. This then ensures re-usability of the quantum authentication code — with the same key as long as Bob accepts the incoming messages, and with the updated key in case he rejects.
4.2 The Scheme
Let \(\mathcal{MSG}\) be an arbitrary non-empty finite set. We are going to construct a quantum message authentication code \(\mathsf{QMAC}\) with message space \(\mathcal{MSG}\). To this end, let \(\mathsf{MAC}: \mathcal{K}\times (\mathcal{MSG}\times \{0,1\}^n) \rightarrow \mathcal{T}\) be a classical one-time message authentication code with a message space \(\mathcal{MSG}\times \{0,1\}^n\) for some  . We require \(\mathsf{MAC}\) to be secure in the standard sense, meaning a modified message will be detected except with small probability \(\varepsilon _\mathsf{MAC}\). Additionally, we require \(\mathsf{MAC}\) to satisfy message-independence and ideal key-privacy, as discussed in Sect. 3.2. Actually, it is sufficient if \(\mathsf{MAC}(\,\cdot \,,msg\Vert \,\cdot \,)\), i.e., the hash function \(\mathcal{K}\times \{0,1\}^n \rightarrow \mathcal{T}\),
. We require \(\mathsf{MAC}\) to be secure in the standard sense, meaning a modified message will be detected except with small probability \(\varepsilon _\mathsf{MAC}\). Additionally, we require \(\mathsf{MAC}\) to satisfy message-independence and ideal key-privacy, as discussed in Sect. 3.2. Actually, it is sufficient if \(\mathsf{MAC}(\,\cdot \,,msg\Vert \,\cdot \,)\), i.e., the hash function \(\mathcal{K}\times \{0,1\}^n \rightarrow \mathcal{T}\),  obtained by fixing \(msg\), satisfies message-independence and ideal key-privacy for any \(msg\in \mathcal{MSG}\). Assuming that \(\mathcal{MSG}\) consists of bit strings of fixed size so that \(\mathcal{MSG}\times \{0,1\}^n = \{0,1\}^N\) for some
obtained by fixing \(msg\), satisfies message-independence and ideal key-privacy for any \(msg\in \mathcal{MSG}\). Assuming that \(\mathcal{MSG}\) consists of bit strings of fixed size so that \(\mathcal{MSG}\times \{0,1\}^n = \{0,1\}^N\) for some  , the canonical message authentication codes
, the canonical message authentication codes  ,
,  and
and  ,
,  , where
, where  is an arbitrary surjective
is an arbitrary surjective  -linear map, are suitable choices; this follows directly from Proposition 2. Finally, let \(\mathcal{C}\subset \{0,1\}^n\) be a code with large minimal distance d.
-linear map, are suitable choices; this follows directly from Proposition 2. Finally, let \(\mathcal{C}\subset \{0,1\}^n\) be a code with large minimal distance d.
Then, our quantum message authentication code \(\mathsf{QMAC}\) has a key space \(\mathcal{KEY}= \mathcal{K}\times \mathcal{C}\), where for a key \(k \Vert \theta \in \mathcal{K}\times \mathcal{C}\) we refer to k as the “MAC key” and to \(\theta \) as the “basis key”, and \(\mathsf{QMAC}\) works as described in Fig. 1.
It is clear that as long as the MAC key k is “secure enough”, the classical \(\mathsf{MAC}\) takes care of an Eve that tries to modify the message \(msg\), and it ensures that such an attack is detected by Bob, except with small probability. What is non-trivial to argue is that the MAC key (together with the basis key) indeed stays “secure enough” over multiple executions of \(\pi _\mathsf{QMAC}(msg)\); this is what we show below.
4.3 Analysis
We consider an execution of the authenticated-message-transmission protocol \(\pi _\mathsf{QMAC}(msg)\) for a fixed message \(msg\). Let \(\rho _{K \varTheta {{{\textsf {\textit{E}}}}}} \in \mathcal{D}(\mathcal{K}\otimes \mathcal{C}\otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\) be the joint state before the execution, consisting of the MAC key K, the basis key \(\varTheta \), and Eve’s local quantum system \({{{\textsf {\textit{E}}}}}\). The joint state \(\mathcal{E}{ xe}[\pi _{\mathsf{QMAC}}(msg)](\rho _{K\varTheta {{{\textsf {\textit{E}}}}}})\) after the execution is given by \(\rho _{K \varTheta ' T D {{{\textsf {\textit{C}}}}}} \in \mathcal{D}(\mathcal{K}\otimes \mathcal{C}\otimes \mathcal{T}\otimes \{0,1\} \otimes \mathcal {H}_{{{\textsf {\textit{C}}}}})\), where \(\varTheta '\) is the (possibly) updated basis key, T is the classical tag, D is Bob’s decision to accept or reject, and \({{{\textsf {\textit{C}}}}}\) is Eve’s new quantum system. Eve’s complete information after the execution of the scheme is thus given by \({{{\textsf {\textit{E}}}}}' = T D {{{\textsf {\textit{C}}}}}\).
Recall that \(T D {{{\textsf {\textit{C}}}}}\) is obtained as follows from \(K \varTheta {{{\textsf {\textit{E}}}}}\). Alice prepares BB84-qubits \({{{\textsf {\textit{B}}}}}_\circ \) for uniformly random bits X and with bases determined by \(\varTheta \), and she computes the tag \(T := \mathsf{MAC}(K,msg\Vert X)\). Then, Eve acts on \({{{\textsf {\textit{B}}}}}_\circ {{{\textsf {\textit{E}}}}}\) (in a way that may depend on T) and keeps one part, \({{{\textsf {\textit{C}}}}}\), of the resulting state, and Bob measures the other part, \({{{\textsf {\textit{B}}}}}\), to obtain \(X'\) and checks with the (possibly modified) tag T to decide on D.
Note that by a standard reasoning, we can think of the BB84 qubits \({{{\textsf {\textit{B}}}}}_\circ \) not as being prepared by first choosing the classical bits X and then “encoding" them into qubits with the prescribed bases \(\varTheta \), but by first preparing n EPR pairs \(\varPhi ^+_{{{{\textsf {\textit{A}}}}}{{{\textsf {\textit{B}}}}}_\circ }\) and then measuring the qubits in \({{{\textsf {\textit{A}}}}}\) in the prescribed bases to obtain X, i.e.,  .
.
The following captures the main security property of the scheme.
Theorem 1
If the state before the execution of \(\pi _\mathsf{QMAC}(msg)\) is of the form \(\rho _{K\varTheta {{{\textsf {\textit{E}}}}}} = \mu _\mathcal{K}\otimes \rho _{\varTheta {{{\textsf {\textit{E}}}}}}\), then for any Eve the state \(\rho _{K \varTheta ' {{{\textsf {\textit{E}}}}}'} = \mathcal{E}{ xe}[\pi _{\mathsf{QMAC}}(msg)](\rho _{K\varTheta {{{\textsf {\textit{E}}}}}})\) after the execution satisfies
and
This means that if before the execution of \(\pi _\mathsf{QMAC}(msg)\), it holds that Eve’s guessing probability on \(\varTheta \) is small and K looks perfectly random to her (even when given \(\varTheta \)), then after the execution, Eve’s guessing probability on (the possibly refreshed) \(\varTheta '\) is still small and K still looks almost perfectly random to her. As such, we may then consider a hypothetical refreshing of K that has almost no impact, but which brings us back to the position to apply Theorem 1 again, and hence allows us to re-apply this “preservation of security” for the next execution, and so on. This in particular allows us to conclude that in an arbitrary sequence of executions, the MAC key K stays almost perfectly random for Eve, and thus any tampering with an authenticated message will be detected by Bob except with small probability by the security of \(\mathsf{MAC}\) (see Sect. 4.4 for more details).
Remark 5
For simplicity, in Theorem 1 and in the remainder of this work, we assume the message \(msg\) to be arbitrary but fixed. However, it is not hard to see that we may also allow \(msg\) to be obtained by means of a measurement, applied to Eve’s system \({{{\textsf {\textit{E}}}}}\) before the execution of \(\pi _\mathsf{QMAC}(msg)\), i.e., Eve can choose it. The bounds of Theorem 1 then hold on average over the measured \(msg\). This follows directly from Property 2 for the bound the guessing probability, and from a similar decomposition property for the trace distance, together with Jensen’s inequality for the bound on the trace distance. We emphasize however, that we do assume \(msg\), even when provided by Eve, to be classical, i.e., we do not consider so-called superposition attacks.
The formal proof of Theorem 1 is given below; the intuition is as follows. For the bound on the guessing probability of the (possibly updated) basis key, we have that in case Bob rejects and so the basis key is re-sampled from \(\mathcal{C}\), Eve has obviously guessing probability \(1/|\mathcal{C}|\). In case Bob accepts, the fact that Bob accepts may increase Eve’s guessing probability. For instance, Eve may measure one qubit in, say, the computational basis, and forward the correspondingly collapsed qubit to Bob; if Bob then accepts it is more likely that this qubit had been prepared in the computational basis by Alice, giving Eve some (new) information on the basis key. However, the resulting increase in guessing probability is inverse proportional to the probability that Bob actually accepts, so that this advantage is “canceled out” by the possibility that Bob will not accept. For the bound on the “freshness” of K (given the basis key \(\varTheta '\)), by key privacy it is sufficient to argue that Eve has small guessing probability for X. In case Bob rejects, the (refreshed) basis key is useless to her for guessing X, and so the task of guessing X reduces to winning the game considered in Corollary 2. Similarly, the case where Bob accepts fits into the game in Corollary 1. In both cases, we get that the guessing probability of X essentially coincides with \(\mathrm {Guess}(\varTheta |{{{\textsf {\textit{E}}}}})\).
Proof
For the first claim, we simply observe that
where the second equality holds because \(\varTheta '\) is freshly chosen in case Bob rejects and \(\varTheta ' = \varTheta \) in case he accepts, and the final equality holds because of the fact that  .
.
For the second claim, consider \(\tilde{D}\) and \(\tilde{\varTheta }'\) as follows. \(\tilde{D}\) is 1 if \(X=X'\) and Eve has not modified the tag T nor the message \(msg\), and \(\tilde{D}\) is 0 otherwise (i.e., \(\tilde{D}\) is an “ideal version” of Bob’s decision), and \(\tilde{\varTheta }'\) is freshly chosen if and only \(\tilde{D} = 0\). The states of \(K\varTheta 'TD {{{\textsf {\textit{C}}}}}\) and \(K\tilde{\varTheta }'T\tilde{D} {{{\textsf {\textit{C}}}}}\) are identical except for when \(D = 1\) but \(X \ne X'\) or Eve has modified T or \(msg\), which happens with probability at most \(\varepsilon _\mathsf{MAC}\) by the security of \(\mathsf{MAC}\), and thus the two states are \(\varepsilon _\mathsf{MAC}\)-close. Therefore, \(\delta (K, U_\mathcal{K}|\varTheta 'T D {{{\textsf {\textit{C}}}}}) \le \delta (K, U_\mathcal{K}|\tilde{\varTheta }'T\tilde{D} {{{\textsf {\textit{C}}}}}) + 2 \varepsilon _\mathsf{MAC}\), and so it suffices to analyze the state of \(K\tilde{\varTheta }'T\tilde{D} {{{\textsf {\textit{C}}}}}\). Furthermore, we may assume that Eve’s state \({{{\textsf {\textit{C}}}}}\) contains the information of whether she modified T or \(msg\), so that \(\tilde{D}\) can be computed from \(1_{X=X'}\) when given \({{{\textsf {\textit{C}}}}}\), and thus \(\delta (K,U_\mathcal{K}|\tilde{\varTheta }'\tilde{D} T {{{\textsf {\textit{C}}}}}) \le \delta (K,U_\mathcal{K}|\tilde{\varTheta }'\,1_{X=X'} \tilde{D} T {{{\textsf {\textit{C}}}}}) = \delta (K,U_\mathcal{K}|\tilde{\varTheta }'\,1_{X=X'} T {{{\textsf {\textit{C}}}}})\).
Now, since K is random and independent of \(X \varTheta {{{\textsf {\textit{B}}}}}_\circ {{{\textsf {\textit{E}}}}}\), T is computed as \(T = \mathsf{MAC}(K,msg|X)\), and \(\tilde{\varTheta } \,1_{X=X'} {{{\textsf {\textit{C}}}}}\) is obtained by acting on T and \(X \varTheta {{{\textsf {\textit{B}}}}}_\circ {{{\textsf {\textit{E}}}}}\) only (and not on K), we see that the conditions required in Definition 3 are satisfied. Therefore, by the key-privacy of \(\mathsf{MAC}\), and recalling Remark 4,
Furthermore, by Property 2, and noting that \(\tilde{\varTheta }'\) is freshly chosen when \(X\!\ne \!X'\) and equal to \(\varTheta \) otherwise,
For the first term, we see that

where the final inequality follows from Corollary 2 by recalling that  . Similarly, writing \(X''\) for the measurement outcome when measuring \({{{\textsf {\textit{C}}}}}\) using an optimal measurement \(\mathcal{N}_{\varTheta {{{\textsf {\textit{C}}}}}}\) (controlled by \(\varTheta \)), we obtain
. Similarly, writing \(X''\) for the measurement outcome when measuring \({{{\textsf {\textit{C}}}}}\) using an optimal measurement \(\mathcal{N}_{\varTheta {{{\textsf {\textit{C}}}}}}\) (controlled by \(\varTheta \)), we obtain
where the final inequality follows from Corollary 1 by observing that, using uniformity of \(\mathsf{MAC}\) (Definition 2) in the second equality,

where \(\mathcal{Q}'_{{{{\textsf {\textit{E}}}}}\rightarrow {{{\textsf {\textit{A}}}}}{{{\textsf {\textit{B}}}}}{{{\textsf {\textit{C}}}}}}\) is the CPTP map \(\mathcal{Q}'_{{{{\textsf {\textit{E}}}}}\rightarrow {{{\textsf {\textit{A}}}}}{{{\textsf {\textit{B}}}}}{{{\textsf {\textit{C}}}}}}(\sigma _{{{\textsf {\textit{E}}}}}) = \mathcal{Q}_{T {{{\textsf {\textit{B}}}}}_\circ {{{\textsf {\textit{E}}}}}\rightarrow {{{\textsf {\textit{B}}}}}{{{\textsf {\textit{C}}}}}}(\varPhi ^+_{{{{\textsf {\textit{A}}}}}{{{\textsf {\textit{B}}}}}_\circ } \otimes \sigma _{{{\textsf {\textit{E}}}}}\otimes \rho _T)\). Collecting the terms gives the claimed bound. \(\square \)
4.4 Re-usability of \(\mathsf{QMAC}\)
We formally argue here that Theorem 1, which analyses a single usage of \(\mathsf{QMAC}\), implies re-usability. The reason why this is not completely trivial is that after one execution of \(\pi _\mathsf{QMAC}\), the MAC key K is not perfectly secure anymore but “only” almost-perfectly secure, so that Theorem 1 cannot be directly applied anymore for a second execution. However, taking care of this is quite straightforward.
Formally, we have the following result regarding the re-usability of \(\mathsf{QMAC}\).
Proposition 5
If Alice and Bob start off with a uniformly random key, then for a sequence \(\pi _{\mathsf{QMAC}}(msg_1)\), \(\pi _{\mathsf{QMAC}}(msg_2),\ldots \) of sequential executions of protocol \(\pi _{\mathsf{QMAC}}\), and for any strategy for Eve and any  , the probability \(\varepsilon _i\) that Eve modifies \(msg_{i}\) in the execution of \(\pi _{\mathsf{QMAC}}(msg_{i})\) yet Bob accepts is bounded by
, the probability \(\varepsilon _i\) that Eve modifies \(msg_{i}\) in the execution of \(\pi _{\mathsf{QMAC}}(msg_{i})\) yet Bob accepts is bounded by
Proof
In case \(i = 1\), the statement reduces to \(\varepsilon _i \le \varepsilon _\mathsf{MAC}\), which holds by construction of \(\mathsf{QMAC}\). To argue the general case, let \(\rho _{K_1 \varTheta _1 {{{\textsf {\textit{E}}}}}_1},\rho _{K_2 \varTheta _2 {{{\textsf {\textit{E}}}}}_2},\ldots \) describe the evolution of the MAC key and the basis key and Eve’s information on them, given that we start with a perfect key \(\rho _{K_0 \varTheta _0 {{{\textsf {\textit{E}}}}}_0} = \mu _{\mathcal{K}} \otimes \mu _{\mathcal{C}} \otimes \rho _{{{{\textsf {\textit{E}}}}}_0}\). Formally, \(\rho _{K_i \varTheta _i {{{\textsf {\textit{E}}}}}_i}\) is inductively defined as \(\rho _{K_i \varTheta _i {{{\textsf {\textit{E}}}}}_i} = \mathcal{E}{ xe}[\pi _{\mathsf{QMAC}}(msg_i)](\rho _{K_{i-1} \varTheta _{i-1} {{{\textsf {\textit{E}}}}}_{i-1}})\). For the sake of the argument, we also consider \(\tilde{\rho }_{K_1 \varTheta _1 {{{\textsf {\textit{E}}}}}_1},\tilde{\rho }_{K_2 \varTheta _2 {{{\textsf {\textit{E}}}}}_2},\ldots \) obtained by means of setting \(\tilde{\rho }_{K_0 \varTheta _0 {{{\textsf {\textit{E}}}}}_0} = \rho _{K_0 \varTheta _0 {{{\textsf {\textit{E}}}}}_0}\) and \(\tilde{\rho }_{K_i \varTheta _i {{{\textsf {\textit{E}}}}}_i} = \mathcal{E}{ xe}[\pi _{\mathsf{QMAC}}(msg_i)](\mu _{\mathcal{K}} \otimes \tilde{\rho }_{\varTheta _{i-1} {{{\textsf {\textit{E}}}}}_{i-1}})\), i.e., the evolution of the keys and Eve’s information in a hypothetical setting where the MAC key is refreshed before every new execution. For these latter states \(\tilde{\rho }_{K_i \varTheta _i {{{\textsf {\textit{E}}}}}_i} \), we can inductively apply Theorem 1 and conclude that
and
for any  . But now, for the original states \(\rho _{K_1 \varTheta _1 {{{\textsf {\textit{E}}}}}_1},\rho _{K_2 \varTheta _2 {{{\textsf {\textit{E}}}}}_2},\ldots \), from the triangle inequality we obtain that
. But now, for the original states \(\rho _{K_1 \varTheta _1 {{{\textsf {\textit{E}}}}}_1},\rho _{K_2 \varTheta _2 {{{\textsf {\textit{E}}}}}_2},\ldots \), from the triangle inequality we obtain that
where the last inequality is by induction (where the base case \(i = 0\) is trivially satisfied). It now follows by basic properties of the trace distance that we have \(\varepsilon _{i+1} \le \varepsilon _\mathsf{MAC}+ \sum _{j \le i} \delta _j\). This proves the claim. \(\square \)
4.5 Choosing the Parameters
Let  be the security parameter. Consider a \(\mathsf{MAC}\) with \(\varepsilon _\mathsf{MAC}= 2^{-\lambda }\) and \(|\mathcal{T}| = 2^\lambda \). This can for instance be achieved with the constructions suggested in Sect. 4.2. Also, consider a code \(\mathcal{C}\) with \(|\mathcal{C}| = 2^{3\lambda }\) and \(d = 6\lambda \), so that \(|\mathcal{C}|/2^{d/2} = 1\). The description of the basis key \(\theta \) thus requires \(3\lambda \) bits, and, by Singleton bound, it is necessary that \(n \ge 9\lambda -1\). Then, the bound in Proposition 5 becomes
be the security parameter. Consider a \(\mathsf{MAC}\) with \(\varepsilon _\mathsf{MAC}= 2^{-\lambda }\) and \(|\mathcal{T}| = 2^\lambda \). This can for instance be achieved with the constructions suggested in Sect. 4.2. Also, consider a code \(\mathcal{C}\) with \(|\mathcal{C}| = 2^{3\lambda }\) and \(d = 6\lambda \), so that \(|\mathcal{C}|/2^{d/2} = 1\). The description of the basis key \(\theta \) thus requires \(3\lambda \) bits, and, by Singleton bound, it is necessary that \(n \ge 9\lambda -1\). Then, the bound in Proposition 5 becomes

Hence, the error probability increases at most as \(\big (i \sqrt{i} + 2i + 1\big ) 2^{-\lambda }\) with the number i of executions.
5 Extensions and Variations
We show how to modify our scheme \(\mathsf{QMAC}\) as to offer encryption as well, i.e., to produce an authenticated encryption of \(msg\), and how to deal with noise in the quantum communication; we start with the latter since this is more cumbersome. At the end of the section, we show how to tweak our schemes so as to be able to authenticate and/or encrypt quantum messages as well, and we discuss some variations.
5.1 Dealing with Noise
In order to deal with noise in the quantum communication, we introduce the following primitive. We consider a keyed hash function \(\mathsf{SS}: \mathcal{L} \times \{0,1\}^n \rightarrow \mathcal{S}\) that has the property that given the key \(\ell \), the secure sketch \(s = \mathsf{SS}(\ell ,x)\) of the message x, and a “noisy version” \(x'\) of x, i.e., such that  for some given noise parameter \(\varphi < \frac{1}{2}\), the original message x can be recovered except with probability \(\varepsilon _\mathsf{SS}\). Additionally, we want \(\mathsf{SS}\) to satisfy the message-independence and ideal key-privacy properties from Definitions 2 and 3. Such constructions exist for small enough \(\varphi > 0\), as discussed in Appendix B, based on techniques by Dodis and Smith [8].
for some given noise parameter \(\varphi < \frac{1}{2}\), the original message x can be recovered except with probability \(\varepsilon _\mathsf{SS}\). Additionally, we want \(\mathsf{SS}\) to satisfy the message-independence and ideal key-privacy properties from Definitions 2 and 3. Such constructions exist for small enough \(\varphi > 0\), as discussed in Appendix B, based on techniques by Dodis and Smith [8].
Then, the key for our noise-tolerant quantum message authentication code \(\mathsf{QMAC}^*\) consists of a (initially) uniformly random MAC key \(k \in \mathcal{K}\) for \(\mathsf{MAC}\), an (initially) uniformly random secure-sketch key \(\ell \in \mathcal L\) for \(\mathsf{SS}\), and an (initially) random and independent basis key \(\theta \), chosen from the code \(\mathcal{C}\subset \{0,1\}^n\), and the scheme works as described in Fig. 2.
Theorem 2
If the state before the execution of \(\pi _{\mathsf{QMAC}^*}(msg)\) is of the form \(\rho _{K\varTheta {{{\textsf {\textit{E}}}}}} = \mu _\mathcal{K}\otimes \rho _{\varTheta {{{\textsf {\textit{E}}}}}}\), then for any Eve the state \(\rho _{K \varTheta ' {{{\textsf {\textit{E}}}}}'} = \mathcal{E}{ xe}[\pi _{\mathsf{QMAC}^*}(msg)](\rho _{K\varTheta {{{\textsf {\textit{E}}}}}})\) after the execution satisfies
and

where \(\varepsilon _{\mathsf{MAC}+\mathsf{SS}} = \varepsilon _\mathsf{MAC}+ \varepsilon _\mathsf{SS}\).
Proof
The proof of the first statement, i.e., the bound on \(\mathrm {Guess}(\varTheta '|{{{\textsf {\textit{E}}}}}')\) is exactly like in the proof of Theorem 1, with the only exception that in the one expression where the tag T appears (i.e. in the expression obtained by using Property 1), now S appears as well (along with T); but like T, it disappears again in the next step due to message-independence.
For the bound on \(\delta (KL,U_{\mathcal{K}\times \mathcal{L}} |\varTheta ' {{{\textsf {\textit{E}}}}}')\) we follow closely the proof of Theorem 1 but with the following modifications.
-
1.
The key K is replaced by the key pair (K, L), and the tag T by the tag-secure-sketch pair (T, S), and we observe that we can understand (T, S) to be the hash of the input X under key (K, L) with respect to a hash function that satisfies message-independent and (almost) key-privacy. Indeed, this composed hash function can be understood as being obtained by means of Proposition 4. As such, whenever we argue by means of message-independence (Definition 2) or key-privacy (Definition 3) in the proof of Theorem 1, we can still do so, except that we need to adjust the bound on the uniformity of the key to the new — and now composite — hash function.
-
2.
The auxiliary random variable \(\tilde{D}\), and correspondingly \(\tilde{\varTheta }'\), is defined in a slightly different way: \(\tilde{D}\) is 1 if
 and Eve has not modified the tag T, the secure-sketch S, nor the message \(msg\). The “real” state with D and \(\varTheta '\) is then \((\varepsilon _\mathsf{MAC}+ \varepsilon _\mathsf{SS})\)-close to the modified one with \(\tilde{D}\) and \(\tilde{\varTheta }'\) instead. Correspondingly, the decomposition of the distance to be bounded is then done with respect to the indicated random variable
and Eve has not modified the tag T, the secure-sketch S, nor the message \(msg\). The “real” state with D and \(\varTheta '\) is then \((\varepsilon _\mathsf{MAC}+ \varepsilon _\mathsf{SS})\)-close to the modified one with \(\tilde{D}\) and \(\tilde{\varTheta }'\) instead. Correspondingly, the decomposition of the distance to be bounded is then done with respect to the indicated random variable  instead of \(1_{X = X'}\).
instead of \(1_{X = X'}\). -
3.
When bounding the probability
 , we refer to the game analyzed in Corollary 3 in Appendix A, which applies to the situation here where some slack is given for Bob’s guess.
, we refer to the game analyzed in Corollary 3 in Appendix A, which applies to the situation here where some slack is given for Bob’s guess.
The claimed bound is then obtained by adjusting terms according to the above changes: update the bounds obtained by applying Definition 3 to the updated bound \(\sqrt{\mathrm {Guess}(X|\cdots ) \, |\mathcal{T}| \, |\mathcal{S}|}\), obtained by means of Proposition 4, and inserting the  blow-up when using Corollary 3 instead of Corollary 1, but making use of the observation in Remark 6. \(\square \)
blow-up when using Corollary 3 instead of Corollary 1, but making use of the observation in Remark 6. \(\square \)
In essence, compared to the case with no noise, we have an additional loss due to the \(|\mathcal{S}|\) term, whereas we can neglect the term with  for small enough \(\varphi \). To compensate for this additional loss, we need to have \(\varsigma = \log |\mathcal{S}|\) additional bits of entropy in \(\varTheta \), i.e., we need to choose \(\mathcal{C}\) with \(|\mathcal{C}| = 2^{3\lambda +\varsigma }\) and \(d = 6\lambda +2\varsigma \). By Singleton bound, this requires \(n \ge 9\lambda + 3\varsigma - 1\), and thus puts a bound \(\varsigma < n/3\) on the size of the secure sketch, and thus limits the noise parameter \(\varphi \).Footnote 11
for small enough \(\varphi \). To compensate for this additional loss, we need to have \(\varsigma = \log |\mathcal{S}|\) additional bits of entropy in \(\varTheta \), i.e., we need to choose \(\mathcal{C}\) with \(|\mathcal{C}| = 2^{3\lambda +\varsigma }\) and \(d = 6\lambda +2\varsigma \). By Singleton bound, this requires \(n \ge 9\lambda + 3\varsigma - 1\), and thus puts a bound \(\varsigma < n/3\) on the size of the secure sketch, and thus limits the noise parameter \(\varphi \).Footnote 11
5.2 Adding Encryption
Adding encryption now works pretty straightforwardly. Concretely, our quantum encryption scheme with key recycling \(\mathsf{QENC}^*\) is obtained by means of the following modifications to \(\mathsf{QMAC}^*\). Alice and Bob extract additional randomness from x using an extractor that offers message-independence and key-privacy, and use the extracted randomness as one-time-pad key to en-/decrypt \(msg\). Finally, the resulting ciphertext c is authenticated along with x and s; this is in order to offer authenticity as well and can be omitted if privacy is the only concern.
Security can be proven along the same lines as Theorem 1, respectively Theorem 2 for the noise-tolerant version, and Proposition 5: we simply observe by means of Propositions 3 and 4 that the composition of computing the triple c, s and \(t = \mathsf{MAC}(k,x\Vert c\Vert s)\) from x constitutes a keyed hash function that offers message-independence and key-privacy, and then we can argue exactly as above to show that the (possibly refreshed) key stays secure over many executions. Also, given that the key is secure before an execution, we can control the min-entropy in X as in the proof of Theorem 2 and argue almost-perfect security of the extracted one-time-pad key, implying privacy of the communicated message.
In order to accommodate for the additional entropy that is necessary to extract this one-time-pad key, which is reflected in the adjusted range of the composed keyed hash function, we now have to choose \(\mathcal{C}\) with \(|\mathcal{C}| = 2^{3\lambda +\varsigma +m}\) and \(d = 6\lambda +2\varsigma +2m\), where \(m = \log |\mathcal{MSG}|\); this requires \(n \ge 9\lambda + 3\varsigma + 3m - 1\) by Singleton bound.
5.3 Optimality of the Key Recycling
Our aim was, like in [5, 6], to minimize the number of fresh random bits needed for the key refreshing. In our constructions, where the key is refreshed simply by choosing a new basis key \(\theta \), this number is obviously given by the number of bits needed to represent \(\theta \), i.e., in the above encryption scheme \(\mathsf{QENC}^*\), it is
This is close to optimal for large messages and assuming almost no noise, so that \(m \gg \lambda ,\varsigma \). Indeed, assuming that Eve knows the encrypted message, i.e., we consider a known-plaintext attack, it is not hard to see that for any scheme that offers (almost) perfect privacy of the message, by simply keeping everything that is communicated from Alice to Bob, in particular by keeping all qubits that Alice communicates (which will most likely trigger Bob to reject), Eve can always learn (almost) m bits of Shannon information on the key. As such, it is obviously necessary that the key is updated with (almost) m fresh bits of randomness in case Bob rejects, since otherwise Eve will soon have accumulated too much information on the key.
Note that [5, 6] offers a rigorously proven bound (of roughly m) on the number of fresh bits necessary for key refreshing. However, their notion of key refreshing is stronger than what we require: they require that the refreshed key is close to random and independent of Eve, whereas we merely require that the refreshed key is “secure enough” as to ensure security of the primitive, i.e., authenticity in \(\mathsf{QMAC}\) or \(\mathsf{QMAC}^*\), and privacy (and authenticity) in \(\mathsf{QENC}^*\). Indeed, in our construction we do not require that the basis key is close to random, only that it is hard to guess. However, the above informal argument shows that the bound still applies.
Similarly, one can argue that in any message authentication scheme with error probability \(2^{-\lambda }\), by keeping everything Eve can obtain \(\lambda \) bits of information on the key. Thus, in case of almost no noise, our scheme \(\mathsf{QMAC}^*\) is optimal up to the factor 3.
In our constructions, the number of fresh random bits needed for the key refreshing increases with larger noise. In particular in \(\mathsf{QMAC}^*\), \(\varsigma \) will soon be the dominating term in case we increase the noise level. We point out that it is not clear whether such a dependency is necessary, as we briefly mention in Sect. 6.
5.4 Supporting Quantum Messages
The approach in Sect. 5.2 of extracting a (one-time pad) key also gives us the means to authenticate and/or encrypt quantum messages: we simply use the extracted key as quantum-one-time-pad key [1], or as key for a quantum message authentication code [4]. However, when considering arbitrary quantum messages, honest users anyway need a quantum computer, so one might just as well use the scheme by Damgård et al. to communicate a secret key and use this key for a quantum-one-time-pad or for quantum message authentication, or resort to [10, 16], which additionally offer security against superposition attacks.
5.5 Variations
We briefly mention a few simple variations of our schemes. The first variation is as follows. In \(\mathsf{QMAC}\), instead of choosing x uniformly at random and computing the tag t as \(t = \mathsf{MAC}(k,msg\Vert x)\), we can consider a fixed tag \(t_\circ \in \mathcal{T}\), and choose x uniformly at random subject to \(\mathsf{MAC}(k,msg\Vert x) = t_\circ \). Since \(t_\circ \) is fixed, it does not have to be sent along. In case the classical \(\mathsf{MAC}\), as a keyed hash function, is of the form as in Proposition 2, meaning that the tag is one-time-pad encrypted (which in particular holds for the canonical examples suggested in Sect. 4.2), then Theorem 1 and Proposition 5 still hold. Indeed, if \(\mathsf{MAC}\) is of this form then the concrete choice of \(t_\circ \) is irrelevant for security: if Theorem 1 would fail for one particular choice of \(t_\circ \) then it would fail for any choice, and thus also for a randomly chosen tag, which would then contradict Theorem 1 for the original \(\mathsf{QMAC}\). Similarly, in \(\mathsf{QMAC}^*\) and \(\mathsf{QENC}^*\) we can fix the tag t and the secure sketch s (and ciphertext c), and choose x subject to the corresponding restrictions.
A second variation is to choose the basis key \(\theta \) not as a code word, but uniformly random from \(\{0,1\}^n\). As a consequence, the bounds on the games analyzed in Sect. 3.1 change — indeed, the game analyzed in Proposition 1 then becomes the monogamy-of-entanglement game considered and analyzed in [19] — and therefore we get different bounds in Theorem 1, but conceptually everything should still work out. Our goal was to minimize the number of fresh random bits needed for the key refreshing, which corresponds to the number of bits necessary to describe \(\theta \); this allows us to compare our work with [5, 6] and show that our encryption scheme performs (almost) as good as theirs in this respect. And with this goal in mind, it makes sense to choose \(\theta \) as a codeword: it gives the same guessing probability for x but asks for less entropy in \(\theta \). Choosing \(\theta \) uniformly random from \(\{0,1\}^n\) seems to be the preferred choice for minimizing the quantum communication instead, which would be a very valid objective too.
As an interesting side remark, we observe that with the above variations, our constructions can be understood as following the design principle of the scheme originally proposed by Bennett et al. of encrypting and adding redundancy to the message, and encoding the result into BB84 qubits.
Finally, a last variation we mention is to use the six-state encoding instead of the BB84 encoding. Since the three bases of the six-state encoding have the same so-called maximal overlap, the bounds in Sect. 3.1 carry over unchanged, but we get more freedom in choosing the code \(\mathcal{C}\) in \(\{0,1,2\}^n\) so that fewer qubits need to be communicated for the same amount of entropy in x. Also, when choosing the bases uniformly at random in \(\{0,1,2\}^n\), as in the variation above, we get a slightly larger entropy for x when using the six-state encoding.
6 Conclusion, and Open Problems
We reconsider one of the very first problems that was posed in the context of quantum cryptography, even before QKD, and we give the first solution that offers a rigorous security proof and does not require any sophisticated quantum computing capabilities from the honest users. However, our solution is not the end of the story yet. An intriguing open problem is whether it is possible to do the error correction in a more straightforward way, by just sending the syndrome of x with respect to a fixed suitable code, rather than relying on the techniques from [8]. In return, the scheme would be simpler, it could take care of more noise — Dodis and Smith are not explicit about the amount of noise their codes can correct but it appears to be rather low — and, potentially, the number of fresh random bits needed for key refreshing might not grow with the amount of noise. Annoyingly, it looks like our scheme should still be secure when doing the error correction in the straightforward way, but our proof technique does not work anymore, and there seems to be no direct fix.
From a practical perspective, it would be interesting to see to what extent it is possible to optimize the quantum communication rather than the key refreshing, e.g., by using BB84 qubits with fully random and independent bases, and whether is it possible to beat QKD in terms of quantum communication.
Notes
- 1.
A freshly typeset version of the original manuscript was then published more than 30 years later in [3].
- 2.
In our scheme, \(\theta \) is not uniformly random in \(\{0,1\}^n\) but is chosen to be a code word, as such, its description length is smaller than its physical bit length, and given by the dimension of the code.
- 3.
Their scheme needs \(m+\ell \) fresh random bits for key refreshing, where \(\ell \) is a parameter in their construction, and their scheme fails with probability approximately \(2^{-\ell /2}\).
- 4.
Of course, when Bob sends back the token to confirm, Eve can easily replace it by the reject message and so prevent Alice and Bob from finding agreement, but this is something that Eve can always achieve by “altering the last message”, also in QKD.
- 5.
This means that the system X is actually measured (in the fixed basis \(\{{|x\rangle }\}_{x \in \mathcal X}\)).
- 6.
By our conventions, the probability \(P[\mathcal{M}({{{\textsf {\textit{E}}}}}) \!=\! X]\) is to be understood as \(P[X' \!=\! X]\) for the (purely classical) state \(\rho _{XX'} = \rho _{X\mathcal{M}({{{\textsf {\textit{E}}}}})} = (id_X \otimes \mathcal{M})(\rho _{X{{{\textsf {\textit{E}}}}}}) \in \mathcal{D}(\mathcal{X} \otimes \mathcal{X})\).
- 7.
Here and throughout, for operators K and L, the inequality \(K \le L\) means that \(L-K\) is positive-semidefinite.
- 8.
Here, and similarly in other occasions, \(k\Vert k'\) is simply a synonym for the element \((k,k')\) in the Cartesian product of, here, \(\mathcal{K}\) and \(\mathcal{Y}\), and is mainly used to smoothen notation and avoid expressions like \(\bigl ((k,k'),x\bigr )\).
- 9.
Our definition is tailored to our goal that the key can be re-used unchanged in case the message is accepted by the recipient, Bob, and only needs to be refreshed in case he rejects. In the literature, key-recycling sometimes comes with two refresh procedures, one for the case Bob rejects and one for the case he accepts.
- 10.
Obviously, this requires Alice and Bob to exchange fresh randomness, i.e., the randomness for executing \(\mathsf{Refresh}\), in a reliable and private way; how this is done is not relevant here.
- 11.
We recall that, when using a \(\delta \)-biased family of codes to construct the secure sketch \(\mathsf{SS}\), as discussed in the Appendix B, then \(\varsigma \) does not correspond exactly to the size of the syndrome given by the code, but is determined by the parameter \(\delta \), and is actually somewhat larger than the size of the syndrome.
- 12.
Taking care of such side information, given to Charlie, on Alice’s measurement outcome is not needed for our application, but we get it almost for free.
- 13.
Alternatively, we could simply stick to \(\mathsf{SS}: \mathcal{L} \times \{0,1\}^n \rightarrow \mathcal{SYN}\) but carry along the non-ideal parameter \(\nu \); however, we feel that this additional parameter would make things more cumbersome — but of course would lead to the same end result.
References
Ambainis, A., Mosca, M., Tapp, A., De Wolf, R.: Private quantum channels. In: 41st IEEE FOCS, pp. 547–553 (2000)
Bennett, C.H., Brassard, G.: Quantum cryptography: public key distribution and coin tossing. In: IEEE International Conference on Computers, Systems and Signal Processing, pp. 175–179 (1984)
Bennett, C.H., Brassard, G., Breidbart, S.: Quantum cryptography II: how to re-use a one-time pad safely even if \(P=NP\). Nat. Comput. 13(4), 453–458 (2014)
Barnum, H., Crépeau, C., Gottesman, D., Smith, A., Tapp, A.: Authentication of quantum messages. In: 43rd IEEE FOCS, pp. 449–458 (2002)
Damgård, I., Pedersen, T.B., Salvail, L.: A quantum cipher with near optimal key-recycling. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 494–510. Springer, Heidelberg (2005). doi:10.1007/11535218_30
Damgård, I., Brochmann Pedersen, T., Salvail, L.: How to re-use a one-time pad safely and almost optimally even if \(P =NP\). Nat. Comput. 13(4), 469–486 (2014)
Damgård, I.B., Fehr, S., Salvail, L., Schaffner, C.: Secure identification and QKD in the bounded-quantum-storage model. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 342–359. Springer, Heidelberg (2007). doi:10.1007/978-3-540-74143-5_19
Dodis, Y., Smith, A.: Correcting errors without leaking partial information. In: 37th ACM STOC, pp. 654–663 (2005)
Fehr, S., Schaffner, C.: Randomness extraction via delta-biased masking in the presence of a quantum attacker. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 465–481. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78524-8_26
Garg, S., Yuen, H., Zhandry, M.: New security notions and feasibility results for authentication of quantum data. Manuscript (2016). arXiv:1607.07759v1
Hayden, P., Leung, D., Mayers, D.: Universal composable security of quantum message authentication with key recycling. Talk at QCRYPT 2011, Zürich (2011)
König, R., Renner, R., Schaffner, C.: The operational meaning of min- and max-entropy. IEEE Trans. Inf. Theor. 55(9), 4337–4347 (2009)
Leung, D.: Quantum Vernam cipher. Quantum Inf. Comput. 2(1), 14–34 (2002)
Nisan, N., Zuckerman, D.: Randomness is linear in space. J. Comput. Syst. Sci. 52(1), 43–52 (1996)
Oppenheim, J., Horodecki, M.: How to reuse a one-time pad and other notes on authentication, encryption and protection of quantum information. Phys. Rev. A 72, 042309 (2005)
Portmann, C.: Quantum authentication with key recycling. Manuscript. arXiv.org/abs/1610.03422v1 (2016). Also to appear in these proceedings
Renner, R.: Security of quantum key distribution. Ph.D. thesis, ETH Zürich, No. 16242 (2005)
Radhakrishnan, J., Ta-Shma, A.: Bounds for dispersers, extractors, and depth-two superconcentrators. SIAM J. Comput. 13(1), 2–24 (2000)
Tomamichel, M., Fehr, S., Kaniewski, J., Wehner, S.: One-sided device-independent QKD and position-based cryptography from monogamy games. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 609–625. Springer, Heidelberg (2013). doi:10.1007/978-3-642-38348-9_36
Acknowledgments
The authors would like to thank Ivan Damgård and Christian Schaffner for interesting discussions related to this work, and Christopher Portmann for comments on an earlier version of the paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix
A Yet Another (Version of the) Guessing Game
We consider a variant of the guessing game from Sect. 3.1 where Bob and Charlie need to guess Alice’s measurement outcome. In the variation considered here, we give some slack to Bob in that it is good enough if his guess is close enough (in Hamming distance) to Alice’s measurement outcome, and Charlie is given some (deterministic) classical side information on Alice’s measurement outcome before he has to announce his guess.Footnote 12 We show that, if the minimal distance d of the code \(\mathcal{C}\) is large enough, this does not help Bob and Charlie significantly. This is in line with the intuition that, for large enough d, the optimal strategy for Bob and Charlie is to pre-guess Alice’s choice of bases.
Proposition 6
Let \(\mathcal {H}_{{{\textsf {\textit{A}}}}}\) be a n-qubit system, and let \(\mathcal {H}_{{{\textsf {\textit{B}}}}}\) and \(\mathcal {H}_{{{\textsf {\textit{C}}}}}\) be arbitrary quantum systems. Also, let  be a parameter and \(f:\{0,1\}^n \rightarrow \mathcal{Y}\) a function. Consider a state \(\rho _{\varTheta {{{\textsf {\textit{A}}}}}{{{\textsf {\textit{B}}}}}{{{\textsf {\textit{C}}}}}} = \mu _{\mathcal{C}} \otimes \rho _{{{{\textsf {\textit{A}}}}}{{{\textsf {\textit{B}}}}}{{{\textsf {\textit{C}}}}}} \in \mathcal{D}(\mathcal{C}\otimes \mathcal {H}_{{{\textsf {\textit{A}}}}}\otimes \mathcal {H}_{{{\textsf {\textit{B}}}}}\otimes \mathcal {H}_{{{\textsf {\textit{C}}}}})\), and let
be a parameter and \(f:\{0,1\}^n \rightarrow \mathcal{Y}\) a function. Consider a state \(\rho _{\varTheta {{{\textsf {\textit{A}}}}}{{{\textsf {\textit{B}}}}}{{{\textsf {\textit{C}}}}}} = \mu _{\mathcal{C}} \otimes \rho _{{{{\textsf {\textit{A}}}}}{{{\textsf {\textit{B}}}}}{{{\textsf {\textit{C}}}}}} \in \mathcal{D}(\mathcal{C}\otimes \mathcal {H}_{{{\textsf {\textit{A}}}}}\otimes \mathcal {H}_{{{\textsf {\textit{B}}}}}\otimes \mathcal {H}_{{{\textsf {\textit{C}}}}})\), and let

where \(\mathcal{N}_{\varTheta {{{\textsf {\textit{B}}}}}\rightarrow X'}\) is an arbitrary measurement of system \({{{\textsf {\textit{B}}}}}\) controlled by \(\varTheta \), and \(\mathcal{N}_{\varTheta f(X) {{{\textsf {\textit{C}}}}}\rightarrow X''}\) is an arbitrary measurement of system \({{{\textsf {\textit{C}}}}}\) controlled by \(\varTheta \) and f(X).
Then, it holds that

where h is the binary entropy function.
Proof
Here, we can write
for projectors

where  denotes the set of stings with Hamming weight at most
denotes the set of stings with Hamming weight at most  . For any \(\theta \ne \theta ' \in \mathcal{C}\), we can upper bound \(\tilde{\varPi }^\theta \) and \(\tilde{\varPi }^{\theta '}\) by
. For any \(\theta \ne \theta ' \in \mathcal{C}\), we can upper bound \(\tilde{\varPi }^\theta \) and \(\tilde{\varPi }^{\theta '}\) by

and

respectively, where \(\varGamma _e^\theta \) and \(\varDelta _y^{\theta '}\) are like \(\varGamma ^\theta \) and \(\varDelta ^{\theta '}\), as defined in the proof of Proposition 1, for certain concrete choices of the POVM’s \(\{P^\theta _x\}_x\) and \(\{Q^{\theta '}_x\}_x\) that depend on e and y, respectively. As such, we get that

Since we still have that \(\bigl \Vert \tilde{\varPi }^\theta \tilde{\varPi }^\theta \bigr \Vert = \bigl \Vert \tilde{\varPi }^\theta \bigr \Vert = 1\), the claim follows. \(\square \)
By means of the techniques from Sect. 3.1, we can extend the result to the case where Bob and Charlie have a-priori quantum side information on Alice’s choice of bases.
Corollary 3
Let \(\mathcal {H}_{{{\textsf {\textit{A}}}}}\) be a n-qubit system, and let \(\mathcal {H}_{{{\textsf {\textit{B}}}}}, \mathcal {H}_{{{\textsf {\textit{C}}}}}\) and \(\mathcal {H}_{{{\textsf {\textit{E}}}}}\) be arbitrary quantum systems. Also, let  be a parameter and \(f:\{0,1\}^n \rightarrow \mathcal{Y}\) a function. Consider a state \(\rho _{\varTheta {{{\textsf {\textit{E}}}}}} \in \mathcal{D}(\mathcal{C}\otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\), and let
be a parameter and \(f:\{0,1\}^n \rightarrow \mathcal{Y}\) a function. Consider a state \(\rho _{\varTheta {{{\textsf {\textit{E}}}}}} \in \mathcal{D}(\mathcal{C}\otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\), and let
where \(\mathcal{Q}_{{{{\textsf {\textit{E}}}}}\rightarrow {{{\textsf {\textit{A}}}}}{{{\textsf {\textit{B}}}}}{{{\textsf {\textit{C}}}}}}\) is a CPTP map acting on \({{{\textsf {\textit{E}}}}}\), and let

as in Proposition 6 above. Then, it holds that

Remark 6
In line with the remarks in Sect. 3.1, if Bob “measures correctly” but is still given some slack, and, say, Charlie is given no side information on Alice’s outcome, the bound relaxes to

B On the Existence of Suitable Secure Sketches
In [8, Lemma 5], Dodis and Smith show that for any constant \(0< \lambda < 1\), there exists an explicitly constructible family of binary linear codes \(\{\mathcal{C}_i\}_{i \in \mathcal I}\) in \(\{0,1\}^n\) with dimension k that efficiently correct a constant fraction of errors and have square bias \(\delta ^2 \le 2^{-\lambda n}\). Their Lemma 4 then shows that the keyed hash function \(\mathsf{Ext}: \mathcal{I} \times \{0,1\}^n \rightarrow \mathcal{SYN} = \{0,1\}^{n-k}\),  is a strong extractor, where \(syn_i(x)\) is the syndrome with respect to the code \(\mathcal{C}_i\). More precisely, the generalization of their result to quantum side information by Fehr and Schaffner [9] shows that if \(\rho _{IX{{{\textsf {\textit{E}}}}}} = \mu _\mathcal{I} \otimes \rho _{X {{{\textsf {\textit{E}}}}}} \in \mathcal{D}(\mathcal{I} \otimes \mathcal{X} \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\) then
is a strong extractor, where \(syn_i(x)\) is the syndrome with respect to the code \(\mathcal{C}_i\). More precisely, the generalization of their result to quantum side information by Fehr and Schaffner [9] shows that if \(\rho _{IX{{{\textsf {\textit{E}}}}}} = \mu _\mathcal{I} \otimes \rho _{X {{{\textsf {\textit{E}}}}}} \in \mathcal{D}(\mathcal{I} \otimes \mathcal{X} \otimes \mathcal {H}_{{{\textsf {\textit{E}}}}})\) then
It follows from Proposition 2 that the secure sketch

where \(\mathcal{L} := \mathcal{I} \times \mathcal{SYN}\), offers uniformity and \(\nu \)-key-privacy with parameter \(\nu = \delta 2^{n/2}/\sqrt{|\mathcal{SYN}|} = \delta 2^k\).
Dodis and Smith are not explicit about the size \(n-k\) of the syndrome in their construction, but looking at the details, we see that \(n-k\le \log (\delta ^2 \, 2^n)\). As such, by artificially extending the range \(\mathcal{SYN} = \{0,1\}^{n-k}\) of \(\mathsf{SS}\) to a set \(\mathcal{S} = \{0,1\}^{\varsigma }\) of bit strings of size \(\varsigma := \log (\delta ^2 \, 2^n)\), and re-defining \(\mathsf{SS}\) to map \((i\Vert b,x)\) to \(syn_i(x)+b\) padded with sufficiently many 0’s, we get that the secure sketch \(\mathsf{SS}: \mathcal{L} \times \{0,1\}^n \rightarrow \mathcal{S}\) is message-independent and offers ideal key-privacy.Footnote 13
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Fehr, S., Salvail, L. (2017). Quantum Authentication and Encryption with Key Recycling. In: Coron, JS., Nielsen, J. (eds) Advances in Cryptology – EUROCRYPT 2017. EUROCRYPT 2017. Lecture Notes in Computer Science(), vol 10212. Springer, Cham. https://doi.org/10.1007/978-3-319-56617-7_11
Download citation
DOI: https://doi.org/10.1007/978-3-319-56617-7_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-56616-0
Online ISBN: 978-3-319-56617-7
eBook Packages: Computer ScienceComputer Science (R0)


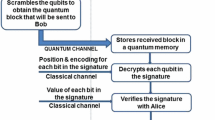




 and Eve has not modified the tag T, the secure-sketch S, nor the message
and Eve has not modified the tag T, the secure-sketch S, nor the message  instead of
instead of  , we refer to the game analyzed in Corollary
, we refer to the game analyzed in Corollary 