Abstract
As suggested by the title, it has recently become clear that theorems of Nonstandard Analysis (NSA) give rise to theorems in computability theory (no longer involving NSA). Now, the aforementioned discipline divides into classical and higher-order computability theory, where the former (resp. the latter) sub-discipline deals with objects of type zero and one (resp. of all types). The aforementioned results regarding NSA deal exclusively with the higher-order case; we show in this paper that theorems of NSA also give rise to theorems in classical computability theory by considering so-called textbook proofs.
This research was supported by FWO Flanders, the John Templeton Foundation, the Alexander von Humboldt Foundation, LMU Munich (via the Excellence Initiative), and the Japan Society for the Promotion of Science. The work was done partially while the author was visiting the Institute for Mathematical Sciences, National University of Singapore in 2016. The visit was supported by the Institute.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The distinction ‘classical versus higher-order’ is not binary as e.g. continuous functions on the reals may be represented by type one objects (See e.g. [23, II.6.1]).
- 2.
The superscript ‘fin’ in (I) means that x is finite, i.e. its number of elements are bounded by a natural number.
- 3.
The language of E-PA \(_{\text {st}}^{\omega *}\) contains a symbol \(\text {st}_{\sigma }\) for each finite type \(\sigma \), but the subscript is essentially always omitted. Hence \({\mathcal {T}}^{*}_{\text {st}}\) is an axiom schema and not an axiom.
- 4.
A term is called closed in [1] (and in this paper) if all variables are bound via lambda abstraction. Thus, if \({\underline{x}}, {\underline{y}}\) are the only variables occurring in the term t, the term \((\lambda {\underline{x}})(\lambda {\underline{y}})t({\underline{x}}, {\underline{y}})\) is closed while \((\lambda {\underline{x}})t({\underline{x}}, {\underline{y}})\) is not. The second axiom in Definition 2.3 thus expresses that \(\text {st}_{\tau }\big ((\lambda {\underline{x}})(\lambda {\underline{y}})t({\underline{x}}, {\underline{y}})\big )\) if \((\lambda {\underline{x}})(\lambda {\underline{y}})t({\underline{x}}, {\underline{y}})\) is of type \(\tau \).
- 5.
Recall the definition of closed terms from [1] as sketched in Footnote 4.
- 6.
To ‘apply this formula \(k_{0}+1\) times’, apply \(\textsf {HAC} _{\textsf {int} }\) to \((\forall ^{\text {st}}n)(\exists ^{\text {st}} N, M\ge n)(|c_{N}- c_{M}|\ge \frac{1}{k_{0}})\) to obtain standard \(F^{0\rightarrow 0^{*}}\) and define G(n) as the maximum of F(n)(i) for \(i<|F(n)|\). Then \((\forall ^{\text {st}}n)(\exists N, M\ge n)(N, M\le G(n)\wedge |c_{N}- c_{M}|\ge \frac{1}{k_{0}})\) and iterate the functional G at least \(k_{0}+1\) times to obtain the desired contradiction.
- 7.
For instance, written out in full ‘\(0\le \varphi _{e}^{A}(n)\le \varphi _{e}^{A}(n+1)\le 1\)’ from \(\textsf {MCT} _{\textsf {ef} }^{A}(t)\) is:
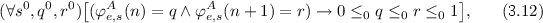
where we also omitted the coding of rationals.
- 8.
Bishop (See [4, p. 513], [2, p. 1], and [3], which is the review of [11]) and Connes (See [6, p. 6207] and [5, p. 26]) have made rather strong claims regarding the non-constructive nature of Nonstandard Analysis. Their arguments have been investigated in remarkable detail and were mostly refuted (See e.g. [8,9,10]).
- 9.
Suppose \(f_{1}=11\dots \) and \(\mu ^{2}\) from \((\mu ^{2})\) is continuous; then there is \(N_{0}^{0}\) such that \((\forall g^{1})(\overline{f_{1}}N_{0}={\overline{g}}N_{0}\rightarrow \mu (f_{1})=_{0}\mu (g))\). Let \(N_{1}\) be the maximum of \(N_{0}\) and \(\mu (f_{1})\). Then \(g_{0}:=\overline{f_{1}}N_{1}*00\dots \) satisfies \(\overline{f_{1}}N_{1}=\overline{g_{0}}N_{1}\), and hence \(\mu (f_{1})=\mu (g_{0})\) and \(f_{1}(\mu (f_{1}))=g_{0}(\mu (g_{0}))\), but the latter is 0 by the definition of \(g_{0}\) and \(\mu \), a contradiction..
- 10.
If a functional has an associate, it must be continuous on Baire space. We established in Footnote 9 that \((\mu ^{2})\) cannot be continuous, and thus cannot have an associate.
References
van den Berg, B., Briseid, E., Safarik, P.: A functional interpretation for nonstandard arithmetic. Ann. Pure Appl. Logic 163(12), 1962–1994 (2012)
Bishop, E.: Aspects of constructivism. Notes on the Lectures Delivered at the Tenth Holiday Mathematics Symposium, New Mexico State University, Las Cruces, 27–31 December 1972
Bishop, E.: Review of [11]. Bull. Amer. Math. Soc 81(2), 205–208 (1977)
Bishop, E.: The crisis in contemporary mathematics. In: Proceedings of the American Academy Workshop on the Evolution of Modern Mathematics, pp. 507–517 (1975)
Connes, A.: An interview with Alain Connes. EMS Newslett. 63, 25–30 (2007). http://www.mathematics-in-europe.eu/maths-as-a-profession/interviews
Connes, A.: Noncommutative geometry and reality. J. Math. Phys. 36(11), 6194–6231 (1995)
Dzhafarov, D.D.: Reverse Mathematics Zoo. http://rmzoo.uconn.edu/
Kanovei, V., Katz, M.G., Mormann, T.: Tools, objects, and chimeras: Connes on the role of hyperreals in mathematics. Found. Sci. 18(2), 259–296 (2013)
Katz, M.G., Leichtnam, E.: Commuting and noncommuting infinitesimals. Am. Math. Mon. 120(7), 631–641 (2013)
Keisler, H.J.: Letter to the editor. Not. Am. Math. Soc. 24, 269 (1977)
Keisler, H.J.: Elementary Calculus. Prindle, Weber and Schmidt, Boston (1976)
Kohlenbach, U.: Applied Proof Theory: Proof Interpretations and Their Use in Mathematics. Springer Monographs in Mathematics. Springer, Berlin (2008)
Kohlenbach, U.: Higher order reverse Mathematics. In: Reverse Mathematics 2001. Lecture Notes in Logic, vol. 21, pp. 281–295. ASL (2005)
Kohlenbach, U.: Foundational and mathematical uses of higher types. In: Reflections on the Foundations of Mathematics (Stanford, CA, 1998). Lecture Notes in Logic, vol. 15, pp. 92–116. ASL (2002)
Nelson, E.: Internal set theory: a new approach to Nonstandard Analysis. Bull. Am. Math. Soc. 83(6), 1165–1198 (1977)
Robinson, A.: Non-standard Analysis. North-Holland, Amsterdam (1966)
Sanders, S.: The Gandy-Hyland functional and a hitherto unknown computational aspect of Nonstandard Analysis (2015). Submitted. http://arxiv.org/abs/1502.03622
Sanders, S.: The unreasonable effectiveness of Nonstandard Analysis (2015). Submitted. arXiv: http://arxiv.org/abs/1508.07434
Sanders, S.: On the connection between Nonstandard Analysis and classical computability theory. In: Preparation (2016)
Sanders, S.: The taming of the reverse mathematics zoo. (2015). Submitted. http://arxiv.org/abs/1412.2022
Sanders, S.: The refining of the taming of the reverse mathematics zoo. Notre Dame J. Formal Logic (2016, to appear). http://arxiv.org/abs/1602.02270
Simpson, S.G. (ed.): Reverse Mathematics 2001. Lecture Notes in Logic, vol. 21. ASL, La Jolla (2005)
Simpson, S.G. (ed.): Subsystems of Second Order Arithmetic. Perspectives in Logic, 2nd edn. CUP, Cambridge (2009)
Troelstra, A.S.: Metamathematical Investigation of Intuitionistic Arithmetic and Analysis. Lecture Notes in Mathematics, vol. 344. Springer, Berlin (1973)
Acknowledgement
The author would like to thank Richard Shore, Anil Nerode, and Vasco Brattka for their valuable advice and encouragement.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Sanders, S. (2017). From Nonstandard Analysis to Various Flavours of Computability Theory. In: Gopal, T., Jäger , G., Steila, S. (eds) Theory and Applications of Models of Computation. TAMC 2017. Lecture Notes in Computer Science(), vol 10185. Springer, Cham. https://doi.org/10.1007/978-3-319-55911-7_40
Download citation
DOI: https://doi.org/10.1007/978-3-319-55911-7_40
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-55910-0
Online ISBN: 978-3-319-55911-7
eBook Packages: Computer ScienceComputer Science (R0)