Strong Optimal Controls in a Steady-State Problem of Complex Heat Transfer

Abstract

An optimal control problem of steady-state complex heat transfer with monotone objective functionals is under consideration. A coefficient function appearing in boundary conditions and reciprocally corresponding to the reflection index of the domain surface is considered as control. The concept of strong maximizing (resp. strong minimizing) optimal controls, i.e. controls that are optimal for all monotone objective functionals, is introduced. The existence of strong optimal controls is proven, and optimality conditions for such controls are derived. An iterative algorithm for computing strong optimal controls is proposed.

1 Introduction

The interest in studying problems of complex heat transfer (where the radiative, convective, and conductive contributions are simultaneously taken into account) is motivated by their importance for many engineering applications. The common feature of such processes is the radiative heat transfer dominating at high temperatures. The radiative heat transfer equation (RTE) is a first order integro-differential equation governing the radiation intensity. The radiation traveling along a path is attenuated as a result of absorption and scattering. The precise derivation and analysis of such models can be found in the monograph [1].

Solutions to the RTE can be represented in the form of the Neumann series whose terms are powers of an integral operator applied to a certain start function. The terms can be calculated using a Monte Carlo method, which may be interpreted as tracking the history of energy bundles from emission to adsorption on the boundary or within the participating medium. The method assumes that the bundles start from random points, propagate in random directions, and show the energy exchange due to random scattering (see e.g. [2]).

A way to avoid solving the integro-differential RTE is the use of expansions of the local intensity in terms of spherical harmonics, with truncation to N terms in the series, and substitution into the moments of the differential form of the RTE (see e.g. [1]). This approach leads to the $P_N$ approximations, where N is the approximation order. Especially interesting is the $P_1$ (diffusion) approximation because it does not require high computational efforts. Using the diffusion model instead of the integro-differential RTE becomes popular, and this is substantiated in various applications (e.g., image reconstruction [3] and modeling the radiative transfer in biological tissues [4]). In this connection, the work [5] can also be mentioned: It is shown there that the diffusion approximation yields a good accuracy for temperatures up to $1200^{\circ }$C. Thus, the diffuse approximation can successfully be applied to various heat transfer problems where very high accuracy is not required.

Optimal control problems of complex heat transfer draw the interest of researchers working in applied fields, e.g. glass manufacturing [6,7,8], laser thermotherapy [9], the design of cooling systems [10, 11], etc. A considerable number of works is devoted to control problems related to evolutionary systems describing radiative heat transfer (see e.g. [6,7,8,9,10, 12,13,14]). In the above-mentioned works, the transfer of radiation is described by an integral-differential equation or by its approximations. The temperature field is simulated by the conventional evolutionary heat transfer equation with additional source terms accounting for the contribution of radiation.

As for steady-state problems of complex heat transfer, there are few results in this direction. It is worth to mention the work [11], where an optimal boundary multiplicative control problem for a steady-state complex heat transfer model is considered. The problem is formulated as the maximization of the energy outflow from the model domain by controlling reflection properties of the boundary. The solvability of this problem is proven based on new a priori estimates for solutions of the model equations. Moreover, an analogue of the bang-bang principle arising in control theory for ordinary differential equations is proven. Notice that the optimization of energy in/out flow, which improves heating/cooling systems, is a quite popular problem in many engineering applications. In [15,16,17,18], similar problems are considered in the context of shape optimization.

In the current work, a conductive-convective-radiative heat transfer control problem with monotone objective functionals is under consideration. The definition of monotone functionals looks as follows. Let $\theta$ and $\varphi$ be the state variables of the model, and $J(\theta ,\varphi )$ the objective functional. This functional is called monotone increasing (resp. decreasing) if the relations $\theta _1\le \theta _2$ and $\varphi _1\le \varphi _2$, a. e., imply the relation $J(\theta _1,\varphi _1)\le J(\theta _2,\varphi _2)$ (resp. $J(\theta _1,\varphi _1)\ge J(\theta _2,\varphi _2)$). It should be noticed that such functionals appear very often in applications. For example, the objective functional in the problem of maximum energy outflow is a monotone one.

Moreover, the concept of strong minimizing (resp. maximizing) optimal controls, i.e. controls that yield minimal (resp. maximal) state functions is introduced. Sufficient optimality conditions that do not involve solutions of adjoint equations are derived.

An iterative algorithm for finding strong optimal controls is proposed, and its convergence is proven. This, in particular, proves the existence of strong optimal controls.

2 Problem Setting

The normalized diffusion model, $P_1$ approximation, of radiative, conductive, and convective heat transfer in a bounded domain $\varOmega \subset \mathbb {R}^3$ looks as follow (see [1, 19,20,21]):

$$\begin{aligned} - a\varDelta \theta + \mathbf v \cdot \nabla \theta + b\kappa _a(|\theta |\theta ^3- \varphi )=0, \end{aligned}$$

(1)

$$\begin{aligned} -\alpha \varDelta \varphi + \kappa _a(\varphi -|\theta |\theta ^3)=0. \end{aligned}$$

(2)

Here, $\theta$ is the normalized temperature, $\varphi$ the normalized intensity of radiation averaged over all direction, $\kappa _a$ the absorbtion coefficient, and $\mathbf v$ a prescribed velocity field. The constants a, b, and $\alpha$ are defined by the formulas

$$a=\frac{k}{\rho c_p},\quad b = \frac{4\sigma n^2 T_{max}^3}{\rho c_p}, \quad \alpha =\frac{1}{3\kappa - A \kappa _s},$$

where k is the thermal conductivity, $c_p$ the specific heat capacity, $\rho$ the density, $\sigma$ the Stefan-Boltzmann constant, n the refractive index, $T_{max}$ the maximum temperature in unnormalized model, $\kappa := \kappa _s + \kappa _a$ the extinction coefficient, $\kappa _s$ the scattering coefficient. The coefficient $A \in [-1,1]$ describes the anisotropy of scattering. The case $A=0$ corresponds to isotropic scattering.

The following boundary conditions on $\varGamma :=\partial \varOmega$ are imposed:

$$\begin{aligned} a\partial _n \theta + \beta (\theta - \theta _b) = 0,\qquad \alpha \partial _n \varphi + u(\varphi - \theta _b^4) = 0. \end{aligned}$$

(3)

Here, $\partial _n$ denotes the derivative in the direction of the outward normal $\mathbf n$; $\theta _b= \theta _b(x)$, $x \in \varGamma$, and $\beta =\beta (x)$, $x\in \varGamma$, are given non-negative functions describing the normalized external temperature and the normalized overall heat transfer coefficient, respectively. The function $u = u(x)$, $x \in \varGamma$, describing the reflection properties of the boundary is considered as control input.

The minimum (resp. maximum) control problem is formulated as finding a control $\widehat{u} \in L^\infty (\varGamma )$, $\widehat{u}(x) \in [u_1(x), u_2(x)], \text { a.e. on } \varGamma$, such that for any admissible control u the following relation holds: $y(\widehat{u}) \le y(u)$ (resp. $y(\widehat{u}) \ge y(u)$, a.e. in $\varOmega$, where $y(\widehat{u})$ and y(u) are solution pairs satisfying relations (1)–(3) with $\widehat{u}$ and u, respectively. Here, $u_1, u_2$ are given non-negative functions defining inequality constraints imposed on the control.

It is clear that the control $\widehat{u}$ is optimal in the sense of minimization (resp. maximization) of monotone functionals outlined in Sect. 1.

3 Problem Formalization

Assume that $\varOmega$ be a bounded Lipschitz domain. Let $L^p$, $p \in [1,\infty ]$, denotes the Lebesgue space, and $H^s(\varOmega )$ the Sobolev space $W^s_2(\varOmega )$. Moreover, let the following conditions be fulfilled:

• (i) $\mathbf v \in H^1(\varOmega )$, $\text {div}\,\mathbf v = 0;$

• (ii) $\beta ,u_1, u_2, \theta _b \in L^{\infty }(\varGamma ),\; 0< \beta _0 \le \beta ,\; 0 < u_0 \le u_1 \le u_2,\;\theta _b \ge 0,\; \beta _0,u_0 \text { are const;}$

• (iii) $\beta + \mathbf v \cdot \mathbf n \ge 0$, if $\mathbf v \cdot \mathbf n < 0.$

Denote $H = L^2(\varOmega )$, $V = H^1(\varOmega )$, and define the norms, $\Vert \cdot \Vert$ and $\Vert \cdot \Vert _V$, in H and V, respectively, as follows:

$$ \Vert f\Vert ^2 = (f, f), \quad \Vert f\Vert _V^2 = \Vert f\Vert ^2 + \Vert \nabla f\Vert ^2,\quad (f, g) = \int \limits _\varOmega f(x)g(x)dx. $$

Definition 1

A pair $\{\theta ,\varphi \} \in V\times V$ is called a (weak) solution of the problem (1)–(3) if

$$\begin{aligned} a(\nabla \theta , \nabla \eta ) + (\mathbf {v}\cdot \nabla \theta + b\kappa _a(|\theta |\theta ^3-\varphi ), \eta )+\int \limits _{\varGamma }\beta (\theta - \theta _b)\eta d\varGamma = 0 \quad \forall \eta \in V, \end{aligned}$$

(4)

$$\begin{aligned} \alpha (\nabla \varphi , \nabla \psi ) + \kappa _a(\varphi - |\theta |\theta ^3, \psi )+ \int \limits _{\varGamma } u (\varphi -\theta _b^4)\psi d\varGamma = 0 \quad \forall \psi \in V. \end{aligned}$$

(5)

Theorem 1

(see [21]). Let the conditions (i)–(iii) be true. Then the problem (1)–(3) is uniquely solvable, a weak solution $\{\theta ,\varphi \}$ belongs to $\big (L^{\infty }(\varOmega )\big )^2$ and satisfies the inequalities $0 \le \theta \le M$ and $0 \le \varphi \le M^4$, where $M = \Vert \theta _b\Vert _{L^{\infty }(\varGamma )}$, and the following estimate is true:

$$\begin{aligned} \Vert \theta \Vert _{V}+\Vert \varphi \Vert _{V} \le C, \end{aligned}$$

(6)

where C depends only on $\varOmega$, M, $\Vert \beta \Vert _{L^\infty (\varGamma )}$, $\Vert u\Vert _{L^\infty (\varGamma )}$, $\Vert \mathbf v\Vert _{V}$, a, $\alpha$, b, and $\kappa _a$.

Now, the conception of strong optimal controls will be introduced. Denote by $U_{ad} = \{u \in L^\infty (\varGamma ) :u_1 \le u \le u_2\}$ the set of admissible controls.

Definition 2

A function $\widehat{u} \in U_{ad}$ is called strong minimizing (resp. maximizing) optimal control if $\widehat{\theta }\le \theta$ and $\widehat{\varphi }\le \varphi$ (resp. $\widehat{\theta }\ge \theta$ and $\widehat{\varphi }\ge \varphi$), a.e. in $\varOmega$, for all $u \in U_{ad}$, where $\{\widehat{\theta },\widehat{\varphi }\}$ and $\{\theta ,\varphi \}$ are solution pairs corresponding to $\widehat{u}$ and u, respectively.

Definition 3

A functional $J :[V \cap L^\infty (\varOmega )]^2 \rightarrow \mathbb R$ is called monotone if the relations $0 \le \theta _1 \le \theta _2$ and $0 \le \varphi _1 \le \varphi _2$, a.e. in $\varOmega$, imply the inequality $J(\theta _1,\varphi _1) \le J(\theta _2,\varphi _2)$, where $\theta _1,\theta _2,\varphi _1$, and $\varphi _2$ are arbitrary functions from $V \cap L^\infty (\varOmega )$.

Consider examples of monotone functionals.

1. The sum of weighted norms of $\theta$ and $\varphi$:

$$\begin{aligned} J(\theta ,\varphi ) = \int _\varOmega \left( r_1\theta ^2 + r_2\varphi ^2 \right) dx, \end{aligned}$$

(7)

where $r_1$ and $r_2 \in L^\infty (\varOmega )$ are non-negative given functions.

2. Energy flow through a part of the boundary. Let $\varGamma _1 \subset \varGamma$ be an outflow boundary part, i.e. $\mathbf v \cdot \mathbf n \ge 0$ on $\varGamma _1$. The density of the energy flow is defined by the formula

$$ \mathbf q = -a\nabla \theta + \theta \mathbf v - \alpha b\nabla \varphi , $$

and therefore, the energy outflow through $\varGamma _1$ is given by the functional

$$\begin{aligned} J(\theta ,\varphi ) = \int _{\varGamma _1}\mathbf q \cdot \mathbf n \, d\varGamma = \int _{\varGamma _1}(\beta (\theta - \theta _b) + \theta \mathbf v \cdot \mathbf n + b\gamma (\varphi - \theta _b^4))d\varGamma . \end{aligned}$$

(8)

Here, $\gamma$ is a constant that replaces the function u in the boundary condition for $\varphi$ on the opening $\varGamma _1$. If the Marshak boundary condition [22] is used, then $\gamma =0.5$.

Say that a triple $\{\theta ,\varphi ,u\}$ is admissible if $u \in U_{ad}$ and $\{\theta ,\varphi \} \in V\times V$ is a solution of the problem (1)–(3) corresponding to the control u. Denote the set of all admissible triples by $\mathcal U$.

Let J be a monotone functional (see Definition 3). Consider the following optimization problems:

Problem 1:

$$ J(\theta ,\varphi ) \rightarrow \min ,\qquad \{\theta ,\varphi ,u\} \in \mathcal U. $$

Problem 2:

$$ J(\theta ,\varphi ) \rightarrow \max ,\qquad \{\theta ,\varphi ,u\} \in \mathcal U. $$

A solution $\{\theta ,\varphi ,u\}$ of Problem 1 or 2 will be called optimal triple, and its components $\{\theta ,\varphi \}$ and u will be referred as optimal state and optimal control, respectively.

The following proposition is an obvious corollary of Definitions 2 and 3, accounting for that the objective functionals of Problems 1 and 2 are monotone.

Proposition 1

A strong minimizing (resp. maximizing) optimal control solves Problem 1 (resp. Problem 2).

The next section describes the derivation of sufficient optimality conditions characterizing strong optimal controls and discusses the question of uniqueness. These considerations give rise to an iterative numerical method that always converges to a strong optimal control, which, in particular, proves the existence of such controls.

4 Conditions of Optimality

Similar to [21], introduce nonlinear operators $F_1: L^{\infty }(\varOmega )\times U_{ad}\rightarrow L^{\infty }(\varOmega )\cap H^1(\varOmega )$ and $F_2: L^{\infty }(\varOmega )\rightarrow L^{\infty }(\varOmega )\cap H^1(\varOmega )$ as follows: $\varphi =F_1(\theta , u)$ if

$$\begin{aligned} \alpha (\nabla \varphi ,\nabla v) + \int _\varGamma u\,(\varphi -\theta _b^4)vd\varGamma +\kappa _a(\varphi , v)= \kappa _a(|\theta |\theta ^3,v) \quad \forall v\in V, \end{aligned}$$

(9)

and $\theta =F_2(\varphi )$ if

$$\begin{aligned} a(\nabla \theta ,\nabla v) + \int _\varGamma \beta (\theta -\theta _b)vd\varGamma + (\mathbf v\nabla \theta ,v) + b\kappa _a(|\theta |\theta ^3,v)= b\kappa _a(\varphi , v) \quad \forall v\in V. \end{aligned}$$

(10)

Notice that $\{\widehat{\theta },\widehat{\varphi }\}$ is a weak solution of the problem (1)–(3) with a control $\widehat{u}$ if and only if $\widehat{\theta }=F_2(F_1(\widehat{\theta },\widehat{u}))$, $\widehat{\varphi }=F_1(F_2(\widehat{\varphi }), \widehat{u}).$ The operators $F_1$ and $F_2$ have the following properties (see [21]):

• 1. If $u\in U_{ad}$, $M = \Vert \theta _b\Vert _{L^{\infty }(\varGamma )}$, $0\le \theta \le M$, and $0\le \varphi \le M^4$, a.e. in $\varOmega$, then $0\le F_1(\theta ,u)\le M^4$ and $0\le F_2(\varphi )\le M$, a.e. in $\varOmega$.

• 2. If $u\in U_{ad}$, $\theta _1\le \theta _2$, and $\varphi _1\le \varphi _2$, a.e. in $\varOmega$, then $F_1(\theta _1,u)\le F_1(\theta _2,u)$ and $F_2(\varphi _1)\le F_2(\varphi _2)$, a.e. in $\varOmega$.

Define an operator $U :L^\infty (\varGamma ) \rightarrow L^\infty (\varGamma )$ as follows:

$$ U(\eta )(s) = {\left\{ \begin{array}{ll} u_1(s), &{} \eta (s) - \theta _b^4(s) < 0,\\ u_2(s), &{} \eta (s) - \theta _b^4(s) > 0. \end{array}\right. } $$

Lemma 1

If $\widetilde{u}\in U_{ad}$, $\theta \le \widetilde{\theta }$ a.e. in $\varOmega$, $\varphi = F_1(\theta , u)$, $\widetilde{\varphi }= F_1(\widetilde{\theta },\widetilde{u})$, where $u=U(\varphi )$ or $u=U(\widetilde{\varphi })$, then $\varphi \le \widetilde{\varphi }$ a.e. in $\varOmega$.

Proof

Set $\overline{\theta }= \theta - \widetilde{\theta }$ and $\overline{\varphi }= \varphi - \widetilde{\varphi }$. Observe that Eq. (9) implies the equation

$$\begin{aligned} \alpha (\nabla \overline{\varphi },\nabla v) + \int _\varGamma [u(\varphi -\theta _b^4) - \widetilde{u}(\widetilde{\varphi }- \theta _b^4)]vd\varGamma +\kappa _a(\overline{\varphi }, v)= \kappa _a(|\theta |\theta ^3 - |\widetilde{\theta }|\widetilde{\theta }^3,v) \quad \forall v\in V. \end{aligned}$$

(11)

Denote $\psi = \max (\overline{\varphi }, 0)$ and put $v= \psi$ into (11) to obtain the estimate

$$ \alpha \Vert \nabla \psi \Vert ^2 + \int _\varGamma [u(\varphi -\theta _b^4) - \widetilde{u}(\widetilde{\varphi }- \theta _b^4)]\psi d\varGamma +\kappa _a\Vert \psi \Vert ^2=\kappa _a(|\theta |\theta ^3 - |\widetilde{\theta }|\widetilde{\theta }^3,\psi )\le 0. $$

Notice that the equality

$$ u(\varphi -\theta _b^4) - \widetilde{u}(\widetilde{\varphi }- \theta _b^4) = \widetilde{u}\overline{\varphi }+ (u - \widetilde{u})(\varphi - \theta _b^4) = u\overline{\varphi }+ (u - \widetilde{u})(\widetilde{\varphi }- \theta _b^4) $$

implies the non-negativity of the boundary integral in the estimate provided that $u=U(\varphi )$ or $u=U(\widetilde{\varphi })$. Therefore, $\psi = 0$, i.e. $\varphi \le \widetilde{\varphi }$ a.e. in $\varOmega$.

Theorem 2

In order for a function $u \in U_{ad}$ to be a strong minimizing optimal control, it is sufficient that $u=U(\varphi )$, where $\varphi = \varphi (u)$ is a solution of system (1)–(3) with the control u.

Proof

Assume that u satisfies the conditions of Theorem 2. Let $\widetilde{u} \in U_{ad}$ be an arbitrary control, $\theta = \theta (u)$, $\varphi = \varphi (u)$, $\widetilde{\theta }= \theta (\widetilde{u})$, and $\widetilde{\varphi }= \varphi (\widetilde{u})$. Lemma 1 implies the inequality $\varphi =F_1(\theta , u) \le F_1(\theta , \widetilde{u})=\widetilde{\varphi }_1$. Let

$$\begin{aligned} \widetilde{\theta }_k=F_2(\widetilde{\varphi }_k),\;\;\widetilde{\varphi }_{k+1}=F_1(\widetilde{\theta }_k,\widetilde{u}),\;\;k=1,2,\ldots . \end{aligned}$$

(12)

Since $\{\theta ,\varphi \}$ is a solution pair, the equation $\theta =F_2(\varphi )$ holds, and therefore, due to above mentioned properties 1 and 2 of the operators $F_1$ and $F_2$, the following inequalities are true:

$$ 0\le \theta \le \widetilde{\theta }_k\le M, \;\; 0\le \varphi \le \widetilde{\varphi }_k\le M^4,\;\; k=1,2,\ldots . $$

Notice that the sequences $\{\widetilde{\theta }_k\}$ and $\{\widetilde{\varphi }_k\}$ are bounded in V. Therefore, there exist functions $\theta _*,\,\varphi _*\in L^{\infty }(\varOmega )\cap H^1(\varOmega )$ such that

$$\begin{aligned} \widetilde{\theta }_k\rightarrow \theta _*,\;\; \widetilde{\varphi }_k\rightarrow \varphi _* \text { a.e. in } \varOmega ,\; \text { weakly in } H^1(\varOmega ),\; \text { and strongly in } L^2(\varOmega ) \end{aligned}$$

up to subsequences.

The above convergence allows us to pass to the limit in (12) as $k\rightarrow \infty$. Therefore, $\{\theta _*,\,\varphi _*\}$ is a weak solution of the problem (1)–(3) with the control $\widetilde{u}$. Moreover, $\theta \le \theta _*$ and $\varphi \le \varphi _*$. By the uniqueness of solutions of the problem (1)–(3), it holds that $\widetilde{\theta }=\theta _*$ and $\widetilde{\varphi }=\varphi _*$, and therefore $\theta \le \widetilde{\theta }$ and $\varphi \le \widetilde{\varphi }$, a.e. in $\varOmega$. This proves the theorem.

The proof of the next theorem is similar to that of Theorem 2.

Theorem 3

In order for a function $u \in U_{ad}$ to be a strong maximizing optimal control, it is sufficient that

$$ u(s) = {\left\{ \begin{array}{ll} u_1(s), &{} \text {if }\varphi (s) - \theta _b^4(s) > 0,\\ u_2(s), &{} \text {if }\varphi (s) - \theta _b^4(s) < 0, \end{array}\right. } $$

where $\varphi = \varphi (u)$.

Theorem 4

Let u and $\widetilde{u}$ be two strong optimal controls. Then $u= \widetilde{u}$ on $\varGamma$ where $\varphi \ne \theta _b^4$.

Proof

Let u and $\widetilde{u}$ be two strong optimal controls. From the definition of strong optimal controls, it follows that $\varphi (u) = \varphi (\widetilde{u}) = \varphi$ and $\theta (u) = \theta (\widetilde{u}) = \theta$, a.e. in $\varOmega$. Using Eq. (11) yields the relation

$$ \int _\varGamma [u(\varphi -\theta _b^4) - \widetilde{u}(\varphi - \theta _b^4)]vd\varGamma = \int _\varGamma (u - \widetilde{u})(\varphi - \theta _b^4) v = 0 \;\; \forall v \in V, $$

which yields that $(u - \widetilde{u})(\varphi - \theta _b^4) = 0$ a.e. in $\varGamma$. Therefore, $u = \widetilde{u}$ at points of $\varGamma$ where $\varphi \ne \theta _b^4$.

Corollary 1

If a strong optimal control $\widehat{u}$ is arbitrarily changed at points of $\varGamma$ where $\varphi (\widehat{u}) = \theta _b^4$, then it remains to be a strong optimal control.

Proof

Let $\widehat{u}$ be a strong optimal control, and $\widehat{\theta }$ and $\widehat{\varphi }$ the corresponding solutions satisfying Eqs. (4) and (5). Assume that $\widehat{u}$ is changed on the set $\{s\in \varGamma :\widehat{\varphi }- \theta _b^4=0\}$ to obtain a new control $\widehat{u}_{\mathrm {new}}$. Equations (4) and (5) imply that the pair $\{\widehat{\theta }, \widehat{\varphi }\}$ is also a weak solution corresponding to the modified control $\widehat{u}_{\mathrm {new}}$ because the last integral of Eq. (5) remains unchanged. Thus, the control $\widehat{u}_{\mathrm {new}}$ is a strong optimal control.

5 Iterative Algorithm for Finding the Optimal Control

By Theorem 2, a function $u \in U_{ad}$ such that $u=U(\varphi (u))$ is a strong minimizing optimal control. This gives rise to the idea to use an iterative procedure for finding strong minimizing optimal controls. Below, such a procedure will be proposed, and its convergence will be proven. This additionally proves the existence of strong minimizing optimal controls. The case of strong maximizing optimal controls is treated analogously.

Let $w \in U_{ad}$, $\varphi _0=\varphi (w)$, $\theta _0=\theta (w)$, i.e. $\varphi _0=F_1(\theta _0,w)$, $\theta _0=F_2(\varphi _0)$. Define the sequences

$$\begin{aligned} u_{k+1}=U(\varphi _k), \;\; \theta _{k+1}=F_2(\varphi _k),\;\;\varphi _{k+1}=F_1(\theta _{k+1},u_{k+1}),\;\; k=0,1,2,\ldots . \end{aligned}$$

(13)

Using properties 1 and 2 of the operators $F_1$ and $F_2$ yields the following estimates:

$$ 0\le \theta _k\le M, \;\; 0\le \varphi _k\le M^4,\;\; k=0,1,2,\ldots , $$

and, additionally, the sequences $\{\theta _k\}$ and $\{\varphi _k\}$ are bounded in V. Observe that $\theta _1=F_2(\varphi _0)=\theta _0$, and hence $\varphi _1=F_1(\theta _1,U(\varphi _0))\le \varphi _0=F_1(\theta _0,w)$ by Lemma 1. Then, the monotonicity of $F_2$ yields the inequality $\theta _2\le \theta _1$.

Now, inductive arguments yield the following relations:

$$\varphi _k\le \varphi _{k-1},\quad \theta _{k+1}\le \theta _k,\quad u_{k+1}\le u_k, \text { a.e. pointwise}, \text { for all } k\ge 1.$$

Indeed, if $\varphi _k\le \varphi _{k-1}$ and $\theta _{k+1}\le \theta _k$ for some $k\ge 1$, then, by the Lemma 1,

$$ \varphi _{k+1}=F_1(\theta _{k+1},U(\varphi _k))\le \varphi _k=F_1(\theta _k,u_k), $$

and therefore $\theta _{k+2}\le \theta _{k+1}$. Moreover, the monotonicity of the mapping U with respect to the a.e. pointwise order yields the inequality $u_{k+1}=U(\varphi _k)\le U(\varphi _{k-1})=u_k.$

Similar to the arguments used in the proof of Theorem 2, the properties of boundedness and monotonicity of the sequences $\{u_k\},\{\theta _k\}$, and $\{\varphi _k\}$ allow us to clime the existence of functions $\widehat{u}\in L^{\infty }(\varGamma )$ and $\widehat{\theta }$, $\widehat{\varphi }\in L^{\infty }(\varOmega )\cap H^1(\varOmega )$ such that

$$\begin{aligned} \begin{aligned}&u_k\rightarrow \widehat{u}\text { a.e. in }\varGamma ,\;\;\theta _k\rightarrow \widehat{\theta },\;\; \varphi _k\rightarrow \widehat{\varphi }\text { a.e. in }\varOmega ,\;\\&\text {weakly in }H^1(\varOmega ),\; \text { and strongly in }L^2(\varOmega ). \end{aligned} \end{aligned}$$

(14)

The convergence (14), taking into account the upper semi-continuity of the mapping U, allows us to pass to the limit in (13) to obtain the equations

$$ \widehat{u}=U(\widehat{\varphi }), \;\; \widehat{\theta }=F_2(\widehat{\varphi }),\;\;\widehat{\varphi }= F_1(\widehat{\theta },\widehat{u}). $$

Therefore, $\widehat{u}=U(\varphi (\widehat{u}))$, $\widehat{\theta }\le \theta (w)$, and $\widehat{\varphi }\le \varphi (w)$, i.e. $\widehat{u}$ is a strong minimizing optimal control.

Thus, the following statement is true:

Theorem 5

There exists a strong minimizing (resp. maximizing) control u uniquely defined on the set $\varGamma \setminus \{\eta \in \varGamma : \; \varphi (u) = \theta _b^4\}$. The modification of such a control on the set $\{\eta \in \varGamma : \; \varphi (u) = \theta _b^4\}$ does not violate its strong optimality.

6 Numerical Experiment

The following data are used in the numerical experiments. The region $\varOmega$ being a channel of the following form (the units are centimeters):

$$ \varOmega = \{r=(x_1, x_2, x_3): \; 0< x_2< 50, \; 0< x_{1,3} < 10 \}. $$

Fig. 1.

Distribution of the control on the top face, $x_3=10$, of the channel.

The boundary parts at $x_2= 0$ and $x_2= 50$ are inflow and outflow regions, respectively. The side faces, parallel to the $x_2$ axis, are solid walls of the channel. The velocity field is specified as $\mathbf v = (0,9,0)$ [cm/s]. The function $\theta _b$ is defined as follows:

$$ \theta _b(x_1,0,x_3)=0.5, \;\; \theta _b(x_1,50,x_3)=1, $$

$$ \theta _b(0,x_2,x_3)=\theta _b(10,x_2,x_3)=\theta _b(x_1,x_2,0)=\theta _b(x_1,x_2,10)=0.5 + 0.01 x_2. $$

The thermodynamical characteristics of the medium inside the channel correspond to air at the normal atmospheric pressure and the temperature of $400\,^\circ \mathrm {C}$. The maximum temperature in unnormalized model is chosen as $T_{max}=500\,^\circ \mathrm {C}$. The extinction coefficient $\kappa$ is equal to 0.1 [cm$^{-1}$], $\alpha = 3.3(3)$, the absorption coefficient $\kappa _a$ equals 0.01 [cm$^{-1}$], the anisotropy coefficient A equals 0, and the coefficient $\gamma$ equals 10.

It is assumed that the control u is variable on the upper face, $x_3= 10$, and constrained by the inequalities $0.2 \le u \le 0.4$. On the other faces, the control assumes prescribed constant values as follows:

$$ u(x_1,0,x_3)= u(x_1,50,x_3)= 0.5, $$

$$ u(0,x_2,x_3)=u(10,x_2,x_3)=u(x_1,x_2,0)= 0.3. $$

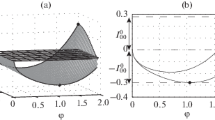
The iterative algorithm requires only two steps to deliver a strong maximizing optimal control. The distribution of this control on the upper face of the channel is shown in Fig. 1.

7 Conclusion

The current paper deals with a nonstandard problem of optimal control and proposes its complete solution. The notion of strong optimal controls seems to be a little bit unrealistic for common control problems. Nevertheless, the model considered in this work does have such solutions. They are unique in some sense and can be easily computed. Another surprising point is that the intuition fails when predicts that e.g. a strong maximizing optimal control should assume possibly maximal admissible values. In contrast to that, the example presented shows the opposite. Some analysis shows that a strong maximizing optimal control assumes minimal admissible values on a part of the surface where the absorption of thermal radiation occurs. Thus, the structure of strong optimal controls may be rather complicated, and therefore some practical heuristic solutions can be improved using the study presented. It would be also interesting to find other problems permitting strong optimal controls.