Fractional Factorial Experiments

Abstract

When there are numerous treatment factors to be examined but a limited budget, it may only be possible to observe a small proportion of the treatment combinations. Some main-effect and interaction contrasts cannot then be distinguished and are said to be aliased. Such fractional factorial experiments form the topic of in this chapter 15, where two methods of design construction are discussed to enable minimum aliasing between important contrasts. The first method is to select one block from a single-replicate block design. The second method uses the concept of an orthogonal array. Saturated designs, supersaturated designs, and definitive screening designs are introduced for searching for influential factors among a large number of potentially important factors. The concepts introduced in this chapter are illustrated through a real experiment and with the use of SAS and R software

Exercises

• 1. Decontamination experiment—beta particles, continued

  Suppose that only the first block of the data (beta particles) had been obtained in the decontamination experiment described in Exercise 8 of Chap. 13 (p. 466). The design would then have been a $\frac{1}{2}$-fraction of a $2^4$ experiment with defining relation $I={{ ABCD}}$. The half fraction is shown in Table 15.49. Analyze the data and compare your conclusions with those of the full experiment in Exercise 8 of Chap. 13. Explain the circumstances under which a half fraction would be preferred to a single-replicate factorial experiment.

  Table 15.49 Block I of the decontamination experiment

• 2. Mangold experiment, continued

  The mangold experiment in Sect. 13.5, p. 447, was a single replicate confounded design for a $2^5$ experiment in $b=4$ blocks of size 8. The five factors were Sulphate of Ammonia (factor A at levels 0 or 0.6 cwt per acre), Superphosphate (factor B at levels 0 or 0.5 cwt per acre), Muriate of Potash (factor C at levels 0 or 1.0 cwt per acre), Agricultural Salt (factor D at levels 0 or 5 cwt per acre), and Dung (factor E at levels 0 or 10 tons per acre). All of the 3-, 4-, and 5-factor interactions were expected to be negligible. The two three-factor interactions ${{ ABD}}$, ${{ BCE}}$ and their product ${{ ACDE}}$ were selected for confounding.

  Suppose that the data from only the third block had been available, so that we have a $\frac{1}{4}$-fraction. The data are reproduced in Table 15.50.

  • (a) Write down the aliasing scheme for this fractional factorial experiment.

  • (b) Analyze the data. What conclusions can you draw?

  • (c) Comparing your conclusions with those of Sect. 13.5, what extra information do you gain by running the single-replicate design instead of the fraction?

  • (d) When would you recommend that an experimenter consider using a fractional factorial design rather than a single-replicate design?

Table 15.50 Yields (in pounds) of mangold roots for Block III of the mangold experiment

Table 15.51 Volume of dyestuff for Block I of the dye experiment

• 3. Dye experiment, continued

  The dye experiment was discussed in Sect. 14.2.4 (p. 478). There were three factors: the concentration of inorganic material M in the free water in the reaction mixture (factor A at three equally spaced levels), the volume of free water in the reaction mixture (factor B at three equally spaced levels), and the concentration of inorganic material N in the free water in the reaction mixture (factor C at three equally spaced levels). The data for the first replicate of the original experiment were given in Table 14.6 (p. 479) and the first block is reproduced in Table 15.51. The design for the first replicate was a single-replicate design that confounded (${{ AB}}^2{\!}C^2$; $A^2{\!}{{ BC}}$). Analyze the data of Block I as though it had come from a $\frac{1}{3}$-fraction. State your conclusions.

• 4. Sugar beet experiment, continued

  The sugar beet experiment described in Exercise 6 of Chap. 14 concerned the effects of three standard fertilizers, nitrogen, phosphate, and potassium (factors N, P, and K), each at three equally spaced levels, on sugar beet yield. The experiment was run as a single-replicate confounding the contrasts (${{ NP}}^2{\!}K$; $N^2{{ PK}}^2$). Suppose the only data available were those of Block III, reproduced in Table 15.52.

  • (a) If the only data available were those from Block III, write out the aliasing scheme for the design.

  • (b) Analyze the data from Block III as though they came from a $\frac{1}{3}$-fraction. State your conclusions.

• 5. Flour experiment, continued

  Suppose that the data from Block II of the $4\times 2^4$ experiment in Table 15.16 (p. 514) had been lost, so that only Block I remained. This would then constitute a $\frac{1}{4}$-fraction.

  • (a) Write out the aliasing scheme for the design. What is the resolution number. Is this a good design?

  • (b) Bearing in mind the purpose of the experiment, can you find a better $\frac{1}{4}$-fraction? If so, write out the design and its aliasing scheme.

  • (c) Analyze the data from Block I of Table 15.16. What can you conclude?

• 6. Handwheel experiment

  E.N. Corlett and G. Gregory describe an experiment in the 1960 issue of Applied Statistics that was concerned with finding the design of a machine tool handwheel that would maximize the accuracy on the part of the operator in the setting of the machine tool handwheel. The apparatus consisted of an optical dividing head with a dial mounted onto a mandrel to which was connected the handwheel spindle. The spindle was provided with an adjustable friction brake. The operator first offset the dial by $15^\circ$ and then moved the handwheel so that a line on the dial was brought “into coincidence with a fixed line on the dividing head, making the final adjustment by means of a series of taps by hand on the handwheel rim.”

  Seven factors, each at two levels (coded 0 and 1) were investigated as follows.

Table 15.52 Yields of sugar beet for Block III of the sugar-beet experiment

Table 15.53 Log variance of observations for the handwheel experiment

A::

Handwheel diameter (5.5 in., 10 in.)

B::

Dial diameter (4 in., 8 in.)

C::

Thickness of the dial line (0.008 in., 0.064 in.)

D::

Friction of the spindle (7.5 lb.-in., 45 lb.-in.)

E::

Level of operator’s elbow relative to height of handwheel

(Level with center of spindle, 6 in. above spindle center)

F::

Previous experience of operator (Practiced, Nonpracticed)

G::

Knowledge of accuracy of previous setting (Feedback, No feedback)

• The response variable was $\ln (s^2)$, where $s^2$ was the sample variance of 25 repeated observations for a particular treatment combination. It was estimated that each set of 25 repeated observations would take about 15 min to complete, including setup time. In a morning or afternoon session of four hours, therefore, sixteen observations could be taken. The experiment was to last over two days, which meant that a $2^{7-1}$ fractional factorial experiment was required, divided into 4 blocks of 16.

• The highest-order interaction was selected for the defining relation of the fraction, that is, $I = {{ ABCDEFG}}$. Only two operators were used for the experiment, one for each level of practice. The difference between these operators was not of interest, only the interaction of the level of practice with the other factors. Rather unusually, then, the main effect of F was selected as one of the contrasts for confounding. All the 2-factor interactions and most of the 3-factor interactions were thought to be of interest. Unlikely 3-factor interactions included ${{ ACG}}$ and ${{ BDE}}$, which were also chosen for confounding with blocks. The complete set of confounded contrasts was F, ${{ ACG}}$, ${{ ACFG}}$ together with its set of aliases ${{ ABCDEG}}$, ${{ BDEF}}$, ${{ BDE}}$. All other main-effect, 2-factor, and 3-factor interaction contrasts could be estimated.

• The data obtained from the experiment are shown in Table 15.53.

• (a) Write out the aliasing scheme for the design.

• (b) Using a computer package, estimate the (estimable) main-effect and interaction contrasts.

• (c) Prepare a half-normal probability plot of the contrast estimates and identify the most important main effects and interactions.

• (d) The authors of the article point out that if the responses are normally distributed and n is large (where n is the number of repeated observations, 25 in this experiment), then the response variable ln$(s^2)$ has approximately constant variance equal to $2/(n-1)$. Calculate the standard error for each of the contrasts estimated in part (c). Using Bonferroni’s method with an individual significance level of 0.001 for each test (giving an overall level of at most 0.06), which main effects and interactions are significantly different from zero? Do these results agree with the results from part (c)? Discuss why or why not.

• (e) Draw interaction plots of the important interactions and discuss recommended settings for the six factors A, B, C, D, E, and G for the practiced and nonpracticed operators individually.

• (f) Would you recommend further experimentation? If so, which factors and which settings would you recommend? Can you suggest a suitable design?

• 7. Paint experiment

  • (a) Suppose that you need to design an experiment involving 6 factors (A, B, C, D, E, F) at 2 levels each (64 treatment combinations) and that only 8 observations can be taken. You decide to sacrifice information on the ${{ ABF}}$, ${{ ACDF}}$, and ${{ ABCE}}$ contrasts. Write out the defining relation and the two rows of the aliasing scheme showing the aliasing of A and the aliasing of ${{ AC}}$.

  • (b) Explain what aliasing means.

  • (c) An experiment was run in Germany by S. Eibl, U. Kess, F. Pukelsheim (Journal of Quality Technology, 1992) on the thickness of a paint coating. Prior to the experiment, the thickness achieved was around 2 mm, much higher than the target 0.8 mm. They selected the following six factors, each at two levels:

    

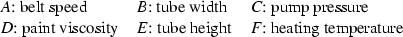
    They used the $\frac{1}{8}$-fraction with the aliasing scheme in part (a), and they decided to ignore all interactions for this first experiment. Since they wanted to monitor the variation of the thickness, they took four observations on each of the 8 treatment combinations in the fraction. The data are shown in Table 16.1, p. 570, where the two levels of each factor are coded as −1 and 1 and shown for factors A–F in the columns labeled $z_A$–$z_F$.

    Calculate the analysis of variance table and contrast estimates using response variable LNVAR (the log variance). What do you conclude?

  • (d) Assuming that the order of observations was completely randomized, calculate the analysis of variance table and also contrast estimates of interest, using the 32 observations separately (without combining them into an average). Remembering that the goal is to reduce the thickness, what conclusions would you draw from this particular experiment?

  • (e) The experimenters decided to run a followup experiment with at most 16 observations. You can use any of the original 6 factors and you can change the levels from their original settings. The ultimate goal is to achieve a coating of 0.8 mm. Suggest a followup experiment.

Table 15.54 $2^{10-6}$ resolution III fraction and pore diameter (nm) for the anatase experiment of Exercise 8

• 8. Anatase experiment

  R.E. Olsen and coauthors described several experiments in the Journal of Porous Materials (2014). concerned the study of anatase (a form of titanium dioxide) as a catalyst support. Specific catalyst support properties are required, such as certain surface area, pore volume, and pore diameter. Samples were prepared by mixing various chemicals with water in specified orders and speeds to produce a “slurry”. For half the observations, the slurry was (i) dried, (ii) rinsed with distilled water and (iii) calcinated; this was called the DRC procedure. For the remaining observations, (ii) and (iii) were interchanged to give the DCR procedure.

  In the first of their experiments, all factors had two levels, coded here as 0 or 1. These factors were A Mixing order, B speed of water addition (slow, fast), C amount of water (7 ml, 25 ml), D rinsing order (DRC, DCR), E drying time (3 h, 24 h), F drying temperature (25 $^\circ \mathrm{C}$, 100 $^\circ \mathrm{C}$), G calcination ramp rate (2 $^\circ \mathrm{C}$/min, 20 $^\circ \mathrm{C}$/min), H calcination temperature (400 $^\circ \mathrm{C}$, 700 $^\circ \mathrm{C}$), I calcination time (2 h, 20 h), J amount of an aluminium compound added (5, 22). A $2^{10-6}$ resolution III fraction was run. Several responses were measured, including the pore diameters which are listed together with the fraction in Table 15.54. The observations were taken in a random order (not shown here).

  • (a) Part of the aliasing scheme for the design is:

    $$ E=ACD,~F=BCD~, G=ACD,~H=CD,~I=ABCD,~J=ABC\,. $$

    Write out the defining relation for the fraction (a total of 63 contrasts):

  • (b) Fifteen factorial effects can be included in the model. This can include the 10 main effects. Suggest five interaction contrasts to include (these cannot be aliased with main effects nor with each other.)

  • (c) Estimate the 15 contrasts in your model and plot a half normal probability plot.

  • (d) From part (c), which factors seem to affect the pore diameter the most. Suppose you were going to follow up these factors and their interactions in more detail in a later experiment. How would you design such an experiment if you could take 16 observations?

• 9. Flour early experiment

  The flour experiment was introduced in Example 15.5.1, p. 513. In Table 15.55, we show part of the design for an early experiment (the first in a series of four experiments). Six ingredients, A, B, C, D, E, F, added to the flour were to be investigated in the experiment. In addition, there were three noise factors: Factor P (which was a combination of factors N and S in Example 15.5.1) had two levels (“high yeast with long proof time” or “low yeast with short proof time”), Factor Q, (as in Example 15.5.1, two levels “undermixing, little water, heavy pressure” or “overmixing, much water, little pressure”), and Factor R (two levels, underbake or overbake).

  A crossed array was selected. The noise array was a $\frac{1}{2}$-fraction with defining relation $I=PQR$. Each of the four noise combinations was run on a single day, so that the experiment ran over four days. The design array was a $\frac{1}{4}$-fraction with defining relation $I={{ ABCD}}={{ BCEF}}={{ ADEF}}$, and this was run on each day. Thus the noise contrasts are confounded with days and cannot be analyzed. However, the object of the experiment was to examine the average yield (specific volume, ml/100 g) and the variance of the yield for the design factors across the noise factors.

  • (a) Calculate the average yield and the log variance of the yield for each design-treatment combination.

  • (b) Analyze the two sets of data separately. What recommendations would you make if the objective is to reduce the variability and increase the specific volume?

Table 15.55 Specific volume for part of experiment 1 of the flour early experiment

• 10. Injection molding experiment

  S.R. Schmidt and R.G. Launsby in their book Understanding Industrial Designed Experiments describe an experiment on the effect of six factors on the shrinkage of a part produced by injection molding. The six factors were injection velocity (factor A), cooling time (factor B), barrel zone temperature (factor C), mold temperature (factor D), hold pressure (factor E), and back pressure (factor F). Each factor had two levels coded 0 and 1.

  There were two responses of interest, the length and width of the part after shrinkage. The purpose of the experiment was to find settings of the six variables that would enable the parts to be “on target,” that is, a post-shrinkage length of 14.5 units and width of 9.35 units.

  The orthogonal array in Table 15.22, p. 518, was selected with columns columns 1–6 labeled A, B, D, C, E, F, and columns 5 and 6 multiplied by $-1$. One degree of freedom (corresponding to column 7) is available to measure $\sigma ^2$ or one of the two-factor interactions. Five parts were measured at each treatment combination, and the lengths and widths are recorded in Table 15.56.

  • (a) Write down the defining relation for the $\frac{1}{8}$-fraction and the aliasing scheme. The investigators assumed that all the interactions were negligible. If they had not done so, which interactions could have been measured?

  • (b) For the length data, calculate the average response and the standard deviation of the response for each treatment combination.

  • (c) Can you recommend which factors should be investigated more thoroughly in order to find a setting that would give the required length and also factors that could be set to reduce the variability?

  • (d) Repeat parts (a) and (b) for the width data.

  • (e) Can you make any overall recommendation?

  • (f) Write down the assumptions on the model that would need to be true in order to interpret the analysis of variance. Are these assumptions likely to be valid for this experiment?

  Table 15.56 Lengths and widths of parts after shrinkage in the injection molding experiment

• 11. Spectrometer experiment, continued

  Read the details of the spectrometer experiment in Exercise 10 of Chap. 7. You will need to have access to your solutions to that exercise to answer this question.

  Suppose that you are consultant for a different company and that they wish to run a similar experiment, with the same five factors, but with a total of 64 observations. To keep things simple, you might recommend that factors A and C be examined at 2 levels each rather than 3 levels in your first experiment (even though you may suspect that some of the factors have quadratic trends). Thus, you have a $2^5$ experiment. List 5 interactions that you are particularly interested in studying. You should use information from your answer to (a) and (b) of Exercise 10 of Chap. 7 in choosing the interactions. Design a factorial experiment in 4 blocks of size 8. State exactly how you chose your design. Write out at least three of the treatment combinations in two of the blocks and explain how you obtained them.

• 12. Design of industrial experiment

  Suppose that you are asked to design an experiment for 6 treatment factors each having two levels. Only 64 observations can be taken in total, and these should be divided into 8 blocks of size 8. Suppose that you decide to confound the interaction contrasts ${{ ABD}}$, ${{ DEF}}$, and ${{ ACDF}}$.

  • (a) Can all the other interaction contrasts be estimated?

  • (b) What does the statement “${\!}{{ ABD}}$ is confounded” mean?

  • (c) How would you obtain the 8 blocks? Write out two blocks as an example.

  • (d) Suppose that the budget is cut before the experiment can take place, and only 8 observations can be taken in total. How would you decide which 8 observations to take? What can be estimated?

  • (e) Suppose that you were fairly sure that all interactions involving 4 factors or more were negligible and that neither D nor F interacts with any of the other factors. Suppose that the analysis of variance table obtained from the results of the experiment is as in Table 15.57. What would you investigate in a followup experiment? Give your reasons.

Table 15.57 Analysis of variance for the industrial experiment

• 13. Suppose that you wish to run an experiment with four treatment factors (A, B, C, D) each having three levels. The only likely interactions are ${{ AB}}$, ${{ AC}}$, and ${{ ABC}}$. The experiment needs to be run in blocks of size at most $k=9$.

  • (a) Design a $3^4$ experiment in $b=3^2$ blocks of size $k=3^2$ confounding ${{ ABD}}$ and ${{ AB}}^2{\!}{{ CD}}$. What else is confounded? Are you happy with this design? Why or why not?

  • (b) Show how you would obtain the nine blocks and show one of the blocks as an illustration.

  • (c) Write out the degrees of freedom column for the analysis of variance table. (Read the question information again before you do this.)

  • (d) Suppose that the blocks are randomly ordered. After the first block is run, the budget for the experiment is cut, so only nine observations are available. The design is now a $3^{4-2}$ fractional factorial design. Write down the defining relation for the design. Is this design going to be useful in examining the main effects and the interactions of interest? Why or why not?

  Table 15.58 Plackett–Burman design and data for Exercise 14

• 14. Plackett–Burman and supersaturated design

  Table 15.58 shows a hypothetical set of data from a Plackett–Burman design with 20 observations and 19 factors. The data were simulated from a model in which factors C, J, K and P all have large main effects, all other main effects are drawn from a N(0, 4.5) distribution and the random errors have a N(0, 3) distribution. There are no interactions.

  Table 15.59 Definitive screening design and pore diameter (nm) for the anatase experiment of Exercise 15

  • (a) Using the data from Table 15.58, either fit a full main effects model or run an all-subsets regression to verify that the four important factors can be detected.

  • (b) What are the estimates of the main effects of the four important factors?

  • (c) Using the first column of the design in Table 15.58 as a branching column, create a supersaturated design corresponding to $+1$ in the branching column.

  • (d) The supersaturated design in part (c) has 10 observations which may not be quite sufficient to be able to detect four large main effects. Run an all-subsets regression using the 10 observations. How many of the four important factors can be detected and what are their main effect estimates?

• 15. Anatase experiment

  The anatase experiment was described in Exercise 8. After the initial experiment, several further experiments were run. Table 15.59 shows one of the definitive screening designs (where factor D of Exercise 8 has been set at level DCR, and factor A held constant). The response shown is pore diameter (nm), The randomized order of the observations is shown in the original paper. The design allows linear and quadratic trends in the main effects of some factors and some of the linear$\times$linear interactions to be measured.

  Table 15.60 $2^{p-s}$ fractions of $2^p$ experiments. For each defining relation, s independent generators are underlined, and s corresponding equations are given. To obtain the $v=2^{p-s}$ treatment combinations in the fraction, list all v combinations of levels $a_i$ of the $p-s$ factors not determined by the equations, then use the equations modulo 2 to complete each treatment combination. For two blocks, confound the effect in parentheses and its aliases

  Table 15.61 $3^{p-s}$ fractions of $3^p$ experiments. For each defining relation, s independent generators are underlined, and s corresponding equations are given. To obtain the $v=3^{p-s}$ treatment combinations in the fraction, list all v combinations of levels $a_i$ of the $p-s$ factors not determined by the equations, then use the equations modulo 3 to complete each treatment combination

  • (a) Use an all subsets regression to find a model that explains much of the variability in the data ($R^2$ at least 0.90). Remember to include the main effects of any factors that are involved in large linear$\times$linear interactions.

  • (b) If you were to design a follow-up experiment, which factors (and interactions) would you examine? Suggest a suitable design if you could take 16 more observations.

Table 15.62 Orthogonal arrays with $2^p$ observations and useful column labelings. Assign factors in alphabetical order

Table 15.63 Generators for cyclically generated orthogonal main-effect plans. These are saturated designs for factors each at two levels, for n observations with n divisible by 4 but not a power of 2. To generate a design, systematically cycle the generator to the right to obtain $n-1$ rows; then include a final row of $-1$’s

Table 15.64 Orthogonal arrays for 18 observations: $L_{18}(3^6\times 6$) and $L_{18}(3^7\times 2)$

Table 15.65 A $3^p$ orthogonal array for 27 observations: $L_{27}(3^{13})$