Abstract
The aim of this chapter is to show how general relativity can be applied to some selected significant physical cases. The nature of this book prevents a detailed treatment of these and other important applications, which, however, can be found in many other places (see, e.g., Weinberg 1972 or Misner et al. 1973). Indeed, the rationale of these choices is not to give an extensive and complete overview of the applications of the Einsteinian theory of gravitation, but rather to provide a basis for the successive investigation of possible alternative theories, which is the next and final chapter of this work.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
It has to be not that in general the spherical symmetry condition just requires that the radius of curvature is a general function of a radial coordinate \(\rho \) and of the time t, so that \(\mathrm {d}s^{2}=f\left( \rho , t\right) \left( \mathrm {d}\theta ^{2}+\sin \theta \mathrm {d}\varphi ^{2}\right) \), but we can drop the time dependence because of the assumption of a static solution. Moreover, the choice of the radial coordinate is somewhat arbitrary, and having put \(f\left( \rho \right) =r^{2}\) we have simply selected the coordinate that makes the hypersurfaces of constant radius have an area of \(4\pi r^{2}\).
- 2.
That is, the Lagrangian does not depend on t and \(\varphi \).
- 3.
For example, \(3{ GM}/c^{2}\simeq 4.5\) km in the case of the sun. Because we are dealing with an exterior solution, only the orbits outside the physical dimensions of the body can be treated by this metric, so these 4.5 km have to be compared with the radius of the sun \(R\simeq 7\cdot 10^{5}\) km.
- 4.
It can be easily understood also by noting that Eq. (9.1.13) becomes \(u''+u=0\) for \(M=0\).
- 5.
Which however is not strictly related to general relativity because it is a general consequence of the equivalence Principle.
- 6.
For the same reason this method is preferred here over the derivation of the linearized field equations from the variation of the linearized Einstein–Hilbert action.
- 7.
Remembering that the d’Alembert operator is defined as
 .
. - 8.
In electrodynamics the gauge transformation for the four-potential reads \(\bar{A}^{\alpha }=A^{\alpha }-\partial ^{\alpha }\chi \), which is the counterpart of Eq. (9.2.6). This can be more easily understood if we define the so-called transverse-traceless perturbation
$$ \bar{h}_{\alpha \beta }\equiv h_{\alpha \beta }-\frac{1}{2}\eta _{\alpha \beta }h, $$where \(h=\eta ^{\gamma \delta }h_{\gamma \delta }\). Similarly, the Lorenz gauge \(\partial _{\alpha }\bar{A}^{\alpha }=0\) gives the field equations in the form
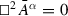 . This resembles that of Eq. (9.2.7), which in terms of the transverse-traceless perturbation reads \(\partial _{\alpha }\bar{h}^{\alpha \beta }=0\).
. This resembles that of Eq. (9.2.7), which in terms of the transverse-traceless perturbation reads \(\partial _{\alpha }\bar{h}^{\alpha \beta }=0\). - 9.
Because in this context it is customary to use the symbol \(\varPhi \) for another potential, we use U for the Newtonian gravitational potential.
- 10.
The cited work of Chandrasekhar, however, uses a different convention for the signature of the metric tensor.
- 11.
Such argument was considered since the early advent of Newtonian gravity by the theologian and scholar an Richard Bentley and exposed in mathematical detail by Hugo Seeliger at the end of the nineteenth century.
- 12.
With this expression one can reasonably mean scales of the order of 100 Mpc.
- 13.
At least as long as it is a metric theory of gravity.
- 14.
The geometry on the surface of a sphere can be studied as a function of its two-dimensional coordinates only. This means that one can define the intrinsic geometric properties of a manifold using measures of angles, lengths, and areas completely defined within the manifold itself, i.e., without considering it embedded in a space with more dimensions. The first generic and comprehensive systematization of such technique was done by Carl Friedrich Gauss in the first half of the nineteenth century.
- 15.
The homogeneity of space implies that we can consider any point as the origin of the spatial coordinates with no influence on the distance measurements.
- 16.
This is true even beyond the expectations. Indeed, the fact that the assumptions of the homogeneity and isotropy of space(-time) fit perfectly in a Euclidean geometry, has the even more noticeable consequence that everything we derived above, and everything be shown in the following can be devised in the framework of Newton’s theory of gravity, as first proved by Milne (1934) and McCrea and Milne (1934). In particular we obtain very similar results by assuming the constancy of the speed of light, hence showing that the problems of Newtonian cosmology rather came from the additional assumption of an infinite and static universe. An in-depth and brilliant exposition of these considerations can be found in Bondi (1961).
- 17.
Basically, this is due to the homogeneity and isotropy hypothesis.
- 18.
We can interpret the word “cosmological” as “global”. The scale factor specifies the geometry of the overall universe “as a whole”, once the type of geometry, i.e., the value of k, is set.
- 19.
As pointed out in Appendix C.4.1, in cosmology dust (also called matter) and radiation are both particular cases of a perfect fluid. Here we can see that the characterization given by the equation of state coincides with the definition of dust used there.
- 20.
In convenient units of measure where \(F_{\mathrm {r}}=1\).
- 21.
Remember that here we set the unit of measures in such a way that \(c=1\).
- 22.
We can consider with no loss of generality the case with \(\varphi _{0}=0\).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
Vecchiato, A. (2017). Applications. In: Variational Approach to Gravity Field Theories. Undergraduate Lecture Notes in Physics. Springer, Cham. https://doi.org/10.1007/978-3-319-51211-2_9
Download citation
DOI: https://doi.org/10.1007/978-3-319-51211-2_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-51209-9
Online ISBN: 978-3-319-51211-2
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


 .
.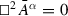 . This resembles that of Eq. (
. This resembles that of Eq. (