Determining Wide-Area Signals and Locations of Regulating Devices to Damp Inter-Area Oscillations Through Eigenvalue Sensitivity Analysis Using DIgSILENT Programming Language

Abstract

This chapter introduces the concept of eigenvalue sensitivity to analyse the installation location and feedback signals of damping regulating devices using DIgSILENT Programming Language. A state-space representation of the linearized system is estimated by dynamic simulations and used to provide two indices based on mode controllability and mode observability. By inspection of these indices, the number of location/signal candidates is reduced, decreasing the computational cost of modal analysis and time-domain simulation for the final selection of regulating device location and feedback signals. This approach is applied to determine the location/signal of a Battery Energy Storage (BES) regulating the inter-area oscillation between the Northern Chile Interconnected System (NCIS) and the Argentinian Interconnected System (AIS).

The original version of this chapter was revised: ESM files have been included. The erratum to this chapter is available at https://doi.org/10.1007/978-3-319-50532-9_15

7.1 Introduction

Smart grids take advantage of communication technologies and computer-based remote control and automatization over a wide range of power system devices such as breakers, capacitors, transformers and even Flexible Alternate Current Transmission Systems (FACTS) and Energy Storage Systems (ESS). In particular, FACTS and ESS may play an important role as damping regulating devices in the control of inter-area oscillations, which are expected to appear more frequently in the system as a consequence of a relative system inertia reduction.

These damping regulating devices have the advantage to be installed virtually anywhere in the power system, allowing better performances in comparison with Power System Stabilizers (PSS)—which may work well for local rather than inter-area oscillations. Therefore, installation location can be determined as a design parameter when considering system dynamics [1]. Also, wide-area measurements as feedback signals for the controllers are proven to have a positive impact on the performance [2, 3]. Thus, feedback signals may be considered as a design parameter choosing from available measurements coming from Phasor Measurement Units (PMU) or similar devices. Although a common analysis, exhaustive time-domain simulations over all the possible locations and signal candidates are computationally expensive and unfeasible for real power systems. Hence, an analytical approach is desired.

A screening approach based on eigenvalue sensitivity allows comparing the impact of damping regulating devices for different installation locations and different feedback signals, using a state-space representation of the linearized system under study. The best location/signal candidates are chosen, and for final selection, time-domain simulations using the nonlinear system model are executed. This chapter employs the concept of eigenvalue sensitivity and defines metrics to compare the effects of the location and measurements candidates on the oscillation damping. The approach is coded in DIgSILENT Programming Language and applied to decide the location/signals of a Battery Energy Storage System (BESS) in the Northern Chile Interconnected System (NCIS) when connected to the Argentinian Interconnected System (AIS).

7.2 Eigenvalue Sensitivity

7.2.1 General System Representation

Power systems are large-scale nonlinear systems with complex dynamics and parameter dependencies. In the case of low-frequency oscillations, a recurrent phenomenon in power systems, the dynamics can be fairly represented by a linearized representation around a given equilibrium point. In mathematical form:

$$ \Delta \dot{x} = A\Delta x + B\Delta u $$

(7.1)

$$ \Delta y = C\Delta x + D\Delta u $$

(7.2)

where $\Delta x = x - x^{e}$, $\Delta y = y - y^{e}$ and $\Delta u = u - u^{e}$. Here, x, y and u correspond to the vectors of state, output and input variables, respectively—the superscript e indicates that the variables are those at the equilibrium point. A, B, C and D are the system matrices—all with proper dimensions. The zero-input response of this system for each state variable $\Delta x_{j} \left( t \right)$ can be expressed as shown by Pizarro-Gálvez et al. [4] as:

$$ \Delta x_{j} \left( t \right) = \mathop \sum \limits_{i = 1}^{n} k_{ji} {\text{e}}^{{\lambda_{i} \left( {t - t_{0} } \right)}} , \forall t \ge t_{0} $$

(7.3)

where $\lambda_{i}$ is the $i{\text{th}}$ system eigenvalue and k _ji is a corresponding constant. The term ${\text{e}}^{{\lambda i\left( {t - t0} \right)}}$ is the $i{\text{th}}$ system mode. When the eigenvalue is a complex number such as $\lambda_{i} = \alpha_{i} + j\beta_{i}$, the mode corresponds to an oscillation of the form ${\text{e}}^{{\upalpha_{i(t - t0)} }} {\text{e}}^{{j\upbeta_{{i\text{(}t - t0\text{)}}} }}$. From here, the concepts of damping, oscillation frequency and structural stability can be defined—check Refs. [4, 5].

7.2.2 Eigenvalue Problem and Parameter Dependency

The eigenvalue problem can be stated as:

$$ \left( {A - \lambda_{i} I} \right)v_{i} = 0 $$

(7.4)

$$ \omega_{i}^{T} \left( {A - \lambda_{i} I} \right) = 0 $$

(7.5)

where v _i and ω _i are the right and left eigenvectors associated with the ith eigenvalue λ _i . Note that the matrix A is dependent on the system parameters, which are assumed to be constant during dynamic simulation. When these parameters change, the system matrix A is modified, and consequently, the original eigenvalues and eigenvectors are affected. As an example, consider the gain of a feedback loop controller. The change of this parameter can potentially displace a critical eigenvalue of interest; if the displacement is towards the negative direction of the real axis, a desire damping ratio may be achieved, or if the displacement is towards the positive direction, the damping ratio would be reduced in such a way that the eigenvalue may even cross the imaginary axis making the system unstable. Another interesting example is when, out of different potential actuators, the most effective one to displace critical eigenvalues needs to be chosen. In the same line of thoughts, the actuator signal can be selected; out of several system signals, which signal would be the most effective to displace the critical eigenvalue? To answer these questions, the study of eigenvalue sensitivity under system parameters is crucial and will be addressed next.

Consider the eigenvalue problem again shown in (7.4) and differentiate this with respect to a generic parameter K as follows:

$$ \frac{\partial }{\partial K}\left\{ {\left( {A - \lambda I} \right)v_{i} } \right\} = \left( {A - \lambda_{i} I} \right)\frac{{\partial v_{i} }}{\partial K} + \left( {\frac{\partial A}{\partial K} - \frac{{\partial \lambda_{i} }}{\partial K} I} \right)v_{i} = 0 $$

(7.6)

Pre-multiplying (7.6) by the $i{\text{th}}$ left eigenvector $\omega_{i}^{T}$ and assuming that the eigenvectors are normalized, i.e. $\omega_{i}^{T} v_{i} = 1$, the following relationship is obtained:

$$ \underbrace {{\omega_{i}^{T} \left( {A - \lambda_{i} I} \right)}}_{0}\frac{{{\partial }v_{i} }}{{{\partial }K}} + \omega_{i}^{T} \frac{\partial A}{\partial K}v_{i} - \underbrace {{\omega_{i}^{T} v_{i} }}_{1}\frac{{{\partial }\lambda_{i} }}{{{\partial }K}} = 0 $$

(7.7)

$$ \Rightarrow \frac{{\partial \lambda_{i} }}{\partial K} = \omega_{i}^{T} \frac{\partial A}{\partial K}v_{i} $$

(7.8)

7.2.3 Mode Controllability and Mode Observability

The well-known expression obtained in the previous section is useful to determine the eigenvalue sensitivity; however, it is not practical in a multi-parameter analysis, since the calculation of the derivative of the matrix A with respect to the parameter K is required. Therefore, a simpler relationship with a more affordable term is needed. The following approach gives an equivalent representation of Eq. (7.8) for a more generic feedback control considering only calculations derived from the original system matrices and the feedback transfer function. Finally, this expression will be generalized to introduce two main factors of the eigenvalue sensitivity: mode controllability and mode observability.

Consider a generic system “a” with an output feedback controller called system “b.” Note that while the controller output (y _b ) is the system input (u _a ), the controller input (u_b) is the system output (y _a ). The state-space representation is:

$$ \dot{x}_{a} = A_{a} x_{a} + B_{a} y_{b} $$

(7.9)

$$ y_{a} = C_{a} x_{a} $$

(7.10)

$$ \dot{x}_{b} = A_{b} x_{b} + B_{b} y_{a} $$

(7.11)

$$ y_{b} = C_{b} x_{b} + D_{b} y_{a} $$

(7.12)

Alternatively, in compact matrix form:

$$ \left[ {\begin{array}{*{20}l} {\dot{x}_{a} } \hfill \\ {\dot{x}_{b} } \hfill \\ \end{array} } \right] = \underbrace {{\left[ {\begin{array}{*{20}l} {A_{a} + B_{a} D_{b} C_{a} } \hfill & {B_{a} C_{b} } \hfill \\ {B_{b} C_{a} } \hfill & {A_{b} } \hfill \\ \end{array} } \right]}}_{A}\left[ {\begin{array}{*{20}l} {x_{a} } \hfill \\ {x_{b} } \hfill \\ \end{array} } \right] $$

(7.13)

The matrix A is the closed loop system matrix. Note that, in frequency domain, the controller transfer function can be compactly written as:

$$ H\left( s \right) = C_{b} M_{b} \left( s \right)B_{b} + D_{b} $$

(7.14)

where

$$ M_{b} \left( s \right) = \left( {sI - A_{b} } \right)^{ - 1} $$

(7.15)

Moreover, the derivative of H(s) with respect to the controller in K is denoted as H′(s) and has the following expression:

$$ \begin{aligned} H^{\prime}\left( s \right) = & C_{b}^{\prime} M_{b} B_{b} + C_{b} M_{b}^{\prime} B_{b} + C_{b} M_{b} B_{b}^{\prime} + D_{b}^{\prime} + C_{b}^{\prime} M_{b} B_{b} \\ & \quad + C_{b} M_{b} A_{b}^{\prime} M_{b} B_{b} + C_{b} M_{b} B_{b}^{\prime} + D_{b}^{\prime} \\ \end{aligned} $$

(7.16)

Note that the augmented left and right eigenvector satisfies (7.4) and (7.5), thus,

$$ \left[ {\begin{array}{*{20}c} {A_{a} + B_{a} D_{b} C_{a} } & {B_{a} C_{b} } \\ {B_{b} C_{a} } & {A_{b} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {v_{i1} } \\ {v_{i2} } \\ \end{array} } \right] = \lambda_{i} \left[ {\begin{array}{*{20}c} {v_{i1} } \\ {v_{i2} } \\ \end{array} } \right] $$

(7.17)

$$ [\omega_{i1}^{T} \omega_{i2}^{T} ]\left[ {\begin{array}{*{20}c} {A_{a} + B_{a} D_{b} C_{a} } & {B_{a} C_{b} } \\ {B_{b} C_{a} } & {A_{b} } \\ \end{array} } \right] = \lambda_{i} [\omega_{i1}^{T} \omega_{i2}^{T} ] $$

(7.18)

If v_i1 is the right eigenvector of the open loop system, then $v_{i2} = M(\lambda_{i} )B_{b} C_{a} v_{i}$. Similarly, assuming $\omega_{i1}^{T}$ is the left eigenvector of the open loop system, then $\omega_{i2}^{T} = \omega_{i}^{T} B_{a} C_{b} M(\lambda_{i} )$.

Finally, by Eq. (7.8), the sensitivity of a closed loop system eigenvalue with respect to the controller gain K is given by:

$$ \lambda^{\prime} = \frac{{\partial \lambda_{i} }}{\partial K} = \omega_{i}^{T} \frac{\partial A}{\partial K}v_{i} = [\omega_{i1}^{T} \omega_{i2}^{T} ]\left[ {\begin{array}{*{20}c} {B_{a} D_{b}^{\prime} C_{a} } & {B_{a} C_{b}^{\prime} } \\ {B_{b}^{\prime} C_{a} } & {A_{b}^{\prime} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {v_{i1} } \\ {v_{i2} } \\ \end{array} } \right] $$

(7.19)

which can be written as:

$$ \begin{aligned} \lambda_{i}^{'} = & \omega_{i}^{T} B_{a} D_{b}^{'} C_{a} v_{i} + \omega_{a}^{T} B_{a} C_{b} M\left( {\lambda_{i} } \right)B_{b}^{'} C_{a} v_{i} + \omega_{i}^{T} B_{A} C_{b}^{'} M\left( {\lambda_{i} } \right)B_{b} C_{a} v_{i} \\ & \quad + \omega_{i}^{T} B_{a} C_{b} M\left( {\lambda_{i} } \right)A_{b}^{'} M\left( {\lambda_{i} } \right)B_{b} C_{a} v_{i} \\ \end{aligned} $$

(7.20)

This expression resembles Eq. (7.16) and, in fact, can be factorised to get a more compact relationship. Thus, the eigenvalue sensitivity on a feedback gain, as a function of the original system matrices and the transfer function of the feedback loop, is described by Pagola et al. [6]:

$$ \lambda_{i}^{\prime} = \omega_{i}^{T} B_{a} H\left( {\lambda_{i} } \right)^{\prime} C_{a} v_{i} $$

(7.21)

$$ \left| {\lambda_{i}^{\prime} } \right| = \left| {\omega_{i}^{T} B_{a} } \right| \cdot \left| {H\left( {\lambda_{i} } \right)^{\prime} } \right| \cdot \left| {C_{a} v_{i} } \right| $$

(7.22)

where the term $|\omega_{i}^{T} B_{a} |$ is called the mode controllability of mode i (MC) since relates the effects of the chosen input in the mode displacement. Similarly, the term $|C_{a} v_{i} |$ is called the mode observability of mode i (MO) and relates the effects of the chosen measurement signal of the feedback control in the mode displacement.

Given a common transfer function, for example, the same Energy Storage System (ESS) controlling inter-area oscillations with exactly the same feedback gain, then the relative difference in the magnitude of the mode displacement is given by the MC and MO. The direction of the displacement can be adjusted later by adding phase-lead compensator in the feedback loop considering the necessary compensation angle. In order to compare the effect in the mode displacement of two or more input and two or more measurement signals, the controllability index (CI) and the observability index (OI) are defined [7]. Let $l \in L$ the set of all possible inputs and $\delta \in \Delta$ the set of all possible feedback measurements. Then the controllability index associated with input l (CI _l ) and the observability index associated with signal δ (OI _δ ) are expressed as:

$$ CI_{l} = \frac{{MC_{l} }}{{{}_{l \in L}^{\hbox{max} } MC_{l} }} $$

(7.23)

and

$$ OI_{\delta } = \frac{{MO_{\delta } }}{{{}_{\delta \in \Delta }^{\hbox{max} } MO_{\delta } }} $$

(7.24)

7.3 DPL Scripting and Procedure

All the calculations described in the previous section are programmed in DPL and can be classified into two main parts:

• (a) State-space representation: In order to perform eigenvalue sensitivity, a state-space model of the linearized system is needed. Matrix A gives information of the eigenvalues of interest and the respective left and right eigenvectors as shown in Eqs. (7.3) and (7.4). Matrices B and C are used to calculate the eigenvalue sensitivity Eq. (7.22). In order to allow the users to manipulate some data from the modal analysis calculation, DIgSILENT has included a function to export the system matrix A from the state-space model. This matrix A contains information with concrete physical interpretations (modes), and mathematically speaking, it is uniquely defined. However, matrices B and C of the state-space model are related to the input and output variables; thus, they are unavailable a priori as the user definition/intervention is required. To provide a framework for obtaining the full numerical linear state-space representation in DIgSILENT, this section introduces a procedure to estimate the input and output matrices for any large system with large number of state variables using DPL.

• (b) Eigenvalue sensitivity: CI and OI are calculated according to Eqs. (7.23) and (7.24) for all prospective installation location and feedback signals. The results are exported as vectors in two independent “csv” files for further analysis.

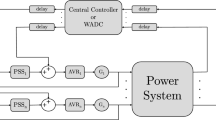
The following programs are coded for the application to the NCIS; however, a guideline to apply them to any system is given. A flow chart of the whole procedure is shown in Fig. 7.1.

Fig. 7.1

Flow chart for eigenvalue sensitivity calculation

The first step is to run the program Main_script_1 which calculates the modal analysis to the open loop system. The modal analysis calculation object (ComMod*) is set to export the output to MATLAB files for system matrices, eigenvalues, left eigenvectors, right eigenvectors and participation factors in a customised path. Figure 7.2 shows the script of Main_script_1.

Fig. 7.2

DPL for modal analysis and output path definition

The execution of Main_script_1 creates seven “mtl” files and two “txt” files in the chosen path. In particular, the file “VariableToIdx_Amat.txt” will be read several times in the code to index the results to their respective state variables.

In order to allow a correct reading of the “VariableToIdx_Amat.txt.” file, the header row must be manually deleted with a text editor such as NotePad++. Any other additional description row in the body of the file must also be deleted, and then the file should contain the same number of rows as the number of state variables. Once this is done, Main_script_2 can be executed. Here, a preparation program reads the state variables and adds them to the All Calculation (ElmRes*) object in the study case. This allows the next programs to perform the necessary calculations over these variables to estimate the matrices B (in Bcalculations) and C (in Ccalculations). After matrices B and C are calculated and stored as IntMat* objects in the study case, the programs Controllability and Observability obtain the mode controllability and mode observability, which are finally used to get and export CI and OI with the program Output. All these five programs are contained inside of the Main_script_2.

Figure 7.3 shows a screenshot of the Main_script_2 element dialog and the contents tab. A general selection (SetSelect*) must be created in the study case and selected in this program. The general selection must contain the prospective installation location buses, which will be used for the calculation of the CI.

Fig. 7.3

DPL Main script_2 screenshot

The DPL script of Main_script_2 is shown in Fig. 7.4. Note that the path specified must be the same as the one used for Main_script_l. This allows the subprograms to read and work with the variables of interest.

Fig. 7.4

DPL for preparation, calculations and exporting results

As mentioned before, the preparation program reads the file “VariableToIdx_Amat.txt” to add the state variables into “All calculation” and to use them in the B and C matrix calculation. This step is necessary for large power systems since the number of states may easily exceed a few hundred and manual setting can be cumbersome. The following subprogram uses the typical structure of the “VariableToIdx_Amat.txt” file to get the state variables. For instance, consider the first three rows of the following “VariableToIdx_Amat.txt” file.

• 1. SING\BESS\PWM BESS ANG.ElmVscmono “phiu”

• 2. SING\BESS\BESS Angamos\Energy.ElmDsl “xE”

• 3. SING\BESS\BESSAngamos\FrequencyControl.ElmDsl “xdpdt”

Here, the first element of each line corresponds to the variable number. Thus, the number in the last line of the file should coincide with the size of the A matrix. Although not used for calculation, this number allows to identify each state variable. The second part of each line is the DIgSILENT path of the element, which is related to the corresponding state variable. This path is used to search the element of interest with a filter (SetFilt*) and assign it to a new IntMon* object in All calculation. Finally, the third part in quotation marks gives always the name of the state, which is used as the selected variable of the IntMon* object. Figure 7.5 shows the subroutine Preparation.

Fig. 7.5

DPL for adding state variables in all calculations

7.3.1 State-Space Representation: Matrix B and C

Contrary to matrix A, matrix B and C are not unique and depend on the user definition. For the following programs, matrix B is calculated assuming that the input variables correspond to active power injections at the buses of the general selection (SetSelect*)—damping regulating devices are considered in this chapter, which modulate active power. Similarly, and for the sake of simplicity, direct observation of all machine speeds is considered as possible feedback signals.

Consider the system subject to a single power variation Δu _i . Thus,

$$ \Delta \dot{x} = A\Delta x + B_{i} \Delta u_{i} $$

(7.25)

Assume this input is a unit step function; thus, Δx(t) = 0, ∀t ≤ 0, and the unit step is suddenly applied at t = 0. Using Forward Euler formula, the following expression is obtained after the first time step (Δt):

$$ \Delta \dot{x}\left( {\Delta t} \right) \approx A\underbrace {\Delta x\left( 0 \right)}_{ = 0} + B_{i} \underbrace {{\Delta u_{i} \left( 0 \right)}}_{ = 1} $$

(7.26)

$$ \Rightarrow B_{i} \approx \Delta \dot{x}\left( {\Delta t} \right) \approx \frac{{\Delta x\left( {\Delta t} \right) - \overbrace {\Delta x\left( 0 \right)}^{ = 0}}}{\Delta t} = \frac{{x\left( {\Delta t} \right) - x\left( 0 \right)}}{\Delta t} $$

(7.27)

Therefore, the column i of the matrix B is estimated by the application of this unit step function; small time steps are required, so the error of the Forward Euler equation is minimal. Based on the superposition principle, all columns of matrix B are determined by repeating this procedure for all buses of the general selection (SetSelect*). Figure 7.6 represents the B matrix calculation flow chart.

Fig. 7.6

Flow chart of matrix B calculation

Figure 7.7 shows a screenshot of the Bcalculation element dialog and content tab. The same general selection (SetSelec*) used in Main_script_2 must be selected. Additionally, a load (ElmLod*) call “Mobile Load” of 100 MW (1 pu) is used for the load step and selected as an external object. The input parameter “s” determines the path of the file “VariableToIdx_Amat.txt” and is assigned to the main program.

Fig. 7.7

“Bcalculation” element dialog and content tab

The script of Bcalculation is shown in Fig. 7.8. The first lines of code prepare the elements and set the simulation times to approximate the coefficients of matrix B after a small time of 0.0001 s. In order to perform the load step, a single switch event (EvtSwitch*) must be manually created. The iteration starts alphabetically creating a node (StaCubic*) and a breaker added to each bus (ElmTerm*) of the general selection. This node then is assigned to the Mobile Load, which is selected for the switch event. Once the load is related to the bus of interest, the initial conditions (ComInc*) and simulation (ComSim*) are executed. An additional program called Creating_1B_column is executed to calculate the coefficients of B with the results from the simulation. The procedure is repeated for all the buses in the general selection. A file called “Input description.out” is generated to allow the user a fast identification of the input definitions.

Fig. 7.8

DPL for calculating matrix B

The script of Creating_1B_column is shown in Fig. 7.9. This subroutine is in charge of the calculation of the coefficients of the ith column of B after the ith load step is applied. The parameter i is entered as an input (called “column”) of the “Creating_1B_column” program, assigned by code in Bcaculation. According to Eq. (7.27), the program needs to read the value of all state variables at t = 0 and at t = Δt (one time step). This is done by reading the “VariableToIdx_Amat.txt” which gives the number of each state, the path of the element related to the state and the name of the state. The index gives the position in B _i related to that state, while the path and name are used to find the element object with a filter. The element together with the variable name allows us to search in the Results element the position of the desired state. Then, the position (named “col” in the script) is used to get the value of the state at both time of interests to calculate the coefficient and assign it to the respective position of matrix B.

Fig. 7.9

DPL for creating a column of matrix B

Consider now the computation of matrix C. Since the output variables are defined as the direct speed observation of all machines, the ith row of this matrix is full of zeros except for one term with value “1” associated with the speed of the ith machine. The program Ccalculation is used to generate this matrix. The input parameter “path” is set in the program Main_cript_2 and allows to read the file “VariableToIdx_Amat.txt” which gives the index of each machine speed variable to save them in matrix Cindex. This matrix is then used to build matrix C. Figure 7.10 shows the script of Ccalculation. Additionally, the file “Output_description.txt” is generated to allow the user an easy access to the output definition.

Fig. 7.10

DPL for getting matrix C

7.3.2 Mode Controllability and Observability

Mode controllability is calculated using the matrix B and the left eigenvector related to the eigenvalue of interest. To obtain this eigenvector, the index of the respective eigenvalue is needed. This is obtained by reading the “Evals.mtl” file generated from Main_script_1 and by filtering the modes using the previous information from a Modal Analysis calculation. In this code, only the imaginary part is used to select the eigenvalue, but a more restrictive searching (in the case of several modes in the same frequency range) could be achieved by adding a filter to the real part as well. After getting the mode index, the program proceeds to read the file “lEV.mtl” saving in two matrices the real and imaginary parts of the left eigenvector of interest. These values are used to get the magnitude of the mode controllability indices for each location, which are saved in the matrix Mctr.IntMat. Figure 7.11 shows the subroutine Controllability.

Fig. 7.11

DPL for obtaining mode controllability

For the mode observability, the calculation is similar by using the matrix C and the right eigenvector. Since the rows of C contain only one nonzero element, the matrix multiplication gives one element of the right eigenvector (in the position of the nonzero element) for each output. Then, the calculation is simplified using the matrix Cindex. Figure 7.12 shows the subroutine Observability.

Fig. 7.12

DPL for obtaining mode observability

The final step consists on normalising the mode controllability and observability on their higher values to obtain CI and OI. The indices are written in two separate output csv file. Figure 7.13 shows the subroutine Output which performs the described task.

Fig. 7.13

DPL for writing the output files

7.3.3 Guideline to Execute the Program for Any Arbitrary System

• Choose your working path and assign it to the variable path in the program Main_script_1 and Main_script_2.

• Perform modal analysis calculation to determine the mode of interest. If needed, modify the search range for the imaginary part of the eigenvalue of interest to the most suitable range for your system. This change is done in the programs Controllability and Observability.

• Create a constant power load of 100 MW (base power in DIgSILENT by default) and select it as an external object in program Bcalculation.

• Create a switch event in the active study case.

• Create a general selection in the active study case with the prospective installation locations and select it in program Main_script_2 and Bcalculation.

• Replace the string “SING” by the name of your grid (ElmNet)—Typically “Grid”—in programs Preparation, Bcalculation and Ccalculation.

• Execute Main_script_1 and manually delete header line and any other description line without index, path and variable within the body of the file VariableToIdx_Amat.txt. For verification purposes, remember that the number of lines in the file should be the same as the number of state variables.

• Execute Main_script_2.

7.4 Real System Application: The Northern Chile Interconnected System

The Northern Chile Interconnected System is a very particular system that, as to 2015, had an installed capacity of 4150 MW, maximum demand around 2400 MW and an inertia of about 3.86 s base on the installed power. The NCIS has been connected to the Argentinian Interconnected System (AIS) since 2015, improving its operational performance in aspects such as frequency quality and voltage profiles. However, without proper control actions, the appearance of a critical inter-area oscillation between both systems is imminent. Hence, the use of damping regulating devices, such as ESS, through active power injection is attractive to solve this problem [7, 8]. In order to decide the ESS installation location, thirty-one bus candidates in the NCIS are selected and evaluated using CI. Similarly, assuming ideal wide-area measurements, twenty feedback signals (machine speed) are proposed and analysed with OI.

In a conventional project analysis, the pair location/signal with higher CI and OI is tested by performing modal analysis and time-domain simulations when the damping regulating device is connected. For the sake of clarity, this analysis is separated to see the independent effects of each decision. Both location and signal are compared for the worst, the best and one intermedium candidate.

Although any ESS can be employed, e.g. flywheels, ultracapacitors, others, for simplicity, the Battery Energy Storage (BES) model from the DIgSILENT library is used. The template used is “BatteryWithFrequencyControl_10kV_30MVA” for which the nominal power has been changed to 50 MW; the dead band is neglected and the droop gain of the frequency control is set to 0.002. Additionally, a phase compensator is included to the frequency control loop to add the necessary angle compensation for the inter-area mode.

7.4.1 Controllability Analysis

The results of the controllability index for the thirty-one prospective locations obtained from the file CI.csv are plotted in the NCIS map and shown in Fig. 7.14. This map shows a pattern where the CI increases in the north direction as the buses get away from the interconnection with the AIS.

Fig. 7.14

CI results in the NCIS

In order to compare the effect of the installation location alone, three different BES locations for a common feedback signal (CTTAR) are analysed. The CI and results from Modal analysis are shown in Table 7.1. The base case is defined as the case without BES.

Table 7.1 Installation location comparison

The improvement of the damping ratio, which gives a measurement of the mode displacement, is consistent with the CI. In addition, a time-domain simulation after a 10 ms three-phase short-circuit in bus Crucero is performed to compare the effects of bus location Andes and Parinacota. Again, the results show satisfactory correlation (Fig. 7.15).

Fig. 7.15

Machine speeds for different BES locations

7.4.2 Observability Analysis

The results of the observability index are shown in Table 7.2. The results show that the machine speeds in the NCIS have in general good observability, while the speed of the equivalent machine in the AIS is not a good option as a feedback signal.

Table 7.2 Observability index for NCIS-AIS

A detailed comparison of three feedback signals, and the parameters of the phase compensator when the BES is connected in bus Andes, is shown in Table 7.3. The base case is defined as the case without BES.

Table 7.3 Feedback signal comparison

Once again, the damping ratio improvement, as a measurement of the mode displacement, is consistent with the magnitude of the OI. A time-domain simulation after a 10 ms three-phase short-circuit in bus Crucero is performed to compare the effects of the feedback signals CTTAR and PAM when the BES is connected in bus Andes. The dynamic simulation is shown in Fig. 7.16. The results show agreement with the eigenvalue sensitivity approach.

Fig. 7.16

Machine speeds for different feedback signals

7.4.3 Final Remarks

The proposed algorithms in this chapter proved to be effective to give a comparison index when a large number of installation locations and feedback signals are considered in a real system. Thus, the effects of the damping regulating devices considering the best location/signal candidates—a small subset of the original analysis set—are evaluated with modal analysis and time-domain simulations for final selection. Note that, despite using the worse installation location in Table 7.2, the damping ratio can still be improved by selecting the appropriate feedback signal. For a more realistic analysis, this work can be improved by adding communication delays and frequency measurement units that can obtain frequency at any bus. Still, the scripts and applications presented in this document set the basis for additional development, including similar approaches that make use of state-space representation for real large-scale systems.

7.5 Conclusions

An approach to determine wide-area signals and installation locations of damping regulating devices using eigenvalue sensitivity has been explained and programmed in DPL. A state-space representation is estimated from dynamic simulations and used in addition to controllability and observability indices to reduce the number of location/signal. The effects of choosing the reduced set of location/signal candidates, when a damping regulating device is connected, are assessed with modal analysis and time-domain simulations. The approach is applied to analyse the critical inter-area oscillations between NCIS and AIS, and the independent effects of location and signal are studied for the connection of a BES in the NCIS. The indices are proven to be effective indicating the location/signal which drives the system from an almost unstable operation to conditions with a damping ratio greater than 11%. All programs provided in this chapter are generic and set the basis for further development in control and analysis of power systems using state-space representation.