Abstract
Interpolation is a fundamental logical property with applications in mathematics, computer science, and artificial intelligence. In this paper, we develop a general method of translating a semantic description of modal logics via Kripke models into a constructive proof of the Lyndon interpolation property (LIP) via labelled sequents. Using this method we demonstrate that all frame conditions representable as Horn formulas imply the LIP and that all 15 logics of the modal cube, as well as the infinite family of transitive Geach logics, enjoy the LIP.
This material is based upon work supported by the Austrian Science Fund (FWF) Lise Meitner Grant M 1770-N25.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Unlike internal formalisms, external ones cannot generally be translated into formulas, typically because of the essential use of semantic elements, e.g., Kripke worlds.
- 2.
The method also works for sequence- and set-based sequents.
- 3.
NNF is used here to simplify the notation rather than out of necessity and means that negation is restricted to propositional atoms, creating two literals P and \(\overline{P}\) for each atom. Primary connectives are \(\wedge \), \(\vee \), \(\Box \), and \(\Diamond \). Negation \(\overline{A}\) is a function of a formula A defined via De Morgan laws. \(A \rightarrow B := \overline{A}\vee B\).
- 4.
It also holds for \(l_i=0\): the empty conjunction is \(\top \) and \(\mathcal {M}, \left[ \!\left[ \mathsf {w}\right] \!\right] \Vdash \Diamond \top \).
- 5.
For each eigenvariable \(\mathsf {y}_j\) we have collected all formulas labelled with \(\mathsf {y}_j\) within each disjunct into one labelled formula by transforming
 into
into 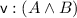 if more than one formula has this label or by adding
if more than one formula has this label or by adding 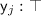 if no formula has.
if no formula has.
References
Amir, E., McIlraith, S.: Partition-based logical reasoning for first-order and propositional theories. Artif. Intell. 162(1–2), 49–88 (2005)
Bílková, M.: A note on uniform interpolation proofs in modal deep inference calculi. In: Bezhanishvili, N., Löbner, S., Schwabe, K., Spada, L. (eds.) TbiLLC 2009. LNCS (LNAI), vol. 6618, pp. 30–45. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22303-7_3
Brotherston, J., Goré, R.: Craig interpolation in displayable logics. In: Brünnler, K., Metcalfe, G. (eds.) TABLEAUX 2011. LNCS (LNAI), vol. 6793, pp. 88–103. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22119-4_9
ten Cate, B., Franconi, E., Seylan, İ.: Beth definability in expressive description logics. J. Arti. Intell. Res. 48(1), 347–414 (2013)
Dyckhoff, R., Negri, S.: Geometrisation of first-order logic. Bull. Symbolic Logic 21(2), 123–163 (2015)
Fitting, M., Kuznets, R.: Modal interpolation via nested sequents. Ann. Pure Appl. Logic 166(3), 274–305 (2015)
Garson, J.: Modal logic. In: Zalta, E.N., (ed.) The Stanford Encyclopedia of Philosophy (2016). http://plato.stanford.edu/entries/logic-modal/
Goré, R., Ramanayake, R.: Labelled tree sequents, tree hypersequents and nested (deep) sequents. In: Bolander, T., Braüner, T., Ghilardi, S., Moss, L. (eds.) Advances in Modal Logic, vol. 9, pp. 279–299. College Publications (2012)
Herzig, A., Mengin, J.: Uniform interpolation by resolution in modal logic. In: Hölldobler, S., Lutz, C., Wansing, H. (eds.) JELIA 2008. LNCS (LNAI), vol. 5293, pp. 219–231. Springer, Heidelberg (2008). doi:10.1007/978-3-540-87803-2_19
Iemhoff, R.: Uniform interpolation and sequent calculi in modal logic. Preprint 325, Logic Group Preprint Series (2015)
Kripke, S.A.: Semantical analysis of modal logic I: normal modal propositional calculi. Z. Math. Logik Grundlagen Math. 9(5–6), 67–96 (1963)
Kuznets, R.: Craig interpolation via hypersequents. In: Probst, D., Schuster, P. (eds.) Concepts of Proof in Mathematics, Philosophy, and Computer Science. Ontos Mathematical Logic, vol. 6, pp. 193–214. De Gruyter, Berlin (2016)
Kuznets, R.: Interpolation method for multicomponent sequent calculi. In: Artemov, S., Nerode, A. (eds.) LFCS 2016. LNCS, vol. 9537, pp. 202–218. Springer, Heidelberg (2016). doi:10.1007/978-3-319-27683-0_15
Maksimova, L.L.: Absence of the interpolation property in the consistent normal modal extensions of the Dummett logic. Algebra Logic 21(6), 460–463 (1982)
Marx, M., Venema, Y.: Multi-dimensional Modal Logic. Applied Logic Series, vol. 4. Springer, Heidelberg (1997)
Negri, S., von Plato, J.: Proof Analysis: A Contribution to Hilbert’s Last Problem. Cambridge University Press, Cambridge (2011)
Pattinson, D.: The logic of exact covers: completeness and uniform interpolation. In: 2013 28th Annual ACM/IEEE Symposium on Logic in Computer Science, pp. 418–427. IEEE (2013)
Thomason, R.: Logic and artificial intelligence. In: Zalta, E.N. (ed.) The Stanford Encyclopedia of Philosophy (2014). http://plato.stanford.edu/entries/logic-ai/
Acknowledgments
I am grateful to M. Fitting, whose idea started this interpolation project. I thank S. Negri for encouragement, V. Sikimić for procuring a source not available online, Y. Venema and M. Marx for valuable information on the non-constructive method. I am deeply indebted to B. Lellmann, who is always ready to listen and has provided many inspiring suggestions for improving this paper. I thank the anonymous reviewers for the suggestions on terminology.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing AG
About this paper
Cite this paper
Kuznets, R. (2016). Proving Craig and Lyndon Interpolation Using Labelled Sequent Calculi. In: Michael, L., Kakas, A. (eds) Logics in Artificial Intelligence. JELIA 2016. Lecture Notes in Computer Science(), vol 10021. Springer, Cham. https://doi.org/10.1007/978-3-319-48758-8_21
Download citation
DOI: https://doi.org/10.1007/978-3-319-48758-8_21
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-48757-1
Online ISBN: 978-3-319-48758-8
eBook Packages: Computer ScienceComputer Science (R0)


 into
into 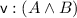 if more than one formula has this label or by adding
if more than one formula has this label or by adding 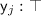 if no formula has.
if no formula has.