Abstract
Programs with floating-point computations are often derived from mathematical models or designed with the semantics of the real numbers in mind. However, for a given input, the computed path with floating-point numbers may significantly differ from the path corresponding to the same computation with real numbers. As a consequence, developers do not know whether the program can actually produce very unexpected outputs. We introduce here a new constraint-based approach that searches for test cases in the part of the over-approximation where errors due to floating-point arithmetic could lead to unexpected decisions.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
In numerous applications, programs with floating-point computations are derived from mathematical models over the real numbers. However, computations on floating-point numbers are different from calculations in an idealised semanticsFootnote 1 of real numbers [8]. For some values of the input variables, the result of a sequence of operations over the floating-point numbers can be significantly different from the result of the corresponding mathematical operations over the real numbers. As a consequence, the computed path with floating-point numbers may differ from the path corresponding to the same computation with real numbers. This can entail wrong outputs and dangerous decisions of critical systems. That’s why identifying these values is a crucial issue for programs controlling critical systems.
Abstract interpretation based error analysis [3] of finite precision implementations computes an over-approximation of the errors due to floating-point operations. The point is that state-of-the-art tools [6] may generate numerous false alarms. In [16], we introduced a hybrid approach combining abstract interpretation and constraint programming techniques that reduces the number of false alarms. However, the remaining false alarms are very embarrassing since we cannot know whether the predicted unstable behaviors will occur with actual data.
More formally, consider a program P, a set of intervals I defining the expected input values of P, and an output variable x of P on which depend critical decisions, e.g., activating an anti-lock braking system. Let \([\underline{x}_{\scriptscriptstyle \mathbb {R}} , \overline{x}_{\scriptscriptstyle \mathbb {R}}]\) be a sharp approximation over the set of real numbers \(\mathbb {R}\) of the domain of variable x for any input of P. \([\underline{x}_{\scriptscriptstyle \mathbb {F}} , \overline{x}_{\scriptscriptstyle \mathbb {F}}]\) stands for the domain of variable x in the over-approximation computed over the set of floating-point \(\mathbb {F}\) for input values of I. The range \([\underline{x}_{\scriptscriptstyle \mathbb {R}} , \overline{x}_{\scriptscriptstyle \mathbb {R}}]\) can be determined by calculation or from physical limits. It includes a small tolerance to take into account approximation errors, e.g. measurement, statistical, or even floating-point arithmetic errors. This tolerance – specified by the user – defines an acceptable loss of accuracy between the value computed over the floating-point numbers and the value calculated over the real numbers. Values outside the interval \([\underline{x}_{\scriptscriptstyle \mathbb {R}} , \overline{x}_{\scriptscriptstyle \mathbb {R}}]\) can lead a program to misbehave, e.g. take a wrong branch in the control flow.
The problem we address in this paper consists of verifying whether there exist critical values in I for which the program can actually produce a result value of x inside the suspicious intervals \([\underline{x}_{\scriptscriptstyle \mathbb {F}} , \underline{x}_{\scriptscriptstyle \mathbb {R}})\) and \((\overline{x}_{\scriptscriptstyle \mathbb {R}} , \overline{x}_{\scriptscriptstyle \mathbb {F}}]\). To handle this problem, we introduce a new constraint-based approach that searches for test cases that hit the suspicious intervals in programs with floating-point computations. In other words, our framework reduces this test case generation problem to a constraint-solving problem over the floating-point numbers where the domain of a critical decision variable has been shrunk to a suspicious interval. A constraint solver – based on filtering techniques designed to handle constraints over floating-point numbers – is used to search values for the input data. Preliminary results of experiments on small programs with classical floating-point errors are encouraging.
The CPBPV_FP, the system we developed, outperforms generate and test methods for programs with more than one input variable. Moreover, these search strategies can prove in many cases that no critical value exists.
2 Motivating Example
Before going into the details, we illustrate our approach on a small example. Assume we want to compute the area of a triangle from the lengths of its sides a, b, and c with Heron’s formula:
where \(s = (a+b+c)/2.\) The C program in Fig. 1 implements this formula, when a is the longest side of the triangle.
The test of line 5 ensures that the given lengths form a valid triangle.
Now, suppose that the input domains are  and
and  . Over the real numbers,
. Over the real numbers,  is greater than any of the sides of the triangle and
is greater than any of the sides of the triangle and  cannot be negative. Moreover,
cannot be negative. Moreover,  cannot be greater than 156.25 over the real numbers since the triangle area is maximized for a right triangle with \(b=c=5\) and \(a=5\sqrt{2}\). However, these properties may not hold over the floating-point numbers because absorption and cancellation phenomena can occurFootnote 2.
cannot be greater than 156.25 over the real numbers since the triangle area is maximized for a right triangle with \(b=c=5\) and \(a=5\sqrt{2}\). However, these properties may not hold over the floating-point numbers because absorption and cancellation phenomena can occurFootnote 2.
Tools performing value analysis over the floating-point numbers [6, 15] approximate the domain of  to the interval \([-1262.21 , 979.01]\). Since this domain is an over-approximation, we do not know whether input values leading to
to the interval \([-1262.21 , 979.01]\). Since this domain is an over-approximation, we do not know whether input values leading to  \(<0\) or
\(<0\) or  \(>156.25\) actually exist. Note that input domains –here a \(\in \) [5,10] and b, c \(\in \) [0,5]– are usually provided by the user.
\(>156.25\) actually exist. Note that input domains –here a \(\in \) [5,10] and b, c \(\in \) [0,5]– are usually provided by the user.
Assume the value of the toleranceFootnote 3 \(\varepsilon \) is \( 10^{-5}\), the suspicious intervals for  are \([-1262.21 , -10^{-5})\) and \((156.25001 , 979.01]\). CPBPV_FP, the system we developed, generated test cases for both intervals:
are \([-1262.21 , -10^{-5})\) and \((156.25001 , 979.01]\). CPBPV_FP, the system we developed, generated test cases for both intervals:
-
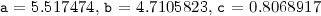 , and
, and  ;
; -
 ,
,  , and
, and  equals 156.25003.
equals 156.25003.
CPBPV_FP could also prove the absence of test cases for a tolerance \(\varepsilon = 10^{-3}\) with  .
.
In order to limit the loss of accuracy due to cancellation [8], line 7 of Heron’s program can be rewritten as follows:

However, there are still some problems with this optimized program. Indeed, CPBPV_FP found the test case  ,
,  ,
,  , and
, and  equals \(-1.0000001 \cdot 10^{-5}\) for interval \( [-1262.21 , -10^{-5})\) of
equals \(-1.0000001 \cdot 10^{-5}\) for interval \( [-1262.21 , -10^{-5})\) of  . There are no more problems in the interval \( (156.25001 , 979.01]\) and CPBPV_FP did prove it.
. There are no more problems in the interval \( (156.25001 , 979.01]\) and CPBPV_FP did prove it.
3 Framework for Generating Test Cases
This section details the framework we designed to generate test cases reaching suspicious intervals for a variable x in a program P with floating-point computations.
The kernel of our framework is FPCS [1, 12–14], a solver for constraints over the floating-point numbers; that’s to say a symbolic execution approach for floating-point problems which combines interval propagation with explicit search for satisfiable floating-point assignments. FPCS is used inside the CPBPV bounded model checking framework [5]. CPBPV_FP is the adaptation of CPBPV for generating test cases that hit the suspicious intervals in programs with floating-point computations.
The inputs of CPBPV_FP are: P, an annotated program; a critical test ct for variable x; \([\underline{x}_{\scriptscriptstyle \mathbb {F}} , \underline{x}_{\scriptscriptstyle \mathbb {R}})\) or \((\overline{x}_{\scriptscriptstyle \mathbb {R}} , \overline{x}_{\scriptscriptstyle \mathbb {F}}]\), a suspicious interval for x. Annotations of P specify the range of the input variables of P as well as the suspicious interval for x. The latter assertion is just posted before the critical test ct.
To compute the suspicious interval for x, we approximate the domain of x over the real numbers by \([\underline{x}_{\scriptscriptstyle \mathbb {R}} , \overline{x}_{\scriptscriptstyle \mathbb {R}}]\), and over the floating-point numbers by \([\underline{x}_{\scriptscriptstyle \mathbb {F}} , \overline{x}_{\scriptscriptstyle \mathbb {F}}]\). These approximations are computed with rAiCp [16], a hybrid system that combines abstract interpretation and constraint programming techniques in a single static and automatic analysis. The current implementation of rAiCp is based upon the abstract interpreter Fluctuat [6], the constraint solver over the reals RealPaver [10] and FPCS. The suspicious intervals for variable x are denoted \([\underline{x}_{\scriptscriptstyle \mathbb {F}} , \underline{x}_{\scriptscriptstyle \mathbb {R}})\) and \((\overline{x}_{\scriptscriptstyle \mathbb {R}} , \overline{x}_{\scriptscriptstyle \mathbb {F}}]\).
CPBPV_FP performs first some pre-processing: P is transformed into DSA-like formFootnote 4. If the program contains loops, CPBPV_FP unfolds loops k times where k is a user specified constant. Loops are handled in CPBPV and rAiCp with standard unfolding and abstraction techniquesFootnote 5. So, there are no more loops in the program when we start the constraint generation process. Standard slicing operations are also performed to reduce the size of the control flow graph.
In a second step, CPBPV_FP searches for executable paths reaching ct. For each of these paths, the collected constraints are sent to FPCS, which solves the corresponding constraint systems over the floating point numbers. FPCS returns either a satisfiable instantiation of the input variables of P, or \(\emptyset \).
As said before, FPCS [1, 12–14] is a constraint solver designed to solve a set of constraints over floating-point numbers without losing any solution. It uses 2B-consistency along with projection functions adapted to floating-point arithmetic [1, 13] to filter constraints over the floating-point numbers. FPCS also provides stronger consistencies like kB-consistencies, which allow better filtering results.
The search of solutions in constraint systems over floating numbers is trickier than the standard bisection-based search in constraint systems over intervals of real numbers. Thus, we have also implemented different strategies combining selection of specific points and pruning. Details on theses strategies are given in the experiments section.
CPBPV_FP ends up with one of the following results:
-
a test case proving that P can produce a suspicious value for x;
-
a proof that no test case reaching the suspicious interval can be generated: this is the case if the loops in P cannot be unfolded beyond the bound k (See [5] for details on bounded unfolding) ;
-
an inconclusive answer: no test case could be generated but the loops in P could be unfolded beyond the bound k. In other words, the process is incomplete and we cannot conclude whether P may produce a suspicious value.
4 Preliminary Experiments
We experimented with CPBPV_FP on six small programs with cancellation and absorption phenomena, two very common pitfalls of floating-point arithmetic. The benchmarks are listed in the first two columns of Table 1.
First two benchmarks concern the heron program and the optimized_heron program with the suspicious intervals described in the Sect. 1.
Program slope (see Fig. 2) approximates the derivative of the square function \(f(x) = x^2\) at a given point \(x_0\). More precisely, it computes the slope of a nearby secant line with a finite difference quotient: \(f'(x_0) \approx \frac{f(x_0 + h) - f(x_0 - h)}{2h}\). Over the real numbers, the smaller h is, the more accurate the formula is. For this function, the derivative is given by \(f'(x) = 2x\) which yields exactly 26 for \(x = 13\). Over the floats, Fluctuat [6] approximates the return value of the slope program to the interval \([0 , 25943]\) when \(h \in [10^{-6} , 10^{-3}]\) and \(x_0=13\).
Program polynomial in Fig. 3 illustrates an absorption phenomenon. It computes the polynomial \((a^2+b+10^{-5})*c\). For input domains \(a \in [10^3 , 10^4]\), \(b \in [0 , 1]\) and \(c \in [10^3 , 10^4]\), the minimum value of the polynomial over the real numbers is equal to 1000000000.01.
simple_interpolator and simple square are two benches extracted from [9]. The first bench computes an interpolator, affine by sub-intervals while the second is a rewrite of a square root function used in an industrial context.
All experiments were done on an Intel Core 2 Duo at 2.8 GHz with 4 GB of memory running 64-bit Linux. We assume C programs handling IEEE 754 compliant floating-point arithmetic, intended to be compiled with GCC without any optimization option and run on a x86_64 architecture managed by a 64-bit Linux operating system. Rounding mode was to the nearest, i.e., where ties round to the nearest even digit in the required position.
4.1 Strategies and Solvers
We run CPBPV_FP with the following search strategies for the FPCS solver:
-
 : standard prune&bisection-based search used in constraint-systems over intervals: splits the selected variable domain in two domains of equal size;
: standard prune&bisection-based search used in constraint-systems over intervals: splits the selected variable domain in two domains of equal size; -
 : splits the domain of the selected variable in five intervals:
: splits the domain of the selected variable in five intervals:-
Three degenerated intervals containing only a single floating point number: the smallest float l, the largest float r, and the mid-point m;
-
Two open intervals \((l , m)\) and \((m , r)\);
-
-
 : selects 3 degenerated intervals containing only a single floating point number: the smallest float l, the largest float r, and the mid-point m. Hence,
: selects 3 degenerated intervals containing only a single floating point number: the smallest float l, the largest float r, and the mid-point m. Hence,  is an incomplete method that might miss some solutions.
is an incomplete method that might miss some solutions.
For all these strategies, we select first the variables with the largest domain and we perform a 3B−consistency filtering step before starting the splitting process.
We compared CPBPV_FP with CBMC [4] and CDFL [7], two state-of-the-art software bounded model checkers based on SAT solvers that are able to deal with floating-point computations. We also run a simple generate & test strategy: the program is run with randomly generated input values and we test whether the result is inside the suspicious interval. The process is stopped as soon as a test case hitting the suspicious interval is found.
4.2 Results
Table 1 reports the results for the other strategies and solvers. Since strategy  is incomplete, we indicate whether a test case was found or not. Column
is incomplete, we indicate whether a test case was found or not. Column  specifies whether a test case actually exists. Note that the computation times of CBMC and CDFL include the pre-processing time for generating the constraint systems; the pre-processing time required by CPBPV is around 0.6 s but CPBPV is a non-optimised system written in
specifies whether a test case actually exists. Note that the computation times of CBMC and CDFL include the pre-processing time for generating the constraint systems; the pre-processing time required by CPBPV is around 0.6 s but CPBPV is a non-optimised system written in  .
.
5 Discussion
5.1 Results Analysis
The generate & test strategy behaves quite well on programs with only one input variable when a test case exists but it is unable to find any test case for programs with more than one input variable. More precisely, it found a test case in less than 0.008 s for the 6 suspicious intervals of program  and for program
and for program  . The generate & test strategy failed to find a test within 180 s in all other cases. Of course, this strategy cannot show that there is no test case reaching the suspicious interval; so, it is of little interest here.
. The generate & test strategy failed to find a test within 180 s in all other cases. Of course, this strategy cannot show that there is no test case reaching the suspicious interval; so, it is of little interest here.
Strategy  is definitely the most efficient and most robust one on all these benchmarks. Note that CBMC and CDFL could neither handle the initial, nor the optimized version of program
is definitely the most efficient and most robust one on all these benchmarks. Note that CBMC and CDFL could neither handle the initial, nor the optimized version of program  in a timeout of 20 min whereas FPCS found solutions in a reasonable time.
in a timeout of 20 min whereas FPCS found solutions in a reasonable time.
These preliminary results are very encouraging: they show that CPBPV_FP is effective for generating test cases for suspicious values outside the range of acceptable values on small programs with classical floating-point errors. More importantly, a strong point of CPBPV_FP is definitely its refutation capabilities.
Of course, experiments on more significant benchmarks and on real applications are still necessary to evaluate the full capabilities and limits of CPBPV_FP.
5.2 Related and Further Work
The goals of software bounded model checkers based on SAT solvers are close to our approach. The point is that SAT solvers tend to be inefficient on these problems due to the size of the domains of floating-point variables and the cost of bit-vector operations [7]. CDFL [7] tries to address this issue by embedding an abstract domain in the conflict driven clause learning algorithm of a SAT solver. SAT solvers often use bitwise representations of numerical operations, which may be very expensive (e.g., thousands of variables for one equation in CDFL). Brain et al. [2, 11] have recently introduced a bit-precise decision procedure for the theory of floating-point arithmetic. The core of their approach is a generalization of the conflict-driven clause-learning algorithm used in modern SAT solvers. Their technique is significantly faster than a bit-vector encoding approach. Note that the constraint programming techniques used in our approach are better suited to generate several test cases than these SAT-based approaches. The advantage of CP is that it provides a uniform framework for representing and handling integers, real numbers and floats. A new abstract-interpretation based robustness analysis of finite precision implementations has recently been proposed [9] for sound rounding error propagation in a given path in presence of unstable tests.
A close connection between our floating-point solvers and the two above-mentioned approaches is certainly worth exploring.
A second direction for further work concerns the integration of our constraint-based approach with new abstract-interpretation based robustness analysis of finite precision implementations for sound rounding error propagation in a given path in presence of unstable tests.
Notes
- 1.
That’s to say, computations as close as possible to the mathematical semantics of the real numbers; for instance, computations with arbitrary precision or computer algebra systems.
- 2.
Let’s remind that absorption in an addition occurs when adding two numbers of very different order of magnitude, and the result is the value of the biggest number, i.e., when \(x+y\) with \(y\ne 0\) yields x. Cancellation occurs in \(s-a\) when s is so close to a that the subtraction cancels most of the significant digits of s and a.
- 3.
Note that even this small tolerance may lead to an exception in statement 9.
- 4.
DSA stands for Dynamic Single Assignment. In DSA-like form, all variables are assigned exactly once in each execution path.
- 5.
In bounded model checking, k is usually increased until a counter-example is found or until the number of time units is large enough for the application.
References
Botella, B., Gotlieb, A., Michel, C.: Symbolic execution of floating-point computations. Softw. Test. Verif. Reliab. 16(2), 97–121 (2006)
Brain, M., D’Silva, V., Griggio, A., Haller, L., Kroening, D.: Interpolation-based verification of floating-point programs with abstract CDCL. In: Fähndrich, M., Logozzo, F. (eds.) Static Analysis. LNCS, vol. 7935, pp. 412–432. Springer, Heidelberg (2013)
Chen, L., Miné, A., Cousot, P.: A sound floating-point polyhedra abstract domain. In: Ramalingam, G. (ed.) APLAS 2008. LNCS, vol. 5356, pp. 3–18. Springer, Heidelberg (2008)
Clarke, E., Kroning, D., Lerda, F.: A tool for checking ANSI-C programs. In: Jensen, K., Podelski, A. (eds.) TACAS 2004. LNCS, vol. 2988, pp. 168–176. Springer, Heidelberg (2004)
Collavizza, H., Rueher, M., Van Hentenryck, P.: A constraint-programming framework for bounded program verification. Constr. J. 15(2), 238–264 (2010)
Delmas, D., Goubault, E., Putot, S., Souyris, J., Tekkal, K., Védrine, F.: Towards an industrial use of FLUCTUAT on safety-critical avionics software. In: Alpuente, M., Cook, B., Joubert, C. (eds.) FMICS 2009. LNCS, vol. 5825, pp. 53–69. Springer, Heidelberg (2009)
D’Silva, V., Haller, L., Kroening, D., Tautschnig, M.: Numeric bounds analysis with conflict-driven learning. In: Flanagan, C., König, B. (eds.) TACAS 2012. LNCS, vol. 7214, pp. 48–63. Springer, Heidelberg (2012)
Goldberg, D.: What every computer scientist should know about floating point arithmetic. ACM Comput. Surv. 23(1), 5–48 (1991)
Goubault, E., Putot, S.: Robustness analysis of finite precision implementations. In: Shan, C. (ed.) APLAS 2013. LNCS, vol. 8301, pp. 50–57. Springer, Heidelberg (2013)
Granvilliers, L., Benhamou, F.: Algorithm 852: RealPaver: an interval solver using constraint satisfaction techniques. ACM Trans. Math. Softw. 32(1), 138–156 (2006)
Haller, L., Griggio, A., Brain, M., Kroening, D.: Deciding floating-point logic with systematic abstraction. In: Formal Methods in Computer-Aided Design, FMCAD, pp. 131–140. IEEE (2012)
Marre, B., Michel, C.: Improving the floating point addition and subtraction constraints. In: Cohen, D. (ed.) CP 2010. LNCS, vol. 6308, pp. 360–367. Springer, Heidelberg (2010)
Michel, C.: Exact projection functions for floating-point number constraints. In: 7th International Symposium on Artificial Intelligence and Mathematics (2002)
Michel, C., Rueher, M., Lebbah, Y.: Solving constraints over floating-point numbers. In: Walsh, T. (ed.) CP 2001. LNCS, vol. 2239, pp. 524–538. Springer, Heidelberg (2001)
Ponsini, O., Michel, C., Rueher, M.: Refining abstract interpretation based value analysis with constraint programming techniques. In: Milano, M. (ed.) CP 2012. LNCS, vol. 7514, pp. 593–607. Springer, Heidelberg (2012)
Ponsini, O., Michel, C., Rueher, M.: Verifying floating-point programs with constraint programming and abstract interpretation techniques. Autom. Softw. Eng. 23(2), 191–217 (2016)
Acknowledgments
This work was partially supported by ANR COVERIF (ANR-15-CE25-0002).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 IFIP International Federation for Information Processing
About this paper
Cite this paper
Collavizza, H., Michel, C., Rueher, M. (2016). Searching Critical Values for Floating-Point Programs. In: Wotawa, F., Nica, M., Kushik, N. (eds) Testing Software and Systems. ICTSS 2016. Lecture Notes in Computer Science(), vol 9976. Springer, Cham. https://doi.org/10.1007/978-3-319-47443-4_13
Download citation
DOI: https://doi.org/10.1007/978-3-319-47443-4_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-47442-7
Online ISBN: 978-3-319-47443-4
eBook Packages: Computer ScienceComputer Science (R0)






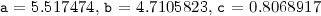 , and
, and  ;
; ,
,  , and
, and  equals 156.25003.
equals 156.25003.

 : standard prune&bisection-based search used in constraint-systems over intervals: splits the selected variable domain in two domains of equal size;
: standard prune&bisection-based search used in constraint-systems over intervals: splits the selected variable domain in two domains of equal size; : splits the domain of the selected variable in five intervals:
: splits the domain of the selected variable in five intervals: : selects 3 degenerated intervals containing only a single floating point number: the smallest float l, the largest float r, and the mid-point m. Hence,
: selects 3 degenerated intervals containing only a single floating point number: the smallest float l, the largest float r, and the mid-point m. Hence,  is an incomplete method that might miss some solutions.
is an incomplete method that might miss some solutions.