1 Introduction

Three-D personalised cardiac models simulate the physical behaviour of a patient heart, in order to perform advanced analysis of the cardiac function. The movement of the myocardium is calculated under the influence of simulated electromechanics and haemodynamic condition, which requires complex and expensive calculations, particularly as the spatial and temporal resolution of the model increases (1 h per heart beat, even several days for some models).

This computational burden particularly impacts applications of the models where many simulations are required. The model personalisation phase (fitting the available clinical data) is particularly impacted, slowing the study of clinical applications such as disease caracterisation and prediction of case evolution

To tackle this computational burden, surrogate models of the cardiac function have been developed, for example for uncertainty quantification [1] or probability estimation [2] over the cardiac parameters. Those models usually rely on regression models which require many pre-computations to approximate nonlinear behaviours, thus scaling badly as the number of varying parameters increases.

Here we built a multiscale cardiac model by developping an novel coupling method between an original 3D cardiac model and a reduced lumped “0D” version of the same model. While the coupling of different scales has been used to improve boundary conditions in cardiac modelling and computational fluid dynamics [3], we propose here the simultaneous simulation of the same model at different scales, which enables extremely fast approximations of the behaviour of the 3D model with 0D simulations. It provides a natural approximation of all the desired cardiac values. Furthermore, we demonstrate the efficiency of the multiscale 0D/3D model when plugged into a personalisation process driven by the genetic algorithm CMA-ES. This creates a very fast and computationally efficient personalisation agent, successfully tested on the personalisation of 34 hearts with different geometries (Fig. 1).

Fig. 1.
figure 1

Multiscale model and personalisation pipeline

Full size image

2 Multiscale Cardiac Model

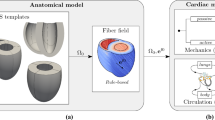
In order to build a computer model of the myocardium, one needs different components to represent the passive stiffness, the active contraction and the boundary conditions (hemodynamics). We use here the Bestel-Clement-Sorine model (BCS) of the sarcomere contraction, in conjonction with the Mooney-Rivlin model for passive elasticity as described in [4]. Hemodynamics are represented through global values of pressures and flows in the cardiac chambers.

2.1 Three-D Cardiac Model

Here we first use 3D biventricular mesh geometry extracted from MRI images, with synthetic myocardial fibres. The active sarcomere force and the passive force are computed at each point of the mesh with the Bestel-Clement-Sorine (BCS) model under the influence of the pre-computed electrophysiology. The boundary condition is a circulation model with the 4 phases of the cardiac cycle based using a 3-parameters Windkessel model of blood pressure as after-load. We also specify a resting mesh in addition of the initial mesh geometry to start the simulation with a geometry which already includes residual stress.

The complete details of the 3D electromechanical model as well as the C++ implementation of the finite element solver are discussed in [5]. With meshes of 10 000 and 15 000 points and a time step of 5 ms, a single beat (around 0.9 s) takes between 25 min and 1 h to compute. Finally, since we want to consider cardiac beats which are not affected by the initialization of the simulation, we compute 3 subsequent beats per simulation and only consider the last one, so the full 3D simulation takes between 75 min and 3 h to be computed.

2.2 0D Cardiac Model

If we then make simplifying assumptions on the geometry and on the properties of the material, by approximating the ventricular shape as a sphere, we can derive the equations of a fast lumped model of the heart as detailed in [6].

The myocardial motion is then only described by the inner radius r of the ventricle (the “Resting Mesh” in 3D becomes simply a “Resting Radius” r0), the material is considered incompressible and has idealised tangential fibres. The electrophysiological activation is supposed synchronous and homogeneous over the sphere as well as the resulting active sarcomere force. Finally we use the same circulation model and Mooney Rivlin equations than in the 3D model.

We implemented the 0D model within the CellML framework, then converted into C code with OpenCOR [7]. With a temporal discretisation of 0.1 ms, we can simulate 10 to 20 heart beats per seconds.

3 Multiscale Coupling

Although with different mechanical assumptions, both models follow the same trends in behaviour when we change the global parameters. The idea of the coupling is to have those trends match within a specific domain of 3D parameters, in order to predict the behaviour of many 3D simulations by only computing 0D simulations. This is done by first matching several 3D simulations of the domain (called the sigma-simulations) with the 0D model, then learning a mapping between the 3D parameters and the 0D parameters.

3.1 Personalisation of the 0D Model to a 3D Simulation

The first step of the coupling is to make the two models match on a single simulated beat. Given one 3D simulated heartbeat, we want to accurately reproduce the pump behaviour of the heart with the 0D model (under the same boundary conditions). In particular we focus on reproducing 6 features of the volume curve by setting 5 main electromechanical parameters in the 0D model, both listed in Table 1.

Table 1. Features and parameters in the 0D model personalisation over a 3D simulation
Full size table

We estimate the parameters by performing a derivative-free optimisation with the genetic algorithm CMA-ES [8]. This powerful algorithm combines Bayesian principles of Maximum Likelihood with a local gradient descent on the members of each generation, by updating at each iteration both an internal covariance Ic and mean Im of the parameters to explore at the next iteration. We define the fitness (score) of each simulation by:

$$\begin{aligned} fitness(x)=||{(Values(x)-TargetValues)/Normalization}||\end{aligned}$$

which is the \(L_2\) distance between the simulated and the objective values, normalized to be able to compare volumes (unit_volume = 10 ml) with times (unit_time = 20 ms), percentages (unit_percent = 5 %) and flow (unit_flow = 10 ml/s).

We use a population of 20 simulations per generation, and optimize over 100 generations. This takes less than 10 min on a multi-core computer with parallel computation of the simulations within each generation. Figure 2 shows the matching behaviours of a 3D simulation and its 0D counterpart.

3.2 Prediction of 3D Behaviour from 0D Simulations

We want to be able to get reliable approximations of other 3D simulations within a domain \(\varOmega _{3D}\) of 3D parameters by doing 0D simulations, so we need to be able to convert a vector \(X\in \varOmega _{3D}\) into a relevant vector Y of 0D parameters which best approximates the 3D simulations. Here we focus in the mapping of \(N_1\)=4 3D parameters toward \(N_2\)=5 0D parameters listed in Table 2.

Fig. 2.
figure 2

Comparison between a volume curve simulated with the 3D model (blue) and the matched 0D simulation (red). Orange lines and points outline the 6 fitted values (Color figure online)

Full size image

The parameters do not behave necessarily the same for both models (and not in the same range of values). For example the 3D and 0D dampings are not calculated in the same way, and the “resting position” variable is a unitless value from 0 to 10 in the 3D case, whereas it is the “inner radius” (in cm) in the 0D mdoel. Also even for parameters coming from the same equations in both models (such as \(\sigma \) and c1) the values might be different for two matching 0D and 3D simulations. For example we can get the same volume curve with contractility and stiffness values which are 10 times smaller in the 0D implementation than in the 3D setting). The mapping is thus not trivial and is done through the following steps:

  1. 1.

    We first perform \(2N_1+1\) 3D simulations at 2 points of each of the \(N_1\) principal directions of the domain of interest \(\varOmega _{3D}\) and its center (called the sigma-simulations with parameters \(S_{i}\)).

  2. 2.

    We then fit the 0D model on each of those \(2N_1+1\) simulations with the method explained in the previous subsection, which gives the \(2N_1+1\) corresponding vectors of 0D parameters \(V_{i}\).

  3. 3.

    Then we compute a least square linear regression \(\phi \) between the parameters of \(S_{i}\) and the parameters \(V_{i}\).

  4. 4.

    Finally for each vector X of \(\varOmega _{3D}\), we get the relevant vector \(Y=\phi (X)\) of 0D parameters by using this linear regression.

3.3 Results of the Parameter Mapping

Here we evaluate the approximation of 80 other 3D simulations with parameters \(X_{j}\in \varOmega _{3D}\) by their corresponding 0D simulations with parameters \(Y_{j}=\phi (X_{j})\). We focus on the error made on 7 features, which we compare with the error made by a direct linear regression between the parameters of the sigma-simulations and the 7 features (which is the best regression model we can run with this small number of points). Results are shown in Table 3.

Both methods provide good approximations of the features. However if we exclude tVmin (which is harder to approximate because of the temporal discretisation of the models), the simulations with the 0D model provide overall better approximations of the values, particularly of those with the most nonlinear behaviour such as the percentage of filling (FVat) and the flow (Qat) when the atrium opens (resp by 43 % and 40 %). This is because the 0D model naturally captures the nonlinear behaviour of those features which would require many simulations to be well approximated by a nonlinear regression model.

4 Efficient Personalisation of the Multiscale Model

Personalisation is the first step for the application of 3D cardiac modelling to patient-specific data. After extracting a patient-specific mesh geometry from the images, we want the 3D simulation to match specific clinical data. This can be done as in Sect. 3.1, by optimizing some parameters of the 3D cardiac model with CMA-ES to minimize a score related to the distance between the simulation and the target clinical data.

Table 2. Three-D and 0D parameters of the mapping
Full size table
Table 3. Feature approximation by the mapping: range of values of each feature, mean absolute error with the mapping (\(MAE_m\)) and mean absolute error with the direct regression (\(MAE_r\))
Full size table

Since the convergence speed of CMA-ES increases with the size of the population evaluated at each iteration, we want to set this size as high as possible, but the computational cost of each 3D simulation is the limiting factor. However with the coupled model, we show that we can evaluate the scores of the members of a large population with a limited number of 3D simulations, which allows to benefit from the increased speed of convergence while keeping a reasonable computational burden.

4.1 Full Personalisation Pipeline

In the personalisation process of the 3D model, we want to reproduce 5 features of the volume curve (listed in Table 4) by optimizing the 4 parameters described in Sect. 3.2. We initialize a CMA-ES optimization process with a high population size m = 80, and derive the Coupled-CMA optimization method by adapting the original CMA-ES as follows:

At each iteration, the CMA-ES algorithm asks for the scores of m 3D simulations \(X_{j}\) whose parameters are drawn from a multivariate distribution, ruled by its own internal mean Im and covariance Ic.

Instead of performing these m 3D simulations, we calculate a mapping \(\phi \) and m surrogate 0D simulations with parameters \(Y_{j}=\phi (X_{j})\), as explained in Sect. 3.2. Only the \(2N_1+1=9\) 3D sigma-simulations are required, which are drawn at the center and within the principal axis of the multivariate distribution (two simulations per axis at ± standard deviation of the axis from the mean).

Table 4. Features and parameters in the 3D model personalisation to a real volume curve
Full size table
Fig. 3.
figure 3

Left: Score per iteration for the 3D methods. Right: Fitting error of each feature for the 34 patients (in percentage of the mean observed value of each feature)

Full size image

Then we calculate the scores of these m surrogate simulations \(Y_{j}=\phi (X_{j})\) and provide the scores to the CMA-ES algorithm “as if” they were the scores of the m 3D simulations.

4.2 Results

In order to compare the efficiency of the Coupled-CMA optimization, we compare it with the full CMA optimization with a population size of 80 (CMA-80), as well as with a direct CMA optimization with a population size of 9 (CMA-9) which has the same computational burden than the Coupled-CMA.

This is done by comparing the scores of the 3D simulations made with the algorithm’s internal mean Im at each iteration, which is the algorithm’s current best estimate of the minimal parameters (In the case of Coupled-CMA, it is the score of the central sigma-simulation). Results are shown in Fig. 3 (left).

The CMA-80 expectedly converges a lot faster than the CMA-9, but the main result is that the Coupled-CMA optimization converges at the same speed than the CMA-80. From a computing viewpoint, the Coupled-CMA lowers the number of 3D simulations from 80 to 9 at each iteration while keeping the accuracy, thus saving between 50 and 150 h of CPU time at each iteration.

This similarity of convergence between CMA-80 and Coupled-CMA was confirmed on other geometries and values to fit, and overall we applied this method to the personalisation of 34 patient hearts, sucessfully matching the features to their target clinical values, within 6 % of the mean value of each feature in the population, for at least 90 % of the cases, as show on Fig. 3 (right).

5 Conclusion

In this manuscript we detailed how a fast reduced “0D” model relying on the same equations but simplifying assumptions can be coupled to the original 3D model to approximate computationally-costly 3D simulations with fast 0D simulations within a domain of 3D parameters. For this we developed a novel method to learn a mapping between the parameters of 3D sigma-simulations within the domain, and the parameters of corresponding 0D simulations with the same mechanical behaviour. In learning how to go from 3D parameters to 0D parameters, we learned the difference between the 0D (lumped) hypothesis and the 3D hypothesis. We then used the coupled model to build a fast personalisation agent, by substituting many 3D simulations in the optimization process by their 0D counterparts. This enabled us to benefit from the higher speed of convergence while considerably reducing the computational burden.

Several aspects of this method can be directly extended to more (nonlinear) features and parameters, such as the pressure, heart rate and the boundary conditions. We could also improve the computational gain by reusing the mapping from one iteration of the CMA-ES to the next one when the domains are similar enough instead of recomputing it. Finally, we expect the personalisation method to scale well to more complex optimization problems with a larger parameter space, since CMA-ES is well suited for those problems.