Hand Pose Estimation from Local Surface Normals

Abstract

We present a hierarchical regression framework for estimating hand joint positions from single depth images based on local surface normals. The hierarchical regression follows the tree structured topology of hand from wrist to finger tips. We propose a conditional regression forest, i.e. the Frame Conditioned Regression Forest (FCRF) which uses a new normal difference feature. At each stage of the regression, the frame of reference is established from either the local surface normal or previously estimated hand joints. By making the regression with respect to the local frame, the pose estimation is more robust to rigid transformations. We also introduce a new efficient approximation to estimate surface normals. We verify the effectiveness of our method by conducting experiments on two challenging real-world datasets and show consistent improvements over previous discriminative pose estimation methods.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

We consider the problem of 3D hand pose estimation from single depth images. Hand pose estimation has important applications in human-computer interaction (HCI) and augmented reality (AR). Estimating the freely moving hand has several challenges including large viewpoint variance, finger similarity and self occlusion and versatile and rapid finger articulation.

Methods for hand pose estimation from depth generally fall into two camps. The first is frame-to-frame model based tracking [1–5]. Model-based tracking approaches can be highly accurate if given enough computational resources for the optimization. The second camp, where our work also falls, is single frame discriminative pose estimation [6–9]. These methods are less accurate than model-based trackers but much faster and are targeted towards real-time performance without GPUs. Model-based tracking and discriminative pose estimation are complementary to each other and there have been notable hybrid methods [10–14] which try to maintain the advantages of both camps.

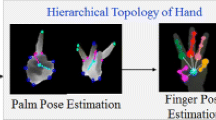
Earlier methods for discriminative hand pose estimation tried to estimate all joints directly [15, 16] though such approaches tend to fail with dramatic view-point changes and extreme articulations. Following the lead of several notable methods [6–8, 10], we cast pose estimation as a hierarchical regression problem. The idea is to start with easier parent parts such as the wrist or palm, and then tackle subsequent and more difficult children parts such as the fingers. The assumption is that the children parts, once conditioned on the parents, will exhibit less variance and simplify the learning task. Furthermore, by constraining the underlying graphical model to follow the tree-structured topology of the hand, hierarchical regression implicitly captures the skeleton constraints and therefore shares some advantages of model-based tracking that are otherwise not present when directly estimating all joints independently.

Our framework starts with estimating the surface normals of given point clouds. The normal direction establishes the local reference frames used in later conditional regression and serves as features. We then apply our Frame Conditioned Regression Forest (FCRF) to hierarchically regress hand joints down from the wrist to the finger tips. At each stage, the frame of reference is established based on previously estimated local surface normal or joint positions. The regression forest considers offsets between input points and joints of interest with respect to the local reference frame and also conditions the feature with respect to these local frames. Our use of conditioned features is inspired by [6], though we consider angular differences between local surface normals, which is far more robust to rigid transformations than the original depth difference feature.

Fig. 1.

Framework. (a) Shows the hand skeleton model used in our work. (b) Sketches our hierarchical regression framework, with each successive stage denoted by a shaded box. We first estimate a reference frame for every input point encoding all information from previous stages and use that reference frame as input to estimate the location of children joints. The sub-figure around the depth map amplifies a local region from the initial depth map and shows the corresponding frame for a specific point. To save space, only thumb and index finger cases are shown and finger tip points (TIP) estimation is omitted as it is identical to that of DIP (best viewed in colour) (Color figure online)

Our proposed method has the following contributions:

• 1. We are the first to incorporate local surface normals for pose estimation. Unlike previous methods [6, 9, 17, 18] based on global geometry, ours is based on local geometry. To this end, we propose an extremely efficient normal estimation method based on regression trees adapted to handle unit vector distributions, different from vector space properties.

• 2. We extend the commonly used depth difference feature [6–8, 10, 17, 18] to an angular difference feature between two normal directions. Our normal difference feature is highly robust to 3D rigid transformation. In particular, the feature is invariant to in-plane rotations, which means we can dispense with data augmentation and have more efficient training and testing routines.

• 3. We propose a flexible conditional regression framework, encoding all previously estimated information as a part of the local reference frame. This includes local point properties such as the normal direction and global properties such as the estimated joint position.

We validate our method on two real-world challenging hand pose estimation datasets, ICVL [7] and MSRA [6]. On ICVL, we achieve the state-of-art performance against all previous discriminative based methods [6–8] with a large margin. On MSRA, our method is on-par with the state-of-art methods [6, 13] at the threshold of 40 mm, and with some minor modifications outperforms [6, 13].

2 Related Works

We limit our discussion to the most relevant issues and works, and refer readers to [19, 20] for more comprehensive reviews on hand pose estimation in general. Hierarchical Regression. Several methods have adopted some form of hierarchical treatment of the pose estimation problem. For example, in [11, 15, 21], the hand is first classified into several classes according to posture or viewpoint; further pose estimation is then conditioned on such initial class. Obviously, such an approach cannot generalize to unseen postures and viewpoints.

Other works [6–10] hierarchically follow the tree-structured hand topology. In [7, 8], data points are recursively partitioned into subsets and only corresponding subsets of points are considered for subsequent joint estimation. In [10], estimated parent joints are used as inputs for regressing children joints; a final energy minimization is applied to refine the estimation. In [6, 9], predictions are made based on previously estimated reference frames. Our work is similar in spirit to [6, 9], as we also make estimations based on reference frames. However, unlike [6, 9], we utilize the normal direction to establish the reference frame and take local point properties into consideration. Further explanations on the differences between our work and [6, 9] are given in Sects. 3.2 and 4.

Viewpoint Handling. The free moving hand can exhibit large viewpoint changes and a variety of techniques have been proposed to handle these. For example, [21, 22] discretize viewpoints into multiple classes and estimate pose in the view-specific classes. Unfortunately, these methods may introduce quantization errors and cannot generalize to unseen viewpoints. In [9], the regression for hand pose is conditioned on an estimated in-plane rotation angle. This is extended in [6], which regresses the pose residual iteratively, conditioned on the estimated 3D pose at each iteration. Such a method is highly sensitive to the pose initialization and may get trapped in local minima.

Point Cloud Features. Depth difference features are widely used together with random forests in body pose [17, 18] and hand pose [6–10, 15, 21] estimation. Depth differences, however, ignore many local geometric properties of the point cloud, e.g. local surface normals and curvatures, and are not robust to rigid transformations and sensor noise.

In [3, 4] geodesic extreme points such as finger tip candidates are used to guide later estimation. Rusu et al. [23] proposed a histogram feature describing different local properties. Inspired by [23], we establish local Darboux frames and using angular differences as feature values, but unlike [23], our features are based on random offsets and retain the efficiency of [17]. Most recently, convolutional neural networks (CNNs) have been used to automatically learn point cloud features [24, 25]. Due to the heavy computational burden, CNNs can still not be used in real-time without a GPU.

3 Random Normal Difference Feature

3.1 Random Difference Features

One of the most commonly used features in depth-based pose estimation frameworks, for both body pose estimation [17, 18] and hand pose estimation [6, 9], is the random depth difference feature [17]. Formally, the random difference feature $f_{\mathcal {I}}$ for point $\mathbf {p}_i \in \mathcal {R}^3$ from depth map $\mathcal {I}$ is defined as follows,

$$\begin{aligned} f_{\mathcal {I}}(\mathbf {p}_i, \mathbf {\delta }_1, \mathbf {\delta }_2) = \varDelta (\phi _{\mathcal {I}}(r(\mathbf {p}_i, \mathbf {\delta }_1)), \phi _{\mathcal {I}}(r(\mathbf {p}_i, \mathbf {\delta }_2))), \end{aligned}$$

(1)

where $\mathbf {\delta }_j \in \mathcal {R}^3, j=\{1,2\}$ is a random offset, $r(\mathbf {p}_i, \mathbf {\delta }_j) \in \mathcal {R}^3$ calculates a random position given point $\mathbf {p}_i$ and offset $\mathbf {\delta }_j$. $\phi _{\mathcal {I}}(\mathbf {q})$ is the local feature map for position $\mathbf {q}\in \mathcal {R}^3$ on the point cloud and $\varDelta (\cdot , \cdot )$ returns the local feature difference. In the case of random depth difference features [6, 9, 17], $\phi _{I}$ is the recorded depth, though the same formalism applies for other features.

Random difference features are well suited for random forest frameworks; the many possible combinations of offsets perfectly utilize their feature selection and generalization power. In addition, every dimension of the feature is calculated independently, which gives rise to parallelization schemes and allows for both temporal and spatial efficiency in training and testing. One of the main drawbacks of the depth-difference feature, however, is its inability to cope with transformations. Since random offsets in $r(\mathbf {p}_i, \mathbf {\delta }_1)$ are determined either w.r.t. the camera frame [17] or to a globally estimated frame [6, 9], the depth difference for the same offset can vary widely under out of plane rotations.

3.2 Pose Conditioned Random Normal Difference Feature

Surface normals are an important local feature for many point-cloud based applications such as registration [23] and object detection [26–28]. Surface normals would seem a good cue for hand pose estimation too, since the direction of the surface helps to establish the local reference frame, as will be described in Sect. 4. For two given points, the angular difference between their normal directions remains unchanged after rigid transformations. Hence, we propose a pose-conditioned normal difference feature which is highly robust towards 3D rigid transformations.

To make random features invariant to 3D rigid transformations i.e.,

$$\begin{aligned} f_{\mathcal {I}}(\mathbf {p}_i, \mathbf {\delta }_1, \mathbf {\delta }_2) = f_{\mathcal {I}'}(\mathbf {p}'_i, \mathbf {\delta }_1, \mathbf {\delta }_2), \end{aligned}$$

(2)

where $\mathcal {I'}$ and $\mathbf {p'}_i \in \mathcal {R}^3$ are the depth map and point position after transformation, it is necessary to satisfy the following two conditions:

 

i:

The random offset generator $r(\cdot , \cdot )$ should be invariant to rigid transformations, i.e. 

$$\begin{aligned} T(r(\mathbf {p}_i, \mathbf {\delta }_j)) = r(T(\mathbf {p}_i), T(\mathbf {\delta }_j)), \end{aligned}$$

(3)

where $T(\mathbf {q}) = \mathbf {R}\cdot \mathbf {q} + \mathbf {t}$ is the rigid transformation with $\mathbf {R} \in \text{ SO(3) }$ ¹ and $\mathbf {t}$ as its rotation and translation respectively. This condition is equivalent to guaranteeing that the relative position between $\mathbf {p}_i$ and $r(\mathbf {p}_i, \mathbf {\delta }_j)$ remains unchanged after transformation, i.e., $T(\mathbf {p}_i - r(\mathbf {p}_i, \mathbf {\delta }_j)) = T(\mathbf {p}_i) - r(T(\mathbf {p}_i), T(\mathbf {\delta }_j))$.

ii:

The feature difference $\varDelta (\cdot , \cdot )$ should be invariant to rigid transformation, i.e. 

$$\begin{aligned} \varDelta (\phi _{\mathcal {I}}(\mathbf {q}_1), \phi _{\mathcal {I}}(\mathbf {q}_2)) = \varDelta (\phi _{\mathcal {I'}}(\mathbf {q'}_1), \phi _{\mathcal {I}}(\mathbf {q'}_2)), \end{aligned}$$

(4)

where $\mathbf {q}_j'= T(\mathbf {q}_j), j\in \{1,2\}$ is the transformed offset position.

 

To meet condition i, we extend the random position calculation $r(\mathbf {p}_i, \mathbf {\delta }_j)$ as

$$\begin{aligned} r(\mathbf {p}_i, \mathbf {\delta }_j, \mathbf {R}_i) = \mathbf {p}_i + \mathbf {R}_i\cdot \mathbf {\delta }_j, \end{aligned}$$

(5)

where $\mathbf {R}_i \in \text{ SO(3) }$ is a latent variable representing the pose of local reference frame Sect.4. For any rigid transformation $\mathbf {T} = \begin{bmatrix} \overline{\mathbf {R}}&\overline{\mathbf {p}} \\ 0&1 \end{bmatrix}$, Eq. 5 satisfies condition i iff

$$\begin{aligned} \mathbf {R}'_i = \overline{\mathbf {R}}\mathbf {R}_i, \end{aligned}$$

(6)

where $\mathbf {R}_i$ and $\mathbf {R}'_i$ are the estimated latent variable before and after rigid transformation respectively. In comparison to [6], which also uses a latent variable $\mathbf {R}$, the $\mathbf {R}$ is estimated globally and therefore can be sensitive to the initialization. For us, the local Darboux frame is established through the local surface normal direction (see Sect. 5) and has no such sensitivity.

To meet condition ii, given the random positions $\mathbf {q}_1$ and $\mathbf {q}_2$, we use the direction of the normal vector as our local feature map. The feature difference is cast as the angle between two normals, i.e. 

$$\begin{aligned} \varDelta (\phi _{\mathcal {I}}(\widetilde{\mathbf {q}_1}), \phi _{\mathcal {I}}(\widetilde{\mathbf {q}_2})) = n(\widetilde{\mathbf {q}_1})\cdot n(\widetilde{\mathbf {q}_2}), \end{aligned}$$

(7)

where $\widetilde{q}$ denotes the 2D projection of the random position onto the image plane, since the input 2.5D point cloud is indexed by the 2D projection coordinates. $n(\cdot )\in \mathcal {R}^3$ denotes the corresponding normal vector. Since the angle between two normal vectors remains unchanged under a rigid transformation for any two given surface points, our feature also fulfills condition ii. In comparison, the depth difference feature, as used in [6, 9, 17], does not fulfill this condition.

Our proposed normal difference feature can be computed based on any surface normal estimate. We describe a conventional method based on eigenvalue decomposition in Sect. 3.3 and then propose an efficient approximation alternative in Sect. 3.4.

Fig. 2.

Estimated surface normal. From (a) to (c) the x, y, z-axis coordinate of the normal vector, resp. The first row is the regressed surface normal by the random forest and the second row is estimated by PCA. (Best viewed in colour) (Color figure online)

3.3 Surface Normal Estimation Based on Eigenvalue Decomposition

For an input 2.5D point cloud, we distinguish between inner points that lie inside the point cloud and edge points on the silhouette of the point cloud. For edge points, normal estimation degenerates to 2D curve normal estimation since the normal direction is constrained to lie in the image plane.

For inner points, the local surface can be approximated by the k-neighbourhood surface direction [26]. The eigenvector corresponding to the smallest eigenvalue of the neighbourhood covariance matrix can be considered the normal direction. The sign of the normal direction is further constrained to be the same as the projection ray.

3.4 Surface Normal Regression with Random Forests

Estimating the normal at every inner point in the point cloud can become very computationally expensive, with an eigenvalue decomposition per point. Alternatively, we can take advantage of the efficiency of random forests and regress an approximate normal direction. Directly regressing the normal vectors in vector space does not maintain unit length so we parameterize the normal vector with spherical coordinates $(\theta , \varphi )$ where $\theta$ and $\varphi$ are the polar and azimuth angles, resp. $\theta$ and $\varphi$ are independent and can be regressed separately. We model the distribution of a set of angular values $\mathcal {S} = \{\theta _1, \cdots \theta _n \}$ as a Von Mises Distribution, which is the circular analogue of the normal distribution. The distribution is expressed as

$$\begin{aligned} p_{VM}(\theta _i | \mu , \kappa ) = \frac{e^{\kappa cos(\theta _i-\mu )}}{2\pi I_0({\kappa })}, \end{aligned}$$

(8)

where $\mu$ is the mean of the angles, $\kappa$ is inversely related to the variance of the approximated Gaussian and $I_0({\kappa })$ is the modified Bessel function of order 0. To estimate the mean and variance of the distribution, we first define

$$\begin{aligned} \overline{C} = \sum _{i}\cos (\theta _i),~ \overline{S} = \sum _{i}\sin (\theta _i),~ \overline{R} = (\overline{C}^2 + \overline{S}^2)^{\frac{1}{2}}. \end{aligned}$$

(9)

Then the maximum likelihood estimates of $\mu$ and $\kappa$ are

$$\begin{aligned} \mu = \text{ atan2 }(\overline{S}, \overline{C}) \qquad \text {and} \qquad \overline{R} = \frac{I_1({\kappa })}{I_0({\kappa })}. \end{aligned}$$

(10)

During training, each split node is set by maximizing the information gain as

$$\begin{aligned} I = H(\mathcal {S}) - \sum _{i\in \{L,R\}}\frac{|\mathcal {S}^i|}{|\mathcal {S}|}H(\mathcal {S}^{i}), \end{aligned}$$

(11)

where the entropy of the Von Mises Distribution is defined as

$$\begin{aligned} H(\mathcal {S}) = \text{ ln }(2\pi I_0(\kappa )) - \kappa \frac{I_1({\kappa })}{I_0({\kappa })}. \end{aligned}$$

(12)

The training procedure for the random forest that estimates the normal is almost identical to [17] with the exception that the random offsets are restricted to lie within the region of the same k-nearest neighbourhood that was used for the eigenvalue decomposition based normal estimation in Sect. 3.3. The mean of the angular values propagated to each leaf node is selected as the leaf node’s prediction value. In practice, to make the normal regression even more efficient, we combine the estimation of $\theta$ and $\varphi$ into one forest by regressing the $\theta$ in the first 10 layers and $\varphi$ in the later 10 layers, rather than estimating them independently.

Since the random offset is limited to a small area, which restricts the randomness of the trees, we find that the average error between approximated and true normal directions only goes up from $\sim \!\!12^{ \circ }$ to $\sim \!\!14^{ \circ }$ when decreasing the number of trees from 10 to 1. As the normal difference feature is not sensitive to such minor errors, we use only 1 tree for all experiments in this paper. The proposed method is extremely efficient; normals for input point clouds can be estimated in $\sim \!\!4$ ms on average, compared to $\sim \!\!14$ ms based on eigenvalue decompositions on the same machine.

4 Frame Conditioned Regression Forest

We formulate hand joint estimation as a regression problem by regressing the 3D offsets between an input 3D point and a subset of hand joints. Directly regressing all joints of the hand at once, as has been done in previous works [15, 16] is difficult, given the highly articulated nature of the hand and the many ambiguities due to occlusions and local self-similarities of the fingers. Instead, we prefer to solve for the joints in a hierarchical manner, as state-of-the-art results [6, 10] have demonstrated the benefits of solving the pose progressively down the kinematic chain.

In this section, we propose a conditional regression forest, namely the Frame Conditioned Regression Forest (FCRF) which performs regression conditioned on information estimated in the previous stages. The hand joints are regressed hierarchically by following the kinematic chain from wrist down to the finger joints. At each stage, we first estimate the reference frame based on results of previous stages and then regress the hand joints relevant to that stage with the FCRF.

There are three main benefits to using the FCRF. First of all, offsets between input points and finger joints are transformed into the local reference frame. This reduces the variance of the offsets and simplifies the training. It also implicitly incorporates skeleton constraints provided by the training data. Secondly, the related normal difference feature, as described in Sect. 3, is conditioned on the estimated reference frame and makes the joint regression highly robust to 3D rigid transformations. Finally, FCRF is in-plane rotation-invariant, and does not need manually generated in-plane rotated training samples for training as in [6–8], so the training time and resulting tree size can be reduced significantly.

Specifically, given input point $\mathbf {p}_i \in \mathcal {R}^3$ from the point cloud, the FCRF for the $j^\text {th}$ stage solves the following regression

$$\begin{aligned} \mathbf {O}_{j}^{(i)} = r_{j}(\mathcal {I}, \mathbf {C}_{j}^{(i)}), \end{aligned}$$

(13)

where $\mathbf {O}_{j}^{(i)} \in \mathcal {R}^{3\times n}$ is the offsets between input point $\mathbf {p}_i$ and the n joints to be estimated in $j^\text {th}$ stage, $\mathcal {I}$ denotes the input depth map and $\mathbf {C}_{j}^{(i)} \in \text{ SE(3) }$ is the corresponding local frame. We define the position of the input point $\mathbf {p}_i$ as the origin of the local reference frame, i.e. 

$$\begin{aligned} \mathbf {C}_{j}^{(i)} = \left[ \begin{array}{c|c} \mathbf {R}_{j}^{(i)} &{} \mathbf {p}_i \\ \hline 0 &{} 1 \end{array} \right] , \end{aligned}$$

(14)

where $\mathbf {R}_{j}^{(i)} = \begin{bmatrix}\mathbf {x}, \mathbf {y}, \mathbf {z}\end{bmatrix}\in \text{ SO(3) }$ is a rotation matrix representing the frame pose, and $\mathbf {x},\mathbf {y},\mathbf {z}\in \mathcal {R}^3$ are the corresponding axis directions. Both $\mathbf {R}_i$ and $\mathbf {p}_i$ are defined with respect to the camera frame.

The regression $r_j(\mathcal {I}, \mathbf {C}_{j}^{(i)})$ is done by a random forest.

During training, $\mathbf {o}_{ik} \in \mathcal {R}^3$, the offset between point $\mathbf {p}_i$ and joint $\mathbf {l}_k$ to be estimated, is first rotated to the local reference frame $\mathbf {C}_j^{(i)}$ as $\widetilde{\mathbf {o}_{ik}}$, i.e. 

$$\begin{aligned} \widetilde{\mathbf {o}_{ik}} = (\mathbf {R}_j^{(i)})^{T}\cdot \mathbf {o}_{ik}. \end{aligned}$$

(15)

The distribution of offset samples are modeled as a uni-modal Gaussian as in [17]. For each split node of the tree, the normal difference feature which results in the maximum information gain from a random subset of features is selected. For each leaf node, mean-shift searching [29] is performed and the maximal density point is used as the leaf prediction value.

During testing, given the estimated local frame $\mathbf {C}_j^{(i)}$, the resulting offset $\mathbf {o}_{ik}$ can be re-projected to the camera frame as

$$\begin{aligned} \mathbf {o}_{ik} = (\mathbf {R}_j^{(i)})\cdot \widetilde{\mathbf {o}_{ik}}. \end{aligned}$$

(16)

5 Hierarchical Hand Joint Regression

In this section, we detail the design of reference frames used by FCRFs in every stage, given the estimated local surface normal and the parent joint positions from previous stages. Free moving hand pose estimation faces two major challenges, i.e., large variations of viewpoints, and self-similarities of different fingers. We decompose hand pose estimation into two sub-problems that explicitly tackle these two challenges: first, we estimate the reference frame of the palm and second, we estimate the finger joints.

In Sects. 5.1 and 5.2 the palm estimation is introduced by first estimating the wrist joint (palm position) followed by MCP joints (Fig. 1(a)) for all 5 fingers (palm pose), in which the Darboux frame for every input point is established by taking the estimated wrist joint as reference point. In Sects. 5.3 and 5.4 the joints for each finger are estimated, progressively conditioned on the previously estimated joint position.

5.1 Wrist Estimation

We consider only edge points on the hand silhouette as inputs for estimating the wrist joint. Our rationale is that we cannot find unique reference frames for non-edge points, since knowing only the direction of the normal, i.e. the z-axis, is insufficient to uniquely determine the x- and y-axis on the tangent plane. We assume orthographic projection for the point cloud, i.e. the tangent plane of edge point is orthogonal to the image plane, then the local reference frame of edge point $\mathbf {p}_i$ can be defined uniquely as follows,

$$\begin{aligned} \begin{aligned} \mathbf {x}_{wrist}^{(i)} = \mathbf {n}, \mathbf {y}_{wrist}^{(i)} = \mathbf {z}_{wrist}^{(i)} \times \mathbf {x}_{wrist}^{(i)}, \mathbf {z}_{wrist}^{(i)} = \mathbf {n}_i, \end{aligned} \end{aligned}$$

(17)

where n is the image plane normal direction, $\mathbf{n}_i$ is the normal to the silhouette at point i. The resulting local reference frame is not only invariant to 2D rotations in the image plane but to some degree also robust to out-of-plane rotations, provided that the hand silhouette does not change too much.

5.2 Metacarpophalangeal (MCP) Joint Estimation

Given the estimated wrist point position as a reference point, we assume its relevant position under the local frame $C_{MCP}^{(i)}$ is unchanged then the local reference frame for point $\mathbf {p}_i$ is established as follows

$$\begin{aligned} \begin{aligned} \mathbf {x}_{MCP}^{(i)} = \mathbf {y}_{MCP}^{(i)}\times \mathbf {z}_{MCP}^{(i)}, \mathbf {y}_{MCP}^{(i)} = \frac{\mathbf {n}_i\times (\mathbf {p}_{wrist}-\mathbf {p}_i)}{\Vert \mathbf {n}_i\times (\mathbf {p}_{wrist}-\mathbf {p}_i)\Vert _{2}}, \mathbf {z}_{MCP}^{(i)} = \mathbf {n}_i, \end{aligned} \end{aligned}$$

(18)

where the z-axis of the local reference frame is defined as the normal direction $\mathbf {n}_i$, and the y-axis is defined by taking the wrist location $\mathbf {p}_{wrist}$ as a reference point. The MCP joints from all five fingers are then regressed simultaneously, i.e., $\mathbf {O}_{MCP}^{(i)} \in \mathcal {R}^{3\times 5}$ using our previously defined FCRF.

The estimated MCP joints are then replaced by the transformed MCP position from a template palm to reduce the accumulated regression error. We first find a closed form solution of the palm pose using a variation of ICP [30]. The palm pose matrix $\mathbf {R}_{palm}$’s y-axis is defined as the direction from the wrist to the MCP joint of the middle finger, the z-axis is defined as the palm normal.

5.3 Proximal Interphalangeal (PIP) Joint Estimation

In the estimation of the PIP joint for finger k, all input reference frames share the same pose as the rotated palm reference frame as follows,

$$\begin{aligned} \mathbf {C}_{PIP_{k}}^{(i)} = \left[ \begin{array}{c|c} \text{ Rot }_k(\mathbf {R}_{palm}) &{} \mathbf {p_i} \\ \hline 0 &{} 1 \end{array} \right] , \end{aligned}$$

(19)

where $\text{ Rot }_k(\cdot )$ is an in-plane rotation to align the reference frame’s y-axis to the $k-^\text {th}$ finger’s empirical direction Fig. 1(a).

Given the local self-similarity between fingers, it can be easy to double-count evidence. To avoid this, we adopt two simple measures. First, we use points only from the neighbourhood of the parent MCP joint as input for regressing each PIP joint, since these points best describe the local surface distortion raised by the parent joint articulation [31]. Secondly we limit the offset of the FCRF to lie along the direction of the finger to maintain robustness to noisy observations from nearby fingers.

5.4 Distal Interphalangeal Joint (DIP) and Finger Tip (TIP) Estimation

The ways to estimate DIP and TIP joints are identical, since their parents are both 1-DoF joints. The local reference frame for each joint is defined as follows

$$\begin{aligned} \begin{aligned} \mathbf {x}_l= \mathbf {z}_{palm}\times \mathbf {y}_l, \mathbf {y}_l = \mathbf {p}(l)-\mathbf {g}(l), \mathbf {z}_l = \mathbf {x}_l\times \mathbf {y}_l, \end{aligned} \end{aligned}$$

(20)

where $\mathbf {z}_{palm}$ is the normal direction of palm, $\mathbf {p}(l)$ and $\mathbf {g}(l) \in \mathcal {R}^3$ denote the parent and grandparent joint of l respectively. To avoid double counting of local evidence, we adopt the same techniques as in Sect. 5.3.

6 Experiments

We apply our proposed hand estimation method to two publicly available real-world hand pose estimation datasets: ICVL [7] and MSRA [6]. The performance of our method is evaluated both quantitatively and qualitatively. For quantitative evaluation, two evaluation metrics, per-joint error (in mm) averaged over all frames and percentage of frames in which all joints are below a threshold [18], are used. We show qualitative results in Fig. 5.

All experiments are conducted on an Intel 3.40 GHz I7 machine and the average run time is 29.4 fps or 33.9 ms per image. The maximum depth of all the trees is set to 20. The number of trees for all joint regression forests are set to 5 and 1 for normal estimation (see Sect. 3.4).

To highlight the effectiveness of our proposed normal difference feature, we first apply our frame conditioned regression forests with the same hierarchical structure but based on the standard depth difference feature [17]. We denote this variation using the depth difference feature as our baseline method. It should be noted that the baseline does depend on normal estimation for the establishment of the local wrist frame. We also compare to methods directly regressing the wrist and MCP joint positions without establishing the frame [7, 8] or based on an initial guess and the subsequent, iterative regression of the error [6].

6.1 ICVL Hand Dataset

The ICVL hand dataset [7] has 20 K images from 10 subjects and an additional 160K in-plane rotated images for training. Since our method is invariant to in-plane rotation, we train with only the initial 20 K. The test set is composed of 2 sequences with continuous finger movement but little viewpoint change.

Fig. 3.

Quantitative evaluation on ICVL dataset. From (a) to (c), success rates over different thresholds on sequence A, B and both respectively. (d) pre-joint average error on both sequences (R:root, T:tip)

We compare our method (both the baseline and the version with the normal difference feature) against the state-of-art methods Latent Regression Forest (LRF) [7], Segmentation Index Points (SIP) [8], and Cascaded Regression (Cascaded) [6]. Figure 3(a)–(c) shows that both variations of our proposed method outperform LRF [7] and SIP [8] by a large margin on both test sequences. In comparison to the Cascaded method of [6], shown in Fig. 3(c), our baseline is comparable or better at almost all allowed distances, while the variation with the normal difference feature boosts performance by another 5–10%. As shown in Fig. 3(d), our method significantly out-performs [7], and it outperforms [6] by $\sim \!\!2$ mm in terms of the mean error. These results confirm that conditioning finger localization on the wrist pose, as we have done and as is done in [6], can significantly boost accuracy. Furthermore, our proposed normal difference feature is able to better handle 3D rigid transformations.

6.2 MSRA Hand Dataset

The MSRA hand dataset [6] contains 76.5 K images from 9 subjects with 17 hand gestures. We use a leave-one-subject-out training/testing split and average the results over the 9 subjects. This dataset is complementary to the ICVL dataset since it has much larger viewpoint changes but limited finger movements. The sparse gesture set does not come close to reflecting the range of hand gestures in real-world HCI applications and as such, is not suitable for evaluating how well a method can generalize towards unseen hand gestures. Yet, this dataset is very good for evaluating the robustness of pose estimation methods to 3D rigid transformations; for HCI applications, this offers flexibility for mounting the camera in different locations.

Fig. 4.

Quantitative evaluation on MSRA dataset. (a) to (b): average joint error as a function of pitch and yaw angle of the palm pose with respect to camera frame; (c) success rates over different thresholds.

As is shown in Fig. 4(a)–(b), using the normal difference exhibits less variance to viewpoint changes than using the depth difference. This is more prominent in the pitch angle due to the elongated hand shape. For a given pair of points, their depth difference exhibits larger variation w.r.t. pitch angle viewpoint changes. Nevertheless, the performance of the normal difference does decrease under large viewpoint changes. We attribute this to the errors in surface normal estimation due to point cloud noise and to the fact that a 2.5D point cloud only partially represents the full 3D surface.

We compare our proposed method against the state-of-the-art Cascaded Regression (Cascaded) [6] and the Collaborative Filtering (Filtering) [13] approaches. Above an allowed distance of 40 mm to the ground truth, our approach is comparable to the others. Below the 40 mm threshold, our baseline and the normal difference feature version has around $\sim \!\!14\,\%$ less frames than competing methods. We attribute the difference to the fact that both the Cascaded and the Filtering approach consider the finger as a whole, in the former case for regression, and in the latter as a nearest neighbour search from the training data. While our method generalizes well to unseen finger poses by regressing each finger joint progressively, it is unable to utilize the sparse (albeit similar to testing) set of finger poses in the training. Nevertheless, in an HCI scenario, a user is often asked to first make calibration poses which are important to improve accuracy. As such, we propose two minor modifications to make more comparable evaluations.

For the first modification, we first regress the palm pose, normalize the hand, and then classify the hand pose as a whole. Based on the classification, we assign a corresponding pose sampled from the training set, transformed accordingly to the palm pose. This modification, which we denoted as pose classification is similar to Filtering [13] as both methods consider the hand as a whole. By classifying the 17 gesture classes as provided by the MSRA dataset we now outperform [13] over a large interval of thresholds larger than 22 mm. We attribute the increased performance to our accurate estimate of the palm pose.

For the second modification, we regress each finger (i.e. the 3 finger joints PIP, DIP, TIP) as a whole given the estimated palm pose. This is similar in spirit to the regression strategy in [6] which takes each finger as a whole. Our method outperforms [6] by $\sim \!\!5\,\%$ in the 25–30 mm threshold interval. We attribute this improvement to our palm pose estimation scheme which avoids sensitivity to initialization [6].

Despite our modifications, it should be noted that regressing the finger as a whole cannot generalize to unseen joint angle combinations for one finger, which is usually the case in real-world HCI scenarios, e.g. grasping a virtual object, where one finger may exhibit various joint angle combinations according to the shapes of different objects. However, the two strategies are complementary, i.e. regressing finger joints progressively can generalize to unseen finger poses while regressing the finger as a whole can capture finger joint correlations in training samples. Given enough computational resources, the two strategies can be performed in parallel, with the best estimation being selected according to an energy function as in model-based tracking. We leave this as our future work.

Fig. 5.

Examples of successful and failed pose estimates on the ICVL [7] and the MSRA [6] dataset. Failures are due to extreme view point, wrongly estimated normal direction, etc. (best viewed in colour) (Color figure online)

7 Conclusion and Future Work

We have presented a hierarchical regression scheme conditioned on local reference frames. We utilize the local surface normal both as a feature map for regression and to establish the local reference frame. We also proposed an efficient surface normal estimation method based on random forests. Our system shows excellent results on two real-world, challenging datasets and is either comparable or outperforms state-of-the-art methods in hand pose estimation.

The surface normal serves as an important local property of the point cloud. While random forests are an efficient way of estimating the normal, they are only one way and other methods could be developed to be more accurate. Given the success of using surface normals in our work, we expect that there will be benefits for model-based tracking as well.

In our current work, we follow a tree-structured model of the hand. Given the flexibility of our proposed conditioned regression forest, one can also perform hierarchical regressions with other underlying graphical models. With different models, one could take into account the correlations and dependencies between fingers, especially with respect to grasping objects. We leave this as future work in improving the current system.