All-Around Depth from Small Motion with a Spherical Panoramic Camera

Abstract

With the growing use of head-mounted displays for virtual reality (VR), generating 3D contents for these devices becomes an important topic in computer vision. For capturing full 360 degree panoramas in a single shot, the Spherical Panoramic Camera (SPC) are gaining in popularity. However, estimating depth from a SPC remains a challenging problem. In this paper, we propose a practical method that generates all-around dense depth map using a narrow-baseline video clip captured by a SPC. While existing methods for depth from small motion rely on perspective cameras, we introduce a new bundle adjustment approach tailored for SPC that minimizes the re-projection error directly on the unit sphere. It enables to estimate approximate metric camera poses and 3D points. Additionally, we present a novel dense matching method called sphere sweeping algorithm. This allows us to take advantage of the overlapping regions between the cameras. To validate the effectiveness of the proposed method, we evaluate our approach on both synthetic and real-world data. As an example of the applications, we also present stereoscopic panorama images generated from our depth results.

1 Introduction

For virtual reality (VR) purpose, monoscopic 360$^{\circ }$ videos are currently the most commonly filmed contents. Major electronic companies are constantly launching new VR head-mounted displays [1–3] to further immerse users into VR contents. For capturing 360$^{\circ }$ scenes, cheap and compact Spherical Panoramic Cameras (SPC) equipped with two fisheye lenses, are gaining in popularity.

Only two types of omnidirectional imaging sensor have the ability to capture a full 360$^{\circ }$ image. The first possibility is to employ a panoramic catadioptric camera [4, 5]. A catadioptric camera is the association of a perspective camera with a convex mirror whose shapes are conic, spherical, parabolic or hyperbolic. This layout requires complex optics which incurs a loss of resolution. However, such type of camera can be cost-effective since a single camera is sufficient to cover the whole scene [6, 7]. The second type of spherical sensors are called polydioptric cameras, with such sensors, images captured from multiple cameras are stitched to form a single spherical image. This bulky architecture allows to obtain a high resolution panoramic image, but is relatively expensive. To balance the advantage of the cost efficiency and image quality, some companies have recently released spherical panoramic cameras (SPCs) [8–10] (see Fig. 1). The SPC consists of two fisheye cameras (covering a field of view of 200$^{\circ }$ each) staring at opposite directions.

Several 3D reconstruction algorithms [11, 12] involving omnidirectional cameras have been developed for VR applications. However, these methods are effective only when the input images contain large motions. For the practical uses, one interesting research direction is depth estimation from a small-motion video clip captured by off-the-shelf cameras, such as DSLRs or mobile phone cameras [13–15]. Although these approaches achieve competitive results, they have not been applied to spherical sensors.

Fig. 1.

Spherical panoramic cameras (Ricoh Theta S, Samsung Gear 360 and LG 360)

Fig. 2.

Stereoscopic panorama generation from small motion.

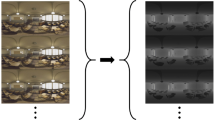
In this paper, we present an accurate dense 3D reconstruction algorithm using small baseline image sequences captured by a SPC as shown in Fig. 2. To achieve this, we design a novel bundle adjustment which minimizes the residuals directly on the unit sphere and estimates approximated-metric depth as well as camera poses; this approach is presented in Sect. 3.2. In order to estimate the all-around depth map, we propose a novel sphere sweeping algorithm in Sect. 3.3. This approach utilizes both the frontal and rear cameras for taking advantage of overlapping regions. The qualitative and quantitative results in Sect. 4 demonstrate that the proposed framework generates highly accurate depth of the entire surrounding scene. Using the accurate depth map, we also show realistic 3D panoramas which are suitable for VR devices (Sect. 4.4).

2 Related Work

The related work can be divided in two categories: the 3D reconstruction from small baseline images and the depth estimation from fisheye cameras.

Structure from Small Motion. Structure from Small Motion (SfSM) have recently been spotlighted [13–17]. These approaches require 2 steps; the camera poses estimation and the dense 3D reconstruction. A simplified version of this framework has been presented in [16] where the dense 3D reconstruction is computed using a sequence of images captured by a linearly moving DSLR camera mounted on a rail. To do so, the authors developed an approach inspired by light-field cameras. The 3D reconstruction method designed for unstructured small motions have been proposed by Yu and Gallup in [13]. This novel method relies on the small angle approximation and inverse depth computation. Therefore, their bundle adjustment is initialized with zero motion and random depths. After bundle adjustment, the dense depth map is computed using a plane sweeping algorithm [18] and a MRF optimization. Other improvements of this method have been developed, for instance, in [14], Im et al. designed a new bundle adjustment for rolling shutter cameras. More recently, Ha et al. [15] presented a framework for uncalibrated SfSM and proposed a plane sweeping stereo with a robust measure based on the variance of pixel intensity.

3D Reconstruction Using Fisheye Cameras. Although omnidirectional cameras have been extensively used for sparse 3D reconstruction and SLAM [11, 19–23], estimating the dense depth map from the fisheye cameras remains a challenging problem. For this particular problem, Li [24] presented a fisheye stereo method, where the author reformulated a conventional stereo matching scheme for binocular spherical stereo system using the unified spherical model. Kim and Hilton [25] also proposed a stereo matching method for a fisheye stereo camera, where a continuous depth map is obtained from a partial differential equation optimization. Meanwhile, Hane et al. [12] presented a real-time plane-sweeping algorithm which is suitable for images acquired with fisheye cameras.

In this paper, we combine these two concepts for SPCs. This configuration is more challenging than the previous methods due to the sensor characteristics. Thus, the ultimate goal of this work is to estimate an accurate and dense depth map using a unified optimization framework designed for weakly overlapping dual fisheye camera system. We show the details of our method in the next section.

3 All-Around Depth from Small Motion

To capture our dataset we used a Ricoh Theta S (see Fig. 1(a)). This sensor is a consumer device which has the advantage to be cheap and compact. Each fisheye camera has a field of view of approximatively 200$^{\circ }$. Therefore, a small overlapping region is still available, this extra information is taken into consideration in our technique in order to obtain a better estimation of the depth at the boundary regions of the image. Another advantage of using this dual fisheye sensor is that the both images are captured simultaneously on the same imaging sensor thanks to a clever design involving mirrors and prisms (see Fig. 4). Thus, the images are always acquired simultaneous without requiring an external electronic trigger.

Fig. 3.

Illustration on bundle adjustment variables

The goal of the proposed method is to estimate an all-around dense depth map from a 360$^{\circ }$ spherical video clip with small viewpoint variations for realistic stereoscopic applications. Our method consists of two steps: (1) a bundle adjustment (BA) for camera pose estimation along with a sparse 3D reconstruction, and (2) a sphere sweep stereo for dense depth map estimation. Our method differs from the prior works [13–15] by its adaptation to the unified spherical camera model making our approach very versatile (compatible with any single viewpoint camera). Furthermore, we propose a novel formulation of the dense matching which takes overlapping regions into consideration. The details of these techniques are explained in the following sections.

3.1 Unified Omnidirectional Camera Model

The spherical model allows us to represent the projection of any single view-point cameras thanks to a stereographic projection model [26–29]. Indeed, the image formation process for any central camera can be expressed by a double projection on a unit sphere (see Fig. 3). Firstly, the 3D point $\mathbf {X}(X,Y,Z)$ is projected on a camera-centered unit sphere $\hat{\mathbf {X}} = \mathbf {X}/ \Vert \mathbf {X} \Vert$. Then, the point $\hat{\mathbf {X}}(\hat{X},\hat{Y},\hat{Z})$ is projected onto the image plane at the pixel coordinates $\mathbf {u}(u,v,1)$. The distance between the unit sphere center $C_{s}$ and the shifted camera center $C_{c}$ is defined as $\xi$, which maps the radial distortion on the image. According to [29], the projection $\hbar (\mathbf {X})$ of a 3D point onto the normalized image coordinates $\mathbf {x}(x,y,1)$ can be expressed as follows:

$$\begin{aligned} \mathbf {x}=\mathbf {K}^{-1}\mathbf {u} = \hbar (\mathbf {X}) = \left[ \begin{matrix} X/(Z+||\mathbf {X}||\xi ) \\ Y/(Z+||\mathbf {X}||\xi ) \\ 1 \end{matrix} \right] , \end{aligned}$$

(1)

where $\mathbf {K}$ is the intrinsic matrix that contains the focal lengths $f_x,\ f_y$, the skew parameter $\alpha$ and the principal point coordinates $c_x,\ c_y$. The back-projection from the normalized image coordinates to the world coordinates is also an essential relationship which can be written as:

$$\begin{aligned} \mathbf {X}=\hbar ^{-1}(\mathbf {x}, w) = \frac{1}{w}\left( \frac{\xi +\sqrt{1+(1-\xi ^2)(x^2+y^2)}}{x^2+y^2+1}\left[ \begin{matrix} x \\ y \\ 1 \end{matrix} \right] -\left[ \begin{matrix} 0 \\ 0 \\ \xi \end{matrix} \right] \right) , \end{aligned}$$

(2)

where w is the inverse depth such that $w = \frac{1}{\Vert \mathbf {X}\Vert }$.

3.2 Bundle Adjustment

In this section, we introduce our bundle adjustment tailored for a SPC consisting of two fisheye cameras looking at opposite directions. The input of our approach is a short video clip where each frame is a concatenated image of the two simultaneous fisheye camera images, the average image of an input clip is shown in Fig. 4(a). For the sake of convenience, we consider the left and right images separately, and name them, respectively, frontal and rear camera.

Fig. 4.

The 3D point cloud and camera poses from our bundle adjustment

As explored in the prior works, the use of the inverse depth representation is known to be effective in regularizing the scales of the variables in the optimization. To utilize it in our case, we design a cost function (re-projection error) for the bundle adjustment to be computed on the unit sphere instead of in the image domain. This particularity is motivated by two major observations. Firstly, the spherical model takes into account the non-linear resolution induced by the fisheye lenses (the re-projection error is uniformly mapped on the sphere, which is not the case in the image domain). Secondly, the transformation from the unit sphere to the image coordinates yields strong non-linearity in the cost function which is not recommended for small motion bundle adjustment (hardly converges with a high-order model).

The j-th feature point lying on the sphere of the first camera is noted $\mathbf {\hat{X}}_{1j}$. Its corresponding 3D coordinates can be computed by back-projection using the inverse depth $(w_j \in \mathbf {W})$: $\mathbf {X}_j=\frac{\mathbf {\hat{X}}_{1j}}{w_j}$. Then, the projection of this 3D point onto the unit sphere of the i-th camera is calculated using the extrinsic camera matrix parameterized by a rotation vector $\mathbf {r}_i$ and a translation vector $\mathbf {t}_i$. This rigid transformation is followed by a normalization on the sphere: $\langle \mathbf {X} \rangle = \frac{\mathbf {X}}{\Vert \mathbf {X} \Vert }$.

By considering the frontal camera (F) and the rear camera (R) are fixed in a rigid body, our bundle adjustment is designed to refine the extrinsic parameters for the frontal camera images and the 3D coordinates of both features captured in the frontal and rear camera images by minimizing all the re-projection errors as:

(3)

where i and j stand for the image index and the feature index, $N_I$ the number of frames, $N_F$ and $N_R$ the numbers of features in the frontal and rear camera images, $\mathbf {\hat{X}}^F_{ij}$ and $\mathbf {\hat{X}}^R_{ij}$ the unit sphere coordinates of the j-th feature for the i-th image, and $\Vert \cdot \Vert _{\mathrm {H}}$ the Huber loss function with a scaling factor set as the focal length. The rigid motion matrices $\mathcal {P}^F_i$ and $\mathcal {P}^R_i$ are all expressed in a single referential coordinates system thanks to the $3\times 4$ extrinsic calibration matrix $\mathbf {P}$ (between the frontal camera to the rear camera):

(4)

where the function $\mathcal {R}$ transforms the Rodrigues rotation angles into their rotation matrix. For the initialization of the bundle adjustment parameters, all the rotation and translation vectors are set to zero which is a reasonable assumption for small motion 3D reconstruction [13–15]. The metric-scale extrinsic matrix $\mathbf {P}$ are pre-calibrated and our bundle adjustment takes advantage of the sensor parameters. This helps to estimate the rigid transformation between the frontal and the rear camera. Consequently, our BA is designed to embrace all inter-frame poses of both cameras in one optimization framework. Therefore, the reconstructed 3D structure and poses are estimated with an approximate metric scale (the scale may not be perfectly metric, but close to it). Thus, we can set the initial depth for all features as 10 m or 100 m for indoor or outdoor scene, respectively.

To find the feature correspondences for the frontal camera, we extract Harris corner features [30] from the first image. We filter out the features on the boundary pixels which has low image resolution and can cause inaccurate feature matching. By using a Kanade-Lucas-Tomashi (KLT) algorithm [31], these features are then tracked in the other images to find their correspondences, and tracked back to the first image to filter outliers by their bidirectional error. The points having an error larger than 0.1 pixel are discarded. The same process is done for the rear camera images. To solve the minimization problem, we use the Ceres solver [32] to optimize our bundle adjustment which uses Huber loss function to be robust to outliers.

3.3 Sphere Sweeping Algorithm

With the camera extrinsic parameters estimated from the previous section, our goal is to estimate dense depth maps for both fisheye images. The plane sweeping algorithm [18] is a powerful method for dense matching between multiview images. The main idea is to back-project the images onto successive virtual planes, perpendicular to the z-axis, and find the depth of the plane that has the highest photo consistency for each pixel. Hane et al. [12] adapt the plane sweeping algorithm to the fisheye camera model. Their idea is to adapt the planar homography on the unit sphere, which involves a systematic transformation between the sphere and the image plane.

Fig. 5.

Illustration on the sphere sweeping algorithm

Though the plane sweeping approach using fisheye camera can estimate a large field of view depth map, the accuracy can be lower especially for image boundary pixels due to their low spatial resolution [12]. A SPC can compensate this resolution issue by using the overlapping region between the rear and the frontal camera. To achieve this goal, we propose a new dense matching algorithm suitable for SPCs, called sphere sweeping (Fig. 5). Instead of using virtual planes, we utilize virtual spheres centered at the reference camera. It lets us utilize the color consistency of the overlapping region, which ensures a better estimation of the boundary depths.

Basically, our sphere sweeping algorithm back-projects the image pixel $\mathbf {u}$ in the reference image onto a virtual sphere $\mathbf {S}$, and then projects them onto the other images to obtain color intensity profiles $\mathcal {I}$. An important idea is that we can use two simultaneous virtual spheres centered at the frontal and rear cameras, respectively, and utilize them together for dense matching. When the l-th virtual spheres have an inverse radius (depth) $w_l$, the back-projections of $\mathbf {u}^{\!F}$ and $\mathbf {u}^{\!R}$ onto the frontal and rear camera’s virtual spheres are described respectively as:

$$\begin{aligned} \mathbf {S}^{\!F}_{l}=\hbar ^{-1}(\mathbf {K}_{\!F}^{-1}\mathbf {u}^{\!F},w_l),\, \mathbf {S}^{\!R}_{l}=\hbar ^{-1}(\mathbf {K}_{\!R}^{-1}\mathbf {u}^{\!R},w_l) \end{aligned}$$

(5)

Now, we can consider four possible cases of projections: frontal-to-frontal (FF), frontal-to-rear (FR), rear-to-frontal (RF), and rear-to-rear (RR). The projections of the frontal and rear camera’s spheres onto an i-th frontal camera image are computed by:

(6)

And the projections onto the i-th rear camera image are computed by:

(7)

Since each camera has a certain Field-Of-View (FOV), the projected image coordinates should be selectively used depending on whether they are in the field of view or not. For this reason, we measure the angle between the camera’s principal axis and the ray direction for each projection using the following formulations:

(8)

(9)

Fig. 6.

Examples of warped image and visibility ($i=1,\ l=0$). (a) Warped image from frontal to frontal. (b) Visibility mask of (a). (c) Warped image from rear to frontal image. (d) Visibility mask of (c).

Finally, the intensity profiles for the j-th pixel in the reference frontal and rear images w.r.t. the l-th inverse depth can be obtained by collecting the image intensities for all the corresponding visible projected points:

$$\begin{aligned} \mathcal {I}^{FF}_{lj}=\{ I^{F}_i(\mathbf {u}^{FF}_{lij}) | \theta ^{FF}_{lij}<\frac{\theta _{FOV}}{2} \}, \, \mathcal {I}^{FR}_{lj}=\{ I^{R}_i(\mathbf {u}^{FR}_{lij}) | \theta ^{FR}_{lij}<\frac{\theta _{FOV}}{2} \}, \end{aligned}$$

(10)

$$\begin{aligned} \mathcal {I}^{RF}_{lj}=\{ I^{F}_i(\mathbf {u}^{RF}_{lij}) | \theta ^{RF}_{lij}<\frac{\theta _{FOV}}{2} \}, \, \mathcal {I}^{RR}_{lj}=\{ I^{R}_i(\mathbf {u}^{RR}_{lij}) | \theta ^{RR}_{lij}<\frac{\theta _{FOV}}{2} \}. \end{aligned}$$

(11)

where $i=\{1,\cdots ,N_i\}$ and $\theta _{\!F\!O\!V}$ is the field-of-view angle ($200^{\circ }$ in our paper). A Bicubic interpolation is used for calculating the sub-pixel intensities. Figure 6 shows the examples of warped image and masks of reference image.

Table 1. Re-projection error percentage w.r.t. the number of iteration.

Our matching cost is formulated as a weighted sum of variances of two intensity profiles. The effectiveness of the variance as a matching cost for small motion case has been demonstrated in [15]. For the frontal and rear cameras, our matching costs are respectively:

$$\begin{aligned} V^{F}_{lj} = \mathrm {Var}(\mathcal {I}^{FF}_{lj}) + \lambda \mathrm {Var}(\mathcal {I}^{FR}_{lj}), \end{aligned}$$

(12)

$$\begin{aligned} V^{R}_{lj} = \mathrm {Var}(\mathcal {I}^{RR}_{lj}) + \lambda \mathrm {Var}(\mathcal {I}^{RF}_{lj}), \end{aligned}$$

(13)

where $\mathrm {Var}(\cdot )$ is the variance function and $\lambda$ is a weight for balancing the two variance values from the opposite side images. These costs are stacked over all the inverse depth candidates $w_1, \cdots , w_L$ to build cost volumes $\mathbf {V}^{\!F}$ and $\mathbf {V}^{\!R}$ for the frontal and rear camera, respectively.

Initial depth maps are extracted from $\mathbf {V}^{\!F}$ and $\mathbf {V}^{\!R}$ via Winner-Takes-All(WTA) method. For each of the frontal and rear camera’s cost volumes, we compute a confidence map as $\mathbf {C} = 1-\min (\mathbf {V})/\mathrm {median}(\mathbf {V})$ to remove outliers having confidence values under a certain threshold (<0.01). Finally, the depth maps are refined via a tree-based aggregation method proposed in [33]. It helps improving the quality of the results without masking out any depth on the un-textured region.

4 Experimental Results

We assess our method with both synthetic and real-world datasets. In Sect. 4.2, a large series of synthetic experiments is conducted with both to quantitatively measure the accuracy of our method with respect to the baseline magnitude and the number of images. A comparison of our method against the conventional plane sweeping with real images is provided in Sect. 4.3. These tests underline the high versatility of the proposed method with real-world data. We implemented our method using both MATLAB and C++. A computer equipped with an Intel i7 3.4 GHz and 16 GB was used for the computations. The proposed algorithm takes about 10 min for a 30 frames ($540\times 960$) sequence. Among all the computation steps, the dense matching is clearly the most time-consuming. But, it is expected that a GPU parallelization could significantly increase the speed of the overall algorithm [12, 34]. The algorithm for feature extraction, tracking and bundle adjustment takes about 1 min. The intrinsic and extrinsic parameters are pre-calibrated by using [35–37].

4.1 Validation for the Convergence and Scale Estimation

To demonstrate the effectiveness of the proposed BA in terms of convergence, we conduct multiple experiments against its conventional counter-part (BA on the image domain). Specifically, we measure the re-projection errors of both technique at every iteration. Table 1 shows re-projection error percentage (average over 20 datasets) with respect to the number of iteration. It is clear that the standard BA on the image domain does not converge at all, whereas, the proposed BA always converges well. It is because the double projection process (world to sphere and sphere to image) tends to generate singularities which induces many local minimum in the cost function.

As the proposed bundle adjustment is designed to approximately estimate the metric scale, we conduct a quantitative evaluation method to estimate the accuracy of the reconstructed scale obtained by our approach. To measure the scale, we use 3 types of calibration checkerboard (2, 5, 10 cm) with 3 different backgrounds and average the scale of the squares on the checkerboard. The reconstructed scale may not be perfectly metric scale since the baseline between two fisheye cameras is very small, but it is close to the metric as shown in Table 2, which could not be accomplished using previous pinhole-based SfSM methods [13–15]. We also measure the reconstructed scale values in Fig. 10(f), the height of the reconstructed bookshelf is 2 m, which in reality is 2.1 m.

Table 2. The average reconstructed scale value

4.2 Synthetic Datasets

For quantitative evaluation, we rendered synthetic image sequences for both frontal and rear camera (with ground-truth depth maps) via Blender™. The synthetic dataset consists of a pair of 30 images with a resolution of $480\times 960$ and a $200^{\circ }$ field of view. The two cameras are oriented at opposite directions in order to imitate the image sequences acquired from our spherical panoramic camera. We use the depth map robustness measure (R3) [14, 15, 38], which is the percentage of pixels that have less than 3 label differences from the depth map ground-truth¹ (see Fig. 8).

We performed experiments to evaluate the effect of the baseline magnitude and the number of images on the resulting depth maps. We firstly compute the R measures for baselines over the minimum depth value of the scene ($\text {Baseline}\,= \text {Min.depth} \times 10^{b}$) where $b=-3.5, -3.3,\ldots ,-1.1$. In Fig. 8(a), the R measure underlines that the proposed method achieves stable performances when the baseline b is larger than $-1.5$.

Next, Fig. 8(b) reports the performances of the proposed method according to the number of images used with a fixed baseline $b = -1.5$. We can observe that better performances are achieved with a greater number of images, however, the performance gain ratio is reduced as the number of images increases. The experiment shows that utilizing 20 images is a good trade-off between the performance gain and the burden of dense depth reconstruction for the proposed method. The example result and error map are shown in Fig. 7.

Fig. 7.

Our depth map and error map. (128 labels, $480\times 960$, FOV: 200)

Fig. 8.

Quantitative evaluation on the magnitude of baseline (left) and the number of images used (right).

Fig. 9.

Comparison on dense matching method.

Fig. 10.

The input images are captured by Ricoh Theta S video mode for one second (30 frames). (a)–(d) Outdoor scene. (e)–(f) Indoor scene. First row: Averaged image of video clip. Second row: Panorama images. Third row: Our depth map from small motion. Fourth row: Sparse 3D and Camera poses.

Fig. 11.

VR applications. Top: Averaged images of video clip, Middle: Anaglyph panoramic images(red-cyan), Bottom: Stereoscopic VR images.

4.3 Real-World Datasets

In this subsection, we demonstrate the performances of the proposed algorithm on various indoor and outdoor scenes captured by a Ricoh Theta S with video mode. For the real-world experiments, we use 1 second video clips for indoor scenes and uniformly sampled 30 images from 3 seconds video clips for outdoor datasets since the minimum depth in outdoor is usually larger than indoor scenes. The datasets were captured from various users with different motions.

To generate our panoramic images, we do not apply the standard approach which consists in the back-projection of both images on a common unit sphere. This approach is prone to parallax errors since the translation between the cameras is neglected. Instead, we project our dense 3D reconstruction on a unique sphere (located in between the two cameras) in order to create a synthetic spherical view which ensures a perfect stitching. This method preserves the structure of the scene by using all the intrinsic and extrinsic parameters (Fig. 10, 2nd row). Panorama depth maps are obtained by applying the similar process. As shown in Fig. 10 (4th row), the proposed method shows promising results regardless of the environment.

We also compare our sphere sweeping method with the conventional plane sweeping method using our hardware setup. The warped images via conventional homography-based method [12] are flipped on the boundary region where the FOV is larger than 180$^{\circ }$, so the depth maps estimated with these flipped images in Fig. 9(b) contain significant artifacts on the image boundary. Figure 9(c) and (d) show that the sphere sweeping method outperforms the competing method. Especially, the depth map (Fig. 9(d)) obtained with our strategy using overlapping regions shows better performance than that of single-side view.

4.4 Applications

Since our method can reconstruct accurate 3D of the surrounding environment, it can deliver a 360 degree 3D visual experience using a head-mounted display [1–3]. Many approaches propose to generate anaglyph panoramas [39] and stereoscopic images [40, 41], to produce VR contents in a cost effective way. In this subsection, we show the anaglyph panorama and the 360$^{\circ }$ stereoscopic images as applications.

In order to create a convincing 3D effect, we generate two synthetic views with the desired baseline (typically 5 to 7.5 cm to mimic the human binocular vision). The computation of such synthetic images is one again based on the dense 3D structure of the scene (as discussed in the previous section). The resulting anaglyphs and stereoscopic panoramas are available in Fig. 11. The 3D effect obtained with our method is realistic thanks to our accurate depth map computation approach.

5 Conclusion and Discussion

Discussion. In contrast to the prior SfSM BA methods [13–15] designed for pinhole cameras, our BA uses usual rotation representation, instead of the small-angle approximated matrix. Indeed, it has been demonstrated that spherical sensors are particularly robust to motion ambiguity while small magnitude motions are performed [42]. With this observation, the proposed BA may have the potential to be generalized to any type of motion. However, our method cannot handle large rotations due to the limitation of the feature tracking algorithm. This could be an interesting direction to pursue this work further.

Furthermore, we have noticed some degenerated cases throughout the course of the study. First, the estimated camera poses and the 3D points cannot be matched with the camera extrinsic parameters between frontal and rear cameras (metric scale) when the motion is only pure translation or only z-axis rotation. In this case, the estimated depth map on the fisheye cannot produce a well-aligned panorama depth. If the two cameras have zero baseline, the reconstruction is up to a scale factor, which may require an additional user input for adjusting the scale for stereoscopic rendering.

Conclusion. We have proposed a practical 3D reconstruction method for stereoscopic panorama from small motion with SPC. We achieved this by utilizing our bundle adjustment whose residuals are computed on unit sphere domain, and the estimated camera pose and 3D points are approximately metric. Our sphere sweeping algorithm enables to compute all-around dense depth maps, minimizing the loss of spatial resolution. With the estimated all-around image and depth map, we have shown practical utilities by introducing 360$^{\circ }$ stereoscopic and anaglyph images as VR contents.