Jensen Bregman LogDet Divergence Optimal Filtering in the Manifold of Positive Definite Matrices

Abstract

In this paper, we consider the problem of optimal estimation of a time-varying positive definite matrix from a collection of noisy measurements. We assume that this positive definite matrix evolves according to an unknown GARCH (generalized auto-regressive conditional heteroskedasticity) model whose parameters must be estimated from experimental data. The main difficulty here, compared against traditional parameter estimation methods, is that the estimation algorithm should take into account the fact that the matrix evolves on the PD manifold. As we show in the paper, measuring the estimation error using the Jensen Bregman LogDet divergence leads to computationally tractable (and in many cases convex) problems that can be efficiently solved using first order methods. Further, since it is known that this metric provides a good surrogate of the Riemannian manifold metric, the resulting algorithm respects the non-Euclidean geometry of the manifold. In the second part of the paper we show how to exploit this model in a maximum likelihood setup to obtain optimal estimates of the unknown matrix. In this case, the use of the JBLD metric allows for obtaining an alternative representation of Gaussian conjugate priors that results in closed form solutions for the maximum likelihood estimate. In turn, this leads to computationally efficient algorithms that take into account the non-Euclidean geometry. These results are illustrated with several examples using both synthetic and real data.

This work was supported in part by NSF grants IIS–1318145 and ECCS–1404163; AFOSR grant FA9550-15-1-0392; and the Alert DHS Center of Excellence under Award Number 2013-ST-061-ED0001.

1 Introduction

Covariance matrices are ubiquitous in computer vision, in problems ranging from tracking [7, 8, 16–18, 23, 29, 30, 32] to object detection [27, 28], person re-identification [11], activity recognition [15], face recognition [21] and Diffusion Tensor Imaging (DTI) [9, 22]. Applications outside the computer vision field include economics [3], fault detection [20] and power systems [6].

Fig. 1.

Two examples where covariance features are used to describe a target. On the left, the appearance of the target car has roughly constant covariance. On the right, the covariance of the appearance of the spinning ball changes over time.

Most of these applications require estimating the present value of a covariance matrix from a combination of noisy measurements and past historical data, with the main difficulty here arising from the need to account for the fact that these matrices evolve on a Riemannian manifold. For example, [23] proposed to use as covariance estimate the Karcher mean of the measurements, as a counterpart to the use of the arithmetic mean update in Euclidean space. However, this approach does not take into consideration measurement noise. Explicitly accounting for this noise leads to recursive filtering methods. In this context, [29] considered linear systems evolving on a Riemannian manifold and proposed a Kalman recursive scheme where a matrix $\log$ mapping (given a so called base point), is used to flatten the Positive Definite (PD) manifold prior to computing the predicted and corrected states. However, it is known that flattening the manifold often leads to less accurate distance calculation, resulting in poor prediction/estimation. Intrinsic extensions of recursive filtering where the on-manifold distance is considered were proposed in [7, 14]. A limitation of these approaches is that they assume that the present value of the covariance evolves according to a known first order model (that is, the present value of the covariance depends only on its most immediate past value). However, these assumptions do not necessarily hold in many practical scenarios where covariances evolve according to more complex dynamics that are not a-priori known (see Fig. 1).

To address these limitations, in this paper we propose a new framework for recursive filtering on the PD manifold using Generalized Autoregressive Conditional Heteroskedasticity (GARCH) models for propagating past measurements, combined with a maximum likelihood estimator based on minimizing the Jensen Bregman LogDet divergence. Specifically, we introduce a new probabilistic dynamic model for recursive filtering on the PD manifold based on a generalized Gaussian distribution. As shown in the paper, under suitable conditions, the generalized Gaussian conjugate prior can indeed be expressed in terms of the JBLD distance between the observed and predicted data. This key observation, combined with a data–driven GARCH model that propagates past values of the covariance, leads to a filter that admits a closed-form solution and compares favorably, both in terms of the estimation error and computational time, against existing approaches.

2 Preliminaries

2.1 Notation

2.2 Metrics in $\mathbb {S}_{++}^n$

The positive definite matrices form a convex cone in Euclidean space. However, it has been shown that metrics that do not take into account the geometry of the $\mathbb {S}_{++}^n$ manifold have poor accuracy in practical applications [1, 19]. As mentioned in [2], symmetric matrices with nonpositive eigenvalues are at finite distance from any PD matrix. Moreover, the Euclidean averaging of PD matrices often leads to a swelling effect, i.e. the determinant of the Euclidean mean can be strictly larger than the original determinants.

In order to take into account the non-flat manifold geometry of $\mathbb {S}_{++}^n$, an approximation to the geodesic distance can be obtained by using the matrix $\log$ operator to project PD matrices into a plane tangent to the Riemannian manifold. Then, the Frobenius norm of the difference between projections can be used as a surrogate for the geodesic distance, leading to the Log-Euclidean Riemannian Metric (LERM) [1]. However, as noted above, a potential pitfall of this approach is that flattening the PD manifold often leads to less accurate distance computation, which results in poor predictions. Alternatively, a full blown manifold metric such as the Affine Invariant Riemannian Metric (AIRM) [4, 22] can be utilized. This approach uses the geodesic length along the manifold curvature leading to the distance measure:

$$J_R(\mathbf {X},\mathbf {Y}) \doteq \Vert \log {\left( \mathbf {X}^{-\frac{1}{2}}\mathbf {Y}\mathbf {X}^{-\frac{1}{2}}\right) }\Vert _F$$

The main disadvantages of this metric are its high computational cost, and for the specific application in this paper, the lack of convexity¹. More recently, a family of metrics originating in the Jeffrey’s Kullback-Leibler divergence, which measure the distance between distributions, has been investigated. The main idea behind these metrics is to consider PD matrices as covariances of zero-mean Gaussian distributions. One of these metrics is the computationally efficient and empirically effective Jensen-Bregman LogDet Divergence [8]:

$$\begin{aligned} J_{ld}(\mathbf {X},\mathbf {Y}) \triangleq \log \left| \frac{\mathbf {X}+\mathbf {Y}}{2}\right| -\frac{1}{2}\log \left| \mathbf {X}\mathbf {Y}\right| \end{aligned}$$

(1)

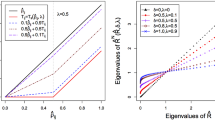
As noted in [13] the JBLD is geometry aware, has been proven to be non-flat [12, 26], and it is closely related to AIRM in how it measures geodesic length (see Theorem 1 in [13]). Furthermore, from the standpoint of this paper, the JBLD offers several advantages over the more traditional AIRM:

• 1. $J_{ld}(\mathbf {X},\mathbf {Y})^{\frac{1}{2}}$ is a metric [25].

• 2. If $0 \prec \underline{\sigma } \mathbf {I}\preceq \mathbf {X},\mathbf {Y} \preceq \overline{\sigma }\mathbf {I}$ then $J_{ld}(\mathbf {X},\mathbf {Y}) \le J_R^2(\mathbf {X},\mathbf {Y}) \le ( 2 \log {\frac{\overline{\sigma }}{\underline{\sigma }}})(J_{ld}(\mathbf {X},\mathbf {Y})+ n \log {2})$ [8].

• 3. For a fixed $\mathbf {Y}\in \mathbb {S}_{++}^n$, $J_{ld}(\mathbf {X},\mathbf {Y})$ is convex in the region $\{\mathbf {X}\in \mathbb {S}_{++}^n: \mathbf {X} \preceq (1+\sqrt{2})\mathbf {Y}\}$ [8].

Remark 1

The properties above, along with the empirically observed fact that $\sqrt{J_{ld}}$ is a good proxy for $J_R$ [25], motivate its use in this paper.

2.3 Inverse Wishart Distributions and GARCH Models

For the problems of interest in this paper, we need to model the evolution of a covariance matrix as a function of time. The models that we propose to use originate in the conjugate prior distribution of multivariate Gaussian sampling. Recall (see for instance [10]) that the likelihood function of the covariance matrix $\mathbf {P}$ of n independent observations $\mathbf {x}_i \sim \mathcal {N}(\mathbf {\varvec{\mu }},\mathbf {P})$ is given by the inverse Wishart distribution, that is:

$$\begin{aligned} L(\mathbf {P},\mathbf {Q}) \propto {|\mathbf {P}^{-1}|^{\frac{n-1}{2}} e^{-\frac{\mathrm{tr}(\mathbf {P}^{-1}\mathbf {Q})}{2}}} \end{aligned}$$

(2)

where $\mathbf {Q}$ denotes the empirical covariance, e.g. $\mathbf {Q} \doteq \sum _{i=1}^n (\mathbf {x}_i - \bar{\mathbf {x}}) (\mathbf {x}_i - \bar{\mathbf {x}})^T$ and $\bar{\mathbf {x}} \doteq \frac{\sum _{i=1}^n \mathbf {x}_i}{n}$.

Motivated by the models commonly used to propagate the parameters of Wishart distributions [3], we propose a GARCH model of the form:

$$\begin{aligned} p(\mathbf {P}_t|\mathbf {P}_{t-1},\dots ,\mathbf {P}_{t-r}) \propto e^{-\frac{J_{ld}(\mathbf {P}_t,\sum _{i=1}^r \mathbf {S}_{t-i}\mathbf {A}_i\mathbf {S}_{t-i})}{2\omega ^2}} \end{aligned}$$

(3)

where $\mathbf {S}_{t-i} \doteq \mathbf {P}_{t-i}^{\frac{1}{2}}$, r denotes the system order and where $\mathbf {A}_i \succ 0$ are the parameters that define the autoregressive model. Intuitively, the probability of obtaining a given covariance at time t decays exponentially with its distance, measured in the $J_{ld}$ sense, from the predictions of the model $\sum _{i=1}^r \mathbf {S}_{t-i}\mathbf {A}_i\mathbf {S}_{t-i}$. The effectiveness of this model in capturing the dynamics governing the evolution of matrices in $\mathbb {S}_{++}$ will be demonstrated in Sect. 5 with several examples.

Remark 2

Note that (3) can be indeed considered a generalization of multivariate stochastic volatility models, commonly used in econometrics to propagate covariances, to the case where the present value of the covariance depends on several past values. Specifically, under suitable conditions (see Theorem 1 in Sect. 4.1), $\mathbf {P}_t$ in (3) has an Inverse Wishart distribution with parameter $\mathbf {Q} \doteq \sum _{i=1}^r \mathbf {S}_{t-i}\mathbf {A}_i\mathbf {S}_{t-i}$, which in the case $r=1$ coincides with the WIC model proposed in [3].

Remark 3

The proposed model includes as a special case the simpler scalar model where $\mathbf {A}_i = a_i \mathbf {I}$. On the other hand, allowing the use of matrices allows modeling more complex sequences as illustrated by the next simple example. Consider a (periodic) covariance sequence,

$$\begin{bmatrix} 2&0 \\ 0&2 \end{bmatrix},\begin{bmatrix} 1&0 \\ 0&1 \end{bmatrix},\begin{bmatrix} 2&0 \\ 0&1 \end{bmatrix},\begin{bmatrix} 1&0 \\ 0&2 \end{bmatrix},\begin{bmatrix} 2&0 \\ 0&1 \end{bmatrix},\begin{bmatrix} 1&0 \\ 0&1 \end{bmatrix},\ldots $$

The corresponding GARCH model is given by:

$$P_t = S_{t-2}^T\begin{bmatrix} 1&0 \\ 0&0 \end{bmatrix}S_{t-2} + S_{t-3}^T\begin{bmatrix} 0&0 \\ 0&1 \end{bmatrix} S_{t-3}$$

which cannot be expressed as a scalar linear combination of $\mathbf {P}_{t-1}$, $\mathbf {P}_{t-2}$ and $\mathbf {P}_{t-3}$.

2.4 Problem Statement

In the context of the discussion in Sects. 2.2 and 2.3 the problem of interest in this paper can be stated as:

Problem 1

Given a noisy observation $\mathbf {Q}_t$ of a covariance matrix $\mathbf {P}_t$ and past historical data $\mathbf {P}_{t-r},\mathbf {P}_{t-r+1}, \cdots , \mathbf {P}_{t-1}$, find the JBLD-based maximum likelihood estimate (MLE) of $\mathbf {P}_t$.

We propose to solve this problem by splitting it into two subproblems, (i) estimating the propagation model parameters from training data and (ii) finding a maximum likelihood estimate of $\mathbf {P}_t$ assuming that the propagation model is known. Formally, this leads to the following two problems:

Problem 2

Given a sequence of training data $\{\mathbf {P}_t\}_{t=1}^T\in {\mathbb S}_{++}^n$, find the JBLD-based maximum a posteriori estimate (MAP) of the parameters $\mathbf {A}_i$, such that the dynamic model is stable.

Problem 3

Given a noisy observation $\mathbf {Q}_t$, find the JBLD-based maximum likelihood estimate of $\mathbf {P}_t$, assuming a known propagation model of the form (3).

3 Estimation of the GARCH Model

Since the right hand side of (3) does not define a positive definite kernel for all $\omega$ (or equivalent, the JBLD cannot be isometrically embedded in a Hilbert space unless restricted only to commuting matrices [26]), it follows that the problem of estimating the propagation model for $\mathbf {P}_t$ cannot be solved by mapping the data to a Hilbert space and using classical, Euclidean geometry based techniques there. Nevertheless, as we show in this section, Problem 2 can be reduced to a convex optimization and efficiently solved by exploiting the properties of the JBLD.

Given a sequence of training data $\{\mathbf {P}_t\}_{t=1}^T$, estimating the model parameters in (3) is equivalent to solving the following MAP problem:

(4)

where the second constraint enforces that the prediction should be not too far from the training data, and where the last constraint has been added to enforce stability of the resulting model. Using (3) this problem reduces to:

(5)

Since $J_{ld}(\mathbf {X},\mathbf {Y})$ is convex with respect to $\mathbf {X}$ in the region $\mathbf {X} \preceq (1+\sqrt{2})\mathbf {Y}$ [8] it follows that, as long as the problem is feasible, then it is convex and can be solved using for instance a first order, ADMM type method. Further, by using a splitting-variable type argument, it can be shown that in this case all intermediate steps in the ADMM method admit a closed-form solution [31]. Combining this observation with the adaptive method for adjusting the penalty parameter $\mu$ in the corresponding augmented Lagrangian and the stopping criteria proposed in [5], leads to a computationally very efficient algorithm for solving (5).

4 A JBLD Maximum Likelihood Estimator

In this section, we show that a suitably modified version of Problem 3 admits a closed form solution. To this effect, we begin by re-examining the conjugate prior of the multivariate Gaussian distribution.

4.1 A Generalized Gaussian Conjugate Prior

Combining (2) and (3) it follows that the MLE of $\mathbf {P}_t$, the present value of the covariance given an observation $\mathbf {Q}_t$ and past values $\mathbf {P}_{t-r}^{t-1}$ satisfies:

$$\begin{aligned} \begin{aligned} L(\mathbf {P},\mathbf {Q},\mathbf {P}_{t-r}^{t-1}) \propto&{|\mathbf {P}^{-1}|^{\frac{n-1}{2}} e^{-\frac{\mathrm{tr}(\mathbf {P}^{-1}\mathbf {Q})}{2}}} \times \\ {}&e^{-\frac{J_{ld}(\mathbf {P}_t,\sum _{i=1}^r \mathbf {S}_{t-i}\mathbf {A}_i\mathbf {S}_{t-i})}{2\omega ^2}} \end{aligned} \end{aligned}$$

(6)

In principle, this expression can be used to find a MLE of $\mathbf {P}_t$. However, the resulting optimization problem is not amenable to closed form solutions. In addition, the first factor in (6) does not take into account the manifold geometry. As we show next, surprisingly, if $\Vert \mathbf {Q}\mathbf {P^{-1}} - \mathbf {I}\Vert$ is small, that is the prediction and observation are roughly aligned, then (6) can be expressed in terms of the JBLD, leading to closed form solutions.

Theorem 1

Let $\mathbf {X} \doteq \mathbf {P}^{-\frac{1}{2}}\mathbf {Q}\mathbf {P}^{-\frac{1}{2}}$ and denote by $\lambda _i$ the eigenvalues of $\varvec{\varDelta } \doteq \frac{\mathbf {X}-\mathbf {I}}{2}$. Then,

$$\begin{aligned} e^{-\frac{1}{2\sigma ^2}J_{ld}(\mathbf {P},\mathbf {Q})} \,{\propto } \, |\mathbf {P}^{-1}|^{\frac{n-1}{2}} e^{-\frac{\mathrm{tr}(\mathbf {P}^{-1}\hat{\mathbf {Q}})}{2}} + \mathcal {O}(\lambda _i) \end{aligned}$$

(7)

where, for notational simplicity we defined $\frac{1}{2\sigma ^2} \doteq n$ and $\hat{\mathbf {Q}} \doteq n\mathbf {Q}$.

Proof

From the explicit expression of $J_{ld}$ it follows that

$$\begin{aligned} \begin{aligned} e^{-\frac{1}{2\sigma ^2}J_{ld}(\mathbf {P},\mathbf {Q})}&= |\mathbf {X}|^{\frac{1}{4\sigma ^2}}\left| \mathbf {I}+\frac{\mathbf {X}-\mathbf {I}}{2}\right| ^{-\frac{1}{2\sigma ^2}} = |\mathbf {X}|^{\frac{1}{4\sigma ^2}} \prod _{i=1}^d (1+\lambda _i) ^{-n} \end{aligned} \end{aligned}$$

(8)

Next, note that

$$\begin{aligned} \begin{aligned} \prod _{i=1}^d (1+\lambda _i)^{-n}&={\,}(1-n\sum _{i=1}^d \lambda _i + \mathcal {O}(\lambda _i^2)) =e^{-n\sum _{i=1}^d \lambda _i} + \mathcal {O}(\lambda _i^2) \\&={\,}e^\frac{-n \cdot \text {tr}(\mathbf {X}-\mathbf {I})}{2} + \mathcal {O}(\lambda _i^2) = e^\frac{-n\cdot \text {tr}(\mathbf {X})}{2} e^{\frac{nd}{2}}+ \mathcal {O}(\lambda _i^2) \end{aligned} \end{aligned}$$

(9)

Replacing (9) in (8) and using the fact that

$$\begin{aligned} \begin{aligned} |\mathbf {X}|^{\frac{n}{2}}&= |\mathbf {X}|^{\frac{n-1}{2}}|\mathbf {X}|^{\frac{1}{2}} = |\mathbf {X}|^{\frac{n-1}{2}}|\mathbf {I}+\varvec{\varDelta } + \mathcal {O}(\lambda _i^2)| = |\mathbf {X}|^{\frac{n-1}{2}}(1 + \mathcal {O}(\lambda _i)) \end{aligned} \end{aligned}$$

(10)

yields:

$$\begin{aligned} \begin{aligned} e^{-\frac{1}{2\sigma ^2}J_{ld}(\mathbf {P},\mathbf {Q})}&= e^{\frac{d}{4\sigma ^2}}|\mathbf {X}|^{\frac{n-1}{2}}e^{-\frac{\text {tr}(\mathbf {P}^{-1}\mathbf {nQ})}{2}} +\mathcal {O}(\lambda _i) \\&\propto |\mathbf {P}^{-1}|^{\frac{n-1}{2}}e^{-\frac{\text {tr}(\mathbf {P}^{-1}\mathbf {\hat{Q}})}{2}} +\mathcal {O}(\lambda _i) \end{aligned} \end{aligned}$$

(11)

Remark 4

The result above shows that, to the first order, the likelihood function of a Wishart distribution can be approximated by a kernel using the JBLD. To the best of our knowledge,this is the first result establishing this connection, which is the key to obtaining a fast MLE given in terms of the Stein mean.

4.2 An Explicit MLE

From Theorem 1 and (3) it follows that Problem 3 can be solved using a likelihood function of the form:

$$\begin{aligned} \begin{aligned} p(\mathbf {P}_t|\mathbf {Q}_t,\mathbf {P}_{t-1},\dots , \mathbf {P}_{t-r}) =&\frac{1}{Z_s} e^{-\frac{J_{ld}(\mathbf {Q}_t,\mathbf {P}_t)}{2\phi ^2}} \\ \times&e^{-\frac{J_{ld}(\mathbf {P}_t,\sum _{i=1}^r \mathbf {S}_{t-i}\mathbf {A}_i\mathbf {S}_{t-i})}{2\omega ^2}} \end{aligned} \end{aligned}$$

(12)

where $\mathbf {Q}_t$ denotes the noisy observation and $Z_s$ is a normalization factor. In this context, the MLE of $\mathbf {P}_t$ is given by:

$$\begin{aligned} \mathbf {P}_{t}^* = \arg \max _{\mathbf {P}_t} p(\mathbf {P}_t|\mathbf {P}_{t-1},\dots ,\mathbf {P}_{t-r})p(\mathbf {P}_t|\mathbf {Q}_t) \end{aligned}$$

(13)

or, equivalently,

$$\begin{aligned} {\begin{aligned} \mathbf {P}_t^* =&\arg \min _{\mathbf {P}_t} (1-\lambda ) J_{ld}(\mathbf {P}_t,\sum _i\mathbf {S}_{t-i}\mathbf {A}_i\mathbf {S}_{t-i}) \\&+ \, \lambda J_{ld}(\mathbf {P}_t,\mathbf {Q}_t) \end{aligned}} \end{aligned}$$

(14)

where, $\lambda =\frac{\omega ^2}{\omega ^2+\phi ^2}$. The solution to this optimization is a weighted Stein Mean, which admits the following closed form solution [24]:

$$\begin{aligned} \begin{aligned} \mathbf {P}_t^*=&\tilde{\mathbf {P}}_t\left[ \sqrt{\tilde{\mathbf {P}}_t^{-1}\mathbf {Q}_t+\frac{(2\lambda -1)^2}{4}(\mathbf {I}-\tilde{\mathbf {P}}_t^{-1}\mathbf {Q}_t)^2}\right. \\&\left. -\frac{2\lambda -1}{2}(\mathbf {I}-\tilde{\mathbf {P}}_t^{-1}\mathbf {Q}_t)\right] \end{aligned} \end{aligned}$$

(15)

where $\tilde{\mathbf {P}}_t=\sum _{i=1}^r \mathbf {S}_{t-i}\mathbf {A}_i\mathbf {S}_{t-i}$, leading to the JBLD recursive filter algorithm outlined in Algorithm 1.

5 Experiments

In this section, we illustrate the advantages of the proposed JBLD recursive filter (JBRF) by comparing its performance using both synthetic data and real data, against the following three state-of-the-art methods:

Manifold Mean. [23] proposed using the Karcher mean of past observations as the estimator for the present value of the covariance. Note that the Karcher mean is based on using the Affine Invariant Riemannian metric. Thus, for consistency, we modified this method to use the Stein, rather than the Karcher, mean, since the former is the manifold mean under the JBLD metric used in this paper. In the experiments involving synthetic and video clips downloaded from Youtube, we set the memory length of this method to 20, which allows it to use a larger number of past observations compared to JBRF, IRF and LRF.

LRF. The recursive filter for linear system on PD manifold introduced in [29] obtained using the Euclidean distance computed using the matrix $\log$ and $\exp$ operator to flatten the manifold.

IRF. The intrinsic recursive filter on PD manifold proposed in [7].

Fig. 2.

Mean estimation error from 20 trials for the synthetic data experiment.

5.1 Synthetic Data Experiments

The goal here is to compare all methods in a simple scenario: estimation of a constant covariance matrix in $\mathbb {S}_{++}^3$. Thus, a time sequence of corrupted observations was randomly sampled by adding Gaussian noise to an identity matrix $\mathbf {I}_3$. First, a vector $\mathbf {w}\in \mathbb {R}^6$ was sampled from a Gaussian distribution ${\mathcal N}(0,\sigma ^2\mathbf {I}_6)$, and used to form a matrix $\mathbf {W}\in \mathbb {S}^3$. Then the noise $\mathbf {W}$ was added to $\mathbf {I}_3$ using the manifold exponential operator $\exp _{\mathbf {X}}(\mathbf {v})$

$$\begin{aligned} \exp _{\mathbf {X}}(\mathbf {v}) = \mathbf {X}^{1/2}\exp _m(\mathbf {X}^{-1/2}\mathbf {v}\mathbf {X}^{-1/2})\mathbf {X}^{1/2} \end{aligned}$$

(16)

Note that the manifold exponential operator maps the tangent vector $\mathbf {v}$ to the location on the manifold reached in a unit time by the geodesic starting at $\mathbf {X}$ in the tangent direction.

We chose $\sigma ^2=\{0.1,1,2\}$, and for each value we generated 20 sequences of length 1000, which can be viewed as random measurements of the identity matrix. Our recursive filter was applied as an estimator of the sequence, as well as the Manifold Mean method, IRF and LRF. The estimation error was computed using the JBLD between the estimations and the ground truth $\mathbf {I}_3$. For each value of $\sigma ^2$, we took the mean of the estimation error over the corresponding 20 sequences.

The value of the tuning parameters for IRF and LRF was chosen according to the corresponding set-ups. For IRF, the parameters were set to $\phi ^2/\omega ^2=200$, as reported in [7]. For LRF, we set $\varvec{\varOmega }=\omega \mathbf {I}_6$ with $\omega =0.0001$ and $\varvec{\varPhi }=\sigma ^2\mathbf {I}_6$ as reported in [29]. For the base point of LRF, we used the first observation of each sequence, which is the best information available about the sequence before filtering. The justification for this setting is given in [7]. For our filter, we set the parameters as $\phi ^2/\omega ^2=50$.

The mean estimation errors from 20 trials for each different noise level are shown in Fig. 2a, b and c. It can be observed that both Manifold Mean and LRF converge faster than JBRF in terms of the number of iterations. However, as the noise level increases, the estimation error of LRF gets larger, which leads to the worst performance compared to JBRF and IRF. On the other hand, the performance of Manifold Mean is constant, and worse than JBRF and IRF but better than LRF for larger noise level. The reason of this poor performance of Manifold Mean on synthetic data is that a memory length of 20 is still not enough to eliminate the noise effects. However, even for a memory length of 20, the Stein Mean computation is already the slowest in terms of computing time. Both IRF and our method show robust performance with respect to different noise levels. In terms of running time, the proposed method is the fastest, with an average time of 0.11 s for each sequence, running on a iMAC with a 4 GHz CPU. This is about 6 times faster than LRF (0.66 s), around 20 times faster than IRF (2.43 s) and almost two orders of magnitude faster than calculating the Stein mean (on average 10 s).

Fig. 3.

Tracking under occlusion. Top: sample training data. Bottom: tracking results using different filters.

5.2 Tracking Under Occlusion and Clutter

This lab experiment was specifically designed to provide a very challenging environment, shown in Fig. 3. The goal here is to track a multicolored spinning ball in the presence of occlusion (frames $16{-}19$) and clutter whose color covariance descriptors are, in some frames, similar to those of the target. Note that, due to the spinning, the appearances of the target as it enters and emerges from the occlusion are different, thus necessitating a data-driven framework capable of accurately predicting this change. We first used the information from frames 1 to 14 to identify an $11^\mathrm{{th}}$ order model of the form (3) that captures the evolution of the covariance feature obtained from the coordinates and color of the target:

$$\begin{aligned} f(x,y) = \begin{bmatrix} x&y&R(x,y)&G(x,y)&B(x,y) \end{bmatrix} \end{aligned}$$

(17)

Next, we used the different filters to estimate the covariance feature starting from frame 15, which is the last unoccluded frame, based on the data from frames $1{-}14$. To this effect, we first used the dynamical model to predict the covariance feature in the next frame. Next, we searched for the best match (in the JBLD or, in the case of IRF, AIRM, sense) by comparing against the covariance features obtained using a sliding window. Changing target size was handled by dense scanning (using the integral image trick) with target sizes ranging between 85 % and 115 %, in increments of 5 %, of the last size. The best match was chosen as the target in the frame and used as observation to perform the correction step in all filtering methods. During the occlusion, no correction step was performed. Again, for LRF and IRF, the parameters were chosen as reported in [29] and [7]. For this experiment, we also compared against the method proposed in [14] (MUKF), using the code provided by the authors, where the target bounding box was modified to be rectangular as in the other methods. For JBRF, we set $\omega = 0.01$, and $\phi =0.01$.

As shown in Fig. 3, only the proposed method is capable of sustained tracking. This is due to the fact that the LRF, IRF, and MUKF methods cannot accurately predict the evolution of the covariance because they use at most information of the previous two frames and thus cannot handle long occlusions. Finally, the Stein Mean method, even using information from more than the past 11 frames, fails due to the fact that the updating methodology does not reflect the dynamic evolution of the target.

5.3 Youtube Video Experiments

In this experiment, we evaluate the proposed filter using several Youtube videos with more than 1000 frames in total. The videos contain a spinning multicolored ball and fish schooling behavior. We divided each sequence into two parts: training data (around $60\,\%$) and testing data (around $40\,\%$). For each sequence, we first extracted RGB covariance features from the object (the spinning ball or the entire fish school) and used the training data to estimate the model parameters for JBRF. The system order was determined empirically, by searching for the best fit. The data was corrupted with Gaussian noise ${\mathcal N}(0,0.01)$ prior to extracting the covariance features. These corrupted covariance sequences were then processed using the different estimation methods. The tuning parameters for this experiment were set as follows. For JBRF and IRF, we first calculated the fitting error of the state transition, in the corresponding non-Euclidean metric, using the training sequence and associated system model. The parameter $\omega$ for JBRF and IRF was then set to the unbiased estimation of the standard deviation using these fitting errors. For the parameter $\phi$ which controls the variance of the observation noise, we performed a grid search with values $1e\{-3,-2,-1,0,1,2,3\}$ and used the one giving minimum estimation error. For LRF, we set $\omega =0.0001$ as proposed in [29], and performed a grid search for $\phi$ with values $1e\{-3,-2,-1,0,1,2,3\}$. The results reported correspond to the value that yielded the minimum estimation error.

Table 1. Mean estimation error and running time for the experiments using Youtube video clips (number in parenthesis denotes the system order of JBRF model)

The estimation error was again computed using JBLD between the estimations and the ground truth (extracted from frames before corruption). The mean estimation errors and average run time to filter 100 frames are shown in the Table 1. Sample frames from several sequences are shown in Fig. 4 along with their noise corrupted counterparts. Table 1 shows that indeed JBRF achieves the minimum estimation error among all methods, while, at the same time being 60 % faster than the closest competitor. It is also worth emphasizing that the performance improvement is not just due to the fact that the JBLR can use higher order models. As shown in the last five columns of the table, using a data driven model leads to substantial performance improvement, even when the order of this model is comparable to the one used by competing methods.

Fig. 4.

Sample frames from Youtube videos. Top: original sequences. Bottom: sequences corrupted by noise.

6 Conclusion

Many computer vision applications require estimating the value of a positive definite matrix from a combination of noisy measurements and past historical data. In this paper, we proposed a framework for obtaining maximum likelihood estimates of both the dynamic propagation model and of the present value of the matrix. The main advantages of the proposed approach, compared against existing techniques are (i) the ability to identify the propagation model and to exploit it to obtain better predictions while taking into account the non-Euclidean geometry² of the problem, and (ii) the use of a generalized Gaussian approximation to the Jensen-Bregman LogDet Divergence that leads to closed form maximum likelihood estimates. As illustrated both with synthetic and video data, the use of the identified manifold dynamics combined with the JBLD metric leads to filters that compare favorably against existing techniques both in terms of the estimation error and the computational time required to compute the estimates.