Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Since the introduction of support vector machines (SVMs) [1, 2] various variants have been developed to improve the generalization ability. Because SVMs do not assume a specific data distribution, a priori knowledge on the data distribution can improve the generalization ability. The Mahalanobis distance, instead of the Euclidean distance is useful for this purpose. One approach reformulates SVMs so that the margin is measured by the Mahalanobis distance [3–7], and another approach uses Mahalanobis kernels, which calculate the kernel value according to the Mahalanobis distance [8–13].

In SVMs, the minimum margin is maximized. But in AdaBoost [14], the margin distribution, instead of the minimum margin, has been known to be important in improving the generalization ability [15, 16].

Several approaches have been proposed to control the margin distribution in SVM-like classifiers [17–22]. In [18], a maximum average margin classifier (MAMC) is proposed, in which instead of maximizing the minimum margin, the margin mean for the training data is maximized without slack variables. In [21, 22], in addition to maximizing the margin mean, the margin variance is minimized and the classifier is called large margin distribution machine (LDM). According to the computer experiments in [21], the generalization ability of MAMCs is inferior to SVMs and LDMs.

In this paper, we clarify why MAMCs perform poorly for some classification problems and propose two methods to improve the generalization ability. Because the MAMC does not include constraints associated with training data, the determined bias term depends only on the difference between the numbers of training data for the two classes. To solve this problem, after the weight vector is obtained by the MAMC, we optimize the bias term so that the classification error is minimized. Then to improve the generalization ability further, we introduce a weight parameter to the average vector of one class and determine the parameter value by cross-validation. This results in optimizing the slope of the separating hyperplane. To improve the generalization ability further, we define the equality-constrained MAMC (EMAMC), which is shown to be equivalent to the least squares (LS) SVM. Using two-class problems, we show that the generalization ability of the unconstrained MAMCs with the optimized bias term and slopes are inferior to that of the EMAMC.

In Sect. 2, we explain the architecture of the MAMC and clarify the problems of MAMC. Then, we propose bias term optimization and slope optimization and develop the EMAMC. In Sect. 3, we compare the generalization abilities of the MAMC with those of the proposed MAMC with optimized bias terms and slopes, the EMAMC, and the SVM.

2 Maximum Average Margin Classifiers

2.1 Architecture

In the following we explain the maximum average margin classifiers (MAMCs) according to [18].

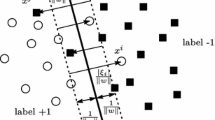
We consider a classification problem with M training input-output pairs \(\{\mathbf{x}_i, y_i\}\) (\(i = 1, \ldots , M\)), where \(\mathbf{x}_i\) are m-dimensional training inputs and belong to Class 1 or 2 and the associated labels are \(y_i = 1\) for Class 1 and \(-1\) for Class 2. We map the m-dimensional input vector \(\mathbf{x}\) into the l-dimensional feature space using the nonlinear vector function \(\varvec{\phi }(\mathbf{x})\). In the feature space, we determine the decision function that separates Class 1 data from Class 2 data:

$$\begin{aligned} f(\mathbf{x})= \mathbf{w}^{\top } \varvec{\phi }(\mathbf{x}) + b=0, \end{aligned}$$
(1)

where \(\mathbf{w}\) is the l-dimensional vector, \({\top }\) denotes the transpose of a vector (matrix), and b is the bias term.

The margin of \(\mathbf{x}_i\), \(\delta _i\), which is the distance from the hyperplane, is given by

$$\begin{aligned} \delta _i = y_i \,(\mathbf{w}^{\top } \varvec{\phi }(\mathbf{x}_i) + b)/\Vert \mathbf{w}\Vert . \end{aligned}$$
(2)

Under the assumption of

$$\begin{aligned} \mathbf{w}^{\top } \, \mathbf{w}=1, \end{aligned}$$
(3)

(2) becomes

$$\begin{aligned} \delta _i = y_i \,(\mathbf{w}^{\top } \varvec{\phi }(\mathbf{x}_i) + b). \end{aligned}$$
(4)

With \(b=0\), the MAMC, which maximizes the average margin, is defined by

$$\begin{aligned} \text {maximize}\quad Q(\mathbf{w})=\frac{1}{M}\sum _{i=1}^{M} y_i \,\mathbf{w}^{\top } \varvec{\phi }(\mathbf{x}_i) \end{aligned}$$
(5)
$$\begin{aligned} \text {subject to}\quad \mathbf{w}^{\top } \, \mathbf{w} = 1. \end{aligned}$$
(6)

Introducing the Lagrange multiplier \(\lambda \, (>0)\), we obtain the unconstrained optimization problem:

$$\begin{aligned} \text{ maximize }\quad Q(\mathbf{w})=\frac{1}{M}\sum _{i=1}^{M} y_i \,\mathbf{w}^{\top } \varvec{\phi }(\mathbf{x}_i)-\frac{\lambda }{2}( \mathbf{w}^{\top } \, \mathbf{w} - 1). \end{aligned}$$
(7)

Taking the derivative of Q with respect to \(\mathbf{w}\), we obtain the optimal \(\mathbf{w}\):

$$\begin{aligned} {\lambda }\, \mathbf{w}=\frac{1}{M}\sum _{i=1}^{M} y_i \,\varvec{\phi }(\mathbf{x}_i). \end{aligned}$$
(8)

In [18], \(\lambda \) is determined using (6) and (8), but \(\lambda \) can take on any positive value because that does not change the decision boundary. Therefore, in the following we set \(\lambda =1\).

In calculating the decision function given by (1), we use kernels \(K(\mathbf{x}, \mathbf{x}') = \varvec{\phi }^{\top }(\mathbf{x}) \, \varvec{\phi }(\mathbf{x})\) to avoid treating the variables in the feature space explicitly.

The resulting decision function \(f(\mathbf{x})\) with \(b=0\) is given by

$$\begin{aligned} f(\mathbf{x}) = \frac{1}{M}\sum _{i=1}^M y_i \, K(\mathbf{x}, \mathbf{x}_i). \end{aligned}$$
(9)

Among several kernels, radial basis function (RBF) kernels are widely used and thus in the following study we use RBF kernels:

$$\begin{aligned} K(\mathbf{x},\mathbf{x}') = \exp (-\gamma ||\mathbf{x}-\mathbf{x}'||^{2}/m), \end{aligned}$$
(10)

where m is the number of inputs for normalization and \(\gamma \) is to control a spread of a radius.

2.2 Problems with MAMCs

The MAMC is derived without a bias term, i.e., \(b=0\). To include the bias term we change (7) to

$$\begin{aligned} \text{ maximize }\quad Q(\mathbf{w}, b)=\frac{1}{M}\sum _{i=1}^{M} y_i \,(\mathbf{w}^{\top } \varvec{\phi }(\mathbf{x}_i)+b)-\frac{1}{2}( \mathbf{w}^{\top } \, \mathbf{w} +b^2). \end{aligned}$$
(11)

Here, we replace \(\lambda \) with 1 and delete the constant term. Then, Q is maximized when

$$\begin{aligned} \mathbf{w}=\frac{1}{M}\sum _{i=1}^{M} y_i \,\varvec{\phi }(\mathbf{x}_i), \end{aligned}$$
(12)
$$\begin{aligned} {b}=\frac{1}{M}\sum _{i=1}^{M} y_i. \end{aligned}$$
(13)

From (13), b is determined by the deference of the numbers of the data belonging to Classes 1 and 2, not by the distributions of the data belonging to the two classes. And if the numbers are the same, \(b=0\), irrespective of \(\mathbf{x}_i \, (i=1,\ldots ,M)\). This occurs because the coefficient of b becomes zero in (11); the value of b does not affect optimality of the solution.

This means that the constraints are lacking for determining the optimal value of b. Similar to SVMs, the addition of inequality or equality constraints for the training data may solve the problem, which will be discussed later.

2.3 Bias Term Optimization

In this section we propose two-stage training; in the first stage, we determine the coefficient vector \(\mathbf{w}\) by (12), and in the second stage, we optimize the value of b by

$$\begin{aligned} \text {minimize}\quad E_{\mathrm R}=\sum _{i=1}^M I(\xi _i) \end{aligned}$$
(14)
$$\begin{aligned} {\text {subject to}}\quad&y_{i} {} ({\mathbf {w}}^{{ \top }} \varvec{\phi } ({\mathbf {x}}_{i} ) + b) \ge \rho - \xi _{i} \nonumber \\&\rho > 0,\quad \xi _{i} \ge 0, \end{aligned}$$
(15)

where \(E_{\mathrm R}\) is the number of misclassifications, \(\rho \) is a positive constant, \(\xi _i \, (\ge 0)\) is a slack variable, \(I(\xi _i) = 0\) for \(\xi _i=0\) and \(I(\xi _i) = 1\) for \(\xi _i>0\). If there are multiple b values that minimize (14), we break the tie by

$$\begin{aligned} \text{ minimize }\quad&E_{\mathrm S} = \displaystyle \sum _{i=1}^M \xi _i, \end{aligned}$$
(16)

where \(E_{\mathrm S}\) is the sum of slack variables.

First we consider the case where the classification problem is separable in the feature space. Suppose that

$$\begin{aligned} \max _{j=1,\ldots ,M\atop y_j =-1}{} \mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_j)< \min _{i=1,\ldots ,M\atop y_i=1}{} \mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_i) <0 \end{aligned}$$
(17)

is satisfied, where training data belonging to Class 2 are correctly classified but some of the training data belonging to Class 1 are misclassified. Because of the first inequality in (17), by setting a proper value to b, all the training data are correctly classified.

Let

$$\begin{aligned} j= {\displaystyle \arg _j} \max _{j=1,\ldots ,M\atop y_j =-1}{} \mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_j), \quad i=\arg _i \min _{i=1,\ldots ,M\atop y_i=1}{} \mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_i). \end{aligned}$$
(18)

Then, from (15), to make \(\mathbf{x}_i\) and \(\mathbf{x}_j\) be correctly classified with margin \(\rho \),

$$\begin{aligned} \mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_i) + b = \rho , \quad -(\mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_j) + b) = \rho \end{aligned}$$
(19)

must be satisfied. Thus,

$$\begin{aligned} b= -\frac{1}{2}(\mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_i)+\mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_j)),\quad \rho =\frac{1}{2}(\mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_i)-\mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_j)). \end{aligned}$$
(20)

The above equations are also valid when

$$\begin{aligned} 0<\max _{j=1,\ldots ,M\atop y_j =-1}{} \mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_j) < \min _{i=1,\ldots ,M\atop y_i=1}{} \mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_i), \end{aligned}$$
(21)

where some of the training data for Class 2 are misclassified.

It is clear that (20) satisfies \(E_{\mathrm R} = E_{\mathrm S} =0\) and that \(\rho \) is the maximum.

Now consider the inseparable case. Let the misclassified training data for Class 1 be \(\mathbf{x}_{i_k} \, (k=1,\ldots ,p)\) and

$$\begin{aligned} \mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_{i_1}) \le \mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_{i_2}) \le \cdots \le \mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_{i_p})\le 0. \end{aligned}$$
(22)

Likewise, let the misclassified training data for Class 2 be \(\mathbf{x}_{j_k} \, (k=1,\ldots ,n)\) and

$$\begin{aligned} 0 \le \mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_{j_1}) \le \mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_{j_2}) \le \cdots \le \mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_{j_n}). \end{aligned}$$
(23)

Similar to the separable case, it is clear that the optimal b occurs at (20) with \(i=i_k \,(k\in \{1,\ldots ,p\})\) and j being given by

$$\begin{aligned} j=\arg _j \, \max _{\mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_{j}) <\mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_{i_k})\atop y_j= -1, j=1,\ldots ,M} \mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_{j}) \end{aligned}$$
(24)

or with \(j=j_k \,(k \in \{1,\ldots ,n\})\) and i being given by

$$\begin{aligned} i=\arg _i \, \max _{\mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_{j_k}) <\mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_{i})\atop y_i = 1, i=1,\ldots ,M} \mathbf{w}^{\top }\,\varvec{\phi }(\mathbf{x}_{i}). \end{aligned}$$
(25)

Let \(E_{\mathrm R}(i,j)\) and \(E_{\mathrm S}(i,j)\) denote that \(E_{\mathrm R}\) and \(E_{\mathrm S}\) are evaluated with b determined using \(\mathbf{x}_i\) and \(\mathbf{x}_j\) by (20), where \(i=i_k \,(k\in \{1,\ldots ,p\})\) and j is given by (24) or \(j=j_k \, (k \in \{1,\ldots ,n\})\) and i is given by (25). For each pair of i and j, we calculate \(E_{\mathrm R}(i,j)\) and select the value of b that minimizes \(E_{\mathrm R}(i,j)\). If there are multiple pairs of i and j, we select the value of b that minimizes \(E_{\mathrm S}(i,j)\).

2.4 Extension of MAMCs

Characteristics of Solutions. Rewriting (8) with \(\lambda = 1\),

$$\begin{aligned} \mathbf{w}= & {} \frac{M_+}{M}\bar{\varvec{\phi }}_+-\frac{M_-}{M}\bar{\varvec{\phi }}_- \end{aligned}$$
(26)

where

$$\begin{aligned} \bar{\varvec{\phi }}_+=\frac{1}{M_+}\sum _{i=1\atop y_i=1}^{M} \,\varvec{\phi }(\mathbf{x}_i), \quad \bar{\varvec{\phi }}_-=\frac{1}{M_-}\sum _{i=1 \atop y_i=-1}^{M} \,\varvec{\phi }(\mathbf{x}_i), \end{aligned}$$
(27)

and \(\bar{\varvec{\phi }}_+\) and \(\bar{\varvec{\phi }}_-\) are the averages of the mapped training data belonging to Classes 1 and 2, respectively, and \(M_+\) and \(M_-\) are the numbers of training data belonging to Classes 1 and 2, respectively.

If \(M_+ = M_-\), \(\mathbf{w}\) is the vector which is from \(\bar{\varvec{\phi }}_-/2\) to \(\bar{\varvec{\phi }}_+/2\). Therefore the decision function is orthogonal to the vector. If \(M_+ \ne M_-\), the decision function is orthogonal to \(\bar{\varvec{\phi }}_+ - (M_-/M_+) \, \bar{\varvec{\phi }}_-\).

Slope Optimization. To control the decision function, we introduce a positive hyperparameter \(C_\mathrm{m}\) as follows:

$$\begin{aligned} \mathbf{w}= & {} \frac{M_+}{M}\bar{\varvec{\phi }}_+-\frac{C_\mathrm{m} \,M_-}{M}\bar{\varvec{\phi }}_-, \end{aligned}$$
(28)

where \(C_\mathrm{m}\) works to lengthen or shorten the length of vector \(\bar{\varvec{\phi }}_-\) according to whether \(C_\mathrm{m}>1\) or \(0< C_\mathrm{m}<1\). Therefore, by changing the value of \(C_\mathrm{m}\), the slope of the decision function is changed.

Then the decision function becomes

$$\begin{aligned} f(\mathbf{x}) = \frac{1}{M}\sum _{i=1,y_i=1}^M K(\mathbf{x}, \mathbf{x}_i)-\frac{C_\mathrm{m}}{M}\sum _{i=1,y_i=-1}^M K(\mathbf{x}, \mathbf{x}_i)+b. \end{aligned}$$
(29)

We determine the value of \(C_\mathrm{m}\) by cross-validation.

In k-fold cross-validation, we divide the training data set into k almost-equal-size subsets and train the classifier using the \(k-1\) subsets and test the trained classifier using the remaining subset. We iterate this procedure k times for different combinations and calculate the classification error.

Calculation of the classification error for a given \(C_\mathrm{m}\) value is as follows:

  1. 1.

    Calculate (29) with \(b=0\) using the \(k-1\) subsets.

  2. 2.

    Calculate the bias term using the method discussed in Sect. 2.3.

  3. 3.

    Calculate the classification error for the remaining subset using the decision function generated in Steps 1 and 2.

Repeat the above procedure for the k different combinations and calculate the classification error for the decision function.

For a given set of \(C_\mathrm{m}\) values, we calculate the classification errors and select the value of \(C_\mathrm{m}\) with the minimum classification error.

2.5 Equality-Constrained MAMCs

To improve the generalization ability of MAMCs further, we consider equality-constrained MAMCs (EMAMCs) as follows:

$$\begin{aligned} \text {maximize}\,\, Q(\mathbf{w},b)=-\frac{1}{2} \mathbf{w}^{\top }\, \mathbf{w} +\frac{C_\mathrm{a}}{M}\sum _{i=1}^{M} y_i \,(\mathbf{w}^{\top } \varvec{\phi }(\mathbf{x}_i)+b)-\frac{C}{2}\sum _{i=1}^M \xi _i^2 \end{aligned}$$
(30)
$$\begin{aligned} \text {subject to}\,\,y_i \,(\mathbf{w}^{\top } \varvec{ \phi }(\mathbf{x}_i)+b)=1-\xi _i\quad \text{ for }\quad i=1,\ldots ,M, \end{aligned}$$
(31)

where \(C_\mathrm{a}\) and C are parameters to control the trade-off between the generalization ability and the classification error for the training data, and \(\xi _i\) are the slack variables for \(\mathbf{x}_i\).

We solve (30) and (31) in the empirical feature space [2] and define

$$\begin{aligned} \varvec{\phi }(\mathbf{x}) = (K(\mathbf{x},\mathbf{x}_1),\ldots ,K(\mathbf{x},\mathbf{x}_M))^{\top }. \end{aligned}$$
(32)

Solving (31) for \(\xi _i\) and substituting it into (30), we obtain the unconstrained optimization problem:

$$\begin{aligned}&\text{ maximize }\quad Q(\mathbf{w},b)=-\frac{1}{2} \mathbf{w}^{\top }\, \mathbf{w} +\frac{C_\mathrm{a}}{M}\sum _{i=1}^{M} y_i \,(\mathbf{w}^{\top } \varvec{ \phi }(\mathbf{x}_i)+b)\nonumber \\&\quad \quad \quad \quad \quad -\frac{C}{2}\sum _{i=1}^M (1-y_i \,(\mathbf{w}^{\top } \varvec{ \phi }(\mathbf{x}_i)+b))^2. \end{aligned}$$
(33)

If we delete the second term (the average margin) in the above equation, the optimization problem result in the least squares (LS) SVM defined in the empirical feature space [2].

Taking the partial derivative of (33) with respect to \(\mathbf{w}\) and b and setting the results to zero, we obtain the optimality conditions:

$$\begin{aligned} \left( {1}+C\sum _{i=1}^M \varvec{\phi }(\mathbf{x}_i)\, \varvec{\phi }^{\top }(\mathbf{x}_i)\right) \mathbf{w}+ C\sum _{i=1}^M y_i \, \varvec{\phi }(\mathbf{x}_i)\,b = \left( \frac{C_\mathrm{a}}{M}+C\right) \sum _{i=1}^M y_i \, \varvec{\phi }(\mathbf{x}_i), \end{aligned}$$
(34)
$$\begin{aligned} C\sum _{i=1}^M \varvec{\phi }(\mathbf{x}_i) \, \mathbf{w} +C\,M \, b =\left( \frac{C_\mathrm{a}}{M}+C\right) \sum _{i=1}^M y_i. \end{aligned}$$
(35)

The above optimality conditions can be solved for \(\mathbf{w}\) and b by matrix inversion. The coefficient \(({C_\mathrm{a}}/{M}+C)\) can be deleted because it is a scaling factor and does not change the decision boundary. Then, because \(C_\mathrm{a}\) is not included in the left-hand sides of (34) and (35), the value of \(C_\mathrm{a}\) does not influence the location of the decision boundary. This means that the second term in (33) can be safely deleted.

In addition, if we delete the \(\mathbf{w}^{\top }\, \mathbf{w}\) term from (33), all the terms in the left-hand sides of (34) and (35) include C, thus C can be deleted; C does not work to control the trade-off. Therefore, the \(\mathbf{w}^{\top }\, \mathbf{w}\) term is essential.

Accordingly, dividing (34) and (35) by C and deleting the constant term \(({C_\mathrm{a}}/{C \, M}+1)\) from the right-hand sides of (34) and (35), we obtain

$$\begin{aligned} \left( \frac{1}{C}+\sum _{i=1}^M \varvec{\phi }(\mathbf{x}_i)\, \varvec{\phi }^{\top }(\mathbf{x}_i)\right) \mathbf{w}+ \sum _{i=1}^M y_i \, \varvec{\phi }(\mathbf{x}_i)\,b =\sum _{i=1}^M y_i \, \varvec{\phi }(\mathbf{x}_i), \end{aligned}$$
(36)
$$\begin{aligned} \sum _{i=1}^M \varvec{\phi }(\mathbf{x}_i) \, \mathbf{w} +M \, b =\sum _{i=1}^M y_i. \end{aligned}$$
(37)

The above formulation is exactly the same as the LS SVM defined in the empirical feature space. Therefore, the EMAMC results in the LS SVM.

3 Performance Evaluation

3.1 Experimental Conditions

We compared the proposed MAMC including the EMAMC (LS SVM) with the plain MAMC and the L1 SVM using two-class data sets [23]. The L1 SVM we used is as follows:

$$\begin{aligned} \text {maximize} \quad Q(\varvec{\alpha }) = \sum _{i=1}^{M}\alpha _{i} - \frac{1}{2}\sum _{i,j=1}^{M}\alpha _{i}\alpha _{j}\,y_{i}\,y_{j} K(\mathbf{x}_{i}, \mathbf{x}_{j}) \end{aligned}$$
(38)
$$\begin{aligned} \text {subject to}\quad \sum _{i=1}^{M}y_{i}\,\alpha _{i}=0, \quad 0 \le \alpha _{i} \le C \quad \text{ for } \quad i=1,...,M, \end{aligned}$$
(39)

where \(\alpha _{i}\) are Lagrange multipliers associated with \(\mathbf{x}_i\) and \(C \,(>0)\) is a margin parameter that controls the trade-off between the classification error of the training data and the generalization ability.

Table 1 lists the numbers of inputs, training data, test data, and data set pairs of two class problems. Each data set pair consists of the training data set and the test data set. We trained classifiers using the training data set and evaluated the performance using the test data set. Then we calculated the average accuracy and the standard deviation for all the data set pairs. We determined the parameter values by fivefold cross-validation. We selected the \(\gamma \) value of the RBF kernels from {0.01, 0.1, 0.5, 1, 5, 10, 15, 20, 50, 100, 200, 300, 400, 500, 600, 700}. For the \(C_\mathrm{m}\), we selected from {0.05, 0.1, 0.2, ...,0.9,1.0,1.1111,..., 20}. For the EMAMC and L1 SVM, we selected the \(\gamma \) value from 0.01 to 200 and the C value, from {0.1, 1, 10, 50, 100, 500, 1000, 2000}. We trained the L1 SVM using SMO-NM [24], which fuses SMO (Sequential minimal optimization) and NM (Newton’s method).

Table 1. Benchmark data sets for two-class problems
Full size table

3.2 Results

Table 2 shows the average accuracies and their standard deviations of the six classifiers with RBF kernels. In the table, MAMC is given by (12) and (13) and the \(\gamma \) value is optimized by cross-validation. In MAMC\(_\mathrm{b}\), the bias term is optimized as discussed in Sect. 2.3. In MAMC\(_\mathrm{bs}\), after \(\gamma \) value is optimized with \(C_\mathrm{m} = 1\), the \(C_m\) value is optimized. We call this strategy line search in contrast to grid search. In MAMC\(_\mathrm{bsg}\), the \(\gamma \) and \(C_\mathrm{m}\) values are optimized by grid search.

Among the six classifiers including the L1 SVM the best average accuracy is shown in bold and the worst average accuracy is underlined. The “Average” row shows the average accuracy of the 13 average accuracies and the two numerals in the parentheses show the numbers of the best and worst accuracies in the order. We performed Welch’s t test with the confidence intervals of 95 %. The “W/T/L” row shows the results; W, T, and L denote the numbers that the MAMC\(_\mathrm{bs}\) shows statistically better than, the same as, and worse than the remaining five classifiers, respectively.

From the “Average” row, the EMAMC performed best in the average accuracy and the L1 SVM the second best. The difference between MAMC\(_\mathrm{bsg}\) and MAMC\(_\mathrm{bs}\) is small. The MAMC is the worst. From the “W/T/L” row, the accuracies of the MAMC\(_\mathrm{bs}\) and the MAMC\(_\mathrm{bsg}\) are statistically comparable and the accuracy of the MAMC\(_\mathrm{bs}\) is slightly better than that of the MAMC\(_\mathrm{b}\) but always better than that of the MAMC. The accuracy of the MAMC\(_\mathrm{bs}\) is worse than that of the EMAMC and L1 SVM.

In Sect. 2.2, we clarified that the bias term is not optimized by the original MAMC formulation. This is exemplified by the experiments. By optimizing the bias term as proposed in Sect. 2.3, the accuracy is improved drastically. The effect of slope optimization to the accuracy is small. However, by the bias term and slope optimization, the generalization ability is still below that of EMAMC or L1 SVM. This indicates that the equality or inequality constraints are essential in realizing the high generalization ability.

Table 2. Accuracy comparison for the two-class problems
Full size table

We measured the average CPU time per data set including time for model selection by fivefold cross-validation, training a classifier, and classifying the test data by the trained classifier. We used a personal computer with 3.4 GHz CPU and 16 GB memory. Table 3 shows the results. From the table the MAMC is the fastest and the MAMC\(_\mathrm{bs}\) and MAMC\(_\mathrm{b}\) are comparable to the MAMC. Comparing the MAMC\(_\mathrm{bs}\) and the MAMC\(_\mathrm{bsg}\), the MAMC\(_\mathrm{bsg}\) requires more time because of the grid search. Because the classification performance is comparable, line search seems to be sufficient. The EMAMC, L1 SVM and MAMC\(_\mathrm{bsg}\) are in the slowest group.

Table 3. Training time comparison for the two-class problems (in seconds)
Full size table

3.3 Discussions

The advantage of the MAMC is its simplicity: The coefficient vector of the decision hyperplane is calculated by addition or subtraction of kernel values. The inferior generalization ability of the original MAMC is mitigated by bias and slope optimization, but the improvement is still not sufficient compared to the EMAMC and L1 SVM. Therefore, the introduction of the equality or inequality constraints are essential. But it leads to the LS SVM or L1 SVM and the simplicity of the MAMC is completely lost.

4 Conclusions

We discussed two ways to improve the generalization ability of the maximum average margin classifier (MAMC). One is to optimize the bias term after calculating the weight vector, and the other is to optimize the slope of the decision function by introducing the weight parameter to the average vector of one class. The parameter value is determined by cross validation. To improve the generalization ability further, we introduced the EMAMC, which is the equality constrained MAMC, but this is shown to be equivalent to the LS SVM defined in the empirical feature space.

According to the experiments for two-class problems, we show that the generalization ability is improved by the bias term and slope optimization. However, the obtained generalization ability is inferior to the EMAMC and L1 SVM. Therefore, the unconstrained MAMC is not so powerful as the EMAMC and L1 SVM.