Graph-Margin Based Multi-label Feature Selection

Abstract

Since instances in multi-label problems are associated with several labels simultaneously, most traditional feature selection algorithms for single label problems are inapplicable. Therefore, new criteria to evaluate features and new methods to model label correlations are needed. In this paper, we adopt the graph model to capture the label correlation, and propose a feature selection algorithm for multi-label problems according to the graph combining with the large margin theory. The proposed multi-label feature selection algorithm GMBA can efficiently utilize the high order label correlation. Experiments on real world data sets demonstrate the effectiveness of the proposed method. The codes of the experiment of this paper are available at https://github.com/Faustus-/ECML2016-GMBA.

1 Introduction

Multi-label learning studies the problem in which each instance is associated with a set of labels simultaneously. It usually occurs in text categorization, automatic annotation and bioinformatics, etc. [24]. For example, each music in emotions [15] data set can be associated with at most six different emotion tags simultaneously. A straightforward method to solve the multi-label problem is to decompose the problem into a series of single label binary classification problems, such as Binary Relevance [2] and ML-kNN [23]. However, this strategy neglects the label correlation which is usually helpful for improving the performance of a multi-label learning algorithm. To complement this, various multi-label learning algorithms with the consideration of label correlation have been proposed, such as [4, 7, 8, 11, 13, 19, 22]. According to the utilization of label correlation, these algorithms can be divided into three orders [24]: (a) the first order algorithms predict labels for an unseen instance one by one. They are very simple while neglecting label correlation [2, 23]. (b) the second order algorithms consider pairwise relation between labels, which usually leads to a label ranking problem [4, 8]. (c) the high order algorithms capture more complex correlation between labels, but they are computationally expensive [7, 11, 13, 19, 22].

Similar to other machine learning tasks, multi-label learning also suffers from the curse of dimensionality. Redundant and irrelevant features make data intractable, resulting in unreliable model and degraded learning performance. Feature selection is an efficient and popular technique to reduce dimensionality. Several feature selection algorithms for the multi-label problem have been presented. For example, feature selection algorithms for multi-label naive bayes classifier and Rank-SVM classifier are introduced in [5, 21] respectively. These multi-label feature selection algorithms belong to the wrapper model [14], which evaluates features according to predictive results of the specified learning algorithm, thus they share bias of the learning algorithm and it is prohibitively expensive to run for data with a large number of features. In [6], two classic single-label feature selection algorithms, F-Statistic and ReliefF, are extended to handle multi-label problems. These algorithms belong to the filter model [14], which evaluates features by measuring the statistics of a multi-label data set. Algorithms belonging to the filter model are independent of specified classifiers and more flexible than those belonging to the wrapper model.

In this paper, a graph-margin based multi-label feature selection algorithm (GMBA) is proposed. GMBA firstly describes multi-label data with a graph, which has good discrimination capability and shares similar expression capability to the hypergraph applied in [13, 19]. Then, it measures features based on the graph combining with the large margin theory. Since GMBA evaluates features according to the graph derived from the training data, it is independent of a specified learning algorithm and belongs to the filter model. We will introduce GMBA in the following order. In Sect. 2, we define a similarity measure for multi-label instances and describe multi-label data by a graph. The discrimination capability and expression capability of the graph are also discussed in this section. In Sect. 3, we define a margin for multi-label data and derive GMBA depending on the graph combining with the margin. In addition, experimental results on real world data sets are reported in Sect. 4 and paper concludes in Sect. 5.

Notations. Before introducing the algorithm, we will give the notations in this paper. $\textit{n}$, $\textit{D}$ and $\textit{Q}$ denote the number of training instances, the data dimensionality, and the number of labels, respectively. $\textit{F}^{d}$ denotes the $\textit{d}$th feature and $\textit{l}^{q}$ denotes the $\textit{q}$th label, where $1 \le \textit{d} \le D$ and $1 \le \textit{q} \le Q$. $\textit{n}_{q}$ denotes the number of training samples associated with $\textit{l}^{q}$. $\left( {{\varvec{x}}}_{i}, {{\varvec{y}}}_{i} \right)$ denotes the $\textit{i}$th instance in the training data.

${{\varvec{x}}}_{i}=\left( \textit{x}_{i}^{1},...,\textit{x}_{i}^{d},...,\textit{x}_{i}^{D}\right)$ denotes the features of the $\textit{i}$th instance in the training data, where $\textit{x}_{i}^{d}$ denotes the $\textit{d}$th component of the $\textit{i}$th instance, or the $\textit{i}$th instance has value $\textit{x}_{i}^{d}$ for $\textit{F}^{d}$.

${{\varvec{x}}}^{d}=\left( \textit{x}_{1}^{d},...,\textit{x}_{i}^{d},...,\textit{x}_{n}^{d}\right) ^{T}$ denotes a feature vector of the $\textit{d}$th feature. The superscript $\textit{T}$ means the transpose of a vector or matrix.

${{\varvec{y}}}_{i}=\left( \textit{y}_{i}^{1},...,\textit{y}_{i}^{q},...,\textit{y}_{i}^{Q}\right)$ denotes the relationship between labels and the $\textit{i}$th instance in the training data. If the $\textit{i}$th instance is associated with $\textit{l}^{q}$ then $\textit{y}_{i}^{q}=1$, or $\textit{y}_{i}^{q}=0$. For single-label problems, there is a constraint that $\left| {{\varvec{y}}}_{i}\right| = 1$, $1 \le \textit{i} \le \textit{n}$, where $\left| \cdot \right|$ denotes the 1-norm of the vector.

$\textit{s}_{\left( i, i^{\prime }\right) }$ denotes the similarity between the $\textit{i}$th and $\textit{i}^{\prime }$th instances.

$\mathbf G = \left( \mathbf V , \mathbf E \right)$ denotes a graph, where $\mathbf V$ and $\mathbf E$ denote the vertex set and the edge set of the graph, respectively. ${{\varvec{A}}}_{G}$ denotes the adjacent matrix of $\mathbf G$, ${{\varvec{D}}}_{G}$ denotes the degree matrix of $\mathbf G$. ${{\varvec{L}}}_{G} = {{\varvec{D}}}_{G} - {{\varvec{A}}}_{G}$ is the corresponding Laplacian matrix.

$\left[ \pi \right]$ returns 1 if predicate $\pi$ holds, and 0 otherwise.

$\left| \cdot \right|$ and $\left\| \cdot \right\|$ returns 1-norm and 2-norm respectively.

$\varvec{\omega }$ is a weight vector of features.

2 Graph Model for Multi-label Data

2.1 Graph Definition

Graph is a widely used model for its powerful expression capability. For example, well-known page rank and image segmentation algorithm in [3] are based on the graph model. In this paper, we adopt the graph to capture the correlation between labels and instances for multi-label data.

Suppose, in a graph, each vertex $\textit{v}_{i} \in \mathbf V$ represents an instance and an edge $\textit{e}_{\left( i, i^{\prime } \right) } \in \mathbf E$ connecting two vertexes denotes the similarity of the corresponding instances, then a simple undirected graph $\mathbf G = \left( \mathbf V , \mathbf E \right)$ can be built to model the correlation between instances. The key of building the graph depends on how one measures the instance similarity. For a single-label problem, the similarity between two instances ${{\varvec{x}}}_i$ and ${{\varvec{x}}}_{i ^{\prime }}$ are usually defined as Eq. 1 [25].

$$\begin{aligned} \begin{aligned} \textit{s}_{single}\left( i, i^{\prime }\right) = {\left\{ \begin{array}{ll} \frac{1}{\textit{n}_{q}}, &{}\textit{y}_{i}^{q}=\textit{y}_{i^{\prime }}^{q}=1\\ 0, &{}otherwise \end{array}\right. } \end{aligned} \end{aligned}$$

(1)

which means that instances in the same class share the same similarity, while similarity between instances from different classes is 0. However, when it comes to multi-label problems, an instance is associated with several labels (classes) simultaneously and it is ambiguous to compare the belongingness of two different instances. Therefore, Eq. (1) is not suitable when solving multi-label problems and we define Eq. 2 to measure the similarity between two multi-label instances.

$$\begin{aligned} \begin{aligned} \textit{s}_{multi}\left( i,i^{\prime }\right) = {\left\{ \begin{array}{ll} \frac{\sum _{\textit{q}=1}^{Q} \textit{n}_{q} \cdot \left[ \textit{y}_{i}^{q} = 1 \wedge \textit{y}_{i^{\prime }}^{q} = 1\right] }{\sum _{\textit{q}=1}^{Q}{} \textit{n}_{q} \cdot \left[ \textit{y}_{i}^{q} = 1 \vee \textit{y}_{i^{\prime }}^{q} = 1\right] } , &{} \sum _{\textit{q}=1}^{Q}{} \textit{n}_{q} \cdot \left[ \textit{y}_{i}^{q} = 1 \vee \textit{y}_{i^{\prime }}^{q} = 1\right] \ne 0 \\ 0, &{} otherwise \end{array}\right. } \end{aligned} \end{aligned}$$

(2)

In Eq. 2, the numerator counts the labels two instances shared, and the denominator counts the labels at least one of the two instances associated with. $\textit{n}_{q}$ is the number of training samples associated with $\textit{l}_{q}$ and it is applied as a weight to tune the importance of different labels. Equation 2 is a variation of the Jaccard similarity, which measures the ratio of the size of intersection and the size of union for two sets. Then, the multi-label data can be represented as a graph using an adjacent matrix ${{\varvec{A}}}_{G}$ definded in Eq. 3, where $\textit{A}_{G}\left( i,i^{\prime }\right)$ is the element in the $\textit{i}$th row, $\textit{i}^{\prime }$th column of ${{\varvec{A}}}_{G}$.

$$\begin{aligned} \begin{aligned} \textit{A}_{G}\left( i,i^{\prime }\right) = {\left\{ \begin{array}{ll} \textit{s}_{multi}\left( i, i^{\prime }\right) , &{} i \ne i^{\prime }\\ 0, &{} otherwise \end{array}\right. } \end{aligned} \end{aligned}$$

(3)

2.2 Discrimination Capability

To explain the discrimination capability of the proposed graph, an example is presented below. Assuming that there are $\textit{Q}$ different labels, we have ${{\varvec{y}}}_{i} \in \left\{ 0, 1\right\} ^{Q}$. Without loss of generality, we set $\textit{Q}=2$ and two labels are named $\textit{l}^{1}$ and $\textit{l}^{2}$. We also assume that a multi-label training data set consists of one instance associated with $\textit{l}^{1}$, two instances associated with $\textit{l}^{2}$, one instance associated with $\textit{l}^{1}$ and $\textit{l}^{2}$ simultaneously and two instances associated with no labels. The proposed graph to describe these instances is given in Fig. 1(a). Then, if one can split the graph into different parts (such as the ellipses of dash line), instances associated with different labels will be discriminated. Hence multi-label instances are discriminable in the proposed graph. Moreover, some off the shelf algorithms can be applied to finish this task, such as normalized cut [12], ration cut [18], etc.

Fig. 1.

(a) Our proposed graph for multi-label data, (b) The graph for multi-class data transformed from the multi-label data. The edges in graphs are denoted with solid lines and circles are vertexes. The fractions on the edges represent the similarity weight. Circles fallen in the same ellipse (dash line) represent instances associated with the same label/class. The circle fallen in the intersection of two ellipses means the instance is associated with two labels simultaneously. And the two instances associated with no labels are put in the ellipse below.

In addition, the discrimination capability of the proposed graph is similar to the one derived from label power set algorithms as in [16, 17], while the proposed graph is smoother and can capture label correlation. More specifically, a label power set algorithm usually transforms a multi-label problem into a multi-class problem in which each class corresponds to a label power set. For the multi-label problem mentioned above, a label power set algorithm will transform it into a multi-class problem with 4 different classes: $\emptyset$, $\left\{ \textit{l}^{1}\right\}$, $\left\{ \textit{l}^{2}\right\}$ and $\left\{ \textit{l}^{1}, \textit{l}^{2} \right\}$, and each instance is associated with one class. Since a multi-class problem belongs to the single-label learning problem, the similarity between instances can be measured by Eq. 1. The resulting graph is shown in Fig. 1(b), which includes 4 unconnected subgraphs. The partitions of the graph (ellipses of dash line) are similar to the ones in Fig. 1(a), hence they have similar discrimination capability. However, in multi-class problems, the similarity between instances from different classes is 0, and there are no edges connecting them, such as the instance belonging to the class $\left\{ \textit{l}^{1}\right\}$ and the one belonging to the class $\left\{ \textit{l}^{1}, \textit{l}^{2} \right\}$ in Fig. 1(b). Although these instances actually share some labels in common, such as the label $\textit{l}^{1}$ for the class $\left\{ \textit{l}^{1}\right\}$ and the class $\left\{ \textit{l}^{1}, \textit{l}^{2} \right\}$, the correlation is not considered by the graph in Fig. 1(b). On the contrary, such kind of correlation is considered in our graph as in Fig. 1(a) through the edges weight between 0 and 1. Therefore, the proposed graph for a multi-label problem is smoother than the graph for a multi-class problem transformed from a multi-label problem in [16, 17] and can capture label correlation.

2.3 Expression Capability

Though the proposed graph in Sect. 2.1 is a simple-graph, it has similar expression capability to a hypergraph, which has been successfully applied to capture high order label correlation in [13, 19].

Different from edges in a simple-graph, an edge, which is called hyperedge, in a hypergraph connects more than two vertexes simultaneously. Hence multi-label data can be described by a hypergraph as follows: in a hypergraph $\mathbf G _{H} = \left( \mathbf V _{H}, \mathbf E _{H} \right)$, each vertex $\textit{v}_{i} \in \mathbf V _{H}$ corresponds to an instance in the multi-label data set, each hyperedge $\textit{e}_{q} \in \mathbf E _{H}$ is a subset of $\mathbf V _{H}$, where $\textit{e}_{q} = \{ \textit{v}_{i} \mid \textit{y}_{i}^{q} = 1, 1 \le \textit{i} \le \textit{n} \}$. The degree of each hyperedge $\textit{d} \left( \textit{e}_{q} \right)$ is defined as the number of vertexes on that hyperedge, namely $\textit{n}_{q}$, and we may set the weight of a edge, $\textit{w} \left( \textit{e}_{q} \right)$, equals to its degree.

If we apply Clique Expansion [1, 13, 19] to expand the hypergraph above, we obtain a simple-graph $\mathbf G _{C} = \left( \mathbf V _{C}, \mathbf E _{C} \right)$, where $\mathbf V _{C} = \mathbf V _{H}$ and $\mathbf E _{C} = \{ \textit{e}_{\left( {i}, {i^{\prime }} \right) } \mid \textit{v}_{i} \in \textit{e}_{q} \wedge \textit{v}_{i^{\prime }} \in \textit{e}_{q}, \textit{e}_{q} \in \mathbf E _{H} \}$. The weight of $\textit{e}_{\left( {i}, {i^{\prime }} \right) }$ is defined as Eq. 4.

$$\begin{aligned} \begin{aligned} \textit{w} \left( \textit{e}_{\left( {i}, {i^{\prime }} \right) } \right) = \sum _{\textit{v}_{i} \in \textit{e}_{q} \wedge \textit{v}_{i^{\prime }} \in \textit{e}_{q}, \textit{e}_{q} \in \mathbf E _{H}} \textit{w} \left( \textit{e}_{q} \right) = \sum _{\textit{q}=1}^{Q} \textit{n}_{q} \cdot \left[ \textit{y}_{i}^{q} = 1 \wedge \textit{y}_{i^{\prime }}^{q} = 1\right] \end{aligned} \end{aligned}$$

(4)

Normalizing it to obtain Eq. 5, we find that Eq. 5 is the same to the similarity defined in Eq. 2

$$\begin{aligned} \begin{aligned} \hat{\textit{w}} \left( \textit{e}_{\left( {i}, {i^{\prime }} \right) } \right) = \frac{\sum _{\textit{v}_{i} \in \textit{e}_{q} \wedge \textit{v}_{i^{\prime }} \in \textit{e}_{q}, \textit{e}_{q} \in \mathbf E _{H}} \textit{w} \left( \textit{e}_{q} \right) }{\sum _{\textit{v}_{i} \in \textit{e}_{q} \vee \textit{v}_{i^{\prime }} \in \textit{e}_{q}, \textit{e}_{q} \in \mathbf E _{H}}{} \textit{w} \left( \textit{e}_{q} \right) } = \frac{\sum _{\textit{q}=1}^{Q} \textit{n}_{q} \cdot \left[ \textit{y}_{i}^{q} = 1 \wedge \textit{y}_{i^{\prime }}^{q} = 1\right] }{\sum _{\textit{q}=1}^{Q}{} \textit{n}_{q} \cdot \left[ \textit{y}_{i}^{q} = 1 \vee \textit{y}_{i^{\prime }}^{q} = 1\right] } \end{aligned} \end{aligned}$$

(5)

Thus our proposed graph is the same to the simple-graph expanded from a hypergraph by Clique Expansion. According to [1, 13], both the hypergraph and the expanded simple-graph, as well as the proposed graph, can capture similar high order correlation and therefore they share similar expression capability for multi-label data.

3 Graph-Margin Based Multi-label Feature Selection (GMBA)

In Sect. 2, we propose a discriminative graph to describe multi-label data. According to the similarity measure defined in Eq. 2, the graph reflects the relations of data in label space. However, these relations in label space are usually different from the one in feature space. We will illustrate this case in Fig. 2(a) and (b). For an instance denoted by star in Fig. 2(a), its several nearest neighbors in label space are represented by squares. That is to say, the similarity measured by Eq. 2 between a square and the star is greater than a threshold $\textit{s}_{min}$, and these squares are the closest instances to the star in the proposed graph as in Fig. 2(a). However, if we estimate similarities among instances in feature space, such as using a radial basis function, an instance represented by triangle could be more similar (closer) to the star than squares. This means that the graph built in feature space as in Fig. 2(b) is inconsistent with the graph in label space as in Fig. 2(a).

Fig. 2.

A comparison of graphs built in different spaces. Each star, square or triangle represents an instance. The edges connect two different shapes denote the similarity between them. The shorter an edge is, the more similar two instances are. We omit the edges that do not connect with the star.

Furthermore, for classification problems, the target of a classifier is using features to divide instances into different classes, which means that we have to use features to predict the partitions of the graph in label space. Although the graph built in label space is discriminative as analyzed in Sect. 2.2, an inconsistent counterpart in feature space does not maintain its discrimination power and may lead to wrong partition. Thus we propose a multi-label feature selection algorithm GMBA, which will choose a subset of features that the graph built in this feature subspace, as in Fig. 2(c), is similar to the one in label space, as Fig. 2(a). In addition, a margin, as depicted in Fig. 2(c), is applied in GMBA to guarantee the generalization capability of the selected features.

3.1 Loss Function

To evaluate the inconsistency described above, we design a loss function based on margin. Firstly, we apply $\textit{sim}\left( i\right)$ and $\textit{dissim} \left( i\right)$ to represent the instance subsets similar and dissimilar to $\left( {{\varvec{x}}}_{i}, {{\varvec{y}}}_{i} \right)$ in label space respectively. They are described in Eqs. 6 and 7.

$$\begin{aligned} sim\left( \textit{i}\right) =\left\{ \left( {{\varvec{x}}}_{i^{\prime }},{{\varvec{y}}}_{i^{\prime }}\right) \mid \textit{s}_{multi}\left( i, i^{\prime }\right) \ge \textit{s}_{min}, 1 \le i^{\prime } \le \textit{n} \text { and }i \ne i^{\prime } \right\} \end{aligned}$$

(6)

$$\begin{aligned} dissim\left( \textit{i}\right) =\left\{ \left( {{\varvec{x}}}_{i^{\prime }},{{\varvec{y}}}_{i^{\prime }}\right) \mid \textit{s}_{multi}\left( i, i^{\prime }\right) < \textit{s}_{min}, 1 \le i^{\prime } \le \textit{n} \text { and }i \ne i^{\prime } \right\} \end{aligned}$$

(7)

where $\textit{s}_{min}$ is a given threshold and $\textit{s}_{multi}\left( i, i^{\prime }\right)$ is the similarity defined in Eq. 2. Then, the loss function is designed in Eq. 8 to evaluate the inconsistency between the graph in label space and the one in feature space for $\left( {{\varvec{x}}}_{i}, {{\varvec{y}}}_{i} \right)$.

$$\begin{aligned} Loss\left( i \right) = \sum _{i^{\prime } \in neighbor \left( i \right) } \textit{s}_{multi}\left( i, i^{\prime } \right) \left\| {{\varvec{x}}}_{i} - {{\varvec{x}}}_{i^{\prime }} \right\| ^{2} + \lambda \sum _{i^{\prime \prime } \in dissim \left( i \right) } \delta \left( i^{\prime }, i^{\prime \prime } \right) \end{aligned}$$

(8)

where $neighbor \left( i \right)$ denotes a instance subset with $\textit{k}$ instances those are both nearest to $\left( {{\varvec{x}}}_{i}, {{\varvec{y}}}_{i} \right)$ in feature space and belong to $\textit{sim}\left( i\right)$. The first term of Eq. 8 penalizes large distance between $\left( {{\varvec{x}}}_{i}, {{\varvec{y}}}_{i} \right)$ and its neighbors $\left( {{\varvec{x}}}_{i^{\prime }}, {{\varvec{y}}}_{i^{\prime }} \right)$ in $\textit{neighbor} \left( i \right)$. The second term $\delta \left( i^{\prime }, i^{\prime \prime } \right)$ is a penalty defined in Eq. 9 and $\lambda$ is the tuning parameter.

$$\begin{aligned} \begin{aligned}&\delta \left( i^{\prime }, i^{\prime \prime } \right) =\\&\left( s_{multi}\left( i, i^{\prime } \right) - s_{multi}\left( i, i^{\prime \prime } \right) \right) \cdot \max \left( 0, m \left( i\right) + \left\| {{\varvec{x}}}_{i} - {{\varvec{x}}}_{i^{\prime }} \right\| ^{2} - \left\| {{\varvec{x}}}_{i} - {{\varvec{x}}}_{i^{\prime \prime }} \right\| ^{2} \right) \end{aligned} \end{aligned}$$

(9)

$\delta \left( i^{\prime }, i^{i ^{\prime \prime } } \right)$ is the hinge loss penalizing $\left( {{\varvec{x}}}_{i^{\prime \prime }}, {{\varvec{y}}}_{i^{\prime \prime }} \right)$, which is an instancec in $\textit{dissmiss}\left( i\right)$ but closer to $\left( {{\varvec{x}}}_{i}, {{\varvec{y}}}_{i} \right)$ than $\left( {{\varvec{x}}}_{i^{\prime }}, {{\varvec{y}}}_{i^{\prime }} \right)$ to $\left( {{\varvec{x}}}_{i}, {{\varvec{y}}}_{i} \right)$ in feature space. The closer $\left( {{\varvec{x}}}_{i^{\prime \prime }}, {{\varvec{y}}}_{i^{\prime \prime }} \right)$ to $\left( {{\varvec{x}}}_{i}, {{\varvec{y}}}_{i} \right)$ in feature space and more dissimilar $\left( {{\varvec{x}}}_{i^{\prime \prime }}, {{\varvec{y}}}_{i^{\prime \prime }} \right)$ to $\left( {{\varvec{x}}}_{i}, {{\varvec{y}}}_{i} \right)$ in label space, the larger the penalty. $m \left( i\right)$ is the margin defined in Eq. 10, where $\text {nh} \left( i \right)$ and $\text {nm} \left( i \right)$ are the nearest instances from $sim\left( i\right)$ and $dissim\left( i\right)$ respectively to the $\left( {{\varvec{x}}}_{i}, {{\varvec{y}}}_{i} \right)$ in feature spaces.

$$\begin{aligned} m\left( i \right) =\left| \left\| {{\varvec{x}}}_{i} - {{\varvec{x}}}_{\text {nh} \left( i \right) } \right\| ^{2} - \left\| {{\varvec{x}}}_{i} - {{\varvec{x}}}_{\text {nm} \left( i \right) } \right\| ^{2}\right| \end{aligned}$$

(10)

We will illustrate the penalty defined Eq. 9 for the case depicted in Fig. 2(b). Assuming that the star represents $\left( {{\varvec{x}}}_{i}, {{\varvec{y}}}_{i} \right)$, the margin $m\left( i \right)$ is the absolute value of the square Euclidean distance between the square marked $\textit{nh}$ and the star minus the square Euclidean distance between the triangle marked $\textit{nm}$ and the star. If the square Euclidean distance between any triangle and the star is smaller than the square Euclidean distance between a square and the star plus this margin, it will be penalized by Eq. 9.

3.2 Feature Ranking

Based on the loss function in Eq. 8, one can evaluate the inconsistency between the graph in label space and the one in feature space by summing up the loss of all training data as depicted in Eq. 11. The smaller Eq. 11 is, the more consistent two graphs are. In addition, for feature selection, it is key to find a feature subspace that minimize Eq. 11.

$$\begin{aligned} Loss\left( \mathbf G \right) = \sum _{i=1}^{n} Loss\left( i \right) \end{aligned}$$

(11)

However, it suffers from the complexity of $\textit{O} \left( 2^{\textit{D}}\right)$ to find the best subspace for Eq. 11. As a result, according to [9, 10], we evaluate the fitness of features by a weight vector $\varvec{\omega }$ and find the best $\varvec{\omega }$ by gradient descent method. Specifically, searching for the best $\varvec{\omega }$ can be formulated as Eq. 12

$$\begin{aligned} \min _{\varvec{\omega }} Loss\left( \varvec{\omega }, \mathbf G \right) = \min _{\varvec{\omega }} \sum _{i=1}^{n} Loss\left( \varvec{\omega }. i \right) \end{aligned}$$

(12)

where

$$\begin{aligned} Loss\left( \varvec{\omega }. i \right) = \sum _{i^{\prime } \in neighbor \left( i \right) } \textit{s}_{multi}\left( i, i^{\prime } \right) \left\| {{\varvec{x}}}_{i} - {{\varvec{x}}}_{i^{\prime }} \right\| _{\varvec{\omega } } ^{2} + \lambda \sum _{i^{\prime \prime } \in dissim\left( i \right) }\delta \left( \varvec{\omega }, i^{\prime }, i^{\prime \prime } \right) \end{aligned}$$

(13)

$$\begin{aligned} \begin{aligned}&\delta \left( \varvec{\omega }, i^{\prime }, i^{\prime \prime } \right) \\&= \left( s_{multi}\left( i, i^{\prime } \right) - s_{multi}\left( i, i^{\prime \prime } \right) \right) \cdot \max \left( 0, m \left( i\right) + \left\| {{\varvec{x}}}_{i} - {{\varvec{x}}}_{i^{\prime }} \right\| _{\varvec{\omega }}^{2} - \left\| {{\varvec{x}}}_{i} - {{\varvec{x}}}_{i^{\prime \prime }} \right\| _{\varvec{\omega }}^{2} \right) \end{aligned} \end{aligned}$$

(14)

and $\left\| {{\varvec{z}}}\right\| _{\varvec{\omega }} = \sqrt{\sum _{d=1}^{D} \left( \omega ^{d} \textit{z}^{d} \right) ^{2}}$.

Then Eq. 12 can be solved by the gradient descent and the algorithm is summarized as follows.

Step 1: Initialize $\varvec{\omega } = \left( 1, 1, 1, ... , 1\right)$, and set the number of iterations I.

Step 2: For i =1, 2, ... , I.

(a) Pick up an instance $\left( {{\varvec{x}}}_{i}, {{\varvec{y}}}_{i} \right)$, and find $\textit{sim}\left( i\right)$ and $\textit{dissim}\left( i\right)$ according to Eqs. 2, 6 and 7.

(b) Find k nearest instances to $\left( {{\varvec{x}}}_{i}, {{\varvec{y}}}_{i} \right)$ in feature space from $\textit{sim}\left( i\right)$ as $\textit{neighbor}\left( i\right)$.

(c) Find nh$\left( i\right)$ and nm$\left( i\right)$ from $\textit{sim}\left( i\right)$ and $\textit{dissim}\left( i\right)$ respectively.

(d) Calculate $\textit{m} \left( i\right)$ according to Eq. 10

(e) For d =1, 2, ... , D

$~~~~~~\nabla ^{d} = 2 \omega ^{d} \sum _{i^{\prime } \in \textit{neighbor} \left( i \right) } \textit{s}_{multi}\left( i, i^{\prime } \right) \left\| \textit{x}_{i}^{d} - \textit{x}_{i^{\prime }}^{d} \right\| ^{2} + \lambda \sum _{i^{\prime } \in dissim\left( i\right) } \frac{\partial \delta \left( \varvec{\omega }, i^{\prime }, i^{\prime \prime } \right) }{\partial \omega ^{d}}$,

where $\frac{\partial \delta \left( \varvec{\omega }, i^{\prime }, i^{\prime \prime } \right) }{\partial \omega ^{d}}$ is the partial derivative of $\delta \left( \varvec{\omega }, i^{\prime }, i^{\prime \prime } \right)$ given in Eqs. 15 and 16

$$\begin{aligned} \begin{aligned} \frac{\partial \delta \left( \varvec{\omega }, i^{\prime }, i^{\prime \prime } \right) }{\partial \omega ^{d}}= {\left\{ \begin{array}{ll} 0,&{} m\left( i \right) + \left\| {{\varvec{x}}}_{i} - {{\varvec{x}}}_{i^{\prime }} \right\| ^{2} < \left\| {{\varvec{x}}}_{i} - {{\varvec{x}}}_{i^{\prime \prime }} \right\| ^{2} \\ \textit{diff}\left( d\right) ,&{}otherwise \end{array}\right. } \end{aligned} \end{aligned}$$

(15)

$$\begin{aligned} \textit{diff}\left( d\right) =2\omega ^{d} \left( s_{multi}\left( i, i^{\prime } \right) - s_{multi}\left( i, i^{\prime \prime } \right) \right) \left( \left\| \textit{x}_{i}^{d} - \textit{x}_{i^{\prime }}^{d}\right\| ^{2}-\left\| \textit{x}_{i}^{d} - \textit{x}_{i^{\prime \prime }}^{d}\right\| ^{2} \right) \end{aligned}$$

(16)

(f)$\varvec{\omega } = \varvec{\omega } - \beta \varvec{\nabla }/ \left\| \varvec{\nabla } \right\|$, where $\beta$ is a decay factor.

Step 3: Ranking features based on $\varvec{\omega }$. The greater the $\omega ^{d}$, the better the $\textit{F}^{d}$.

4 Experiments

To demonstrate the effectiveness of the proposed GMBA, we empirically compare the GMBA with the multi-label F-Statistic (MLFS)[6] and the multi-label ReliefF (MLRF) [6].

In addition, spectral feature selection framework (SPEC) [25] is an algorithm which selects features based on the graph structure for single label problems. It measures features according to Eq. 17.

$$\begin{aligned} \begin{aligned} \phi \left( \textit{F}^{d}\right) = \left( \hat{ {{\varvec{x}}}}^{d} \right) ^{T} \varvec{\mathcal {L}_{G}} \hat{ {{\varvec{x}}}}^{d} = \sum _{1 \le i, \textit{i}^{\prime } \le \textit{n}} \frac{\textit{s}_{single}\left( \textit{i}, \textit{i}^{\prime } \right) }{\sqrt{\textit{d}\left( i\right) \textit{d}\left( i^{\prime } \right) }} \left\| \hat{\textit{x}}_{i}^{d} - \hat{\textit{x}}_{i^{\prime }}^{d} \right\| ^{2} \end{aligned} \end{aligned}$$

(17)

where $\textit{d}\left( i\right)$ is the degree of vertex $\textit{v}_i$, $\hat{ {{\varvec{x}}}}^{d}=\frac{{{\varvec{D}}}^{\frac{1}{2}}{{\varvec{x}}}^{d}}{\left\| {{\varvec{D}}}^{\frac{1}{2}}{{\varvec{x}}}^{d}\right\| }$ is the normalized feature vector and $\varvec{\mathcal {L}_{G}} = {{\varvec{D}}}^{-\frac{1}{2}}_{G}{{\varvec{L}}}_{G} {{\varvec{D}}}^{-\frac{1}{2}}_{G}$ is the normalized Laplacian matrix. The smaller the Eq. 17, the better the $\textit{F}^{d}$. We adapt it to multi-label problems by replacing the $\textit{s}_{single}\left( \textit{i}, \textit{i}^{\prime } \right)$ with the proposed similarity $\textit{s}_{multi}\left( \textit{i}, \textit{i}^{\prime } \right)$, so that it will select features consistent with the proposed graph structure for multi-label data.

4.1 Data Sets

Eight benchmark multi-label data sets from different domains are used for experiments, which are downloaded from MULAN¹. Details about data sets are listed in Table 1. All numerical features are normalized with zero mean and unit variance in experiments. Features with variance 0 are eliminated.

Table 1. Summary of 8 benchmark data sets

4.2 Classifiers and Parameters

Binary Relevance [2] ($1_{st}$ order algorithm) and Classifier Chain [11] (high order algorithm) are used as multi-label learning strategy respectively, 3-Nearest Neighbor (3-NN) classifier in scikit-learn² is applied as the base classifier. Number of neighbors for MLRF and $neighbor\left( i\right)$ in GMBA are set 3. The threshold $s_{min}$ and tuning parameter $\lambda$ are 1. The number of iterations I equals to the number of training data n. The decay factor $\beta$ is 0.9. Experiments³ are carried on under the environment of Python 2.7.

4.3 Evaluations

Three different measurements [24], i.e., Hamming loss ($\downarrow$), micro ($\uparrow$) and macro ($\uparrow$) F1-Measure, are applied to validate the performance of the selected features for multi-label learning. ($\downarrow$) denotes the smaller the better, while ($\uparrow$) denotes the larger the better. Except for mediamill and bibtex, all results reported in this paper are the average of 10-cross validation. Since the big size of mediamill and bibtex, we randomly select 1800 instances and other 10 percent of total instances for training and testing respectively. The results reported are the average of 10 trials of experiments.

4.4 Results

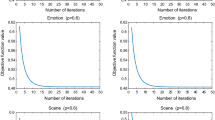
Experimental results are shown in Figs. 3, 4, 5 and 6. For space limitation, we display the Hamming Loss for the bibtex, emotions, enron and genebase, macro F1-Measure metrics for mediamill, medical, scene and yeast when the multi-label learning strategy is Binary Relevance. We also display the Hamming Loss for mediamill, medical, scene and yeast, macro F1-Measure metrics for bibtex, emotions, enron and genebase when the multi-label learning strategy is Classifier Chain. Complete results of micro F1-Measure metrics are displayed in Figs. 5 and 6.

Experimental results show that features selected by proposed GMBA obtain better classifying performance than others in most cases. For emotions and scene data sets, all algorithms achieve similar performance, which might result from the fact that there are only 6 labels, causing a weak discrimination power of graphs built in the label space. In addition, GMBA and the adapted SPEC are suitable for more data sets than MLFS and MLRF, since the performance of MLFS and MLRF vary from different data sets.

Fig. 3.

Hamming loss ($\downarrow$). The first 4 diagrams show the hamming loss of applying the Binary Relevance while the rest show the results from the Classifier Chain. Y-axis corresponds to different metrics and X-axis denotes the percentage of features selected. The horizontal lines are the results of classifying with all features

Fig. 4.

macro F1-Measure ($\uparrow$). The first 4 diagrams show the macro F1-Measure of applying the Binary Relevance while the rest show the results from the Classifier Chain. Y-axis corresponds to different metrics and X-axis denotes the percentage of features selected. The horizontal lines are the results of classifying with all features

Fig. 5.

The micro F1-Measure ($\uparrow$) of applying the Binary Relevance. Y-axis corresponds to the metrics and X-axis denotes the percentage of features selected. The horizontal lines are the results of classifying with all features

Fig. 6.

The micro F1-Measure ($\uparrow$) of applying the Classifier Chain. Y-axis corresponds to the metrics and X-axis denotes the percentage of features selected. The horizontal lines are the results of classifying with all features

5 Discussions and Conclusions

According to experimental results, GMBA performs better than other algorithms, and both GMBA and SPEC are suitable for more data sets than MLFS and MLRF. In addition, while GMBA and SPEC all aim to find a feature subset that the graph built in this subspace is consistent with the graph built in label space, GMBA is superior to the SPEC in most cases. This results from the margin we applied in GMBA, since a margin usually leads to better discrimination and generalization, such as LMNN in [20] and the classic SVM. More specifically, as illustrated in Fig. 2(c), similar instances are $\textit{pushed}$ close to each other and dissimilar instances are $\textit{pulled}$ away from them according to the margin. In this way, the margin makes features in this subspace become more discriminative.

In conclusion, based on the graph and the large margin theory, the proposed GMBA can capture high order label correlation and guarantee generalization capability. Experimental results on different real world data sets indicate the effectiveness and good performance of the proposed algorithm.