Abstract
Complex active systems have been proposed as a formalism for modeling real dynamic systems that are organized in a hierarchy of behavioral abstractions. As such, they constitute a conceptual evolution of active systems, a class of discrete-event systems introduced into the literature two decades ago. A complex active system is a hierarchy of active systems, each one characterized by its own behavior expressed by the interaction of several communicating automata. The interaction between active systems within the hierarchy is based on special events, which are generated when specific behavioral patterns occur. Recently, the task of diagnosis of complex active systems has been studied, with an efficient diagnosis technique being proposed. However, the observation of the system is assumed to be linear and certain, which turns out to be an over-assumption in real, large, and distributed systems. This paper extends diagnosis of complex active systems to cope with uncertain temporal observations. An uncertain temporal observation is a DAG where nodes are marked by candidate labels (logical uncertainty), whereas arcs denote partial temporal ordering between nodes (temporal uncertainty). By means of indexing techniques, despite the uncertainty of temporal observations, the intrinsic efficiency of the diagnosis task is retained in both time and space.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Often, dynamic systems can be modeled as discrete-event systems [4]. Seminal works on diagnosis of discrete-event systems (DES’s) maximize offline preprocessing in order to generate an efficient online diagnoser [20, 21]. However, this requires generating the global DES model, which is bound to be impractical for large and distributed systems.
Other approaches, like diagnosis of active systems (AS’s) [1, 13, 15], avoid generating the global model of the system by reconstructing online only the behavior which is consistent with the observation. Still, in the worst case, the number of behavior states is exponential with the number of components. This is why efficient techniques need to be designed in order to mitigate the explosion of the reconstructed behavior.
This paper deals with diagnosis of a class of DES’s called complex active systems (CAS’s), based on a class of observations called uncertain temporal observations.
In the literature, the term complex system is used to encompass a research approach to problems in a variety of disciplines [2, 6–8, 10, 19, 22]. Generally speaking, a complex system is a group or organization which is made up of many interacting components. In a complex system, interactions between components lead to an emergent behavior, which is unpredictable from a knowledge of the behavior of the individual components only. Inspired by complex systems in nature and society, complexity has been injected into the modeling and diagnosis of active systems [13], a special class of discrete-event systems [4], which are modeled as networks of interacting components, where the behavior of each component is described by a communicating automaton [3]. To this end, the notion of context-sensitive diagnosis was first introduced in [14] and then extended in [18], for active systems that are organized within abstraction hierarchies, so that candidate diagnoses can be generated at different abstraction levels. Active systems have been equipped with behavior stratification [16, 17], where different networks of components are accommodated within a hierarchy. This resembles emergent behavior that arises from the vertical interaction of a network with superior levels based on pattern events. Pattern events occur when a network performs strings of component transitions matching patterns which are specific to the application domain. Complex patterns are also considered in research on cognitive systems [5, 23, 24].
Recently, diagnosis of complex active systems has been addressed, with an efficient diagnosis technique being proposed [11]. However, the observation of the system is assumed to be linear and certain, which turns out to be an over-assumption in real, large, and distributed systems. This paper extends diagnosis of complex active systems to cope with uncertainty in temporal observations. An uncertain temporal observation is a DAG where nodes are marked by candidate labels, whereas arcs denote partial temporal ordering, as proposed in [12] for diagnosis of (plain) active systems. In virtue of specific indexing techniques, the efficiency of the diagnosis task introduced in [11] is kept in both time and space when uncertain temporal observations come into play.
2 Active Systems
An active system A is a network of components, each one being defined by a topological model and a behavioral model. The topological model embodies a set of input terminals and a set of output terminals. The behavioral model is a communicating automaton where each state transition is triggered by an event ready at one input terminal. When triggered, the transition may generate events at some output terminals. Since each output terminal of a component c is connected with the input terminal of another component \(c'\), a transition in c may cause the triggering of a transition in \(c'\). More generally, since components in A form a network, one single transition in one component may result in a reaction of A involving several (possibly all) components in A.
Example 1
Displayed in Fig. 1 are the topological models (top) and behavioral models (bottom) of sensor and breaker. The connection of output terminal O of sensor with input terminal I of breaker gives rise to an active-system model, namely Protection, outlined on the left-hand side of Fig. 2. An active system P is obtained as an instantiation of Protection model, which requires the instantiations of sensor and breaker component models by relevant components, namely s and b, respectively, as outlined in the right-hand side of Fig. 2. We assume that active system P is designed to protect one side of a power transmission line from short circuits. To this end, sensor s detects variation in voltage, possibly commanding breaker b to either open or close. Transitions in behavioral models are detailed below, where event e at terminal t is written e(t):
-
(Sensor) \(s_1\) detects low voltage and outputs \({ op }(O)\); \(s_2\) detects normal voltage and outputs \({ cl }(O)\); \(s_3\) detects low voltage, yet outputs \({ cl }(O)\); \(s_4\) detects normal voltage, yet outputs \({ op }(O)\);
-
(Breaker) \(b_1\) consumes \({ op }(I)\) and opens; \(b_2\) consumes \({ cl }(I)\) and closes; \(b_3\) consumes \({ op }(I)\), yet keeps being closed; \(b_4\) consumes \({ cl }(I)\), yet keeps being closed; \(b_5\) consumes \({ cl }(I)\); \(b_6\) consumes \({ op }(I)\).
An active system (AS) A can be either quiescent or reacting. If quiescent, no event occurs and, consequently, no transition is performed. A becomes reacting when an external event occurs, which can be consumed by a component in A. When reacting, the occurrence of a component transition moves A to a new state, with each state being a pair \(({\mathbb {S}}, {\mathbb {E}})\), where \({\mathbb {S}}= (s_1, \ldots , s_n)\) is the array of the states of components in A, whereas \({\mathbb {E}}= (e_1, \ldots , e_m)\) is the array of events within links in A.Footnote 1 We assume that, sooner or later, A becomes quiescent anew.
The sequence of component transitions moving A from the initial (quiescent) state to the final (quiescent) state is the trajectory of A. Given the initial state \(a_0\) of A, the graph embodying all possible trajectories of A, rooted in \(a_0\), is the behavior space of A, written \({ Bsp }(A)\). A trajectory \(h = [t_1(c_1), t_2(c_2), \ldots , t_q(c_q)]\) in \({ Bsp }(A)\), from initial state \(a_0\) to final state \(a_q\), can be represented as:
where intermediate states \(a_1, a_2, \ldots , a_{q-1}\) of A are indicated.
3 Complex Active Systems
A complex active system \({\mathcal {A}}\) is a hierarchy of interacting active systems \(A_1, \ldots , A_k\). In order to make AS’s interact with one another, four actions are required for each AS A:
-
1.
Definition of a set of input terminals, each one being connected with an input terminal of a component in A;
-
2.
Definition of a set of output terminals;
-
3.
Specification of a set of patterns, with each pattern being a pair \((p(\omega ), r)\), where p is a pattern event, \(\omega \) an output terminal of A, and r a regular expression whose alphabet is a set of component transitions in A.Footnote 2
-
4.
Connection of each output terminal of A with an input terminal of another AS \(A'\).
Given a pattern \((p(\omega ), r)\), pattern event p is generated at output terminal \(\omega \) of A when a subsequence of the trajectory of A matches regular expression r. Since there is a link from output terminal \(\omega \) of A to an input terminal of \(A'\), which is in its turn connected with an input terminal of a component \(c'\) of \(A'\), it follows that the occurrence of p is bound to trigger a transition of \(c'\). This way, the behavior of A is doomed to influence (although not completely determine) the behavior of \(A'\).
Like an active system, a complex active system \({\mathcal {A}}\) can be either quiescent or reacting. \({\mathcal {A}}\) is quiescent when all AS’s in \({\mathcal {A}}\) are quiescent and all generated pattern events (if any) have been consumed. When reacting, the occurrence of an AS transition moves \({\mathcal {A}}\) to a new state. Each state of \({\mathcal {A}}\) is a triple \(({\mathbb {A}}, {\mathbb {E}}, {\mathbb {P}})\), where:
-
\({\mathbb {A}}= (a_1, \ldots , a_n)\) is the array of the states of AS’s in \({\mathcal {A}}\), namely \(A_1, \ldots , A_n\);
-
\({\mathbb {E}}= (e_1, \ldots , e_m)\) is the array of pattern events within links between AS’s in \({\mathcal {A}}\);
-
\({\mathbb {P}}= (p_1, \ldots , p_k)\) is the array of states of pattern-event recognizers.Footnote 3
The sequence of AS transitions moving \({\mathcal {A}}\) from the initial (quiescent) state to the final (quiescent) state is the trajectory of \({\mathcal {A}}\). Given the initial state \(\alpha _0\) of \({\mathcal {A}}\), the graph embodying all possible trajectories of \({\mathcal {A}}\), rooted in \(\alpha _0\), is the behavior space of \({\mathcal {A}}\), written \({ Bsp }({\mathcal {A}})\). A trajectory \(h = [t_1(A_1), t_2(A_2), \ldots , t_q(A_{q-1}), t_q(A_q)]\) in \({ Bsp }({\mathcal {A}})\), from initial state \(\alpha _0\) to final state \(\alpha _q\), can be represented as:
where intermediate states \(\alpha _1, \alpha _2, \ldots , \alpha _{q-1}\) of \({\mathcal {A}}\) are indicated.
Example 2
Displayed in Fig. 3 is a power transmission line. Each side of the line is protected from short circuits by two breakers, namely b and r on the left, and \(b'\) and \(r'\) on the right. Both b and \(b'\) (the primary breakers) are connected to a sensor of voltage. If a short circuit (for instance, a lightning) strikes the line, then each sensor will detect the lowering of the voltage and command the associated breaker to open. If both breakers open, then the line will be isolated, thereby causing the short circuit to vanish. If so, the two breakers are commanded to close in order to restore the line.
However, faulty behavior may occur: either the sensor does not command the breaker to open or the breaker does not open. Such misbehavior is detected by a monitor (one for each side of the line). For example, similarly to the sensor, the monitor on the left-hand side commands the recovery breaker r to open. In doing so, it also informs the monitor on the right-hand side to perform the same action on recovery breaker \(r'\). For safety reasons, once opened, recovery breakers cannot be closed again, thereby leaving the line isolated.
CAS \({\mathcal {L}}\) modeling the protected power transmission line displayed in Fig. 3
The protected line can be modeled as the CAS outlined in Fig. 4, called \({\mathcal {L}}\), which is composed of four AS’s, namely: P (the protection hardware on the left, including sensor s and breaker b), \(P'\) (the protection hardware on the right, including sensor \(s'\) and breaker \(b'\)), M (the monitoring apparatus, including monitors m and \(m'\), and recovery breakers r and \(r'\)), and L (including line l). Arrows within AS’s denote links between components. For instance, P includes a link from s to b, meaning that an event generated by s can be consumed by b.
For the sake of simplicity, we assume that, when an event is already present in a link, no transition generating a new event on the same link can be triggered. Links between m and \(m'\) allow monitors to communicate to one another. Instead, arrows between AS’s denote links aimed at conveying pattern events. For instance, the link from P to M makes pattern events (occurring in P) available to m in M.
Models monitor and line are displayed in Fig. 5. As such, monitor involves input terminals E and I, and output terminals O and R. Terminal E is entered by the link exiting the protection hardware (either P or \(P'\)), conveying the pattern events occurring in the latter. R is linked with the recovery breaker, while O and I are linked with the other monitor. Displayed under the topological models are the behavioral models. Transitions for monitor and line are detailed below (where pattern events are in bold).
-
(Monitor) \(m_1\) consumes \(\mathbf{{nd}}(E)\) and outputs \({ op }(R)\) and \({ rc }(O)\); \(m_2\) consumes \(\mathbf{{nd}}(E)\) and outputs \({ op }(R)\) only; \(m_3\) consumes \({ rc }(I)\) and outputs \({ op }(R)\); \(m_4\) consumes \(\mathbf{{nd}}(E)\); \(m_5\) consumes \(\mathbf{{di}}(E)\); \(m_6\) consumes \(\mathbf{{co}}(E)\); \(m_7\) consumes \(\mathbf{{nc}}(E)\); \(m_8\) consumes \(\mathbf{{di}}(E)\); \(m_9\) consumes \(\mathbf{{co}}(E)\); \(m_{10}\) consumes \(\mathbf{{nc}}(E)\).
-
(Line) \(l_1\), \(l_2\): consume \(\mathbf{{ni}}(E)\); \(l_3\), \(l_4\): consume \(\mathbf{{ni'}}(E')\); \(l_5\), \(l_6\): consume \(\mathbf{{nr}}(E)\); \(l_7\), \(l_8\): consume \(\mathbf{{nr'}}(E')\); \(l_9\), \(l_{10}\): consume \(\mathbf{{ps'}}(E)\); \(l_{11}\), \(l_{12}\): consume \(\mathbf{{ps}}(E')\).
Pattern events have the following meaning. \(\mathbf{{di}}\): the protection hardware disconnects the side of the line; \(\mathbf{{co}}\): the protection hardware connects the side of the line; \(\mathbf{{nd}}\): the protection hardware fails to disconnect the side of the line; \(\mathbf{{nc}}\): the protection hardware fails to connect the side of the line; \(\mathbf{{nr}}\), \(\mathbf{{nr'}}\): the left/right side of the line cannot be reconnected; \(\mathbf{{ni}}\), \(\mathbf{{ni'}}\): the left/right side of the line cannot be isolated; \(\mathbf{{ps'}}\), \(\mathbf{{ps}}\): the short circuit persists on the left/right side of the line.
Patterns for P, \(P'\), and L are listed in Table 1. For example, pattern event \(\mathbf{{nd}}\) occurs either when \(s_3(s)\) (the sensor fails to open the breaker) or \(s_1(s)\, b_3(b)\) (the sensor commands the breaker to open, yet the breaker fails to open). For each pattern \((p(\omega ),r)\) in Table 1, the alphabet of r is defined as follows. For P and \(P'\), the alphabet of r is the whole set of transitions of the involved components (breaker and sensor). For M, the alphabet equals the set of transitions involved in r only.
4 Uncertain Temporal Observations
During its trajectory, a CAS \({\mathcal {A}}\), embodying AS’s \(A_1, \ldots , A_k\), generates a sequence of observable labels, called the trace of the trajectory. Observable labels are generated for observable transitions only. In this respect, the trace is the projection of the trajectory on the labels associated with observable component transitions. Still, what is perceived by the observer, and given in input to the diagnosis engine, is a relaxation of the trace called an uncertain temporal observation. An uncertain temporal observation is an array \(({\mathcal {O}}_1, \ldots , {\mathcal {O}}_k)\), where \({\mathcal {O}}_i\), \(i \in {[1 {\, .. \,}k]}\), is the uncertain temporal observation of \(A_i\). The relaxation of a trace \({\mathcal {T}}= [\ell _1, \ldots , \ell _m ]\) into \({\mathcal {O}}= ({\mathcal {O}}_1, \ldots , {\mathcal {O}}_k)\) is obtained as follows:
-
1.
\({\mathcal {T}}\) is relaxed into an array \({\mathcal {T}}^*= ({\mathcal {T}}_1, \ldots , {\mathcal {T}}_k)\) of sequences, with each \({\mathcal {T}}_i\), \(i \in {[1 {\, .. \,}k]}\), being the subsequence of \({\mathcal {T}}\) involving the labels of \({\mathcal {T}}\) which are associated with transitions of components in \(A_i\);
-
2.
Each \({\mathcal {T}}_i = [\ell ^i_1, \ldots , \ell ^i_{m_i}]\) in \({\mathcal {T}}^*\) is relaxed into a sequence \({\mathcal {L}}_i = [S^i_1, \ldots , S^i_{m_i}]\), where \(S^i_j\), \(j \in {[1 {\, .. \,}m_i]}\), is a set of labels including \(\ell ^i_j\), along with possibly additional spurious labels (possibly including the null \({\varepsilon }\) label), thereby obtaining \({\mathcal {T}}^*_S = [{\mathcal {L}}_1, \ldots , {\mathcal {L}}_k ]\);
-
3.
Additional spurious sets can be inserted into each \({\mathcal {L}}_i\) in \({\mathcal {T}}^*_S\), with each spurious set involving at least two labels, one of which is necessarily \({\varepsilon }\), thereby obtaining \({\mathcal {T}}^*_{\varepsilon }= [{\mathcal {L}}'_1, \ldots , {\mathcal {L}}'_k ]\);
-
4.
Each \({\mathcal {L}}'_i\) in \({\mathcal {T}}^*_{\varepsilon }\) is relaxed into a DAG \({\mathcal {O}}_i\), where sets in \({\mathcal {L}}'_i\) are the nodes of \({\mathcal {O}}_i\), while an arc \({{S^i_p}\rightarrow {S^i_q}}\) is in \({\mathcal {O}}_i\) only if \(S^i_p\) precedes \(S^i_q\) in \({\mathcal {L}}'_i\), thereby obtaining the uncertain temporal observation \({\mathcal {O}}= ({\mathcal {O}}_1, \ldots , {\mathcal {O}}_k)\).
The mode in which a trace is relaxed into an uncertain temporal observation is not under the control of the observer; therefore, the original trace generated by the CAS is, generally speaking, unknown to the observer.
Example 3
Let \({\mathcal {T}}= [{ awk }, { awk' }, { trg }, { opb' }, { opr }]\) be the trace of CAS \({\mathcal {L}}\) (displayed in Fig. 4). Based on the steps above, a relaxation of \({\mathcal {T}}\) into \({\mathcal {O}}\) can be obtained as follows:
-
1.
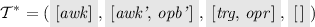 ;
; -
2.
\({\mathcal {T}}^*_S = ([\{{ awk }, { alr }\}], [\{{ awk' }, {\varepsilon }\}, \{{ opb' }\}], [\{{ trg }, { opr }\}, \{{ opr }\}], [\,])\);
-
3.
\({\mathcal {T}}^*_{\varepsilon }= ([\{{ awk }, { alr }\}, \{{ clb }, {\varepsilon }\}], [\{{ awk' }, {\varepsilon }\}, \{{ clb' }, {\varepsilon }\}, \{{ opb' }\}], [\{{ trg }, { opr }\}, \{{ opr }\}], [\,])\);
-
4.
\({\mathcal {O}}= ({\mathcal {O}}_P, {\mathcal {O}}_{P'}, {\mathcal {O}}_M, {\mathcal {O}}_L)\), where the DAG’s representing \({\mathcal {O}}_P\), \({\mathcal {O}}_{P'}\), and \({\mathcal {O}}_M\) are outlined on the left-hand side of Fig. 6, whereas \({\mathcal {O}}_L\) is empty.
Within a DAG \({\mathcal {O}}_A\) representing the uncertain temporal observation of an AS A, the notion of precedence ‘\(\prec \)’ between two nodes is used. This is defined as the smallest relation satisfying the following two conditions (where n, \(n'\), and \(n''\) denote nodes, while \({{n}\rightarrow {n'}}\) denotes an arc from n to \(n'\)): (1) if \({{n}\rightarrow {n'}}\) is an arc then \(n \prec n'\); (2) if \(n \prec n'\) and \(n' \prec n''\) then \(n \prec n''\).
The extension of a node n in \({\mathcal {O}}_A\), denoted \(||n||\), is the set of labels associated with n. A candidate trace \({\mathcal {T}}_\mathrm {c}\) of \({\mathcal {O}}_A\) having set \(N_A\) of nodes, is a sequence of labels so defined:
where nodes n are chosen based on the partial order defined by arcs, while \({\varepsilon }\) labels are removed. The extension of \({\mathcal {O}}_A\) is the set of candidate traces of \({\mathcal {O}}_A\), written \(||{\mathcal {O}}_A||\).
Likewise, the notion of extension can be defined for an uncertain temporal observation \({\mathcal {O}}= ({\mathcal {O}}_1, \ldots , {\mathcal {O}}_k)\) as follows:
It is possible to prove that, for each \({\mathcal {T}}_i\) in array \({\mathcal {T}}^*\), \(i \in {[1 {\, .. \,}k]}\), resulting from the first relaxation step of \({\mathcal {T}}\), we have \({\mathcal {T}}_i \in ||{\mathcal {O}}_i||\). Hence, in virtue of Eq. (2), \({\mathcal {T}}^*\in ||{\mathcal {O}}||\).
Example 4
With reference to Example 3 and the uncertain temporal observations \({\mathcal {O}}_P\), \({\mathcal {O}}_{P'}\), and \({\mathcal {O}}_M\) displayed on the left-hand side of Fig. 6, we have:
-
 ,
, -
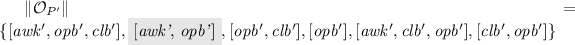 ,
, -
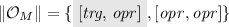 ,
,
where shadowed candidate traces equal the corresponding traces in \({\mathcal {T}}^*\).
In order to match the behavior of the CAS reconstructed by the diagnosis engine against the uncertain temporal observation \({\mathcal {O}}= ({\mathcal {O}}_1, \ldots , {\mathcal {O}}_k)\), each \({\mathcal {O}}_i\), \(i \in {[1 {\, .. \,}k]}\), needs to be somehow indexed. To this end and for efficiency reasons, for each \({\mathcal {O}}_i\), an index space of \({\mathcal {O}}_i\), namely \({ Idx }({\mathcal {O}}_i)\) is generated. This is a deterministic finite automaton (DFA) obtained by determinization of a nondeterministic finite automaton (NFA) called the prefix space of \({\mathcal {O}}_i\), namely \({ Pfx }({\mathcal {O}}_i)\). To define \({ Pfx }({\mathcal {O}}_i)\), we need to define a prefix of \({\mathcal {O}}_i\) and the index of a prefix. A prefix of \({\mathcal {O}}_i\) with set of nodes \(N_i\), is a subset of \(N_i\) defined inductively as follows:
-
1.
The empty set \(\emptyset \) is a prefix of \({\mathcal {O}}_i\);
-
2.
If p is a prefix of \({\mathcal {O}}_i\) and \(n' \in N_i - p\) where \(\forall n \in N_i\) such that \(n \prec n'\) we have \(n \in p\), then \(p \cup \{ n'\}\) is a prefix of \({\mathcal {O}}_i\).
The index of a prefix p, denoted I(p), is the subset of p defined as follows:
Given an index I of p, the set of nodes in p is denoted by \(I^{-1}\). An index I is final when \(I^{-1} = N_i\).
The prefix space of \({\mathcal {O}}_i\) is the NFA \({ Pfx }({\mathcal {O}}_i) = (\varSigma , S, \tau , s_0, S_\mathrm {f})\), where:
-
\(\varSigma \) is the alphabet, which is composed of the labels in \({\mathcal {O}}_i\);
-
S is the set of states, with each state being the index of a prefix of \({\mathcal {O}}_i\);
-
\(s_0 = \emptyset \) is the initial state;
-
\(S_\mathrm {f}\) is the singleton \(\{ s_\mathrm {f} \}\), where \(s_\mathrm {f} \in S, \, I^{-1}(s_\mathrm {f}) = N_i\);
-
\(\tau : S \times \varSigma \mapsto 2^S\) is the nondeterministic transition function, where \({s \xrightarrow {\ell }{s'}} \in \tau \) iff:
$$\begin{aligned} s' = I\left( s \cup \{n\}\right) , \ell \in ||n||, n \in N_i - s, \forall \, {{n'}\rightarrow {n}} \in {\mathcal {O}}_i\, \left( n' \in s\right) . \end{aligned}$$(4)
Example 5
Consider the uncertain temporal observations \({\mathcal {O}}_P\), \({\mathcal {O}}_{P'}\), and \({\mathcal {O}}_M\) displayed on the left-hand side of Fig. 6. The corresponding prefix spaces \({ Pfx }({\mathcal {O}}_P)\), \({ Pfx }({\mathcal {O}}_{P'})\), and \({ Pfx }({\mathcal {O}}_M)\) are outlined in the center, with states being renamed by numbers. Index spaces \({ Idx }({\mathcal {O}}_P)\), \({ Idx }({\mathcal {O}}_{P'})\), and \({ Idx }({\mathcal {O}}_M)\) are shown on the right-hand side of the figure, with states being renamed by symbols \(\mathfrak {I}_i\), \(i \in {[0 {\, .. \,}4]}\).
5 Problem Formulation
Once a real system is modeled as a CAS \({\mathcal {A}}\) composed of AS’s \(A_1, \ldots , A_k\), it can be diagnosed based on the uncertain temporal observation \({\mathcal {O}}= ({\mathcal {O}}_1, \ldots , {\mathcal {O}}_k)\). In this paper we focus on a posteriori diagnosis. That is, we assume that \({\mathcal {O}}\) is relevant to a complete trajectory of \({\mathcal {A}}\), which moves \({\mathcal {A}}\) from the known initial (quiescent) state to an unknown final (quiescent) state.
In order to match \({\mathcal {O}}\) against the behavior of \({\mathcal {A}}\) it is essential to know which are the observable transitions of components and their associated observable labels. This is specified by a viewer of \({\mathcal {A}}\), namely \({\mathcal {V}}= ({\mathcal {V}}_1, \ldots , {\mathcal {V}}_k)\), which is the array of the local viewers of the AS’s, with each local viewer \({\mathcal {V}}_i\), \(i \in {[1 {\, .. \,}k]}\), being a set of pairs \((t, \ell )\), where t is an observable transition of a component in \(A_i\) and \(\ell \) an observable label.
The projection of a trajectory h of \({\mathcal {A}}\) on viewer \({\mathcal {V}}= ({\mathcal {V}}_1, \ldots , {\mathcal {V}}_k)\) is the array of AS traces defined as follows:
We say that trajectory h is consistent with \({\mathcal {O}}\) when \(h_{[{\mathcal {V}}]} \in ||{\mathcal {O}}||\). Generally speaking, \({\mathcal {O}}\) is not sufficient to identify the actual trajectory. Rather, several (possibly an infinite number of) candidate trajectories of \({\mathcal {A}}\) are possibly consistent with \({\mathcal {O}}\).
Similarly to a local viewer which specifies observable transitions, faulty transitions are specified by a local ruler, a set of pairs (t, f), where t is a component faulty transition and f a fault. The array of all local rulers \({\mathcal {R}}_i\), one for each \(A_i\) in \({\mathcal {A}}\), gives rise to the ruler of \({\mathcal {A}}\), namely \({\mathcal {R}}= ({\mathcal {R}}_1, \ldots , {\mathcal {R}}_k)\).
For each candidate trajectory h of \({\mathcal {A}}\), there is a candidate diagnosis of \({\mathcal {A}}\), denoted \(h_{[{\mathcal {R}}]}\), which is the set of faults associated with the faulty transitions within the trajectory:
A diagnosis problem for \({\mathcal {A}}\) is a quadruple:
where \(\alpha _0\) is the initial state of \({\mathcal {A}}\), \({\mathcal {V}}\) a viewer of \({\mathcal {A}}\), \({\mathcal {O}}\) the uncertain temporal observation of \({\mathcal {A}}\), and \({\mathcal {R}}\) a ruler of \({\mathcal {A}}\).
The solution of \({\wp }({\mathcal {A}})\), namely \(\varDelta ({\wp }({\mathcal {A}}))\), is the set of candidate diagnoses \(\delta \) associated with the candidate traces of \({\mathcal {A}}\) that are consistent with \({\mathcal {O}}\):
However, the diagnosis engine is not expected to generate the solution of a diagnosis problem based on Eq. (8). In fact, Eq. (8) relies on \({ Bsp }({\mathcal {A}})\), the behavior space of \({\mathcal {A}}\), whose generation is, generally speaking, practically infeasible. Still, the set of candidate diagnoses generated by the diagnosis engine shall equal \(\varDelta ({\wp }({\mathcal {A}}))\). In other words, the diagnosis technique shall be not only efficient but also sound and complete.
Example 6
With reference to Example 2, we define a diagnosis problem for \({\mathcal {L}}\) as:
where:
-
In initial state \(\lambda _0\), breakers are closed, sensors are idle, and monitors are watch (see component models in Figs. 1 and 5);
-
\({\mathcal {V}}= ({\mathcal {V}}_P, {\mathcal {V}}_{P'}, {\mathcal {V}}_M, {\mathcal {V}}_L)\), where \({\mathcal {V}}_P = \{ (b_1(b), { opb })\), \((b_2(b), { clb })\), \((b_5(b), { alr })\), \((b_6(b), { alr })\), \((s_1(s), { awk })\), \((s_2(s), { ide })\), \((s_3(s), { awk })\), \((s_4(s), { ide })\}\), \({\mathcal {V}}_{P'} = \{ (b_1(b'), { opb' })\), \((b_2(b'), { clb' })\), \((b_5(b'), { alr' })\), \((b_6(b'), { alr' })\), \((s_1(s'), { awk' })\), \((s_2(s'), { ide' })\), \((s_3(s'), { awk' })\), \((s_4(s'), { ide' })\}\), \({\mathcal {V}}_{M} = \{ (m_1(m), { trg })\), \((m_2(m), { trg })\), \((m_3(m), { trg })\), \((b_1(r), { opr })\), \((b_2(r), { clr })\), \((m_1(m'), { trg' })\), \((m_2(m'), { trg' })\), \((m_3(m'), { trg' })\), \((b_1(r'), { opr' })\), \((b_2(r'), { clr' })\}\), and \({\mathcal {V}}_L~=~\emptyset \) (that is, L is unobservable);
-
\({\mathcal {O}}= ({\mathcal {O}}_P, {\mathcal {O}}_{P'}, {\mathcal {O}}_M, {\mathcal {O}}_L)\), where \({\mathcal {O}}_P\), \({\mathcal {O}}_{P'}\), and \({\mathcal {O}}_M\) are displayed on the left-hand side of Fig. 6, whereas \({\mathcal {O}}_L\) is empty (necessarily so, being L unobservable);
-
\({\mathcal {R}}= ({\mathcal {R}}_P, {\mathcal {R}}_{P'}, {\mathcal {R}}_M, {\mathcal {R}}_L)\), where \({\mathcal {R}}_P = \{(b_3(b), { fob })\), \((b_4(b), { fcb })\), \((s_3(s), { fos })\), \((s_4(s), { fcs })\}\), \({\mathcal {R}}_{P'} = \{(b_3(b'), { fob' })\), \((b_4(b'), { fcb' })\), \((s_3(s'), { fos' })\), \((s_4(s'), { fcs' })\}\), \({\mathcal {R}}_M = \{(m_2(m), { fm })\), \((m_2(m'), { fm' })\), \((b_3(r), { for })\), \((b_4(r), { fcr })\), \((b_3(r'), { for' })\), \((b_4(r'), { fcr' })\}\), \({\mathcal {R}}_L = \{(l_1(l), { fls })\), \((l_2(l), { fls })\), \((l_3(l), { fls' })\), \((l_4(l), { fls' })\), \((l_5(l), { fli })\), \((l_6(l), { fli })\), \((l_7(l), { fli' })\), \((l_8(l), { fli' })\), \((l_9(l), { flp }), (l_{10}(l), { flp })\), \((l_{11}(l), { flp' }), (l_{12}(l), { flp' })\}\).
6 Preprocessing
For efficiency reasons, it is convenient to perform some preprocessing on the CAS specification before the diagnosis engine is operating. The extent of such offline preprocessing is varying and depends on the performance requirements of the application domain. In particular, in order to detect pattern events, we need to maintain the recognition states of patterns. Since patterns are described by regular expressions, specific automata-based recognizers are to be generated as follows:
-
1.
For each pattern \((p(\omega ), r)\), a pattern automaton P equivalent to r is generated, with final states marked by \(p(\omega )\);
-
2.
The set \({\mathbf {P}}\) of pattern automata is partitioned based on AS and the alphabet of r;
-
3.
For each part \({\mathbb {P}}= \{ P_1, \ldots , P_h \}\) in \({\mathbf {P}}\), four actions are performed:
-
(3a) A nondeterministic automaton \({\mathcal {N}}\) is created by generating its initial state \(n_0\) and one empty transition from \(n_0\) to each initial state of \(P_i\), \(i \in {[1 {\, .. \,}h]}\);
-
(3b) In each \(P_i\), \(i \in {[1 {\, .. \,}h]}\), an empty transition from each non-initial state to \(n_0\) is inserted (this allows for pattern-matching of overlapping strings of transitions);
-
(3c) \({\mathcal {N}}\) is determinized into \({\mathcal {P}}\), where each final state d is marked by the pattern event that is associated with the states in d that are final in the corresponding pattern automaton (in fact, each state d of the deterministic automaton is identified by a subset of the states of the equivalent nondeterministic automaton; besides, we assume that only one pattern event at a time can be generated);
-
(3d) \({\mathcal {P}}\) is minimized into the pattern space of part \({\mathbb {P}}\).
-
Example 7
Displayed on the left-hand side of Fig. 7 is the nondeterministic automaton \({\mathcal {N}}\) generated in action (3b) for pattern events \(\mathbf{{di}}(O)\), \(\mathbf{{co}}(O)\), \(\mathbf{{nd}}(O)\), and \(\mathbf{{nc}}(O)\). The tabular representation of the resulting pattern space \({\mathcal {P}}_P\) is outlined on the right-hand side. Listed in first column are the states (0 is the initial state), with final states being shaded. For each pair state-transition, the next state is specified. Listed in the last column are the pattern events associated with final states. Pattern space \({\mathcal {P}}_{P'}\) is generated in the same way.
Since regular expressions of pattern events for M are defined on different alphabets, six additional pattern spaces are to be generated: \({\mathcal {P}}_{\mathbf{{nr}}}\), \({\mathcal {P}}_{\mathbf{{ni}}}\), \({\mathcal {P}}_{\mathbf{{ps'}}}\), \({\mathcal {P}}_{\mathbf{{nr'}}}\), \({\mathcal {P}}_{\mathbf{{ni'}}}\), and \({\mathcal {P}}_{\mathbf{{ps}}}\).
7 Problem Solving
Behavior reconstruction in diagnosis of CAS’s avoids materializing the behavior of the CAS, that is, the automaton whose language equals the set of CAS trajectories. Instead, reconstruction is confined to each single AS based on the local observation and the interface constraints on pattern-event occurrences coming from neighboring inferior AS’s within the hierarchy of the CAS.
The essential point is that such pattern events come with diagnosis information from inferior AS’s, which is eventually combined with the diagnosis information of the superior AS, thereby allowing for the sound and complete solution of the diagnosis problem.
Intuitively, the flow of reconstruction in the hierarchy of the CAS is bottom-up. For an AS A with children \(A_1, \ldots , A_k\), the behavior of A, namely \({ Bhv }(A)\), is reconstructed based on the interfaces of the children, namely \({ Int }(A_1), \ldots , { Int }(A_k)\), and the local observation of A, namely \({\mathcal {O}}_A\). The interface is derived from the behavior. Thus, for any AS A, both \({ Bhv }(A)\) and \({ Int }(A)\) are to be generated (with the exception of the root, for which no interface is generated).
As such, the notions of behavior and interface depend on each other. However, such a circularity does not hold for leaf nodes of the CAS (e.g. P and \(P'\) in Fig. 4): given a leaf node A, the behavior \({ Bhv }(A)\) is reconstructed based on \({\mathcal {O}}_A\) only, as no interface constraints exist for A. On the other hand, the behavior of the root node (e.g. L in Fig. 4) needs to be submitted to further decoration-based processing in order to distill the set of candidate diagnoses.
In short, four sorts of graphs are required in reconstruction: unconstrained behavior (for leaf nodes), interface (for non-root nodes), constrained behavior (for non-leaf nodes), and decorated behavior (for root node).
Example 8
With reference to CAS \({\mathcal {L}}\) in Fig. 4 and the diagnosis problem defined in Example 6, namely \({\wp }({\mathcal {L}}) = (\lambda _0, {\mathcal {V}}, {\mathcal {O}}, {\mathcal {R}})\), we first need to generate the unconstrained behavior of AS’s P and \(P'\) based on local observations \({\mathcal {O}}_P\) and \({\mathcal {O}}_{P'}\), respectively.
Displayed in Fig. 8 are the index space, the unconstrained behavior, and the interface relevant to P (left) and \(P'\) (right). Consider the generation of \({ Bhv }(P')\). As detailed in the right-hand side of Table 2, each state is identified by five fields: the state of sensor \(s'\), the state of breaker \(b'\), the event (if any) ready at terminal \(I(b')\), the state of pattern space \({\mathcal {P}}_{P'}\), and the state of the index space \({ Idx }({\mathcal {O}}_{P'})\).
The generation of the behavior starts at the initial state 0 and progressively materializes the transition function by applying triggerable transitions to each state created so far. A state is final when all events are consumed and the state of the index space is final. The transition from 1 to 3 is marked by \(\mathbf{{di'}}(O)\) pattern event as the state of \({\mathcal {P}}_{P'}\) becomes final in 3 (namely, state 1 in the right-hand side of Fig. 7, where \(\mathbf{{di}}(O)\) needs to be replaced by \(\mathbf{{di'}}(O)\)).
In what follows, a diagnosis \(\delta \) is a set of faults. We make use of the join operator between two sets of diagnoses, namely \(\varDelta _1\) and \(\varDelta _2\), defined as follows:
Example 9
Shown on the right of each behavior in Fig. 8 are interfaces \({ Int }(P)\) and \({ Int }(P')\), derived from the corresponding behavior as follows.
-
1.
The identifier of a component transition t(c) marking an arc of the behavior and associated with a pattern event is replaced by:
-
The singleton \(\{ \emptyset \}\), if t(c) is normal;
-
The singleton \(\{\{f\}\}\), if t(c) is faulty, with f being the associated fault.
-
-
2.
Interpreting as \({\varepsilon }\)-transitions those transitions which are not associated with pattern events, the obtained nondeterministic automaton (NFA) is determinized so that each state of the resulting deterministic automaton (DFA) contains the \({\varepsilon }\)-closure in all its structure (rather than the subset of NFA states only, as is in the classical determinization algorithm [9]).
-
3.
Within each state d of the DFA, each NFA state n is marked by the diagnosis set generated by all paths starting at the root state in d and ending at n, while identifiers of component transitions are eventually removed.
-
4.
Let p be the pattern event marking a transition t exiting a state d in the DFA, \(\varDelta _p\) the diagnosis set associated with p in step 1, and \(\varDelta \) the diagnosis set associated with the NFA state in d from which t is derived in the determinization process. \(\varDelta _p\) is replaced by \(\varDelta \bowtie \varDelta _p\).
Example 10
Displayed in Fig. 9 is the constrained behavior \({ Bhv }(M)\), which is generated based on index space \({ Idx }({\mathcal {O}}_M)\). Each state of \({ Bhv }(M)\) includes two sorts of additional information: the pattern events ready (if any) at input terminals of M, and the pair \((i, i')\) of interfaces states relevant to interfaces \({ Int }(P)\) and \({ Int }(P')\), respectively. A final state needs the additional condition that both states in \((i, i')\) are final in the respective interface. When reconstructing a transition triggered by a pattern event, the latter is required to mark a transition exiting the corresponding state in the interface, otherwise the transition cannot be reconstructed.
Compared with Example 9, the derivation of interface \({ Int }(M)\) shown in Fig. 9 exhibits two peculiarities: step 2 creates a DFA state resulting from two NFA transitions, exiting states 6 and 8 respectively, both marked by pair \((b_1(r), \mathbf{{nr}}(O))\), and step 3 shall account for the diagnosis sets associated with pattern events.
Once generated, the behavior shall be decorated by sets of diagnoses associated with states, in a way similar to step 3 in marking NFA states within interface states.
Example 11
Outlined on the right of Fig. 9 is the decorated behavior \({ Bhv }^*(L)\). Starting from the singleton \(\{ \emptyset \}\) marking state 0, the candidate set associated with state 1 is \(\varDelta (1)\) \(=\) \(\{ \emptyset \}\) \(\bowtie \) \(\{\{ { fob }, { fm }\}\}\) \(=\) \(\{\{ { fob }, { fm }\}\}\). Since \(l_5(l)\) is faulty (associated with fault \({ fli }\)), eventually we have \(\varDelta (2) = \varDelta (1) \bowtie \{ \{ { fli }\} \} = \{ \{ { fob }, { fm }, { fli }\} \}\). Hence, the solution of the diagnosis problem \({\wp }({\mathcal {L}})\) defined in Example 6 consists of one single diagnosis involving three faults: breaker b fails to open (\({ fob }\)), monitor m fails to communicate with monitor \(m'\) (\({ fm }\)), and line l is isolated (\({ fli }\)).
8 Conclusion
As shown in [11], despite their complexity, CAS’s can be diagnosed more efficiently than monolithic DES’s, whose diagnosis is affected by exponential complexity (in the number of components), either offline when generating the diagnoser [20, 21], or online when reconstructing the system behavior [1, 13]. Specifically, in [11], complexity (in time and space) is shown to be linear with the number of components within the CAS.
The contribution of this paper is to extend diagnosis of CAS’s introduced in [11] by means of uncertain temporal observations. Unlike a (certain) temporal observation, which consists of a sequence of totally ordered observable labels, within an uncertain observation, observable labels are both uncertain and partially ordered. Despite this dissimilarity, an uncertain temporal observation can be thought of as a set of candidate temporal observations. The notion of index space allows the diagnosis engine to account for all candidate temporal observations by means of a scalar value, the observation index \(\mathfrak {I}\), which is a surrogate of an integer indexing a temporal observation within states of the reconstructed behavior. In other words, when uncertain temporal observations are considered, the integer is replaced by a scalar value \(\mathfrak {I}\) identifying a state of the index space. Consequently, neither space nor time complexity is expected to deteriorate when uncertain temporal observations come into play in diagnosis of CAS’s.
Despite being introduced based on a simple reference example, diagnosis of CAS’s is a general technique which can be applied to any real system that can be conveniently modeled as a CAS, in terms of interconnected AS’s and relevant pattern events.
Diagnosis of CAS’s is still in its infancy. Further research is expected in several directions. Offline preprocessing can be performed in order to accelerate the online diagnosis engine by generating in a suitable form the behavior space of each AS embedded in the CAS. Also, monitoring-based diagnosis can be envisioned, where the diagnosis engine does not operate a posteriori but, rather, it reacts to each fragment of available observation by providing the diagnosis information relevant to such a fragment only.
Notes
- 1.
We assume that at most one event can be stored in a link. If the link is empty (no stored event), the corresponding value in array \({\mathbb {E}}\) is denoted \({\varepsilon }\) (empty event).
- 2.
We assume the classical operators for regular expressions, namely concatenation, disjunction, optionality, and repetition. If necessary, additional more specific operators can be involved.
- 3.
As detailed in Sect. 6, the need for pattern matching of (possibly overlapping) pattern events against relevant regular expressions requires the (offline) generation of specific recognizers, these being DFA’s named pattern spaces.
References
Baroni, P., Lamperti, G., Pogliano, P., Zanella, M.: Diagnosis of large active systems. Artif. Intell. 110(1), 135–183 (1999)
Bossomaier, T., Green, D.: Complex Systems. Cambridge University Press, Cambridge (2007)
Brand, D., Zafiropulo, P.: On communicating finite-state machines. J. ACM 30(2), 323–342 (1983)
Cassandras, C., Lafortune, S.: Introduction to Discrete Event Systems. The Kluwer International Series in Discrete Event Dynamic Systems, vol. 11. Kluwer Academic Publishers, Boston (1999)
Christensen, H., Kruijff, G., Wyatt, J. (eds.): Cognitive Systems. Springer, Berlin (2010)
Chu, D.: Complexity: against systems. Theor. Biosci. 130(3), 229–245 (2011)
Gell-Mann, M.: What is complexity? In: Curzio, A.Q., Fortis, M. (eds.) Complexity and Industrial Clusters, pp. 13–24. Springer, Heidelberg (2002)
Goles, E., Martinez, S.: Complex Systems. Springer, Heidelberg (2014)
Hopcroft, J., Motwani, R., Ullman, J.: Introduction to Automata Theory, Languages, and Computation, 3rd edn. Addison-Wesley, Reading (2006)
Kaneko, K., Tsuda, I.: Complex Systems: Chaos and Beyond: A Constructive Approach with Applications in Life. Springer, Heidelberg (2013)
Lamperti, G., Quarenghi, G.: Intelligent monitoring of complex discrete-event systems. In: Czarnowski, I., Caballero, A., Howlett, R., Jain, L. (eds.) Intelligent Decision Technologies 2016. Smart Innovation, Systems and Technologies, vol. 56, pp. 215–229. Springer International Publishing, Switzerland (2016)
Lamperti, G., Zanella, M.: Diagnosis of discrete-event systems from uncertain temporal observations. Artif. Intell. 137(1–2), 91–163 (2002)
Lamperti, G., Zanella, M.: Diagnosis of Active Systems - Principles and Techniques. The Springer International Series in Engineering and Computer Science, vol. 741. Springer, Dordrecht (2003)
Lamperti, G., Zanella, M.: Context-sensitive diagnosis of discrete-event systems. In: Walsh, T. (ed.) Twenty-Second International Joint Conference on Artificial Intelligence IJCAI 2011, vol. 2, pp. 969–975. AAAI Press, Barcelona (2011)
Lamperti, G., Zanella, M.: Monitoring of active systems with stratified uncertain observations. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 41(2), 356–369 (2011)
Lamperti, G., Zhao, X.: Diagnosis of higher-order discrete-event systems. In: Cuzzocrea, A., Kittl, C., Simos, D.E., Weippl, E., Xu, L. (eds.) CD-ARES 2013. LNCS, vol. 8127, pp. 162–177. Springer, Heidelberg (2013)
Lamperti, G., Zhao, X.: Specification and model-based diagnosis of higher-order discreteevent systems. In: IEEE International Conference on Systems, Man, and Cybernetics – SMC 2013, Manchester, United Kingdom, pp. 2342–2347 (2013)
Lamperti, G., Zhao, X.: Diagnosis of active systems by semantic patterns. IEEE Trans. Syst. Man Cybern. Syst. 44(8), 1028–1043 (2014)
Licata, I., Sakaji, A.: Physics of Emergence and Organization. World Scientific, Singapore (2008)
Sampath, M., Lafortune, S., Teneketzis, D.: Active diagnosis of discrete-event systems. IEEE Trans. Autom. Control 43(7), 908–929 (1998)
Sampath, M., Sengupta, R., Lafortune, S., Sinnamohideen, K., Teneketzis, D.: Diagnosability of discrete-event systems. IEEE Trans. Autom. Control 40(9), 1555–1575 (1995)
Sibani, P., Jensen, H.: Stochastic Dynamics of Complex Systems, Complexity Science, vol. 2. World Scientific, Singapore (2013)
Vernon, D.: Artificial Cognitive Systems: A Primer. MIT Press, Cambridge (2014)
Woods, D., Hollnagel, E.: Joint Cognitive Systems: Patterns in Cognitive Systems Engineering. CRC Press, Boca Raton (2006)
Acknowledgment
This work was supported in part by Zhejiang Provincial Natural Science Foundation of China (No. LY16F020004), and National Natural Science Foundation of China (No. 61003101).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 IFIP International Federation for Information Processing
About this paper
Cite this paper
Lamperti, G., Zhao, X. (2016). Diagnosis of Complex Active Systems with Uncertain Temporal Observations. In: Buccafurri, F., Holzinger, A., Kieseberg, P., Tjoa, A., Weippl, E. (eds) Availability, Reliability, and Security in Information Systems. CD-ARES 2016. Lecture Notes in Computer Science(), vol 9817. Springer, Cham. https://doi.org/10.1007/978-3-319-45507-5_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-45507-5_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-45506-8
Online ISBN: 978-3-319-45507-5
eBook Packages: Computer ScienceComputer Science (R0)







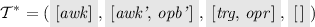 ;
;
 ,
,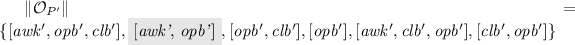 ,
,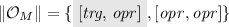 ,
,

