Fast Branch and Bound Algorithm for the Travelling Salesman Problem

Abstract

New strategies are proposed for implementing algorithms based on Branch and Bound scheme. Those include two minimal spanning tree lower bound modifications, a design based on the fact that edges in the optimal tour can never cross in the euclidean TSP and parallelization of Branch and Bound scheme. Proposed approaches are compared with primary algorithms.

1 Introduction

Branch and Bound (Branch and Bound, BnB, branch & bound) is an approach advised for designing exact algorithms solving $\mathcal {NP}$-hard combinatorial optimization and discrete problems. Branch and Bound was introduced by Land and Doig in 1960 [10]. Until the late 1970s, it was the state-of-the-art method for almost all big and complex problems that could not be solved by other techniques known at that time. And it is still used everywhere, where small improvement of solution leads to big rise in profits. Branch and Bound uses a tree search strategy to implicitly enumerate all possible solutions to a given problem, applying pruning rules to eliminate regions of the search space that cannot lead to a better solution [11].

In this article we are considering a minimization problem and the whole used terminology relates to it. In order to optimally solve the problem, Branch and Bound algorithm divides the whole set of solutions $\mathcal {X}$ into mutually exclusive and exhaustive subsets $\mathcal {X}_j$, where $j \in \mathcal {S} = \lbrace 1, 2, 3, \ldots , s \rbrace$. In every moment of its work, algorithm stores the best found solution so far $x_{\mathrm {ub}}$ and its value called upper bound and the set of subsets not yet analysed. Branch and Bound does not search these subsets to which it is assured that they do not contain optimal solution $x^*$, so it is much more effective than an exhaustive search. Decision, if some subset should be analysed or not, is based on its bound and objective function value counted for currently best found solution $K(x_\mathrm {ub})$. For minimization problem, such bound is called lower bound and it is lower or equal to all objective function values evaluated for every element of related subset. It is marked as LB. If for a certain subset, the lower bound is equal or greater than the value of the best solution found so far, such subset is removed from the set of subsets not yet analysed and will be no more considered. A good lower bound is a basic requirement for an efficient Branch and Bound minimization procedure [12].

The idea of Travelling Salesman Problem, TSP for short, relies in visiting every city by the sale representative from the given set of n cities exactly once [9], starting from and returning to the home city. In this article we are considering a symmetric TSP, where the distance between two cities is the same in each opposite direction. We also assume that there is a direct connection from each node to every other one. Formally, this problem is described as a search for the shortest Hamiltonian cycle [7] in the complete and symmetric graph $\mathcal {K}_n = (\mathcal {V}_n, \mathcal {E}_n)$ containing $n = |\mathcal {V}_n|$ nodes and $m = |\mathcal {E}_n| = {{n}\atopwithdelims (){2}}$ edges. Nodes are numbered from 1 to n. We assume without loss of generality that the home city is the node with index number 1. Edge e, which connects nodes i and j, is marked as $\lbrace i,j \rbrace$ or $\lbrace j, i \rbrace$ and their distances are stored in the distance matrix $D_n$.

Branch and Bound algorithm for TSP constructs solutions by visiting cities. On each step there may be more than one remaining city to visit. The process of constructing solutions can be presented as a decision tree. Each node in such tree refers to a subset of the solution set and a lower bound can be established for it. Branch and Bound algorithm creates solutions by exploring such tree. It will not visit these nodes of the decision tree, for which it has certainty that it will not lead to the optimal solution.

The role of parallel algorithms in solving NP-hard problems significantly increased in the last decade. Bożejko proposed an improvement for speeding up the process of solving a single machine scheduling problem with total tardiness cost function by parallelization of generation of paths [2], a parallel genetic algorithm for the flow shop scheduling problem [4] and a method for solving permutational routing problems by population-based metaheuristics [5]. The same author designed new parallel objective function determination methods for the job shop scheduling [3] and flow shop [1] problems. Jagiełło and Żelazny proposed a parallel cost function approach for the Distance Constrained Vehicle Routing Problem which was designed to work on Graphics Processing Units (GPUs) [8]. In this paper we propose a parallel Branch and Bound design for the TSP problem.

2 Lower Bounds

The lower bound $LB(\mathcal {X}_j)$ for a given node in the decision tree (that reflects to a certain set of solutions $\mathcal {X}_j$) is evaluated as a sum of the travelled distance $MIL(\mathcal {X}_j)$ and the lower estimation of the remaining distance $LE(\mathcal {X}_j)$,

$$\begin{aligned} LB(\mathcal {X}_j) = MIL(\mathcal {X}_j) + LE(\mathcal {X}_j). \end{aligned}$$

(1)

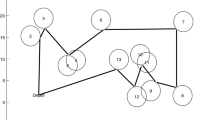
It should be noted, when the travelling salesman visited k cities, the remaining way is a Hamiltonian path starting from the last visited city, that visits every city not visited so far and returning to the home city. It is showed in Fig. 1.

Fig. 1.

Searched Hamiltonian cycle. The tour that has to be passed is marked by the dashed line.

The lower estimation estimates from the bottom an overall length of such shortest Hamiltonian path. This path is described by the following properties:

• (a) it does not visit already visited k nodes,

• (b) each node of the considered graph is visited only once,

• (c) there exists a subpath linking every two nodes of the considered graph,

• (d) it assumes beginning and ending node,

• (e) if the number of not visited cities is greater than one and travelling salesman is not currently in the home city, he cannot directly pass the way from the current city to some not visited city and immediately return to the home city,

• (f) it is built from $n-k+1$ edges,

• (g) the first and the last city of the Hamiltonian path are connected with only one city.

By the relaxation of above constraints, we get lower estimation of the remaining distance $LE(\mathcal {X}_j)$. The weaker relaxation, the greater value of the lower estimation and it leads to better lower estimation (that rejects more solutions).

The Total Length of the Shortest Feasible Connections. The weakest and the most simple lower estimation LE of the remaining distance is obtained by counting the total length of the shortest not visited edges. It satisfies the constraints (a) and (b). Relaxation of constraints involves removal of constraints (b), (c), (d), (e), (f) and (g).

In order to evaluate the lower estimation, the distances associated with the inaccessible connections are removed from the weight matrix. Firstly, zeros from the main diagonal are removed. If the travelling salesman comes out from the city i, the numbers in the row with index i should be removed from the weight matrix. Afterwards, if travelling salesman enters the city with index j and it is not a home city, then from the weight matrix, values from the column j are removed. Moreover, if city with index j is not a second last one (such city, after which travelling salesman returns to the home city), value $d_{j1}$ must be removed from the weight matrix. We determine the number of the remaining connections r that have to be passed as

$$\begin{aligned} r = n - k + 1, \end{aligned}$$

(2)

where n is the number of all cities and k is the number of visited cities.

Values that were not removed from the weight matrix are sorted in the non-decreasing order and form a finite sequence $(a_n)$. The sum of the first r values is the lower estimation of the remaining distance. Then, the lower bound can be computed from (1).

The Weight of the Minimum Spanning Tree. In this case, the lower estimation of the remaining distance LE and the lower bound is equal to the weight of the minimum spanning tree for the complete sub-graph that consists of the city where actually the travelling salesman is located $x_k$, not having visited cities so far $\left\{ x_{k+1}, x_{k+2}, x_{k+3}, \ldots , x_n \right\}$ and the home city $x_1 = 1$. It satisfies the constraints (a), (c) and (f). Relaxation involves removal of the constraints (b), (d), (e) and (g). In order to evaluate the minimum spanning tree weight, Prim’s algorithm is used. When the weight of the minimum spanning tree is computed (and it is also a value of the lower estimation LE), (1) will be used to determine the lower bound.

The Weight of the Minimum Spanning Tree – 1st Modification. Algorithm was proposed by Mariusz Makuchowski from Department of Control Systems and Mechatronics of Wrocław University of Science and Technology (personal communication, November 3, 2014). The lower estimation of the remaining distance is evaluated as a sum of minimum spanning tree weight for graph consisting of the cities not having been visited so far $\left\{ x_{k+1}, x_{k+2}, x_{k+3}, \ldots , x_n \right\}$ and the home city $x_1 = 1$ and the sum of weights of two shortest edges connecting the home city with nearest not visited edge and the current city with nearest not visited edge. If travelling salesman is currently in the home city, lower estimation is counted as a sum of the weight of minimal spanning tree in the graph containing not visited cities and doubled distance from the home city to the nearest not visited node. It satisfies the constraints (a), (c), (f) and (g). Relaxation involves removal of the constraints (b), (d) and (e).

The Weight of the Minimum Spanning Tree – 2nd Modification. It is the improved version of the previous algorithm. The lower estimation of the remaining distance is evaluated as a sum of minimum spanning tree weight for graph consisting of not visited cities $\left\{ x_{k+1}, x_{k+2}, x_{k+3}, \ldots , x_n \right\}$ and the sum of two weights of edges connecting the home city and the current city with not visited cities (and these cities must be different). If the travelling salesman is currently in the home city, the lower estimation is a sum of weight of the minimum spanning tree in graph containing not visited cities and the sum of two weights of shortest edges connecting home city with different not visited cities so far. It satisfies constraints (a), (c), (e), (f) and (g). Relaxation involves removal of constraints (b) and (d).

3 Priority of Analysed Sets

The order in which the algorithm searches the decision tree is very important. The size of the priority queue will grow fast if leaves are rarely visited and new upper bounds will not be found. The algorithm must have a tendency to search the graph towards leaves. By assigning a priority to sets stored in the priority queue we control the way the algorithm will search the decision tree.

We chose the following way of counting priority that promotes subsets with the lowest increase of lower bound

$$\begin{aligned} P=\frac{1}{AI}, \end{aligned}$$

(3)

$$\begin{aligned} AI=\frac{LB}{k}. \end{aligned}$$

(4)

where P, AI, LB and k denote the subsets priority in the queue, the mean increase of the lower bound, the lower bound and the number of visited cities accordingly.

4 Parallel Branch and Bound Algorithm

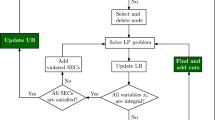
In the parallel algorithm we use a pool approach with arbitrary fixed number of processes. It means that program executes in several processes and one of them will be called supervisory process and the rest will be called worker processes (see Fig. 2). In the initialization phase, supervisory process reads the instance data from the TSPLIB file, generates the weight matrix and distributes it to all worker processes. It also establishes the best solution found so far and the upper bound by running 2-opt algorithm on the result of the nearest neighbour algorithm. It stores the priority queue of solution sets not analysed so far and the best solution so far.

During computation phase, if some worker process notifies the supervisory process about its idle state via WORKER_FINISHED_TASK message and if there are still some solutions sets to be analysed in the priority queue, the supervisory process pops the first solution set with the highest priority and sends it to the worker process via PERFORM_TASK_REQ message and stores the information that the process is performing task. Algorithm stops when there are no more sets in the priority queue to analyse and if all worker processes informed supervisory process that they finished analysing task by sending WORKER_FINISHED_TASK.

Each worker process stores the upper bound value. If some worker process found a solution with the objective function value smaller than the upper bound, it sends this solution with upper bound update proposal to the supervisory process in UPPER_BOUND message. The supervisory process checks if the proposed upper bound value is better than the currently stored one. If it is true, the new best solution so far and the new upper bound value are stored in the supervisory process, the new upper bound value is distributed to all worker processes in the UPPER_BOUND message except one which found it and all subsets with the lower bound greater than the new upper bound are removed from the priority queue. Otherwise, the new proposed upper bound value is discarded. Such check is important in a situation when two workers find better solutions (with different objective function values) than the best solution found so far and simultaneously send proposal to the supervisory process for changing the best solution found so far and the upper bound. If the supervisory process obtains upper bound with smaller value first, it will update upper bound and when it obtains one with greater value, second upper bound value change proposal will be discarded after the check.

Fig. 2.

Sequence diagram that describes solving TSP by the Parallel Branch and Bound algorithm. The initialization part of algorithm was omitted.

Worker processes divide set obtained in the PERFORM_TASK_REQ message into subsets. If the subset has only one element it means that the worker found a solution. Otherwise, if obtained subsets contains more than one element, it calculates lower bounds for them. On the basis of the lower bound and the upper bound it is established if the optimal solution can belong to the obtained subset. If it is true, the subset is send back to the supervisory process via TASK_PUSH_REQ.

5 Intersections in Euclidean TSP

The edges in an optimal tour can never cross in an euclidean TSP. If edges $\lbrace i,k \rbrace$ and $\lbrace j,l \rbrace$ did cross, they would constitute the diagonals of a quadrilateral $\lbrace i,j,k,l \rbrace$ and could profitably be replaced by a pair of opposite sides [6]. Instances for which all points are located on the same line are the only exceptions. Based on that fact two algorithms were proposed. The first one is a modification of the Brute force method the second is an adjustment of the Branch and Bound (Branch and Cut) approach. Before adding an edge to the current sub-tour it is probed for crossings with any of the edges of the current sub-tour. If an intersection occurs, the edge will not be added, thus the whole branch will be omitted.

Fig. 3.

Execution time for random data ($log_{10}$ scale)

6 Computational Experiments

The experiments were performed on a machine equipped with an Intel X980 CPU (6 physical cores), 24 GB of RAM, GCC version 4.6.3 (Ubuntu/Linaro 4.6.3-1ubuntu5) and MPICH 1.4.1 (mpic++, mpirun). The execution time of the specified approaches was measured. The sequential algorithms put under test were:

• Branch and Bound (Branch and Cut) with four different lower bound approaches and without and with intersection checking:

  • the shortest feasible connections (BB(sfc), BB(sfc,i)),

  • the minimum spanning tree (BB(mst), BB(mst,i)),

  • the minimum spanning tree – 1st modification (BB(mstm), BB(mstm,i)),

  • the minimum spanning tree – 2nd modification (BB(mstg), BB(mstg,i)).

• Bellman-Held-Karp dynamic algorithm (Bellman),

• Brute force without and with intersections checking (BF, BF(i)).

For the reason that the algorithms were compared with Brute force method only small problem instances were used. TSPLIB contained only two benchmarks, which fulfilled this requirement: burma14 and ulysses16. The results obtained from working with those data sets are presented in Table 1.

Table 1. Execution time for selected benchmarks

It is quite interesting that the dynamic programming design performed so well as it performed best out of all algorithms for the ulysses16 data set. A single case is unfortunately not enough for accurate conclusions. Due to the small number of available benchmarks 7 random instances of sizes from 10 to 17 were generated. Function rand (stdlib) initialized with the seed 734834 was used to obtain x,y values from the range from 0 to 100. The results were presented in Table 2 and in Fig. 3.

Table 2. Execution time for random data

The BF method was not tested against the rand17 instance for the reason that the experiment would take too long (estimated 22 days). The results clearly indicate that the BF and BB algorithms benefit from checking intersections. The modified BB method was vastly faster than its basic version for each lower estimation. Even the BF(i) method has been proved to be working faster than the BB(sfc) algorithm. Both mst lower bound adjustments (1-Makuchowski, 2-Grymin) proved to be superior compared to the standard approach. As expected the dynamic programming technique operated faster than BB(sfc), BB(sfc,i), BF and BB(i) but slower than mst based BB designs (rand10 is the only exception). The BB(mstg,i) method turned out to be the leading solution resulting in shortest execution times for each test instance. Instance size dependent speedup obtained in comparison to the BF, Bellman and BB(mst) algorithms is presented in Fig. 4.

Fig. 4.

BB(mstg,i) speedup compared to selected algorithms for the burma14 benchmark ($log_{10}$ scale)

Table 3. Parallel BB(mstg,i)

Fig. 5.

BB(mstg,i) speedup compared to selected algorithms ($log_{10}$ scale)

Parallel version of the leading approach was tested with the number of mpi processes in the range 2–12 and with the burma14 benchmark. The results were presented in Table 3. It is shown that the mpi implementation utilizes all physical cores. Speedup is rising until the number of mpi processes equals 7 (1 supervisory process and 6 worker processes). MPI processes count dependent speedup calculated in comparison to the sequential versions of the BF, Bellman and BB(mst) algorithms is presented in Fig. 5. The maximum obtained speedup in comparison to the selected approaches is 38.318, 20.545 and 22755.273 accordingly.

7 Conclusion

Both proposed minimal spanning tree modifications proved to perform greatly faster than the base version. The intersections checking approach was successfully combined with Branch And Bound and Brute force designs and provided additional improvements. The Branch and Bound used with 2nd minimum spanning tree modification as lower estimation algorithm and combined with intersections checking mechanism turned out to be the best solution and achieved a massive speedup when compared to the Brute force, Bellman, and Branch and Bound used with standard minimal spanning tree algorithms. Additionally, its parallel version appeared to scale well and provided a further rise in performance.