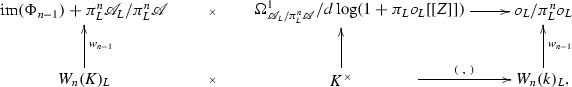Skip to main content
SpringerLink
Log in

Coates–Wiles Homomorphisms and Iwasawa Cohomology for Lubin–Tate Extensions

  • Conference paper
  • First Online:
Elliptic Curves, Modular Forms and Iwasawa Theory (JHC70 2015)

Part of the book series: Springer Proceedings in Mathematics & Statistics ((PROMS,volume 188))

Abstract

For the p-cyclotomic tower of \(\mathbb {Q}_p\) Fontaine established a description of local Iwasawa cohomology with coefficients in a local Galois representation V in terms of the \(\psi \)-operator acting on the attached etale \((\varphi ,\Gamma )\)-module D(V). In this chapter we generalize Fontaine’s result to the case of arbitrary Lubin–Tate towers \(L_\infty \) over finite extensions L of \(\mathbb {Q}_p\) by using the Kisin–Ren/Fontaine equivalence of categories between Galois representations and \((\varphi _L,\Gamma _L)\)-modules and extending parts of [20, 33]. Moreover, we prove a kind of explicit reciprocity law which calculates the Kummer map over \(L_\infty \) for the multiplicative group twisted with the dual of the Tate module T of the Lubin–Tate formal group in terms of Coleman power series and the attached \((\varphi _L,\Gamma _L)\)-module. The proof is based on a generalized Schmid–Witt residue formula. Finally, we extend the explicit reciprocity law of Bloch and Kato [3] Theorem 2.1 to our situation expressing the Bloch–Kato exponential map for \(L(\chi _{LT}^r)\) in terms of generalized Coates–Wiles homomorphisms, where the Lubin–Tate character \(\chi _{LT}\) describes the Galois action on T.

To John Coates on the occasion of his 70th birthday.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 149.00
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 199.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info
Hardcover Book
USD 199.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

  1. 1.

    Note that, for any finite extension K / L contained in \(L_\infty \) the definition \(H^*_{\mathrm {Iw}}(L_\infty /K,V) := \varprojlim _{K \subseteq K' \subseteq L_\infty } H^*(K',V)\) produces the same \(o_L\)-modules. Our notation indicates that we always consider these groups as \(\Gamma _L\)-modules.

  2. 2.

    Another alternative formulation for the definition of \((\; ,\; )\) goes as follows: The residue pairing

    $$\begin{aligned} \mathrm {Res} : \mathscr {A}_L/\pi _L^n\mathscr {A}\times \Omega ^1_{\mathscr {A}_L/\pi _L^n\mathscr {A}}&\longrightarrow o_L/\pi _L^no_L \end{aligned}$$

    induces the pairing

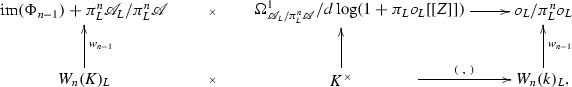
    where the middle vertical map is induced by \(d\log \) and the inverse of the isomorphism \(o_L((Z))^\times /(1+\pi _Lo_L[[Z]])\cong K^\times \).

  3. 3.

    Setting \(L^r_{adm} := L \cap (\pi _L^{-r}\phi _q-1)(\,Fil^rB_{max,L}^+ )\) we still may define

    $$\begin{aligned} L^r_{adm} \xrightarrow {\partial ^r} H^1(L, L t_L^r) \end{aligned}$$

    without knowing the right hand surjectivity in Lemma 8.2.i and define \(\partial ^r\) with source \(L^r_{adm}\) instead. In the course of the next Proposition one can then shown that \(L^r_{adm} = L\).

  4. 4.

    For \(m>0\) one can extend the definition to \(\varprojlim _n L_n^\times \) while for \(m=0\) one cannot evaluate at \(\eta _0=0\)!

  5. 5.

    This power series has a constant term: see [16] for a technical solution.

  6. 6.

    It follows from [12, Proposition III.3.1] that this sequence splits in the category of topological \(\mathbf {Q}_p\)-vector spaces. Since the p-adic topology on \(\mathbf {Q}_p\) coincides with the induced topology from \(B_{max,\mathbf {Q}_p}\) the existence of the transition map is granted by [30, Lem. 2.7.2].

  7. 7.

    Analogous arguments as in Footnote 6 grant the existence of this connecting homomorphism.

  8. 8.

    Using the facts from Footnote 6 one checks that this sequence again satisfies the conditions of [30, Lem. 2.7.2] whence the existence of the long exact cohomology sequence below is granted.

References

  1. Benois, D.: On Iwasawa theory of crystalline representations. Duke Math. J. 104, 211–267 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  2. Bentzen, S., Madsen, I.: Trace maps in algebraic K-theory and the Coates-Wiles homomorphism. J. Reine Angew. Math. 411, 171–195 (1990)

    MathSciNet  MATH  Google Scholar 

  3. Bloch, S., Kato, K.: \(L\)-functions and Tamagawa numbers of motives. In: The Grothendieck Festschrift, vol. I, 333–400, Progress Math., 86, Birkhäuser Boston (1990)

    Google Scholar 

  4. Bourbaki, N.: Topologie Générale. Chaps. 1–10. Springer (2007)

    Google Scholar 

  5. Cherbonnier, F., Colmez, P.: Théorie d’Iwasawa des représentations \(p\)-adiques d’un corps local. J. AMS 12, 241–268 (1999)

    MATH  Google Scholar 

  6. Coates J., Sujatha, R.: Cyclotomic fields and zeta values. Springer (2006)

    Google Scholar 

  7. Coates, J., Wiles, A.: On \(p\)-adic \(L\)-functions and elliptic units. J. Austral. Math. Soc. Ser. A 26(1), 1–25 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  8. Coleman, R.: Division values in local fields. Invent. math. 53, 91–116 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  9. Colmez, P.: Espaces de Banach de dimension finie. J. Inst. Math. Jussieu 1, 331–439 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  10. Colmez, P.: Fontaine’s rings and \(p\)-adic \(L\)-functions. Lecture Notes at Tsinghua Univ. (2004)

    Google Scholar 

  11. Colmez, P.: \((\varphi ,\Gamma )\)-modules et représentations du mirabolique de \({{\rm {GL}}_2}(\mathbb{Q}_p)\). In: Berger, L., Breuil, C., Colmez, P. (eds.) Représentations \(p\)-adiques de groupes \(p\)-adiques, vol. II. Astérisque 330, 61–153 (2010)

    Google Scholar 

  12. Colmez, P.: Théorie d’Iwasawa des représentations de de Rham d’un corps local. Ann. Math. 148(2), 485–571 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  13. Colmez, P.: A generalization of Coleman’s isomorphism. In: Algebraic Number Theory and Related Topics (Kyoto, 1997). Srikaisekikenkysho kkyroku 1026, 110–112 (1998)

    Google Scholar 

  14. de Shalit, E.: The explicit reciprocity law of Bloch–Kato. Columbia University Number Theory Seminar (New York, 1992). Astérisque 228(4), 197–221 (1995)

    Google Scholar 

  15. Fontaine, J.-M.: Répresentations \(p\)-adiques des corps locaux. In: The Grothendieck Festschrift, vol. II, 249–309, Birkhäuser (1990)

    Google Scholar 

  16. Fontaine, J.-M.: Appendice: Sur un théorème de Bloch et Kato (lettre à B. Perrin-Riou). Invent. Math. 115, 151–161 (1994)

    Article  MathSciNet  Google Scholar 

  17. Fourquaux, L., Xie, B.: Triangulable \(O_F\)-analytic \((\varphi _q,\Gamma )\)-modules of rank \(2\). Algebra Number Theory 7(10), 2545–2592 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  18. Fukaya, T., Kato, K.: A formulation of conjectures on \(p\)-adic zeta functions in non-commutative Iwasawa theory. In: Proceedings of St. Petersburg Math. Soc., vol. XII, AMS Transl. Ser. 2, vol. 219, 1–86 (2006)

    Google Scholar 

  19. Hazewinkel, M.: Formal Groups and Applications. Academic Press (1978)

    Google Scholar 

  20. Herr, L.: Sur la cohomologie galoisienne des corps \(p\)-adiques. Bull. Soc. Math. France 126, 563–600 (1998)

    MathSciNet  Google Scholar 

  21. Hewitt, E., Ross, K.: Abstract Harmonic Analysis, vol. I. Springer (1994)

    Google Scholar 

  22. Jensen, C.U.: Les Foncteurs Dérivés de \(\varprojlim \) et leurs Applications en Théorie des Modules. Springer Lect. Notes Math., vol. 254 (1972)

    Google Scholar 

  23. Kato, K.: Lectures on the approach to Iwasawa theory for Hasse-Weil \(L\)-functions via \(B_{\rm {dR}}\). I. Arithmetic algebraic geometry (Trento, 1991), Springer. Lect. Notes Math. 1553, 50–163 (1993)

    Google Scholar 

  24. Kisin, M., Ren, W.: Galois representations and Lubin-Tate groups. Documenta Math. 14, 441–461 (2009)

    MathSciNet  MATH  Google Scholar 

  25. Kölcze P.: Ein Analogon zum Hilbertsymbol für algebraische Funktionen und Witt-Vektoren solcher Funktionen. Diplomarbeit (Betreuer: J. Neukirch) Universität Regensburg (1990)

    Google Scholar 

  26. Lang, S.: Cyclotomic Fields. Springer (1978)

    Google Scholar 

  27. Laubie, F.: Extensions de Lie et groupes d’automorphismes de corps locaux. Compositio Math. 67, 165–189 (1988)

    MathSciNet  Google Scholar 

  28. Lazard, M.: Groupes analytiques \(p\)-adiques. Publ. Math. IHES 26, 389–603 (1965)

    MathSciNet  MATH  Google Scholar 

  29. Michael, E.: Continuous selections II. Ann. Math. 64, 562–580 (1956)

    Article  MathSciNet  MATH  Google Scholar 

  30. Neukirch, J., Schmidt, A., Wingberg, K.: Cohomology of Number Fields. 2nd edn. Springer (2008)

    Google Scholar 

  31. Schneider, P.: Galois representations and \((\varphi ,\Gamma )\)-modules. Lecture Notes, Münster (2015). http://wwwmath.uni-muenster.de/u/schneider/publ/lectnotes/index.html

  32. Schneider, P., Vigneras, M.-F.: A functor from smooth \(o\)-torsion representations to \((\varphi ,\Gamma )\)-modules. In: Arthur, Cogdell, ... (eds.) On Certain L-Functions. Clay Math. Proc., vol. 13, 525–601, AMS-CMI (2011)

    Google Scholar 

  33. Scholl, A. J.: Higher fields of norms and \((\phi ,\Gamma )\)-modules. Documenta Math. 2006, Extra Vol., pp. 685–709 (2006)

    Google Scholar 

  34. Serre, J.-P.: Abelian \(l\)-Adic Representations and Elliptic Curves. Benjamin, W.A (1968)

    MATH  Google Scholar 

  35. Serre, J.-P.: Cohomologie Galoisienne. Springer Lect. Notes Math., vol. 5 (1973)

    Google Scholar 

  36. Thomas, L.: Ramification groups in Artin-Schreier-Witt extensions. J. Théorie des Nombres de Bordeaux 17, 689–720 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  37. Wiles, A.: Higher explicit reciprocity laws. Ann. Math. 107(2), 235–254 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  38. Witt, E.: Zyklische Körper und Algebren der Charakteristik \(p\) vom Grad \(p^n\). Struktur diskret bewerteter perfekter Körper mit vollkommenem Restklassenkörper der Charakteristik \(p\). J. Reine Angew. Math. 176, 126–140 (1936)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mathematisches Institut, Universität Münster, Einsteinstr. 62, 48291, Münster, Germany

    Peter Schneider

  2. Mathematisches Institut, Universität Heidelberg, Im Neuenheimer Feld 288, 69120, Heidelberg, Germany

    Otmar Venjakob

Authors
  1. Peter Schneider
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Otmar Venjakob
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Otmar Venjakob .

Editor information

Editors and Affiliations

  1. Mathematics Institute, University of Warwick, Coventry, United Kingdom

    David Loeffler

  2. Department of Mathematics, University College London, London, United Kingdom

    Sarah Livia Zerbes

Rights and permissions

Reprints and permissions

Copyright information

© 2016 Springer International Publishing Switzerland

About this paper

Cite this paper

Schneider, P., Venjakob, O. (2016). Coates–Wiles Homomorphisms and Iwasawa Cohomology for Lubin–Tate Extensions. In: Loeffler, D., Zerbes, S. (eds) Elliptic Curves, Modular Forms and Iwasawa Theory. JHC70 2015. Springer Proceedings in Mathematics & Statistics, vol 188. Springer, Cham. https://doi.org/10.1007/978-3-319-45032-2_12

Download citation

Publish with us

Policies and ethics

Search

Navigation