Auto Regressive Dynamic Bayesian Network and Its Application in Stock Market Inference

Abstract

In this paper, auto regression between neighboring observed variables is added to Dynamic Bayesian Network (DBN), forming the Auto Regressive Dynamic Bayesian Network (AR-DBN). The detailed mechanism of AR-DBN is specified and inference method is proposed. We take stock market index inference as example and demonstrate the strength of AR-DBN in latent variable inference tasks. Comprehensive experiments are performed on S&P 500 index. The results show the AR-DBN model is capable to infer the market index and aid the prediction of stock price fluctuation.

1 Introduction

Dynamic Bayesian Network (DBN) uses directed graph to model the time dependent relationship in the probabilistic network. The method achieved wide application in gesture recognition [17, 20], acoustic recognition [3, 22], image segmentation [9] and 3D reconstruction [6]. The temporal evolving feature also makes the model suitable to model the stock market [7]. The classic DBN model assumes the observed variable only depend on latent variables, and we know for the instance of stock market, auto regression widely exists in neighboring observed stock prices due to the momentum of market atmosphere. So we introduce explicit auto regressive dependencies between adjacent observed variables in DBN, forming the Auto Regressive Dynamic Bayesian Network (AR-DBN).

In Sect. 2, we have a brief review of previous work in related fields. In Sect. 3, the structure of the network is formed and probability factors are derived. In Sect. 4, we specify the parameter estimation of AR-DBN and experiments are conducted in Sect. 5. Conclusion is reached in Sect. 6.

2 Related Work

Researchers have been using Dynamic Bayesian Networks(DBN) to model the temporal evolution of stock market and other financial instruments [19]. In 2009, Aditya Tayal utilized DBN to analyze the switching of regimes in high frequency stock trading [21]. In 2013, Zheng Li et al. used DBN to explore the dependence structure of elements that influence stock prices [10]. And in 2014, Jangmin O built a price trend model under the DBN framework [7]. Auto regression is an important factor that contribute to the fluctuation of stock prices and has been studied among researchers in financial mathematics [12–14]. Auto regressive relationships among adjacent observed variables is also used in Hidden Markov Models(HMM). In 2009, Matt Shannon et al. illustrated Auto Regressive Hidden Markov Model(AR-HMM) and used it for speech synthesis [18]. In 2010, Chris Barber et al. used AR-HMM to predict short horizon wind with incomplete data [2]. And in 2014, Bing Ai et al. estimated the smart building occupancy with the method [1]. To our knowledge, there haven’t been previous investigation of auto regression applied to Dynamic Bayesian Network (DBN), and in this paper, we integrate the auto regressive property into DBN and forms the Auto Regressive Dynamic Bayesian Network (AR-DBN) (Fig. 1).

Fig. 1.

Overview of work flow for AR-DBN model

3 The Dynamic Bayesian Network for Stock Market Inference

The original DBN before integrating auto regression is shown in Fig. 2. For each time slice i, it includes m observed stock price variables $Y_{1i},...,Y_{mi}$ and hidden variable $X_{i}$. We denote the graph of each slice as $B=(G,\theta )$, where G is the structure of Bayesian Network (BN) for the slice, whose nodes corresponds to the variables and whose edges represent their conditional dependencies, and $\theta$ represents the set of parameters encoding the conditional probabilities of each node variable given its parent [11]. The distribution is represented as CPD (conditional probabilistic distribution) [5]. In our case, as the observed variables are continuous, exact inference is achieved with sum product algorithm [4], which iterate between summation of belief in different states for each clique and combining the belief of neighboring cliques. After the end of each iteration, the marginal probability of each variable is inferred based on likelihood of the whole graph [15].

Fig. 2.

Structure of Dynamic Bayesian Network (DBN)

The likelihood of the graph in Fig. 2 is

$$\begin{aligned} {\begin{matrix} \phi =P(X_{1},Y_{11},...,Y_{m1},X_{2},Y_{12},...,Y_{m2},...,X_{n},Y_{1n},...,Y_{mn}) \end{matrix}} \end{aligned}$$

(1)

Define

$$\begin{aligned}&\phi _{1}=P(X_{1},Y_{11},...,Y_{m1})\\&\phi _{2}=P(X_{1},Y_{11},...,Y_{m1},X_{2},Y_{12},...,Y_{m2})\\&......\\&\phi _{n}=P(X_{1},Y_{11},...,Y_{m1},X_{2},Y_{12},...,Y_{m2},...,X_{n},Y_{1n},...,Y_{mn})\\&\psi _{n}=P(X_{n},Y_{1n},...,Y_{mn})\\&\psi _{n-1}=P(X_{n-1},Y_{1(n-1)},...,Y_{m(n-1)},X_{n},Y_{1n},...,Y_{mn})\\&......\\&\psi _{1}=P(X_{1},Y_{11},...,Y_{m1},X_{2},Y_{12},...,Y_{m2},...,X_{n},Y_{1n},...,Y_{mn})\\ \end{aligned}$$

also define

$$\begin{aligned}&f(X_{i-1},X_{i})=P(X_{i}|X_{i-1})\\&f(X_{i},Y_{1i},...,Y_{mi})=P(Y_{1i},...,Y_{mi}|X_{i}) \end{aligned}$$

Based on sum product algorithm, we have

$$\begin{aligned} \phi _{i}=\Big (\sum _{x_{i-1}}\phi _{i-1}\times f(X_{i-1},X_{i})\Big )\times f(X_{i},Y_{1i},...,Y_{mi}) \end{aligned}$$

(2)

$$\begin{aligned} \psi _{i}=\Big (\sum _{x_{i+1}}\psi _{i+1}\times f(X_{i},X_{i+1})\Big )\times f(X_{i},Y_{1i},...,Y_{mi}) \end{aligned}$$

(3)

And after the belief completes one round bidirectional propagation through the network, the $\phi _{i}$ and $\psi _{i}$ can be readily used to calculate the posterior distribution of each latent variable $X_{i}$

$$\begin{aligned} P(X_{i}|Y) \propto \frac{\phi _{i}\times \psi _{i}}{f(X_{i},Y_{1i},...,Y_{mi})} \end{aligned}$$

(4)

And we can similarly calculate the marginal probability of k consecutive hidden units $X_{i},X_{i+1},...,X_{i+k}$

$$\begin{aligned}&P(X_{i},X_{i+1},...,X_{i+k}|Y) \propto \phi _{i}\times \psi _{i+k} \times f(X_{i},X_{i+1})\times ... \times f(X_{i+k-1},X_{i+k})\nonumber \\&\quad \times f(X_{i+1},Y_{1(i+1)},...,Y_{m(i+1)})\times ... \times f(X_{(i+k-1)},Y_{1(i+k-1)},...,Y_{m(i+k-1)}) \end{aligned}$$

(5)

After the sum product algorithm completes, we can use the marginal probability distribution to estimate the parameters in the network based on EM algorithm.

4 Formulation of Auto Regressive Dynamic Bayesian Network

As mentioned in Sect. 2, due to the ubiquitous auto regressive relationship in stock prices, we can add directed auto regressive edges between neighboring observed variables in the network. The resulting network is shown in Fig. 3. For each observed variable $Y_{ki}$, with the new assumption, it is not only conditioned on the latent variable, but also influenced directly by the previous observed variable.

Fig. 3.

Structure of Auto Regressive Dynamic Bayesian Network (AR-DBN)

For each observed variable, we have

$$\begin{aligned} Y_{t}=\beta _{1}Y_{t-1}+\beta _{2}Y_{t-2}+...+\beta _{k}Y_{t-k}+\alpha U_{t} \end{aligned}$$

(6)

Where k is the depth of the regression, $Y_{t-k}$ to $Y_{t-1}$ is the previous observed variables and $U_{t}$ is directly emitted by the latent variable $X_{t}$. The coefficients satisfy $\beta _{1}+\beta _{2}+...+\beta _{k}+\alpha =1$.

Denote $Y_{t}'=Y_{t}-\beta _{1}Y_{t-1}-\beta _{2}Y_{t-2}-...-\beta _{k}Y_{t-k}$, we have $U_{t}=\alpha ^{-1}Y_{t}'$. From which we can estimate the parameters in AR-DBN, including conditional probability distribution $P(X_{i}|X_{i-1})$, the initial probability distribution $P(X_{1})$ and the emission probability $P(Y_{1i},Y_{2i},...,Y_{ki}|X_{i})$ which can be modeled as a multi variable Gaussian distribution $N(\varvec{\mu },\varvec{\sigma })$.

Based on EM algorithm, we estimate the parameters with marginal probabilities from (4) and (5) by maximizing the first term of KL divergence

$$\begin{aligned}&Q(\theta ,\theta ^{old})=\sum _{X}P(X|Y,\theta ^{old})lnP(X,Y|\theta )\\&=\sum _{X}P(X|\alpha ^{-1}Y',\theta ^{old})ln\Big [P(X_{1}|\pi )\prod _{n=2}^{N}P(X_{n}|X_{n-1},A)\prod _{n=1}^{N}P(\alpha ^{-1}Y_{n}'|X_{n},\phi )\Big ]\\&=\sum _{X}P(X|\alpha ^{-1}Y',\theta ^{old})lnP(X_{1}|\pi )+\sum _{X}P(X|\alpha ^{-1}Y',\theta ^{old})\bigg (\sum _{n=2}^{N}lnP(X_{n}|X_{n-1},A)\bigg )\\&\qquad +\sum _{X}P(X|\alpha ^{-1}Y',\theta ^{old})\bigg (\sum _{n=1}^{N}lnP(\alpha ^{-1}Y_{n}'|X_{n},\phi )\bigg ) \end{aligned}$$

Applying Lagrange method to fulfill the criteria $\,\sum _{k=1}^{K}\pi _{k}=1$ and $\,\sum _{j=1}^{K}A_{ij}=1$ for each $i\,\in \,1,...,K$, where K is the number of states for the hidden variables, the parameters are derived by maximizing

$$\begin{aligned} R=Q(\theta ,\theta ^{old})+\lambda _{1}(\sum _{k=1}^{K}\pi _{k}-1)+\sum _{i=1}^{K}\lambda _{2i}(\sum _{j=1}^{K}A_{ij}-1) \end{aligned}$$

(7)

After setting the first order partial derivatives of R with respect to each individual parameter to zero, the explicit expression of the parameters is derived as below

$$\begin{aligned} \pi _{k}=\frac{P(X_{k}|\alpha ^{-1}Y')}{\sum _{j=1}^{K}P(X_{j}|\alpha ^{-1}Y')} \end{aligned}$$

(8)

$$\begin{aligned} A_{jk}=\frac{\sum _{n=1}^{N-1}P(X_{n}=j,X_{n+1}=k|\alpha ^{-1}Y')}{\sum _{X_{n+1}=1}^{K}\sum _{n=1}^{N-1}P(X_{n}=j,X_{n+1}|\alpha ^{-1}Y')} \end{aligned}$$

(9)

$$\begin{aligned} {\begin{matrix} \mu _{i}=\frac{\sum _{n=1}^{N}P(X_{n}|\alpha ^{-1}Y')Y_{in}}{\sum _{n=1}^{N}P(X_{n}|\alpha ^{-1}Y')} \end{matrix}} \end{aligned}$$

(10)

$$\begin{aligned} {\begin{matrix} \Sigma _{i}=\frac{\sum _{n=1}^{N}P(X_{n}|\alpha ^{-1}Y')(Y_{in}-\mu _{i})(Y_{in}-\mu _{i})^{T}}{\sum _{n=1}^{N}P(X_{n}|\alpha ^{-1}Y')} \end{matrix}} \end{aligned}$$

(11)

Fig. 4.

The visualization of learned CPD. (a) 4 hidden states for each latent variable, (b) 6 hidden states for each latent variable, (c) 8 hidden states for each latent variable.

Fig. 5.

(a) The comparison of log likelihood between DBN and AR-DBN with different number of observed chains. (b) The comparison of log likelihood between different number of latent states in AR-DBN.

Fig. 6.

Trend comparison of inferred latent state with $S \& P$ 500 fluctuation ratio. (a) Inference with 2 observed individual stock chains. (b) Inferrence with 6 observed individual stock chains.

After the training phase completed, we infer the hidden states that form the highest likelihood path with max sum algorithm [8], similar to DBN. The inferred result for the stock market is shown in the next section.

5 Application in Stock Market

We use the historical $S \& P$ 500 stock price dataset provided by Quantquote [16], covering the period from Jan. 02, 1998 to Aug. 09, 2013. The individual stock price temporal fluctuation forms each observed chain and the hidden states are inferred from the multiple observed chains, as shown in Fig. 3. We randomly pick k individual stocks out of the dataset, where k varies in [2,12], then we infer the hidden states and parameters from the data. The trained CPD is visualized and shown in Fig. 4. From which we can see for the inferring task of 6 individual stocks ($k=6$), 8 hidden state is an overkill with first 3 hidden state actually not functioning in transition, while 4 hidden states are not enough to represent all different positions of the market. 6 hidden states is the optimized choice for the model.

Fig. 7.

The micro view of correlation in stock price trends and hidden states. (a) The ascending trend. (b) The descending trend. (c) and (d) The “V” reversal.

Fig. 8.

The Gaussian mixture distribution of the predicted fluctuation and the real price fluctuation for each stock chain, from top left to bottom right corresponds to observed stock price chain 1 to 6.

The AR-DBN outperforms DBN both in the ultimate likelihood achieved and also in the convergence speed, as shown in Fig. 5(a). It reveals that AR-DBN is more suitable and efficient to apply in stock market. The likelihood is also positive correlated with the number of latent states as shown in Fig. 5(b).

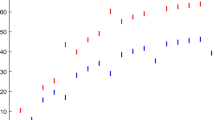
The inferred latent states with max sum algorithm is shown in Fig. 6. The latent states plotted in temporal order form the path that produces highest likelihood in the whole network. The absolute value of increase/decrease ratio in $S \& P$ 500 index is discretized into three intervals $0<ratio<1\,\%$, $1\,\%<ratio<2\,\%$ and $2\,\%<ratio$, then we compare it with the evolving trend of hidden states in Fig. 6. It can be seen that with more observable chains included, the corresponding relationship between the latent states and the market index is more obvious and accurate. With 6 observed individual stock chains, the hidden states in the model is capable to precisely capture the fluctuation of market index. Take Fig. 6(b) for example, state 1 and state 2 capture the characteristics of the fast changing market, while the other states reflect the time when the market is smooth. The hidden states have a direct reflection of the individual stock prices if we use absolute value of the price as the observed variable. Important trends in the price movement such as ascending trend, descending trend and “V” reversal are reflected in hidden states as shown in Fig. 7.

The AR-DBN stock market model we generated is not only useful to unveil market rules contained in historical stock price, it can also support investment decision making based on probabilistic prediction of the near future. In this application, we predict price movement direction (upward/downward) of the 6 observed stocks for the first day following the end of chain based on the parameters we learned. We multiply the latent states inferred from the max sum algorithm with the conditional probability distribution $P(X_{t+1}|X_{t})$ and turns the future stock price $Y_{t+1}$ into a Gaussian mixture distribution conditioned on the probability distribution of future latent states $X_{t+1}$. The prediction result together with the real fluctuation for each of the stocks is shown in Fig. 8. For 5 out of the 6 stocks, the centroid of the probability distribution are of the same direction (upward/downward) with the real price trend, which shows our model can help with the prediction of fluctuation direction.

6 Conclusion and Future Work

We derived Auto Regressive Dynamic Bayesian Network (AR-DBN) by adding auto regression among the adjacent observed variables in Dynamic Bayesian Network (DBN). We presented a new approach to model the stock market based on the proposed AR-DBN and comprehensive inference tasks were implemented with the model. The results showed the latent variables in the model accurately inferred the market index fluctuation and the stock price trends.

In this paper, we mainly focused on the inference part of the model. There is more work to be done with quantitative prediction of future price fluctuations and also the application of AR-DBN to other temporal analysis domains. We leave this for future work.