Abstract
As it is the case for linear systems, understanding the influence of interconnections on stability and asymptotic behavior is of paramount importance. In the case of nonlinear systems, a powerful concept in the analysis of interconnections is the notion of gain function of an input-to-state stable system. Using this concept, it is possible to develop a nonlinear version of the small-gain theorem, which is useful in the analysis as well as in the design of feedback laws. This chapter describes this theorem and how it can be used in the design of stabilizing feedback laws for nonlinear systems.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
More precisely, if the \({\mathscr {L}}_2\) gains of the two component systems are upper-bounded by two numbers \(\bar{\gamma }_1\) and \( \bar{\gamma }_2\) satisfying \(\bar{\gamma }_1\bar{\gamma }_2 \le 1\).
- 2.
See [9] for an introduction to the property of input-to-state stability.
- 3.
A function \(\gamma : [0,\infty ) \rightarrow [0,\infty )\) satisfying \(\gamma (0)=0\) and \(\gamma (r)<r\) for all \(r>0\) is called a simple contraction. Observe that if \(\gamma _1\circ \gamma _2(\cdot )\) is a simple contraction, then also \(\gamma _2\circ \gamma _1(\cdot )\) is a simple contraction. In fact, let \(\gamma _1^{-1}(\cdot )\) denote the inverse of the function \(\gamma _1(\cdot )\), which is defined on an interval of the form \([0,r_1^*)\) where
$$ r_1^*= \lim _{r \rightarrow \infty }\gamma _1(r). $$If \(\gamma _1\circ \gamma _2(\cdot )\) is a simple contraction, then
$$ \gamma _2(r)< \gamma _1^{-1}(r) \;\;\mathrm{for}\;\;\mathrm{all}\;\;0<r<r_1^*, $$and this shows that
$$ \gamma _2(\gamma _1(r)) <r\;\;\mathrm{for}\;\;\mathrm{all}\;\;r>0, $$i.e., \(\gamma _2\circ \gamma _1(\cdot )\) is a simple contraction .
- 4.
- 5.
The reader should have no difficulty in checking that a function defined as
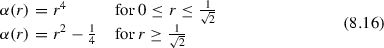
has the indicated property.
- 6.
See [1] for further results of this kind.
- 7.
Use the fact that \(x\alpha (x) = |x|\alpha (|x|).\)
- 8.
Note that the resulting system is a special case of the system in Fig. 8.2, namely the interconnection of
$$ \dot{x} = q(v_1,x) + b(v_2)u \quad z = x \quad y = x $$and
$$ \begin{array}{rcl} \dot{x}_\mathrm{p} &{}=&{} f_\mathrm{p}(x_\mathrm{p},z)\\ \dot{\mu }&{}=&{} 0\end{array} \quad \begin{array}{rcl} v_1 &{}=&{} x_\mathrm{p}\\ v_2 &{}=&{} \mu \end{array}$$with control \(u=h_\mathrm{c}(y)\).
- 9.
- 10.
See also [12].
References
J.M. Coron, L. Praly, A.R. Teel, Feedback stabilization of nonlinear systems: sufficient conditions and Lyapunov and input–output techniques, in Trends in Control, ed. by A. Isidori (Springer, London, 1995), pp. 293–348
D. Hill, P.J. Moylan, The stability of nonlinear dissipative systems. IEEE Trans. Autom. Control AC–21, 708–711 (1976)
D. Hill, P.J. Moylan, Stability results for nonlinear feedback systems. Automatica 13, 377–382 (1977)
D. Hill, P.J. Moylan, Connections between finite gain and asymptotic stability. IEEE Trans. Autom. Control AC–25, 931–935 (1980)
A.K. Imai, R.R. Costa, L. Hsu, G. Tao, P.V. Kokotovic, Multivariable adaptive control using high-frequency gain matrix factorization. IEEE Trans. Autom. Control 49(7), 1152–1157 (2004)
Z.P. Jiang, A.R. Teel, L. Praly, Small-gain theorem for ISS systems and applications. Math. Control Signal Syst. 7, 95–120 (1994)
Z.P. Jiang, I.M.Y. Mareels, Y. Wang, A Lyapunov formulation of the nonlinear-small gain theorem for interconnected ISS systems. Automatica 32, 1211–1215 (1996)
A.S. Morse, A gain matrix decomposition and some of its applications. Syst. Control Lett. 21, 1–10 (1993)
E.D. Sontag, On the input-to-state stability property. Eur. J. Control 1, 24–36 (1995)
A. Teel, A nonlinear small gain theorem for the analysis of control systems with saturations. IEEE Trans. Autom. Control AC–41, 1256–1270 (1996)
M. Vidyasagar, Decomposition techniques for large-scale systems with nonadditive interactions: stability and stabilizability. IEEE Trans. Autom. Control AC–25, 773–779 (1980)
L. Wang, A. Isidori, H. Su, Global stabilization of a class of invertible MIMO nonlinear systems. IEEE Trans. Autom. Control 60, 616–631 (2015)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2017 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Isidori, A. (2017). The Small-Gain Theorem for Nonlinear Systems and Its Applications to Robust Stability. In: Lectures in Feedback Design for Multivariable Systems. Advanced Textbooks in Control and Signal Processing. Springer, Cham. https://doi.org/10.1007/978-3-319-42031-8_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-42031-8_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-42030-1
Online ISBN: 978-3-319-42031-8
eBook Packages: EngineeringEngineering (R0)