Effectively Propositional Interpolants

Abstract

We present a novel interpolation algorithm for effectively propositional logic (epr), a decidable fragment of first-order logic that enjoys a small-model property. epr is a powerful fragment of quantified formulas that has been used to model and verify a range of programs, including heap-manipulating programs and distributed protocols. Our interpolation technique samples finite models from two sides of the interpolation problem and generalizes them to learn a quantified interpolant. Our results demonstrate our technique’s ability to compute universally-quantified, existentially-quantified, as well as alternation-free interpolants and inductive invariants, thus improving the state of the art.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Craig interpolation techniques have played an important role in the advancement of automated analysis and verification: from hardware verification [18], to software verification [12, 19], to error diagnosis [10], and even to modeling of cyber-physical systems [4]. By representing program executions as first-order formulas, interpolants can be used to concisely conjecture why the program is correct. Expanding the scope of interpolation-based verification requires investigating and developing interpolation techniques for different logical theories that enable modeling of various program features.

In this paper, we investigate the problem of computing Craig interpolants for effectively propositional logic (epr), also known as the Bernays-Schönfinkel-Ramsey fragment of first-order logic. epr is the class of formulas of the form $\exists ^*\forall ^* \varphi$, where the quantifier-free formula $\varphi$ has no function symbols. Two interesting aspects motivate our study of this fragment: (i) decidability of its satisfiability and (ii) its surprising applicability to modeling a range of complex program features. For instance, epr has been used to model programs manipulating linked-list data structures and arrays [13–15, 17, 26], software-defined networking programs [5], eventually consistent data stores [29], parameterized distributed protocols [22], amongst others [23–25]. Indeed, the power of epr lies primarily in its ability to model unbounded structures. Thus, progress in interpolation can open the door to verification in a large spectrum of domains.

We propose a sampling-based technique for computing an interpolant I for two inconsistent epr formulas, A and B. A key insight in our approach is that we can use an epr satisfiability procedure as an oracle to systematically sample finite models of A and B and generalize them to monotonically grow an interpolant. A finite model of an epr formula can be viewed as a relational structure—a hypergraph—over a finite set of nodes. Our algorithm thus samples hypergraphs from A and B and generalizes them into infinite sets of structurally similar hypergraphs.

Our presented technique ensures that computed interpolants do not contain quantifier alternation—that is, they are of the form $\exists ^*\varphi$, $\forall ^*\varphi$, or Boolean combinations of those. This pragmatic constraint is motivated by the fact that computed interpolants are typically used in verification engines, and thus form inductive invariant conjectures. To check if an interpolant $I(\varvec{x})$ is an inductive invariant with respect to a transition relation $T(\varvec{x},\varvec{x}')$, one needs to check satisfiability of $I(\varvec{x}) \wedge T(\varvec{x},\varvec{x}') \wedge \lnot I(\varvec{x}')$. If I has quantifier alternation, we leave the decidable confines of the epr fragment—due to the negation of I, which makes it of the form $\forall ^*\exists ^*\varphi$. Thus, by finding alternation-free interpolants, we maintain decidability of inductiveness checking.

Contributions. To our knowledge, this paper is the first comprehensive investigation of epr interpolation. We summarize our key contributions as follows:

• We first present an interpolation algorithm that can construct an existentially-quantified interpolant, of the form $\exists ^* \varphi$, or detect its non-existence. The algorithm monotonically grows an interpolant by sampling finite models and generalizing them using the model-theoretic notion of diagrams [9].

• We present an interesting proof of soundness and completeness of our algorithm and identify epr fragments and conditions for which it is complete.

• We show that, by solving the dual interpolation problem, our algorithm can also be used to construct universally-quantified interpolants, of the form $\forall ^* \varphi$.

• We then show how, by systematically decomposing the interpolation problem, we can leverage this procedure to construct alternation-free interpolants with Boolean combinations of universal and existential quantifiers.

• We validate our interpolation algorithm by implementing it alongside a simple interpolation-based verifier. We show that the verifier (i) is competitive with recent pdr-based algorithms [15, 17] for computing universal invariants, and (ii) is able to compute alternation-free invariants, a fragment that is out of scope for existing techniques.

2 Illustrative Example

In this section, we illustrate our technique with simple examples.

Fig. 1.

High-level illustration of unidirectional interpolation.

Existential Interpolants. Consider the following formulas in epr:

where p, q, r, s are unary relations. $A \wedge B$ is unsatisfiable, and we would like to find an interpolant I such that (i) $A \Rightarrow I$, (ii) $I \Rightarrow \lnot B$, and (iii) I is over the shared vocabulary of A and B: the relations p and q, only.

We will search for an interpolant in epr that is restricted to existential quantifiers, i.e., contains no universal quantifiers. To do so, we will use an algorithm we call unidirectional interpolation (uitp), illustrated at a high-level in Fig. 1. uitp grows an interpolant by sampling models of A only (hence, unidirectional) and generalizing them. epr satisfiability is decidable and epr formulas have finite models, which we can find using a reduction to sat (or using, e.g., the Z3 smt solver [20]). The problem is that models in this fragment correspond to a universe of anonymous elements that satisfy the formula. The question is: how can we generalize such a model to a set of models and represent it as a formula?

Let us begin by sampling the following model (structure) m from A: the singleton universe of elements $\{u_1\}$, where $p(u_1)$ and $r(u_1)$ hold, but $q(u_1)$ does not. Observe that this model satisfies A, denoted $m \models A$. Now, we can generalize this model to a set of models using the model-theoretic notion of diagrams [9, 17], restricted to the shared vocabulary of A and B.

A diagram is analogous to a cube in the propositional setting, in that it is a conjunction of the facts the model satisfies. However, since our model is a collection of anonymous elements, we need to abstract them using quantified variables as follows:

There are three important aspects to observe:

• (i) $m \models diag (m)$, and the diagram generalized m to a set of infinitely many models that have at least one element satisfying p but not q;

• (ii) the relation r does not appear in the diagram, since it is not in the shared vocabulary of A and B; and

• (iii) $diag (m) \wedge B$ is unsatisfiable.

At a high-level, a model defines a relational structure between a set of elements—perhaps a graph, linked list, or tree. Generically, models represent hypergraphs. A diagram then abstracts a model into a formula defining an infinite set of structurally similar hypergraphs, as illustrated in Fig. 2.

Fig. 2.

Illustration of diagrams as sets of models

Our goal is to sample enough models such that the disjunction of their diagrams covers (subsumes) A and is unsatisfiable with B. In this example, A is not subsumed by $diag (m)$, and therefore we sample a model of A that is not a model of $diag (m)$. Suppose we get the model $m'$ with the universe $\{u_2\}$, where $q(u_2)$ and $r(u_2)$ hold, but $p(u_2)$ does not. From $m'$, we construct the following:

The formula $diag (m')$ is unsatisfiable with B, but together with $diag (m)$ does not yet subsume A. We sample a third model of A that is neither a model of $diag (m)$ nor $diag (m')$. Suppose we get the model $m''$ with the universe $\{u_3\}$, where $p(u_3)$, $q(u_3)$, and $r(u_3)$ hold. From $m''$, we construct the following: . The formula $diag (m'')$ is unsatisfiable with B and, together with $diag (m)$ and $diag (m')$, subsumes A. Therefore,

$$\begin{aligned} diag (m) \vee diag (m') \vee diag (m'') \end{aligned}$$

is an interpolant of (A, B). In practice, we weaken the interpolant further, and hasten convergence, by dropping unnecessary conjuncts appearing in the diagrams; we do so using unsat cores, as described in Sect. 4.1.

Detecting that no Interpolant Exists. Not all epr formulas have existentially-quantified interpolants. Consider the following example [7]:

An interpolant for A and B has to have a quantifier alternation, for instance, . If we run uitp on the pair (A, B), we can detect that no existentially-quantified interpolant exists. Suppose that we sample the model m with universe $\{u\}$ where p(u, u) holds. Then, $diag (m)$ is . This diagram is satisfiable with B (see Fig. 1(c)). A diagram of m is the strongest possible existentially-quantified formula in the shared vocabulary of (A, B) for which m is a model; therefore, we can conclude that there is no existentially-quantified interpolant for (A, B).

Universal Interpolants. Suppose that a pair of formulas (A, B) only has a universally-quantified interpolant. By definition of an interpolant, this means that the dual interpolation problem over (B, A) has an existentially-quantified interpolant. Therefore, to compute a universally-quantified interpolant for (A, B), we can simply use uitp to compute an interpolant for (B, A) and negate it, as negation flips the existential quantifier into a universal one (see Sect. 4.1).

Alternation-Free Interpolants. Let us now consider an example that requires a Boolean combination of $\exists ^*\varphi$ and $\forall ^*\varphi$ formulas—i.e., an alternation-free epr formula. The uitp algorithm described above is insufficient in this case, as it cannot compute interpolants with Boolean combinations of existential and universal quantifiers. To construct such an interpolant, we will use uitp as a sub-procedure, but we will decompose the interpolation problem and invoke uitp on a dual problem when requiring universal quantifiers. We call this approach bidirectional interpolation, bitp, as it alternates sampling between the A and B sides of the interpolation problem.

Fig. 3.

High-level illustration of one recursive step of bidirectional interpolation.

Consider the following interpolation problem:

We begin by invoking uitp on the above, and it will immediately discover a model m of A whose diagram overlaps with B. Suppose uitp discovers the following diagram for some model m:

It happens that $diag (m)$ overlaps with B. Intuitively, the region of overlap, $diag (m) \wedge B$, cannot be isolated by the interpolant using only existential quantifiers. Therefore, we need to strengthen the diagram using a universal formula. To do so, we attempt to find a universal interpolant between $diag (m) \wedge A$ and $diag (m) \wedge B$. Specifically, we invoke uitp on the interpolation problem

$$\begin{aligned} (diag (m) \wedge B, diag (m) \wedge A) \end{aligned}$$

and negate the result—this produces a universally-quantified formula with which we can strengthen $diag (m)$. Notice that B now appears on the left side of the interpolation problem; thus, sampling now proceeds from the region in B that overlaps with $diag (m)$ (see Fig. 3 for an illustration).

Once we get a universal interpolant, we use it to strengthen $diag (m)$. In this example, after more sampling, we finally arrive at the following interpolant:

We have demonstrated how bitp uses uitp as a base procedure to compute alternation-free interpolants. In a nutshell, the algorithm proceeds as if an existential interpolant exists, and when it finds out that is not the case, it switches direction to find the universal subformulas required to strengthen the interpolant. We describe this process in detail in Sect. 4.3.

3 Preliminaries

In this section, we formalize definitions needed for the rest of the paper.

Effectively Propositional Logic. We shall use $\mathcal {L}$ to denote the class of all epr formulas. An epr formula $\psi$ is a first-order formula that, when written in prenex normal form, is of the form

where $x_i$ and $y_i$ are quantified variables, and $\varphi$ is a quantifier-free formula over quantified variables, free variables, and relations. Note that $\varphi$ has no function symbols. (We elide constants for clarity of presentation.) Throughout the paper, we shall refer to epr formulas as if they are written in prenex normal form. We shall use $vocab (\psi )$ to denote the set of free variables and relation symbols appearing in $\psi$. We shall also refer to the following epr subfragments:

• $\mathcal {L}_\forall$: the class of formulas that only contain universal quantifiers,

• $\mathcal {L}_\exists$: the class of formulas that only contain existential quantifiers, and

• $\mathcal {L}_{\textsc {{af}}}$: the class of formulas that do not contain quantifier alternation.

Observe that $(\mathcal {L}_\exists \cup \mathcal {L}_\forall ) \subset \mathcal {L}_{\textsc {{af}}}\subset \mathcal {L}$.

Finite Models. Given a $\mathcal {L}$ formula $\psi$ with a set V of free variables and a set R of relation symbols, a finite model m of $\psi$, denoted $m \models \psi$, is a tuple (U, A, T), where

• U is a finite set of elements, called the universe of m;

• A is an assignment function mapping free variables V and existentially-quantified variables of $\psi$ to elements of U; and

• T is an interpretation function that maps each relation $r \in R$ to a set of tuples over U such that, for r with arity n, $(u_1, ..., u_n) \in U^n$ is in the relation r if and only if $(u_1, ..., u_n) \in T(r)$.

As is standard, given a model m of $\psi$, if $\psi$ is instantiated with A and T, it evaluates to $true$ under the universe U. The cardinality of m is the size of its universe. Despite the fact that $\mathcal {L}$ formulas may have infinite models, we will always use model to refer to finite models.

It is important to note that formulas in $\mathcal {L}$ have a small-model property, meaning that a formula is satisfiable iff it has a model whose universe is smaller than or equal to the sum of the number of free and existentially-quantified variables (see Theorem 3 below).

Diagrams. We now define the model-theoretic notion of a diagram, which allows us to abstract a model m into a set of models.

Given a model $m = (U, A, T)$, a set of variables V, and a set of relations R, we construct the diagram of m with respect to V and R, denoted $diag (m,V,R)$ (or $diag (m)$, when V and R are clear from context) as follows:

• For each element $u_i \in U$, introduce a fresh variable $x_{u_i}$.

• Let $\varphi _{elem }$ be the conjunction of the following terms:

  • For each distinct $u_i, u_j \in U$, the term $x_{u_i} \ne x_{u_j}$.

  • For each $x \in V$, the term $x = x_{u}$, where $A(x) = u$.

• Let $\varphi _{rel }$ be the conjunction of terms described as follows:

  • For each $r \in R$ and $(u_1,\ldots ,u_n) \in T(r)$, the term $r(x_{u_1},\ldots ,x_{u_n})$.

  • For each $r \in R$ and $(u_1,\ldots ,u_n) \not \in T(r)$, the term $\lnot r(x_{u_1},\ldots ,x_{u_n})$.

• Finally,

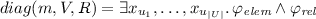
Observe that $m \models diag (m,V,R)$. The diagram abstracts the anonymous elements of the universe of a model as existential variables. As a result the diagram of m is the set of all models that have a substructure isomorphic to m (see definition of substructure below, and recall Fig. 2 for a visualization).

Example 1

Let . A possible model $m \models \psi$ is:

• $U = \{u_1, u_2\}$

• $A = \{ x \mapsto u_2\}$

• $T = \{P \mapsto \{(u_2)\}, Q \mapsto \emptyset \}$

The diagram of the model m with respect to $V = \{x\}$ and $R = \{P\}$ is:

If we had considered instead a model $m'$ with a single element in its universe, we would have obtained that $diag(m',V,R)$ is .    $\blacksquare$

Substructure. We briefly define the model-theoretic substructure relation. Given a model $m = (U, A, T)$, a substructure of m is a model $m' = (U',A',T')$ such that $U' \subset U$ and $A'$ and $T'$ are restrictions of A and T to $U'$. We will use $m' \preceq m$ to denote that $m'$ is isomorphic to a substructure of m. The notion of a substructure admits many desirable properties:

Theorem 1

If $m_1 \preceq m_2$ and $\varphi \in \mathcal {L}_\exists$, then $m_1 \models \varphi \Rightarrow m_2 \models \varphi$.

Corollary 1

$m_1 \preceq m_2$ if and only if $m_2 \models diag (m_1)$.

Proof

The forward direction is a consequence of Theorem 1. For the reverse, if $m_2 \models diag (m_1)$, then, by construction of $diag$, there is a subset of $m_2$ that is isomorphic to $m_1$, so $m_1 \preceq m_2$.    $\blacksquare$

Theorem 2

If $m_1 \preceq m_2$ and $\varphi \in \mathcal {L}_\forall$, then $m_2 \models \varphi \Rightarrow m_1 \models \varphi$.

Corollary 2

Given $\varphi \in \mathcal {L}_{\textsc {{af}}}$, written as a Boolean combination of $\mathcal {L}_\forall$ and $\mathcal {L}_\exists$ subformulas, if $m_1 \preceq m_2$ and each $\mathcal {L}_\exists$ subformula $\psi$ of $\varphi$ has the property that $m_2 \models \psi \Rightarrow m_1 \models \psi$, then $m_2 \models \varphi \Rightarrow m_1 \models \varphi$.

Proof

From the given and from Theorem 2, we know that $m_1$ satisfies at least as many subformulas of $\varphi$ as $m_2$ does, and thus $m_1 \models \varphi$.    $\blacksquare$

Small Models. Additionally, given an arbitrary model $m \models \varphi$ for $\varphi \in \mathcal {L}$, there exists a small model $m' \preceq m$ such that $m' \models \varphi$.

Theorem 3

If $\varphi$ is a satisfiable epr formula written in prenex normal form

where $c_1, \ldots , c_\ell$ are free variables, then there exists a model of $\varphi$ with size $|U| \leqslant n + \ell$.

Proof

Let m be a model of $\varphi$. Consider $m' = (U', A, T')$ where

• $U'$ is the restriction of U to $\varphi$, i.e. the elements to which existentially-quantified variables $x_1, \ldots , x_n$ and free variables $c_1, \ldots , c_\ell$ are mapped.

• $T'$ is the restriction of T to $U'$.

Then, it follows immediately that $m'$ is also a model of $\varphi$ with $U' \leqslant n + \ell$.    $\blacksquare$

Interpolants. Given a pair of $\mathcal {L}$ formulas, (A, B), where $A \wedge B$ is unsatisfiable, an interpolant I for the interpolation problem (A, B) is a formula such that

• $A \Rightarrow I$ is valid,

• $I \Rightarrow \lnot B$ is valid, and

• $vocab (I) \subseteq vocab (A) \cap vocab (B)$.

Given an interpolation problem (A, B), we call (B, A) the dual interpolation problem. For the purposes of this paper, we will restrict interpolants to formulas in the alternation-free subfragment of $\textsc {{epr}}$, namely, $\mathcal {L}_{\textsc {{af}}}$.

4 Effectively Propositional Interpolation

In this section, we describe our algorithms for computing interpolants for epr formulas. We first present a unidirectional interpolation algorithm, which can compute interpolants in $\mathcal {L}_\exists$ and $\mathcal {L}_\forall$ by sampling from one side (i.e., formula) of the interpolation problem. We then discuss bidirectional interpolation, which alternates its sampling between the two sides to construct an interpolant in $\mathcal {L}_{\textsc {{af}}}$.

4.1 Unidirectional Interpolation

Algorithm Description. The unidirectional interpolation algorithm, uitp, is used to find an interpolant in $\mathcal {L}_\exists$ for a pair of formulas (A, B) or to detect that no such interpolant exists. The high-level idea is to grow an interpolant—starting from $false$—by sampling models of A. Of course, A likely has infinitely many models; the algorithm thus generalizes sampled models using diagrams until they subsume all of A or until a model’s diagram overlaps with B, in which case we know there does not exist an existentially-quantified interpolant.

uitp is presented in Algorithm 1 as a set of guarded rules that update a set of samples S, which contains diagrams of models of A. Initially, the set S is empty; the rule $\textsc {{sample}}$ finds a model of A that is not a model of one of the diagrams in S and adds its diagram to S. The diagrams are taken with respect to the set of variables V and relations R in the shared vocabulary, $vocab (A) \cap vocab (B)$.

Observe that S is a set of existentially-quantified formulas of the form

where $a_i$ is an atomic predicate. At any point the candidate interpolant is $\bigvee S$, i.e., the disjunction of all diagrams in S. Thus, the candidate interpolant begins as being $false$, and every time the rule $\textsc {{sample}}$ is applied, the candidate interpolant is weakened. Note that all formulas in $\mathcal {L}_\exists$ can be written as disjunctions of existentially-quantified conjunctions of atoms.

The algorithm succeeds in finding an interpolant when the rule $\textsc {{itp}}$ applies—that is, when $A \Rightarrow \bigvee S$ and $\bigvee S \Rightarrow \lnot B$ are valid. Observe that all of these satisfiability checks lie within epr, and are therefore decidable.

If the algorithm detects a diagram in S that is satisfiable with B, using rule $\textsc {{fail}}$, it concludes that no interpolant in $\mathcal {L}_\exists$ exists for (A, B). The intuition here is as follows: Given a model $m \models A$, $diag (m)$ is the strongest formula in $\mathcal {L}_\exists$ for which m is a model. Therefore, if $diag (m)$ overlaps with B, we cannot find an interpolant in $\mathcal {L}_\exists$ that includes the model m. (See Theorem 5.)

Finally, the rule $\textsc {{abstract}}$ attempts to weaken a diagram up to B—that is, it takes a diagram in S and removes some of its conjuncts such that the result is still unsatisfiable with B. In practice, this is performed using unsat cores, when checking whether the diagram is satisfiable with B. Whereas this rule is not needed for soundness or completeness, it is of crucial importance in practice, as otherwise diagrams are overly specific (this is further discussed below).

Computing $\mathcal {L}_\forall$ Interpolants. uitp can also be used to compute universally-quantified interpolants in $\mathcal {L}_\forall$. This can be easily done as follows: Suppose that (A, B) has an interpolant $I_\forall$ in $\mathcal {L}_\forall$. By definition of an interpolant, we know that

• (i) $B \Rightarrow \lnot I_\forall$ is valid and

• (ii) $\lnot I_\forall \Rightarrow \lnot A$ is valid.

In other words, $\lnot I_\forall$ is an interpolant for the dual interpolation problem, (B, A). Observe that $\lnot I_\forall$ is in $\mathcal {L}_\exists$, since the negation turns the universal quantifier into an existential one. Therefore, to find a universal interpolant for (A, B), we can simply use uitp to find an existential interpolant for (B, A) and take its negation. Viewed differently, by solving the dual interpolation problem, we are essentially modifying uitp to sample from the B side of the interpolation problem instead of the A side, and this allows us to compute universally-quantified interpolants.

Interpolant Strength. For any two formulas, there is typically a spectrum of interpolants. Depending on the order in which the uitp rules are applied, we may arrive at different interpolants.

On one extreme, if we avoid using the $\textsc {{abstract}}$ rule, we ensure that whatever interpolant we find is the strongest possible one. This is because, for every sampled model m of A, uitp will add the strongest possible formula in $\mathcal {L}_\exists$ that contains m (its diagram) to the set of samples S. Any interpolant that is stronger will thus have to exclude one of the models of A.

On the other extreme, if at every step $\textsc {{abstract}}$ is applied exhaustively—i.e., until it is no longer applicable to any $s \in S$—then we arrive at a maximal interpolant. (This is equivalent to taking a minimal unsat core of each diagram with respect to B, which can result in sampling exponentially fewer models.) A maximal interpolant I is one that cannot be weakened while remaining an interpolant—i.e., there does not exist an interpolant $I'$ such that $I \Rightarrow I'$ and $I \not \equiv I'$. Note that there maybe a number of incomparable maximal interpolants.

The following theorem states that different applications of the rules can result in all interpolants, from the weakest to the strongest.

Theorem 4

For every interpolant $I \in \mathcal {L}_\exists$ of (A, B), there exists a run of $\textsc {{uitp}}$ that will compute it.

4.2 Theoretical Properties of uitp

We now investigate soundness and completeness of uitp.

Soundness. The following theorem states that uitp is sound.

Theorem 5

(Soundness). If uitp, invoked on (A, B), returns a formula $I \in \mathcal {L}_\exists$, then I is an interpolant of (A, B). If the fail rule applies, then there is no interpolant in $\mathcal {L}_\exists$ for (A, B).

Proof

The first statement follows from the fact that (i) the candidate interpolant $\bigvee S$ is in $\mathcal {L}_\exists$; (ii) following the rule sample, the candidate interpolant is over the shared vocabulary of A and B; and (iii) the rule $\textsc {{itp}}$ ensures that the returned formula I is such that $A \Rightarrow I$ and $I \Rightarrow \lnot B$.

We prove the latter statement by contradiction. Suppose $I \in \mathcal {L}_\exists$ is an interpolant for (A, B), but the fail rule applies. Then, there is a model $m \models A$ such that $diag (m) \wedge B$ is satisfiable. I can be written as $\bigvee _i \psi _i$, where $\psi _i$ is an $\mathcal {L}_\exists$ formula of the form $\exists ^*\varphi _i$, where $\varphi _i$ is a conjunction of atoms. If $m \models A$, then, since I subsumes A, $m \models I$. In particular, for some i, $m \models \exists ^* \varphi _i$. By construction, $diag (m)$ is at least as strong as $\exists ^* \varphi _i$, so since $diag(m) \wedge B$ is satisfiable, so is $I \wedge B$—but this contradicts the definition of an interpolant.    $\blacksquare$

Completeness. We now consider completeness of uitp: meaning that it is always able to find an interpolant if one exists or detect its non-existence in a finite number of steps. The key insight in our proof is the observation that every $\textsc {{epr}}$ formula A has a finite set of small models that characterize an $\mathcal {L}_\exists$ formula that subsumes A. The following lemma formalizes this observation, which we prove using epr ’s small-model property.

Lemma 1

( $\mathcal {L}_\exists$ basis). Given $A \in \mathcal {L}$, let $M = \{m \mid m\text { is a small model of } A\}$. Then M is a finite set, called an $\mathcal {L}_\exists$ basis, such that

$$\begin{aligned} A \Rightarrow \left( \bigvee _{m \in M} \textit{diag}(m)\right) \text { is valid.} \end{aligned}$$

(1)

Proof

For any model $m \models A$, there is a small model $m' \models A$ such that $m' \preceq m$, and therefore $diag (m) \Rightarrow diag(m')$. It follows that every model of A is a model of $\bigvee _{m \in M} diag (m)$, and since the small models have an upper bound on their cardinality, there are finitely many of them. Therefore, Formula 1 is well-formed and holds.    $\blacksquare$

Using Lemma 1, we are now ready to state completeness of uitp. The following theorem assumes a fair application of uitp rules.

Theorem 6

(Completeness of UITP ). Let c be the maximum of the small-model cardinality bounds of A and B. If uitp is invoked under the additional constraint that each sampled model has cardinality at most c, then eventually one of the rules $\textsc {{itp}}$ or $\textsc {{fail}}$ applies.

Proof

First, consider the case that an interpolant exists. By Lemma 1, A has an $\mathcal {L}_\exists$ basis $M'$ where each model has size at most c. So, if an interpolant exists in $\mathcal {L}_\exists$, we eventually find it by enumerating the finitely many models (up to isomorphism) of size at most c.

Second, consider the case where no interpolant exists. The algorithm will eventually find a model $m\models A$ such that $diag (m) \wedge B$ is satisfiable. This follows from Lemma 1, as if no such model is found, the existence of an $\mathcal {L}_\exists$ basis would induce an interpolant.    $\blacksquare$

Complete Theories. The above completeness theorem assumes that sampling produces models of bounded cardinality. This can be enforced by adding the constraint $card (c)$ to the formula:

(2)

$card (c)$ restricts sampling to models of size at most c. In practice, however, we are typically operating on formulas from a specific domain, which might have desirable properties that allow us to elide the potentially costly cardinality restriction for completeness.

Consider, for example, epr formulas representing linear orders [14, 21], which can be used to model linked and doubly-linked lists. Linear orders restrict relations to be at most of binary arity and to be reflexive, transitive, and anti-symmetric. We shall call this subset of formulas $\mathcal {L}_{\textsc {{lo}}}$. As very recently discovered by Padon et al. [21], this epr theory forces a well-quasi-order on models. This ensures that there is no infinite sequence of models that are incomparable according to the substructure relation. Using this result, we can show that uitp is complete for $\mathcal {L}_{\textsc {{lo}}}$, without the model cardinality restrictions from Theorem 6.

Theorem 7

(Completeness under linear ordering). Given $A,B \in \mathcal {L}_{\textsc {{lo}}}$, if uitp is invoked on (A, B), it eventually terminates.

Proof

We prove this by contradiction. Suppose that uitp does not terminate on some (A, B). Then, there are infinitely many calls to $\textsc {{sample}}$, and therefore an infinite sequence of computed models $m_1, m_2, \ldots$ of A. By Padon et al. [21, Theorem 6.2], we know that this sequence of models forms a well-quasi-order that is equivalent to the substructure relation: there exist models $m_i$ and $m_j$, with $i < j$, such that $m_i \preceq m_j$. This means that $m_j \models diag (m_i)$, which cannot happen by definition of $\textsc {{sample}}$: once we have considered $m_i$, we only obtain model $m_j$ if $m_j \not \models diag (m_i)$.    $\blacksquare$

The proof of the above theorem only exploits the fact that models of $\mathcal {L}_{\textsc {{lo}}}$ form a well-quasi-order under the $\sqsubseteq _{\forall ^*}$ ordering of Padon et al. [21, Theorem 6.2]. Thus, as a direct corollary, we can show completeness of uitp for any theory with such property—and not only linear orders.

4.3 Bidirectional Interpolation

Algorithm Description. We now switch attention to computing alternation-free interpolants in $\mathcal {L}_{\textsc {{af}}}$, i.e., with Boolean combinations of formulas in $\mathcal {L}_\exists$ and $\mathcal {L}_\forall$. Recall that, by solving the dual interpolation problem, we can compute universal interpolants using uitp. Bidirectional interpolation exploits this property to compute interpolants in $\mathcal {L}_{\textsc {{af}}}$. Specifically, bitp proceeds as if an $\mathcal {L}_\exists$ interpolant exists, and when it discovers that it is not the case, it recursively switches to solving a dual interpolation problem in order to find the required subformulas needed to strengthen the interpolant.

bitp is described in Algorithm 2. bitp uses the rules of uitp to construct an interpolant, and, like uitp, maintains the set of diagrams S and a candidate interpolant $\bigvee S$. The algorithm begins by applying $\textsc {{init}}$ and iteratively samples models, using $\textsc {{sample}}$, until an interpolant is found. When an $\mathcal {L}_\exists$ interpolant exists, $\textsc {{bitp}}$ behaves as a determinization of uitp ’s rules. The difference from uitp, however, is when a diagram $s \in S$ overlaps with B.

Recall that sampling adds $\mathcal {L}_\exists$ formulas to S. If one $s \in S$ overlaps with B, we attempt to strengthen it with a universally-quantified formula by recursively calling $\textsc {{bitp}}$ on $(s \wedge B, s \wedge A)$ and negating the result (see lines 5 and 6). In other words, we focus on the region in B that overlaps with s, and we attempt to strengthen s in order to excise that region from the candidate interpolant.

4.4 Theoretical Properties of bitp

We now discuss soundness and completeness of bitp. Observe that calling $\textsc {{bitp}}$ in line 5 may require further recursive calls if no $\mathcal {L}_\exists$ interpolant exists for $(s \wedge B, s \wedge A)$—i.e., the interpolant for $(s \wedge B, s \wedge A)$ is still in $\mathcal {L}_{\textsc {{af}}}$. If these recursive calls never terminate by finding an $\mathcal {L}_\exists$ interpolant at some depth, then the algorithm produces an infinite sequence of models (at least one per recursive call). We can show that the existence of such an infinite sequence is the exact criterion to determine that no $\mathcal {L}_{\textsc {{af}}}$ interpolant exists for (A, B). Accordingly, we prove the relative completeness of $\textsc {{bitp}}$—that when an $\mathcal {L}_{\textsc {{af}}}$ interpolant exists, the algorithm terminates with such an interpolant.

The following lemma states the conditions required to show that the no $\mathcal {L}_{\textsc {{af}}}$ interpolant exists for a pair of formulas (A, B).

Lemma 2

(Non-existence of $\mathcal {L}_{\textsc {{af}}}$ interpolants). Let $A, B \in \mathcal {L}$, and suppose there is an infinite alternating chain of models of A and B: $m_1^A, m_2^B, m_3^A, m_4^B, \ldots$ with the three properties

• $m_i^A \models A \text{ and } m_j^B \models B \text {, for all odd } i \text { and even } j$

• $diag (m_1^A) \Leftarrow diag (m_2^B) \Leftarrow diag (m_3^A) \Leftarrow \ldots$

• $|m_1^A|< |m_2^B|< |m_3^A| < \ldots$

Then, there is no $\mathcal {L}_{\textsc {{af}}}$ interpolant for (A, B).

Proof

We will prove this lemma by showing that for every formula $\varphi \in \mathcal {L}_{\textsc {{af}}}$ s.t. $A \Rightarrow \varphi$, we have that $\varphi \wedge B$ is sat, thus implying that no $\mathcal {L}_{\textsc {{af}}}$ interpolant exists for (A, B). The proof relies on Theorem 1 and Corollary 2.

First, define $num(\varphi ) = n+m+c$, where $\varphi \in \mathcal {L}$ is a prenex normal form formula and c is the number of free variables in $\varphi$. We shall use |m| to denote the number of elements in the universe of a model m.

Let . That is, the set $\varPhi$ is that of all $\mathcal {L}_{\textsc {{af}}}$ formulas whose models contain $\{m_i^A\}$; thus the set of possible $\mathcal {L}_{\textsc {{af}}}$ interpolants for (A, B) is contained in $\varPhi$. Assume each $\varphi _i$ is written as a Boolean combination of universal and existential subformulas. Now, pick some $\varphi \in \varPhi$ and some model $m_i^A$ such that $|m_i^A| > num(\varphi )$.

By definition of $\varPhi$, we know that $m_i^A \models \varphi$ and $m_{i+2}^A \models \varphi$. We now show that this entails that $m_{i+1}^B \models \varphi$:

• Since the number of existentially quantified variables in $\varphi$ is less than $|m_{i}^A|$, we know that $m_i^A$ and $m_{i+2}^A$ satisfy the same existential subformulas of $\varphi$.

• Since $m_{i}^A \preceq m_{i+1}^B$, by Theorem 1, $m_{i+1}^B$ also satisfies all existential subformulas of $\varphi$.

• Since $m_{i+1}^B \preceq m_{i+2}^A$, by Corollary 2, we know that $m_{i+1}^B \models \varphi$.

Therefore there is no $\mathcal {L}_{\textsc {{af}}}$ interpolant for (A, B), since any $\mathcal {L}_{\textsc {{af}}}$ formula $I \in \varPhi$, where $A \Rightarrow I$, is such that $I \wedge B$ is sat.    $\blacksquare$

We are now ready to state bitp ’s soundness and relative completeness.

Theorem 8

(Soundness and relative completeness of BITP ). Given two formulas $A, B \in \mathcal {L}$, where $A \wedge B$ is unsat,

• 1. if $\textsc {{bitp}} (A,B)$ returns a formula, then it is an interpolant of (A, B);

• 2. if A and B have an $\mathcal {L}_{\textsc {{af}}}$ interpolant, then $\textsc {{bitp}} (A,B)$ returns a formula and terminates.

Proof

If $\textsc {{bitp}}$ returns an interpolant, then it is correct by construction.

We will prove relative completeness (point 2 in theorem statement) by the contrapositive: If $\textsc {{bitp}} (A,B)$ does not terminate, then there is no $\mathcal {L}_{\textsc {{af}}}$ interpolant for (A, B). For the purposes of the proof, let us assume that the algorithm always samples a model of the smallest cardinality possible. Now, suppose that the algorithm does not terminate. This could happen in two places:

• 1. the loop (line 3) in some recursion depth d executes indefinitely, or

• 2. there is an infinite chain of recursive calls to bitp.

Case 1: We first show that case 1 is impossible. Suppose that at recursive depth d the algorithm is called on $(A',B')$. Suppose the loop does not terminate. Since models are sampled in increasing cardinality, at some point the variable I is of the form

$$ I \equiv \bigvee _{m \models A' \text { and } |m| \leqslant num(A')} diag (m) \wedge \lnot \textsc {{bitp}} (diag (m) \wedge B', diag (m) \wedge A')$$

In other words, at some point during the assumed infinite execution of the loop, the variable I will contain all diagrams of models of size $\leqslant num(A')$ (and any required strengthening). Since the loop keeps executing beyond this point, this means there is a model m s.t. $m \models A'$ and $m \not \models I$. But since $|m| > num(A')$, this means that there is a substructure $m' \preceq m$, where $m' \models A$, $|m'| \leqslant num(A)$, and $diag (m) \Rightarrow diag (m')$. But since $m' \models I$, it is also true that $m \models I$. By contradiction, the loop terminates.

Case 2: Now, consider case 2. Suppose there is an infinite chain of recursive calls. By definition of $\textsc {{bitp}}$, there is an infinite sequence of models (samples) $m_1^A$, $m_2^B$, $m_3^A$, $m_4^B, \ldots$ such that

$$\begin{aligned}&diag (m_1^A) \Leftarrow diag (m_2^B) \Leftarrow diag (m_3^A) \Leftarrow \ldots \end{aligned}$$

(3)

$$\begin{aligned}&|m_1^A|< |m_2^B|< |m_3^A| < \ldots \end{aligned}$$

(4)

$$\begin{aligned}&\text {for all } m_i^X, diag (m_i^X)\wedge A \text { is } \textsc {{sat}} \text { and } diag (m_i^X)\wedge B \text { is } \textsc {{sat}} \end{aligned}$$

(5)

This happens by construction due to the alternation of $\textsc {{bitp}}$: in the first recursive call, it conjoins $diag (m_1^A)$ to A and B; then, in the second recursive call, $diag (m_2^B)$ is conjoined to A and B, where $m_2^B \models diag (m_1^A)$, etc. As a result, we get constraint 3. Constraint 4 is implied by the fact that $A \wedge B$ is unsat. (If there is i such that $|m_i^A| = |m_{i+1}^B|$ or $|m_i^B| = |m_{i+1}^A|$ this means that A and B have the same model.) Constraint 5 is implied by the fact that the sequence is infinite.

Following Lemma 2, non-termination means there is no $\mathcal {L}_{\textsc {{af}}}$ interpolant.   $\blacksquare$

Fig. 4.

Illustration of an infinite, alternating sequence of models satisfying conditions of Lemma 2, where and

4.5 bitp Examples

The following example illustrates a successful run of $\textsc {{bitp}}$.

Example 2

Consider the following formulas, and suppose we call $\textsc {{bitp}}$ on (A, B).

Initially, $S = \emptyset$ and the candidate interpolant $\bigvee S \equiv false$. So, we start by sampling (line 8) the model m with the following diagram, . In the next iteration around the loop, we will notice that $s_m \wedge B$ is sat (line 4); therefore, we call $\textsc {{uitp}}$ on $(s_m \wedge B, s_m \wedge A)$. The result we get is the following: . As shown in line 6, we now strengthen $s_m$ by setting it to $s_m \wedge \lnot I$. At this point, $s_m$ is an interpolant, and therefore the algorithm terminates.    $\blacksquare$

We now demonstrate bitp on an example with no $\mathcal {L}_{\textsc {{af}}}$ interpolant.

Example 3

We use the same example as in Sect. 2:

bitp might begin by sampling the model $m_1^A$ of A with Model $m_1^A$ is shown pictorially on the left side of Fig. 4. bitp now recursively looks for an interpolant of $(B \wedge diag (m_1^A), A \wedge diag (m_1^A))$.

At this point, bitp samples from $B \wedge diag (m_1^A)$ the model $m_2^B$ of cardinality 2 with the diagram:

Note that $diag (m_2^B) \wedge (A \wedge diag (m_1^A))$ is still satisfiable, so $\textsc {{bitp}}$ will make yet another recursive call to $(A \wedge diag (m_1^A) \wedge diag (m_2^B), B \wedge diag (m_1^A) \wedge diag (m_2^B))$. We will notice that the cardinality of sampled models keeps increasing as $\textsc {{bitp}}$ continues to run, and in fact, $\textsc {{bitp}}$ will never terminate, since there is no $\mathcal {L}_{\textsc {{af}}}$ interpolant for (A, B).

Specifically, bitp will end up constructing an infinite alternating sequence of models $m_1^A, m_2^B, m_3^A, m_4^B,\ldots$. A possible infinite alternating sequence of models of A and B is illustrated in Fig. 4. Observe that this sequence satisfies the conditions of Lemma 2 for non-existence of an $\mathcal {L}_{\textsc {{af}}}$ interpolant.    $\blacksquare$

5 Implementation and Evaluation

Implementation. We have implemented prototypes of uitp and bitp using the Z3 smt solver [20] as a black box. To evaluate the performance and utility of our algorithms, we built a simple interpolation-based verifier, itpv, for transition systems in epr. itpv expects a transition system $TS = (init , trans , bad )$. itpv unrolls the transition relation and uses our interpolation algorithms to compute interpolants and discover a safe inductive invariant for $TS$.

Evaluation. We applied itpv on singly- and doubly-linked-list benchmarks [15, 17]. We compared the performance of itpv against two tools: (i) pdr $_\alpha$ [15], a predicate-abstraction-based verifier based on property-directed reachability (pdr), and (ii) pdr $_\forall$ [17], a pdr-based verifier that uses diagrams for generalizing counterexamples. To our knowledge, these are the only two other techniques for automated verification of programs encoded in epr. Note, however, that both pdr $_\alpha$ and pdr $_\forall$ can only compute universally-quantified invariants (in $\mathcal {L}_\forall$). We considered a set of benchmarks that require $\mathcal {L}_\forall$ invariants, and another a set that require $\mathcal {L}_{\textsc {{af}}}$ invariants, as detailed below.

Table 1. Experimental results: (a) $\mathcal {L}_\forall$ benchmarks and (b) $\mathcal {L}_{\textsc {{af}}}$ benchmarks

Universal Proofs. Table 1(a) shows the results of applying itpv, pdr $_\alpha$, and pdr $_\forall$ to proving memory safety of a set of list-manipulating benchmarks drawn from [15, 17].¹ All of these benchmarks require inductive invariants in $\mathcal {L}_\forall$. The symbol ✗$_t$ indicates that the tool did not return a solution within a 10 min time limit, and ✗$_\alpha$ indicates that the predicate abstract domain of pdr $_\alpha$ is not precise enough to compute a safe inductive invariant. Column D indicates the depth of the unrolling (pdr frames or transition relation unrollings) an algorithm required to compute a safe inductive invariant.

Our results primarily indicate that our interpolation technique (i) is a viable means for verifying non-trivial epr transition relations and (ii) results in a verification tool that is comparable to the state-of-the-art in epr verification. Digging deeper into the results, we see that itpv is almost consistently superior to pdr $_\alpha$. Compared to pdr $_\forall$, we witness comparable performance. On benchmarks 8 and 15, however, we observe that itpv is slower than pdr $_\forall$. We discovered that this occurs when one needs to interpolate over a deep unrolling of the transition relation in order to find an inductive invariant (on these examples, D is 6 and 7). This is an artifact of two factors: (i) the satisfiability algorithm in Z3 and (ii) the algorithmic differences between interpolation-based verification and property-directed reachability. pdr techniques do not explicitly unroll the transition relation, and therefore tend to make more but smaller sat queries. Interpolation techniques unroll the transition relation, resulting in large sat queries. The performance of the epr satisfiability procedure in Z3 suffers when we give it large formulas, leading to slower verification when deep unrollings are needed. We thus hope that the benchmarks generated through this work would influence the design of more efficient epr satisfiability procedures; for instance, linear orders [14, 17, 21] can benefit from specialized quantifier instantiation that exploits their transitivity and antisymmetry [6].

Alternating Proofs. Table 1(b) shows a set of benchmarks requiring inductive invariants in $\mathcal {L}_{\textsc {{af}}}$. The first two benchmarks are from [17], where it is shown that pdr $_\forall$ declares that no universally-quantified invariant exists. The rest of the benchmarks are modifications of the ones appearing in Table 1(a), where we manually modified the program to require existential as well as universal quantifiers in the proof. To our knowledge, itpv is the first tool to be able to automatically compute inductive invariants over the rich class of $\mathcal {L}_{\textsc {{af}}}$ formulas.

6 Related Work

Interpolation and EPR. Our algorithm is inspired by the recent model-based interpolation techniques that rely on sampling models of A and B to construct a simple interpolant [2, 28]. Thus far these techniques have been limited to linear arithmetic. Whereas our work here also constructs an interpolant by generalizing from models, the underlying methodology is very different.

The line of work by Itzhaky et al. [13–15] and Karbyshev et al. [17] showed us how to encode linear data structures in epr. The model generalization technique our algorithm uses is similar to the notion of diagrams used in the recent property-directed reachability [8] algorithm for epr [17]. Our interpolation technique enables construction of both universal, existential, and mixed quantifier interpolants—and therefore invariants. This is in contrast to existing verification techniques that only compute universal invariants. Additionally, the notion of interpolants is general and of independent interest outside of safety checking.

Another close work to ours is that of Bjørner et al. [7]: in a short paper, the authors sketch out a model-based epr interpolation algorithm. However, unlike our work, it does not guarantee that the interpolants are alternation-free. There are also a number of works on interpolation techniques for arrays and heap-manipulating programs [1, 3, 16, 31]. Our work differs in that it targets the epr fragment of first-order logic, which none of those works apply to.

Symbolic Abstraction. Our work has connections with symbolic abstraction [27], in which a formula in a rich logic is abstracted into one that subsumes it in a weaker logic. The approach of Reps et al. [27] performs this abstraction by sampling models and growing the abstraction starting from bottom. Thakur defined the notion of abstract interpolants [30], which are interpolants in a restricted logic, and showed how to use symbolic abstraction to compute them. Our techniques can be viewed through this lens, as we restrict interpolants to a sub-fragment of epr and iteratively grow interpolants. Another work in the same vein is that on learning quantified data automata [11] for verifying linear data structures. The similarity between our works is that both use a black box teacher to learn quantified invariants. Our technique, however, can compute invariants with combinations of quantifiers, and operates in the setting of epr.