Transitivity and Difunctionality of Bisimulations

Abstract

Bisimilarity and observational equivalence are notions that agree in many classical models of coalgebras, such as e.g. Kripke structures. In the general category $Set_{F}$ of $F-$coalgebras these notions may, however, diverge. In many cases, observational equivalence, being transitive, turns out to be more useful.

In this paper, we shall investigate the role of transitivity for the largest bisimulation of a coalgebra. Passing to relations between two coalgebras, we choose difunctionality as generalization of transitivity. Since in $Set_{F}$ bisimulations are known to coincide with $\bar{F}-$simulations, we are led to study the notion of $L-$similarity, where L is a relation lifting.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In the 1990s, J. Rutten developed a universal theory for state-based systems. Such systems were represented as coalgebras in [19]. A coalgebra of type F is a pair consisting of a base set A and a structure map $\alpha :A\longrightarrow F(A)$ where F is any Set-endofunctor. Many of the early structural results, we just exemplarily mention [16], assumed that the type functor F should preserve weak pullbacks. In [5], one of the present authors began studying the role of weak pullback preservation. In [4, 14] he extended many results from [19] to the case of arbitrary functors, adding new coalgebraic constructions, e.g. for building terminal coalgebras. A systematic study relating preservation properties of functors to structural (coalgebraic) properties of their coalgebras was given in [8]. In particular, preservation properties were related to properties of bisimulations and congruences. For instance, it was shown that bisimulations restrict to subcoalgebras, if and only if the functor F preserves preimages, i.e. pullbacks along regular monos.

Bisimulations, as compatible relations have been introduced by Aczel and Mendler in [1]. An alternative definition, equivalent for Set-coalgebras was given by Hermida and Jacobs [13].

A concept, competing with bisimulations is the notion of a congruence relation $\theta$ as a kernel $\text {ker}\,\varphi$ of a homomorphism $\varphi$. Just as there is always a largest bisimulation $\sim _{\mathcal {A}}$, there is also a largest congruence $\nabla _{\mathcal {A}}$ on every coalgebra $\mathcal {A}$. The disadvantage of $\sim _{\mathcal {A}}$ versus $\nabla _{\mathcal {A}}$ is, that even though $\sim _{\mathcal {A}}$ is reflexive and symmetric, it need not be transitive, hence it is not able to reflect logical equivalence. Since the equivalence hull of any bisimulation is always a congruence relation [1], we have the implications

$$\begin{aligned} \sim _{\mathcal {A}}\subseteq \sim _{\mathcal {A}}^{*}\subseteq \nabla _{\mathcal {A}} \end{aligned}$$

where each of the inclusions may be strict.

Already in [1], bisimulations were defined as relations between two (possible different) coalgebras $\mathcal {A}$ and $\mathcal {B}$. The notion of congruence can as easily be extended to the notion of 2-congruence, defined as the kernel of a sink of two homomorphisms $\varphi :\mathcal {A}\rightarrow \mathcal {C}$, and $\psi :\mathcal {B}\rightarrow {\mathcal {C}}$ i.e. as $\text {ker}(\varphi ,\psi ):=\{(a,b)\mid \varphi (a)=\psi (b)\}$. (2-congruences were studied by S. Staton [21] under the name of kernel-bisimulations. However they are not necessarily bisimulations in the original sense, so we prefer to call them 2-simulations). Again, for the case of two coalgebras $\mathcal {A}$ and $\mathcal {B}$ it is easy to see that there is again a largest bisimulation $\sim _{\mathcal {A},\mathcal {B}}$ as well as a largest 2-congruence $\nabla _{\mathcal {A},\mathcal {B}}$. The above inequalities do not immediately generalize, since transitivity makes no sense for relations between different sets. An alternative notion, however, is difunctionality as introduced by Riguet [18]. The inequality corresponding to the above is then

$$\begin{aligned} \sim _{\mathcal {A},\mathcal {B}}\subseteq \sim _{\mathcal {A},\mathcal {B}}^{d}\subseteq \nabla _{\mathcal {A},\mathcal {B}} \end{aligned}$$

where $R^{d}$ denotes the difunctional closure of a relation R.

The definition of bisimulation given by Hermida and Jacobs used the fact that a relation $R\subseteq A\times B$ can easily be lifted to a relation $\bar{F}R\subseteq F(A)\times F(B)$, often called the Barr extension of R. Generalizing this to an arbitrary relation lifting L leads to the notion of $L-$simulation as studied by Thijs [22] and in a series of papers by Venema et al., see e.g. [15].

The congruences which can be obtained as transitive closure of bisimulations are exactly the regular congruences i.e. kernels of coequalizers [8]. In the same paper it was shown that a functor F preserves weak kernel pairs if and only every congruence on a single coalgebra in $Set_{F}$ is a bisimulation. In the present paper, which subsumes some results obtained in the first author’s Master thesis [24], we want to explain further the relationship between bisimulations and $2-$congruences and, assuming a monotonic relation lifting L, we study the difunctional closure of $L-$similarity. A quite useful tool is provided by a result, giving conditions for a bisimulation to restrict to subcoalgebras without assuming anything about the functor F.

2 Basic Notions

For a product $A\times B$ we denote the projections to the components by $\pi _{A}$ and $\pi _{B}$. Given a relation $R\subseteq A\times B$, the restrictions to R of the projections are $\pi _{A}^{R}:=\pi _{A}\circ \iota _{R}$ where $\iota _{R}:R\hookrightarrow A\times B$ is set inclusion. Given a second relation S with $R\subseteq S\subseteq A\times B$ we note that $\pi _{A}^{R}=\pi _{A}^{S}\circ \iota _{R}^{S}$, where $\iota _{R}^{S}:R\hookrightarrow S$ is, again, the inclusion map.

The converse of a relation R is $R^{-}:=\{(b,a)\mid (a,b)\in R\}$. For a subset $U\subseteq A$, we let $R[U]:=\{b\in B\mid \exists u\in U.(u,b)\in R\}$. A relation $R\subseteq A\times A$ is transitive if for all $x,y,z\in A$ we have $(x,y),(y,z)\in R\implies (x,z)\in R.$ Equivalently, R is transitive, if $R\circ R\subseteq R$ where $\circ$ is relational composition. The reflexive transitive closure of R is called $R^{\star }$.

Transitivity makes no sense for relations $R\subseteq A\times B$ between different sets, sodifunctionality [18] can be considered as a possible generalization of transitivity:

Definition 1

A relation $R\subseteq A\times B$ is called difunctional, if for all $a_{1},a_{2}\in A$ and for all $b_{1},b_{2}\in B$ it satisfies:

$$\begin{aligned} (a_{1},b_{1}),(a_{2},b_{1}),(a_{2},b_{2})\in R\implies (a_{1},b_{2})\in R. \end{aligned}$$

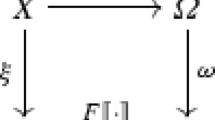
This notion can be illustrated by the following figure, which explains why “difunctional” is sometimes called “z-closed”:

It is elementary to see that the difunctional closure of a relation R is

$$\begin{aligned} R^{d}:=R\circ (R^{-}\circ R)^{\star }=(R\circ R^{-})^{\star }\circ R \end{aligned}$$

where $R^{-}$ is the converse relation to R. The difunctional closure can also be obtained as the pullback of the pushout of $\pi _{A}^{R}$ with $\pi _{B}^{R}$ [9, 18].

2.1 Categorical Notions

We assume only elementary categorical notions and we use the terminology of [2]. Regular monos are equalizers of a parallel pair of morphisms. Analogously, regular epis are coequalizers. Split epis (split monos) i.e. the right-(left-)-invertible morphisms are regular epi (regular mono). We denote the sum of a family $(A_{i})_{i\in I}$ of objects and with the canonical injections by $e_{A_{i}}:A_{i}\rightarrow \Sigma _{i\in I}A_{i}$. Given a sink $(q_{i}:A_{i}\longrightarrow Q)_{i\in I}$ we denote the induced morphisms from the sum $\sum A_{i}\rightarrow Q$ by $[(q_{i})_{i\in I}]$. The following lemma will be needed later. It is obviously true in every category with sums:

Lemma 1

For all morphisms $f:A\longrightarrow B$ the map $[f,id_{B}]:A+B\rightarrow B$ is split epi.

Definition 2

A weak limit of a diagram D is a cone over D such that for every other (competing) cone there is at least one morphism making the relevant triangles commutative.

If we replace “at least one” in the above definition with “exactly one”, this is the definition of limit.

Set -Endofunctors. In the following, F will always be a Set-endofunctor. F preserves epis, and F preserves monos with nonempty domain. Next, let D a diagram.

Definition 3

F weakly preserves D-limits if F maps every D-limit into a weak D-limit.

It is well known that F weakly preserves D-limits if and only if it preserves weak D-limits, see [5].

An important property of Set-endofunctors is that they preserve finite nonempty intersections [23]. In order to preserve all finite intersections, it might be necessary to redefine F on the empty set and on empty mappings to obtain a (marginally modified) new functor preserving all finite intersections. Therefore, we are safe to only consider functors which preserve all finite intersections.

2.2 F-coalgebras

Definition 4

Let $F:Set\rightarrow Set$ be a Set-endofunctor. An F-coalgebra $\mathcal {A}=(A,\alpha )$ consists of a set A and a structure map $\alpha :A\rightarrow F(A).$ A map $\varphi :A\rightarrow B$ between two coalgebras $\mathcal {A}=(A,\alpha )$ and $\mathcal {B}=(B,\beta )$ is called a homomorphism, if $\beta \circ \varphi =F\varphi \circ \alpha$. A subcoalgebra of a coalgebra $\mathcal {A}$ is a subset $U\subseteq A$ with a structure map $\alpha _{U}$ such that the inclusion map $\iota _{U}^{X}:U\hookrightarrow X$ is a homomorphism.

The class of all $F-$coalgebras with coalgebra homomorphisms forms the category $Set_{F}$. In [3] it is proved that $Set_{F}$ is cocomplete i.e. every colimit exists. Epis are exactly the surjective homomorphisms [19]. Monomorphisms in $Set_{F}$ need not be injective. Regular monos are exactly the injective homomorphisms [6].

Bisimulations

Definition 5

(Aczel and Mendler [1]). A bisimulation between two coalgebras $\mathcal {A}$ and $\mathcal {B}$ is a relation $R\subseteq A\times B$ for which there exists a coalgebra structure $\rho :R\rightarrow F(R)$ such that the projections $\pi _{A}^{R}:R\rightarrow A$ and $\pi _{B}^{R}:R\rightarrow B$ are homomorphisms. A bisimulation R on a coalgebra $\mathcal {A}$ is a bisimulation between $\mathcal {A}$ and itself.

The union of bisimulations is a bisimulation and $\emptyset$ is always a bisimulation, so that the bisimulations between $\mathcal {A}$ and $\mathcal {B}$ form a complete lattice with largest element called $\sim _{\mathcal {A},\mathcal {B}}.$ For the same reason, every relation R between coalgebras $\mathcal {A}$ and $\mathcal {B}$ contains a largest bisimulation, which we denote by [R]. It is the union of all bisimulations contained in R.

Congruences and $2-$ congruences

Definition 6

A congruence $\theta$ on a coalgebra $\mathcal {A}$ is the kernel of a homomorphism $\varphi :\mathcal {A}\rightarrow \mathcal {C}$, i.e $\theta =\text {ker}\,\varphi =\{(a,a')\in A\times A\,|\,\varphi (a)=\varphi (a')\}$.

If $\theta$ is a congruence on $\mathcal {A}$, then there is a structure map on the factor set $A/\theta :=\{[a]\theta \,|\,a\in A\}$, such that $\pi _{\theta }:\mathcal {A}\longrightarrow A/\theta$ with $\pi _{\theta }(a):=[a]\theta :=\{a'\in A\mid a\theta a'\}$ becomes a homomorphism. The set of all congruences on a coalgebra $\mathcal {A}$ forms a complete lattice [7] with largest element called $\nabla _{\mathcal {A}}$ and smallest element $\varDelta _{A}=\{(a,a)\mid a\in A\}.$ The supremum of a family of congruences is obtained as the transitive closure of their union. We denote the lattice of all congruences by $Con(\mathcal {A}).$

Given a bisimulation R on $\mathcal {A}$, its equivalential hull, that is the smallest equivalence relation containing R is a congruence relation [1]. It follows immediately, that $\sim _{\mathcal {A}}\subseteq \nabla _{\mathcal {A}}$. Congruences arising as equivalential hulls of a bisimulation are called regular. This notion is suggested by the following result from [8]:

Lemma 2

A morphism $\varphi :\mathcal {A}\rightarrow {\mathcal {B}}$ is mono iff $[\text {ker}\varphi ]=\varDelta _{A}$ and regular mono, iff it is injective.

An epi $\varphi :\mathcal {A}\twoheadrightarrow {\mathcal {B}}$ is regular epi (in $Set_{F}$) iff its kernel is a regular congruence iff $\text {ker}\varphi =[\text {ker}\varphi ]^{\star }.$

For technical reasons, we call a homomorphism $\varphi$ strictly regular, if its kernel is a bisimulation, i.e. if $\text {ker}\varphi =[\text {ker}\varphi ].$ Notice that this notion is not an abstract categorical one, but a coalgebraic notion.

Definition 7

A $2-$ congruence between two coalgebras $\mathcal {A}$ and $\mathcal {B}$ is the kernel (pullback in the category Set) of two homomorphisms $\varphi :\mathcal {A}\rightarrow \mathcal {C}$ and $\psi :\mathcal {B}\rightarrow \mathcal {C}$, i.e.

$$\begin{aligned} \theta =\text {ker}(\varphi ,\psi ):=\{(a,b)\in A\times B\,|\,\varphi (a)=\psi (b)\}. \end{aligned}$$

Just as congruences are transitive, $2-$congruences are difunctional. The largest $2-$congruence between $\mathcal {A}$ and $\mathcal {B}$ is called observational equivalence and written $\nabla _{\mathcal {A},\mathcal {B}}$. For each bisimulation R between $\mathcal {A}$ and $\mathcal {B}$, its difunctional hull $R^{d}$, being the kernel of the pushout of the components $\pi _{\mathcal {A}}^{R}$ and $\pi _{\mathcal {B}}^{R}$ is a 2-congruence, so $R^{d}\subseteq \nabla _{\mathcal {A},\mathcal {B}}.$

3 Observational Equivalence and Bisimilarity

When $\mathcal {A}$ and $\mathcal {B}$ are coalgebras, elements $a\in \mathcal {A}$ and $b\in \mathcal {B}$ are called bisimilar, if there exists a bisimulation R between $\mathcal {A}$ and $\mathcal {B}$ containing (a, b). This is the same as saying that for some coalgebra $\mathcal {R}$ and homomorphisms $\varphi _{\mathcal {A}}:\mathcal {R}\rightarrow \mathcal {A}$ and $\varphi _{\mathcal {B}}:\mathcal {R}\rightarrow \mathcal {B}$ there is some $r\in \mathcal {R}$ with $\varphi _{\mathcal {A}}(r)=a$ and $\varphi _{\mathcal {B}}(r)=b.$ In short, a and b are bisimilar, if they have a common ancestor.

Dually, a and b are called observationally equivalent, iff they have a common offspring, meaning that there exists a coalgebra $\mathcal {C}$ and homomorphisms $\psi _{\mathcal {A}}:\mathcal {A}\rightarrow \mathcal {C}$ and $\psi _{\mathcal {B}}:\mathcal {B}\rightarrow \mathcal {C}$ with $\psi _{\mathcal {A}}(a)=\psi _{\mathcal {B}}(b)$. We first study the situation for the case $\mathcal {A}=\mathcal {B}$. Here $a,\,a'$ are bisimilar iff $(a,a')\in \sim _{\mathcal {A}}$ and observationally equivalent iff $(a,a')\in \nabla _{\mathcal {A}}.$

3.1 Nabla and Simple Coalgebras

Definition 8

A coalgebra $\mathcal {A}$ is called simple, if $\nabla _{\mathcal {A}}=\varDelta _{\mathcal {A}}$ and extensional, if $\sim _{\mathcal {A}}=\varDelta _{\mathcal {A}}$.

It is well known that a coalgebra $\mathcal {A}$ is simple iff each morphism starting in $\mathcal {A}$ is injective [4]. If a terminal coalgebra $\mathcal {T}$ exists, simple coalgebras are precisely the subcoalgebras of $\mathcal {T}$ [4]. For every coalgebra $\mathcal {A},$ the factor coalgebra $\mathcal {A}/\nabla _{\mathcal {A}}$ is simple. The notions of simplicity and extensionality differ [7]. The coalgebra of the following example is extensional but not simple.

Example 1

Consider the above $2\times \mathbb {P}_{\le 3}-$coalgebra $\mathcal {A}:=(\{0,1,2,3\},\alpha )$ with $\alpha (0):=(0,\{0,1,2\}),\alpha (2):=(1,\{0,1,2\}),$ $\alpha (1)=(0,\{1,2,3\}),\alpha (3)=(1,\{1,2,3\}).$ It is easy to check that $\nabla =\{(0,1),(1,0),(2,3),(3,2)\}\cup \varDelta _{A}$. Suppose that $(0,1)\in \sim .$ Then there is $(0,M)\in 2\times \mathbb {P}_{\le 3}\sim$ with $\pi _{1}[M]=(0,1,2)$ and $\pi _{2}[M]=(1,2,3).$ Hence $M=\{(0,1),(1,1),(2,2),(2,3)\}$. This is a contradiction, because $|M|=4$. Similarly $(2,3)\not \in \,\sim$. We obtain $\sim \,=\varDelta \ne \nabla$.

The following lemma helps us to verify whether a congruence $\theta$ is the largest congruence. It suffices to check that the codomain of a factor is simple.

Lemma 3

Subcoalgebras of simple coalgebras are simple. More generally, if $\varphi :\mathcal {A}\rightarrow \mathcal {C}$ is a homomorphism and $\mathcal {C}$ is simple, then $\ker \varphi =\nabla _{\mathcal {A}}$.

Proof

Let $\iota :\mathcal {U}\hookrightarrow \mathcal {C}$ be the inclusion morphism, and assume that $\theta$ is a congruence on $\mathcal {U}$. The pushout of $\iota$ with $\pi _{\theta }$ yields a homomorphism $\psi :\mathcal {C}\rightarrow \mathcal {P}$. Since $\mathcal {C}$ is simple, $\psi$ is injective. It follows that $\pi _{\theta }$ is injective. This means that $\nabla _{\mathcal {U}}=\varDelta _{U}$. Next, let $\varphi :\mathcal {A}\rightarrow \mathcal {C}$ be a homomorphism and C simple. The image of $\mathcal {A}$ under $\varphi$ is a subcoalgebra of $\mathcal {C}$, which, as we have just seen, must be simple. Thus we may as well assume that $\varphi$ is epi. Obviously, $\ker \varphi \subseteq \nabla _{\mathcal {A}}$, so there is a homomorphism $\psi :\mathcal {C}\rightarrow \mathcal {A}/\nabla _{\mathcal {A}}$ with $\pi _{\nabla _{\mathcal {A}}}=\psi \circ \varphi .$ So $\psi$ is surjective, and injective, since $\mathcal {C}$ is simple. It follows that $\psi$ is an isomorphism, whence $\ker \varphi =\ker \pi _{\nabla _{\mathcal {A}}}=\nabla _{\mathcal {A}}.$

The following lemma relates observational equivalence between two coalgebras to observational equivalence on their sum:

Lemma 4

[14] $(a,b)\in \nabla _{\mathcal {A},\mathcal {B}}\iff (e_{A}(a),e_{B}(b))\in \nabla _{\mathcal {A}+\mathcal {B}}.$

Proof

$$\begin{aligned} (a,b)\in \nabla _{\mathcal {A},\mathcal {B}}\iff & {} \exists \mathcal {C},\varphi :\mathcal {A}\rightarrow \mathcal {C},\psi :\mathcal {B}\rightarrow \mathcal {C}.\,\varphi (a)=\psi (b)\\\iff & {} \exists \mathcal {C},\chi :\mathcal {A}+\mathcal {B}\rightarrow \mathcal {C},\,\chi (e_{\mathcal {A}}(a))=\chi (e_{\mathcal {B}}(b))\\\iff & {} (e_{A}(a),e_{B}(b))\in \nabla _{\mathcal {A}+\mathcal {B}}. \end{aligned}$$

We need to extend Lemma 3 to the case of a cospan of two homomorphisms:

Lemma 5

If $\varphi :\mathcal {A}\rightarrow \mathcal {C}$ and $\psi :\mathcal {B}\rightarrow \mathcal {C}$ are homomorphism and $\mathcal {C}$ is simple, then $\ker (\varphi ,\psi )=\nabla _{\mathcal {A},\mathcal {B}}$.

Proof

Consider $[\varphi ,\psi ]:\mathcal {A}+\mathcal {B}\rightarrow \mathcal {C}$ with $\varphi =[\varphi ,\psi ]\circ e_{\mathcal {A}}$ and $\psi =[\varphi ,\psi ]\circ e_{\mathcal {B}}$. By Lemma 3, we obtain $\ker [\varphi ,\psi ]=\nabla _{\mathcal {A}+\mathcal {B}}$, so with this and Lemma 4 we calculate:

$$\begin{aligned} \varphi (a)=\psi (b)\iff & {} [\varphi ,\psi ]\circ e_{\mathcal {A}}(a)=[\varphi ,\psi ]\circ e_{\mathcal {B}}(b)\\\iff & {} (e_{\mathcal {A}}(a),e_{\mathcal {B}}(b))\in \ker [\varphi ,\psi ]\\\iff & {} (e_{\mathcal {A}}(a),e_{\mathcal {B}}(b))\in \nabla _{\mathcal {A}+\mathcal {B}}\\\iff & {} (a,b)\in \nabla _{\mathcal {A},\mathcal {B}}. \end{aligned}$$

The following construction will be used in various places. It can be used to change the structure map $\alpha$ of a coalgebra while at the same time preserving other important properties as seen in the ensuing lemma:

Definition 9

Given a coalgebra $\mathcal {A}=(A,\alpha )$, element $x_{0}\in A$ and subset $U\subseteq A$. We define a new coalgebra $\mathcal {A}_{x_{0}}^{U}:=(A,\bar{\alpha })$ on the same base set by constantly mapping all elements of U to $\alpha (x_{0})$ and retaining $\alpha$ on all other elements, i.e.:

$$\begin{aligned} \bar{\alpha }(x):={\left\{ \begin{array}{ll} \alpha (x_{0}) &{} if\,x\in U\\ \alpha (x) &{} else. \end{array}\right. } \end{aligned}$$

Lemma 6

Let $\varphi :\mathcal {A}\rightarrow {\mathcal {C}}$ be a homomorphism and $U\subseteq [x_{0}]\ker \varphi$ for some $x_{0}\in A$. Then the map $\varphi :A\rightarrow C$ is also a homomorphism $\varphi :\bar{\mathcal {A}}\mathcal {\rightarrow \mathcal {C}}$ where $\mathcal {\bar{A}}:=\mathcal {A}_{x_{0}}^{U}.$ Moreover, $\nabla _{\mathcal {A}}=\nabla _{\mathcal {\bar{A}}}$.

Proof

If $x\in U,$ then $(F\varphi \circ \bar{\alpha })(x)=(F\varphi )(\alpha _{\mathcal {A}}(x_{0}))=\alpha _{\mathcal {C}}(\varphi (x_{0}))=\alpha _{\mathcal {C}}(\varphi (x)).$ If $x\notin U$, nothing has changed, so $\varphi$ keeps being a homomorphism. With $\mathcal {C}=A/\nabla _{\mathcal {A}}$ and Lemma 3, we obtain $\nabla _{\mathcal {A}}=\ker \varphi =\nabla _{\bar{\mathcal {A}}}$.

3.2 Restricting Bisimulations

For the following we assume that $R\subseteq A_{1}\times A_{2}$ is a bisimulation between coalgebras $\mathcal {A}_{1}=(A,\alpha _{1})$ and $\mathcal {A}_{2}=(A,\alpha _{2})$, and $\mathcal {U}_{i}\le \mathcal {A}_{i}$ are subcoalgebras for $i=1,2.$

Definition 10

R restricts to $U:=U_{1}\times U_{2}$, if $R\upharpoonright U:=R\cap (U_{1}\times U_{2})$ is a bisimulation between $\mathcal {U}_{1}$ and $\mathcal {U}_{2}$.

Without any further assumption, bisimulations will not necessarily restrict to subcoalgebras. In fact in [6] it was shown that all bisimulations restrict to all subcoalgebras, globally throughout $Set_{F}$, if and only if F preserves preimages. In spite of this, here we can identify conditions on R and on the $U_{i}$ that guarantee that R restricts to $U_{1}\times U_{2}$ without any condition on F. The main result of this section is the following theorem and its applications:

Theorem 1

If there exist $\kappa _{i}:A_{i}\rightarrow U_{i}$ left inverses to the inclusion maps, satisfying for all $a_{1}\in A_{1},$ $a_{2}\in A_{2}$:

$$ (a_{1},a_{2})\in R\implies (\kappa _{1}a_{1},\kappa _{2}a_{2})\in R $$

then R restricts to U.

Instantiating the existential quantifier in this theorem with particularly natural left inverses to the inclusion maps, we shall obtain the following, easy-to-apply criterion (Here R[U] denotes $\{y\mid \exists x\in U.(x,y)\in R\}$ and $R^{-}$ is the converse relation to R):

Theorem 2

If $R[U_{1}]\subseteq U_{2}$ and $R^{-}[U_{2}]\subseteq U_{1}$ then R restricts to a bisimulation between $\mathcal {U}_{1}$ and $\mathcal {U}_{2}$.

The following further specialization with $\mathcal {U\le \mathcal {A}}$ and R a bisimulation on $\mathcal {A}$ will likely be the most useful one:

Corollary 1

A bisimulation R on $\mathcal {A}$ restricts to the subcoalgebra $\mathcal {U}\le \mathcal {A}$, provided that $R[U]\subseteq U$ and $R^{-}[U]\subseteq U$.

Given an epimorphism $\varphi :\mathcal {A}\twoheadrightarrow \mathcal {B}$, the largest bisimulation contained in its kernel reveals, whether $\varphi$ is a regular epi in the category $Set_{F}$ or not. We start with $[\text {ker}\,\varphi ]$, the largest bisimulation contained in the kernel of $\varphi .$ The criterion found in [8] is, that the transitive hull of $[\text {ker}\,\varphi ]$ should be all of $\text {ker}\,\varphi .$ Expressed as a formula this is: $[\text {ker}\,\varphi ]^{\star }=\text {ker}\,\varphi .$ Studying this further, we show the following result, which turns out to be another corollary:

Corollary 2

From $\varphi _{i}:\mathcal {A}_{i}\rightarrow \mathcal {B}_{i}$ construct $\varphi _{1}+\varphi _{2}:\mathcal {A}\rightarrow \mathcal {B}$ with $\mathcal {A}:=\mathcal {A}_{1}+\mathcal {A}_{2}$ and $\mathcal {B}:=\mathcal {B}_{1}+\mathcal {B}_{2}$. Consider $ker\,\varphi _{i}$ as subsets of A, then $[\text {ker}\,(\varphi _{1}+\varphi _{2})]=[\text {ker}\,\varphi _{1}]\cup [\text {ker}\,\varphi _{2}]$.

To see why this follows from Corollary 1, choose $\mathcal {U}_{i}:=\mathcal {A}_{i}\le \mathcal {A}$: If $R\subseteq \text {ker}\,(\varphi _{1}+\varphi _{2})$ is a bisimulation, then $R[A_{i}]\subseteq \text {ker}\,(\varphi _{1}+\varphi _{2})[A_{i}]=A_{i}$ and symmetrically $R^{-}[A_{i}]\subseteq A_{i}$. Thus R restricts to $A_{i}\subseteq A_{1}+A_{2}.$ This proves that $[\text {ker}\,(\varphi _{1}+\varphi _{2})]\subseteq [\text {ker}\,\varphi _{1}]\cup [\text {ker}\,\varphi _{2}]$. The other direction is trivial, since $\text {ker}\varphi _{i}\subseteq \text {ker}(\varphi _{1}+\varphi _{2})$, hence $[\text {ker}\varphi _{i}]\subseteq [\text {ker}(\varphi _{1}+\varphi _{2})]$.

We now turn to the proof of Theorem 1:

Proof

(of Theorems 1 and 2 ). Consider the following diagram, where we use $\iota$, possibly with indices, to denote inclusion maps and similarly $\pi _{i}$ or $\bar{\pi }_{i}$ to denote projection maps to the i-th component, for $i=1,2.$ The $\kappa _{i}$ are the mentioned left inverses to the $\iota _{i}$ and $\kappa :=\kappa _{1}\times \kappa _{2}$. The condition of the theorem guarantees that $\kappa 's$ codomain is indeed $R\upharpoonright U$, and by definition, we have:

$$\begin{aligned} \bar{\pi }_{i}\circ \kappa =\kappa _{i}\circ \pi _{i}. \end{aligned}$$

Simply define

$$\begin{aligned} \bar{\rho }:=F(\kappa )\circ \rho \circ \iota \end{aligned}$$

and chase the following diagram:

$$\begin{aligned} F\bar{\pi }_{i}\circ \bar{\rho }= & {} F\bar{\pi }_{i}\circ F\kappa \circ \rho \circ \iota \\= & {} F\kappa _{i}\circ F\pi _{i}\circ \rho \circ \iota \\= & {} F\kappa _{i}\circ \alpha _{A_{i}}\circ \pi _{i}\circ \iota \\= & {} F\kappa _{i}\circ \alpha _{A_{i}}\circ \iota _{i}\circ \bar{\pi }_{i}\\= & {} F\kappa _{i}\circ F\iota _{i}\circ \alpha _{U_{i}}\circ \bar{\pi }_{i}\\= & {} Fid_{A_{i}}\circ \alpha _{U_{i}}\circ \bar{\pi }_{i}\\= & {} \alpha _{U_{i}}\circ \bar{\pi }_{i} \end{aligned}$$

For the proof of Theorem 2, we note that the case where $R\upharpoonright U$ is empty becomes trivial. Otherwise fix any pair $(u_{1},u_{2})\in R\upharpoonright U$ and define the following inverses $\kappa _{i}$ to the inclusions $\iota _{i}:U_{i}\rightarrow A_{i}$:

$$\begin{aligned} \kappa _{i}(a)\,:=if\,(a\in U_{i})\,then\,a\,else\,u_{i}. \end{aligned}$$

Given $(a_{1},a_{2})\in R,$ the conditions $R[U_{1}]\subseteq U_{2}$ and $R^{-}[U_{2}]\subseteq U_{1}$ guarantee that $a_{1}\in U_{1}\iff a_{2}\in U_{2}$. By definition of $\kappa _{i}$ then, either $(\kappa _{1}a_{1},\kappa _{2}a_{2})=(a_{1},a_{2})$ or $(\kappa _{1}a_{1},\kappa _{2}a_{2})=(u_{1},u_{2})$.

4 Relationships Between Bisimilarity and Observational Equivalence

Bisimilarity and observational equivalence need not be distinguished in many classical systems, such as e.g. in Kripke structures. In particular, the famous Hennessy-Milner theorem [12] relates bisimilarity with logical equivalence. However, the generalization of this result to coalgebras, as given by Pattinson [17], demonstrates that logical equivalence should rather be related to observational equivalence. In hindsight, this appears obvious, as bisimilarity need not be transitive, whereas observational equivalence always is transitive, and clearly so is logical equivalence. Thus in the case of the Hennessy-Milner theorem, “luckily” both notions agreed. The reason for this is, that the type functor for Kripke-structures, is rather well behaved, in that it weakly preserves kernel pairs, even arbitrary pullbacks.

4.1 Weak Preservation of Kernel Pairs

A kernel pair is the pullback of two equal morphisms. A preimage is a pullback with a regular epimorphism. The role of weak preservation of pullbacks in general, of kernel pairs and of preimages has been studied by Gumm and Schröder [8]. In particular, we recall that:

Theorem 3

[8]. The following are equivalent :

(1) F weakly preserves kernel pairs (of epis).

(2) Every congruence is a bisimulation.

Thus weak preservation of kernel pairs is equivalent to all epis $\varphi$ being strictly regular, meaning that $[ker\,\varphi ]=ker\varphi$. We shall show below that this is equivalent to all epis just being regular, i.e. $[ker\,\varphi ]^{\star }=ker\,\varphi .$

A joint result of the second author and C. Henkel, to be found in the latter’s Master thesis [11], also turns out to be useful:

Theorem 4

[11]. The following are equivalent:

• 1. F weakly preserves kernel pairs

• 2. F weakly preserves pullbacks of epimorphisms.

In [8], furthermore, the implications $(1)\implies (2)\implies (3)$ have been shown for the following properties:

• 1. F weakly preserves kernel pairs

• 2. every epi is regular epi

• 3. every mono is regular mono.

In [20] it was further claimed that $(3)\Rightarrow (1)$, rendering all three properties equivalent. Unfortunately, the proof contained a gap, so until today, $(3)\Rightarrow (1)$ remains open. Nevertheless, we are able to close the loop at $(2)\Rightarrow (1)$ in the following Theorem 5, so (1) and (2) indeed turn out to be equivalent. The following innocuous lemma holds a key for the proof.

Lemma 7

Let $\varphi$ be the coequalizer of $\psi _{1},\psi _{2}:Q\rightarrow A$ and let $x\in A$. If there exists $y\ne x$ with $\varphi (x)=\varphi (y)$ then for some q in Q either $\psi _{1}(q)=x\ne \psi _{2}(q)$ or $\psi _{2}(q)=x\ne \psi _{1}(q).$

Proof

In the category Set, the coequalizer $\varphi$ of $\psi _{1}$ and $\psi _{2}$ is obtained by factoring A by the equivalence relation generated by the relation $R=\{(\psi _{1}(q),\psi _{2}(q))\,|\,q\in Q\}$. Thus $\text {ker}\,\varphi =Eq(R)=(\varDelta _{A}\cup R\cup R^{-})^{*}$. If $x\,\text {ker}\,y$ for some $y\ne x$, there must be therefore be at least some $y'\ne x$ with $xRy'$ or $xR^{-}y'$.

The following theorem was obtained in the master thesis of the first author:

Theorem 5

[24]. F weakly preserves kernel pairs iff every epi is regular epi.

Proof

“$\Rightarrow$” is from [8].

“$\Leftarrow$”: By Theorem 3 it suffices to show, that F preserves weak kernel pairs of epis. Let $\varphi :A\twoheadrightarrow C$ be a surjective map, $\tilde{a}$,$\tilde{b}$ $\in F(A)$ and $\tilde{c\,}$ $\in F(C)$ with $(F\varphi )\tilde{a}=\tilde{c}=(F\varphi )\tilde{b}$. We need to find $\tilde{p}\,$ $\in F(\text {ker}\varphi )$ with $(F\pi _{1})\tilde{p}=\tilde{a}$ and $(F\pi _{2})\tilde{p}=\tilde{b}$. In case $\varphi$ is injective, then the pullback of $\varphi$ is an intersection. We have assumed in this paper that functors preserve intersections. Otherwise there are $x,y\in A$ with $x\ne y$ and $\varphi (x)=\varphi (y)$. We define structure maps $\alpha _{A}:A\longrightarrow FA$ and $\alpha _{C}:C\longrightarrow FC$ as follows:

$$\begin{aligned} \,\,\,\alpha _{A}(z)&:={\left\{ \begin{array}{ll} \tilde{a} &{} if\ z=x\\ \tilde{b} &{} otherwise \end{array}\right. }\\&\text {and}\\ \,\,\,\alpha _{C}(z)&:=\tilde{c}. \end{aligned}$$

Clearly $\varphi$ is a surjective homomorphisms, since $(\alpha _{C}\circ \varphi )(z)=\alpha _{C}(\varphi (z))=\tilde{c}$ $=(F\varphi )(\alpha _{A}(z))$ $=((F\varphi )\circ \alpha _{A})(z)$ for every $z\in A$. By assumption $\varphi$ is regular epi, so it is the coequalizer of two homomorphisms $\psi _{1}$ and $\psi _{2}$: $Q\longrightarrow A$. By Lemma 7 there is some $q\in Q$ with $(\psi _{1}(q)=x$ and $\psi _{2}(q)\ne x)$ or $(\psi _{1}(q)\ne x$ and $\psi _{2}(q)=x)$. Since $\varphi$ is the coequalizer of $\psi _{1}$ and $\psi _{2}$, $(Q,\psi _{1},\psi _{2})$ becomes a competitor for the pullback $(\text {ker}\,\varphi ,\pi _{1},\pi _{2})$ in Set. Thus there is a map m with $\pi _{1}\circ m=\psi _{1}$ and $\pi _{2}\circ m=\psi _{2}$.

Since $\psi _{1}(q)=x$ and $\psi _{2}(q)\ne x$ it follows that $\alpha _{A}(\psi _{1}(q))=\tilde{a}$ and $\alpha _{A}(\psi _{2}(q))=\tilde{b.}$ Then $F\psi _{1}\circ \alpha _{Q}(q)=\tilde{a}$ and $F\psi _{2}\circ \alpha _{Q}(q)=\tilde{b}$ because $\psi _{1}$ and $\psi _{2}$ are homomorphisms. From property of functor this implies: $F\pi _{1}\circ Fm\circ \alpha _{Q}(q)=\tilde{a}$ and $F\pi _{2}\circ Fm\circ \alpha _{Q}(q)=\tilde{b}.$ Then $F\pi _{1}(Fm\circ \alpha _{Q}(q))=\tilde{a}$ and $F\pi _{2}(Fm\circ \alpha _{Q}(q))=\tilde{b}$. This shows the existence of some $\tilde{p}\,$ $\in F\text {ker}\,\varphi$ with $(F\pi _{1})\tilde{p}=\tilde{a}$ and $(F\pi _{2})\tilde{p}=\tilde{b}$.

Lemma 8

If an epimorphism $\varphi :\mathcal {U}\twoheadrightarrow \mathcal {B}$ can be factored as $\varphi =\psi \circ e$ with $e:{\mathcal {U}}\hookrightarrow \mathcal {A}$ regular mono and $\psi :\mathcal {A}\twoheadrightarrow \mathcal {B}$ a strictly regular epi, then $\varphi$ is strictly regular epi.

Proof

If $U=\emptyset$ then $\text {ker}\,\varphi =\emptyset$ is a bisimulation, so we may assume that $U\not =\emptyset$. Since $\varphi$ is epi, then $\varphi$ is surjective and the axiom of choice yields a right inverse map r for $\varphi$. With its help we obtain a map $l:A\longrightarrow U$ as

$$\begin{aligned} l(x):={\left\{ \begin{array}{ll} u &{} if\ e(u)=x\\ r(\psi (x)) &{} otherwise. \end{array}\right. } \end{aligned}$$

It is easy to check that $\varphi \circ l=\psi .$

$(\text {ker}\,\varphi ,e\circ \pi _{1},e\circ \pi _{2})$ is a competitor to the pullback $\text {ker}\,\psi$. This yields a map $m:\text {ker}\,\varphi \longrightarrow \text {ker}\,\psi$ with $\bar{\pi }_{i}\circ m=e\circ \pi _{i}$ for $i=1,2$. Similarly, $(\text {ker}\,\psi ,l\circ \bar{\pi }_{1},l\circ \bar{\pi }_{2})$ is a competitor to the pullback $\text {ker}\,\varphi$, providing another map $\bar{m}:\text {ker}\,\psi \longrightarrow \text {ker}\varphi$ with $l\circ \bar{\pi }_{i}=\pi _{i}\circ \bar{m}$. Now let us assume that $\text {ker}\,\psi$ is a bisimulation, then there exists a structure map $\rho :\text {ker}\,\psi \longrightarrow F\,\text {ker}\,\psi$ such that $\alpha _{\mathcal {A}}\circ \bar{\pi }_{i}=F\bar{\pi }_{i}\circ \rho$ for $i=1,2.$

We claim that $\rho ':=F\bar{m}\circ \rho \circ m$ is a structure map witnessing that $\text {ker}\,\varphi$ is a bisimulation.

$$\begin{aligned} F\pi _{i}\circ \rho '= & {} F\pi _{i}\circ F\bar{m}\circ \rho \circ m\\= & {} Fl\circ F\bar{\pi }_{i}\circ \rho \circ m\\= & {} Fl\circ \alpha _{\mathcal {A}}\circ \bar{\pi }_{i}\circ m\\= & {} Fl\circ \alpha _{\mathcal {A}}\circ e\circ \pi _{i}\\= & {} Fl\circ Fe\circ \alpha _{\mathcal {U}}\circ \pi _{i}\\= & {} \alpha _{\mathcal {U}}\circ \pi _{i} \end{aligned}$$

Lemma 9

Let $\varphi :\mathcal {A}\twoheadrightarrow \mathcal {B}$ be an epimorphism. $\varphi$ is strictly regular epi iff $[\varphi ,id_{B}]$ is strictly regular epi.

Proof

“$\Rightarrow$” : $\text {ker}\,[\varphi ,id_{B}]=\text {ker}\,\varphi \,\cup \text {graph}\,\varphi \cup (\text {graph}\,\varphi )^{-}\cup \varDelta _{A+B}$. Since $\text {ker}\,\varphi$ is bisimulation, $\text {ker}\,[\varphi ,id_{B}]$ is bisimulation, too.

“$\Leftarrow$” $[\varphi ,id_{B}]$ is regular epi by Lemma 1 and $e_{\mathcal {A}}$ is regular mono since it is injective. The rest follows from Lemma 8.

Proposition 1

Let $\varphi :\mathcal {A}\longrightarrow \mathcal {B}$ and $\psi :\mathcal {C}\longrightarrow \mathcal {D}$ be two homomorphisms. $\varphi$ and $\psi$ are regular epi iff $\varphi +\psi$ is regular epi.

Proof

“$\Rightarrow$” This holds in every cocomplete category [2].

“$\Leftarrow$” By Corollary 2 $[\text {ker}(\varphi +\psi )]_{\mathcal {A}+\mathcal {C}}=[\text {ker}\,\varphi ]_{\mathcal {A}}\cup [\text {ker}\,\psi ]_{\mathcal {C}}$. By Lemma 2 $\text {ker}\,\varphi \cup \text {ker}\,\psi =\text {ker}(\varphi +\psi )=[\text {ker}(\varphi +\psi )]_{\mathcal {A}+\mathcal {C}}^{*}=[\text {ker}\,\varphi ]_{\mathcal {A}}^{*}\cup [\text {ker}\,\psi ]_{\mathcal {C}}^{*}$. Then $\text {ker}\,\varphi =[\text {ker}\,\varphi ]_{\mathcal {A}}^{*}$ and $\text {ker}\,\psi =[\text {ker}\,\psi ]_{\mathcal {A}}^{*}$. From Lemma 2 it then follows that $\varphi$ and $\psi$ are regular epi.

We define an order over all homomorphisms with the same domain by $\varphi \le \psi \ :\Leftrightarrow \text {ker}\,\varphi \subseteq \text {ker}\,\psi$

Lemma 10

For any epimorphism $\varphi :A\twoheadrightarrow B$, the infimum of $id_{B}+[\varphi ,id_{B}]$ and $[id_{B},\varphi ]+id_{B}$ is $id_{B}+\varphi$ $+id{}_{B}.$

Proof

Mark the two isomorphic copies of B as $B_{1}$ and $B_{2}$ and abbreviate $\psi _{1}:=id_{B_{1}}+[\varphi ,id_{B_{2}}]$, $\psi _{2}:=[id_{B_{1}},\varphi ]+id_{B_{2}}$ and $\psi :=id_{B_{1}}+\varphi +id{}_{B_{2}}.$ We need to check that $\ker \psi =\ker \psi _{1}\cap \ker \psi _{2}$. Given $x\ne y$, then

$$\begin{aligned} (x,y)\in \ker \psi _{1}\cap \ker \psi _{2}\iff & {} \exists (a,a')\in \ker \varphi .\,x=e_{A}(a)\,\wedge y=e_{A}(a')\\\iff & {} (x,y)\in \ker \psi . \end{aligned}$$

Theorem 6

The following are equivalent:

• 1. F preserves weak kernel pairs,

• 2. $R^{d}$ is a bisimulation, whenever R is,

• 3. $[\theta ]$ is difunctional for each $2-$congruence $\theta$,

• 4. $[\theta ]$ is transitive for each congruence $\theta$,

• 5. $[\theta ]^{*}=\theta$ for every congruence $\theta$,

• 6. the regular congruences form a sublattice of $Cong(\mathcal {A})$.

Proof

(1)$\Rightarrow$(2) Let R be a bisimulation between two coalgebras $\mathcal {A}_{1}$ and $\mathcal {A}_{2}$. We factor the projections $\pi _{i}^{R}:R\rightarrow \mathcal {A}_{i}$ into $\iota _{i}\circ \bar{\pi }_{i}^{R}$ as an epi followed by a regular mono and produce the pushout $(p_{1},p_{2})$ of $(\bar{\pi }_{1}^{R},\bar{\pi }_{2}^{R})$. Then $p_{1}$ and $p_{2}$ are epi and.$R^{d}=\text {ker}(p_{1},p_{2}).$ It follows from Theorem 4 that $R^{d}$ is a bisimulation.

(2) $\Rightarrow$ (3) is evident

(3) $\Rightarrow$ (4) If $\theta$ is a congruence, $[\theta ]$ also must be reflexive and symmetric. Considered as a $2-$congruence between $\mathcal {A}$ and itself, the hypothesis yields that $[\theta ]$ is difunctional, too. Difunctionality with reflexivity and symmetry implies transitivity.

(4) $\Rightarrow$ (5) $\theta =\text {ker}\varphi$ for some epimorphism $\varphi :\mathcal {A}\twoheadrightarrow \mathcal {B}$. By Lemma 1, $\text {ker}[\varphi ,id_{\mathcal {B}}]$ is a regular congruence, so $\text {ker}[\varphi ,id_{\mathcal {B}}]=[\text {ker}[\varphi ,id_{\mathcal {B}}]]^{\star }$. By hypothesis, $[\text {ker}[\varphi ,id_{\mathcal {B}}]]$ is transitive, so in fact $\text {ker}[\varphi ,id_{\mathcal {B}}]=[\text {ker}[\varphi ,id_{\mathcal {B}}]]$, witnessing that $\text {ker}[\varphi ,id_{\mathcal {B}}]$ is a bisimulation. From Lemma 9, we can conclude now, that $\ker \varphi =\theta$ is a bisimulation, too. Consequently, $\theta =[\theta ]$ and a fortiori $\theta =\theta ^{\star }=[\theta ]^{\star }.$

$(5)\Rightarrow (6)$ is evident, because all congruences are regular.

$(6)\Rightarrow (1)$ Let $\varphi :A\twoheadrightarrow B$ be an epimorphism. Let $\psi _{1}:B+A+B\longrightarrow B+B$, $\psi _{2}:B+A+B\longrightarrow B+B$ and $\psi :B+A+B\longrightarrow B+B+B$ be defined as $\psi _{1}:=id_{B}+[\varphi ,id_{B}]$, $\psi _{2}:=[id_{B},\varphi ]+id_{B}$ and $\psi :=id_{B}+\varphi +id_{B}$. From Lemma 1 and Proposition 1 we obtain that $\psi _{1}$ and $\psi _{2}$ are regular epis. From the hypothesis it follows that the infimum of $\psi _{1}$ and $\psi _{2}$ is regular epi. By Lemma 10 then $\psi$ is regular epi. By Lemma 1 then $\varphi$ is again regular epi.

4.2 Transitivity of $\sim$

The next theorem clarifies which properties assure the transitivity of bisimilarity. The equivalence (1) $\Leftrightarrow$ (3) appears in [8] under the additional assumption that F should preserve preimages. Its proof will need a simple lemma allowing us to extend bisimulations in certain situations.

Theorem 7

The following are equivalent:

(1) $\sim _{\mathcal {A}}=\nabla _{\mathcal {A}}$ for each $F-$coalgebra $\mathcal {A}$.

(2) $\sim _{\mathcal {A}}^{*}=\nabla _{\mathcal {A}}$ for each $F-$coalgebra $\mathcal {A}$.

(3) $\sim _{\mathcal {A}}$ is transitive for each $F-$coalgebra $\mathcal {A}$:

Proof

$(1)\Rightarrow (2)$ and $(1)\Rightarrow (3)$ are evident, since $\nabla _{\mathcal {A}}$ is transitive.

($2)\Rightarrow (1)$: Given $\mathcal {A}=(A,\alpha )$, we have to show that $\nabla _{\mathcal {A}}$ is a bisimulation. Hence for arbitrary $(x_{0},y_{0})\in \nabla _{\mathcal {A}}$ we need to find some $p\in F\nabla _{\mathcal {A}}$ with $F\pi _{1}(p)=\alpha (x_{0})$ and $F\pi _{2}(p)=\alpha (y_{0})$ where $\pi _{1},\pi _{2}:\nabla _{\mathcal {A}}\rightarrow A$ are the projection maps.

If $x_{0}=y_{0}$ then $(x_{0},y_{0})\in \varDelta _{A}$ which is already a bisimulation contained in $\nabla _{\mathcal {A}}$. But for each bisimulation S contained in $\nabla _{A}$ with $(x_{0},y_{0})\in S$ there is already some $q\in F(S)$ with $F\pi _{A}^{S}(q)=\alpha (x_{0})$ and $F\pi _{A}^{S}(q)=\alpha (x_{0})$. The inclusion map $\iota _{S}^{\nabla }:S\hookrightarrow \nabla _{A}$ yields an element $p:=F\iota _{S}^{\nabla }(q)\in F(\nabla _{A})$ for which $F\pi _{1}(p)=F\pi _{1}(F\iota _{S}^{\nabla }(q)=F(\pi _{1}\circ \iota _{S}^{\nabla })(q)=F(\pi _{1}^{S})(q)=\alpha (x_{0})$, and likewise $F\pi _{2}(p)=\alpha (y_{0}).$

If $x_{0}\ne y_{0}$, we consider $\bar{\mathcal {A}}:=\mathcal {A}_{x_{0}}^{U}$ (see Definition 9), where we choose $U:=\{x\mid x_{0}\nabla _{\mathcal {A}}x\ne y_{0}\}$. Invoking Lemma 6 with $\pi _{\nabla _{\mathcal {A}}}:\mathcal {A}\rightarrow \mathcal {A}/\nabla _{\mathcal {A}}$ and recalling that $\mathcal {A}/\nabla _{\mathcal {A}}$ is simple, we obtain $\nabla _{\bar{\mathcal {A}}}=\nabla _{\mathcal {A}}=:\nabla$. By assumption (2), there is a bisimulation S on $\bar{\mathcal {A}}$ with $S^{\star }=\nabla ,$ so in particular $x_{0}S^{\star }y_{0}$. As $x_{0}\ne y_{0}$, there is some $z\ne y_{0}$ with $x_{0}\,S^{\star }z\,S\,y_{0}$ and a fortiori $x_{0}\nabla zSy_{0}$. Since S is a bisimulation on $\bar{\mathcal {A}}$, there is some $q\in F(S)$ with $F\pi _{1}(q)=\bar{\alpha }(z)=\alpha (x_{0})$ and $F\pi _{2}(q)=\bar{\alpha }(y_{0})=\alpha (y_{0})$.

(3) $\Rightarrow$ (1):

By Lemma 1 $[\pi _{\nabla },id_{A/\nabla }]$ is regular epi. From Theorem 2 we obtain $\sim _{A+A_{\nabla }}^{*}=\nabla _{A+A/\nabla }$. Then

$$\begin{aligned}{}[\text {ker}\,[\pi _{\nabla },id_{A_{\nabla }}]]&=[\nabla _{A+A/\nabla }]&\text {lemma }3\\&=\sim _{A+A_{\nabla }}\\&=\sim _{A+A_{\nabla }}^{*}&\text {hypothesis}\\&=\text {ker}\,[\pi _{\nabla },id_{A/\nabla }]. \end{aligned}$$

Therefore, $\text {ker}\,[\pi _{\nabla },id_{A/\nabla }]$ is a bisimulation, and by Lemma 9, $\nabla$ is a bisimulation.

For image finite Kripke structures $\mathcal {A}$, i.e. coalgebras for $D\times \mathbb {P}_{fin}$ where D is a fixed output set and $\mathbb {P}_{fin}$ the finite-powerset functor, it is well known that $\sim _{\mathcal {A}}=\nabla _{\mathcal {A}}.$ However, considered as a coalgebra of $D\times \mathbb {P}_{\le k}$ where $\mathbb {P}_{\le k}X:=\{U\subseteq X\,|\,|U|\le k\}$ the same Kripke structure may fail to satisfy $\sim _{\mathcal {A}}=\nabla _{\mathcal {A}}$. The fact that for $k\ge 3$ the functor $\mathbb {P}_{\le k}$, defined as a subfunctor of $\mathbb {P}$, does not preserve weak kernel pairs was noticed in [8].

4.3 Difunctionality of $\sim$

In an attempt to generalize the results of the previous subsection to relations between two coalgebras, we consider the following conditions:

• 1. For all $F-$coalgebras $\mathcal {A},\mathcal {B}$: $\sim _{\mathcal {A},\mathcal {B}}=\nabla _{\mathcal {A},\mathcal {B}}$

• 2. For all $F-$coalgebras $\mathcal {A},\mathcal {B}$: $\sim _{\mathcal {A},\mathcal {B}}^{d}=\nabla _{\mathcal {A},\mathcal {B}}$

• 3. For all $F-$coalgebras $\mathcal {A},\mathcal {B}$: $\sim _{\mathcal {A},\mathcal {B}}$ is difunctional.

We will show in the next section that the direction $(2)\Rightarrow (1)$ holds more generally, yet the implication (3) $\Rightarrow$ (1) fails in general. We provide a counterexample (Example 2) in the next section. We will use the following characterization of preimages preservation.

Theorem 8

[6]. The following are equivalent:

(1) F preserves preimages

(2) If $\mathcal {U},\,\mathcal {V}$ are subcoalgebras of $\mathcal {A},\,\mathcal {B}$ then bisimulations between $\mathcal {U}$ and $\mathcal {V}$ are just the restrictions to $U\times V$ of bisimulations between $\mathcal {A}$ and $\mathcal {B}$.

Under the assumption that F should preserves preimages we will see that difunctionality and transitivity of bisimulations are equivalent.

Theorem 9

If F preserves preimages, then the following are equivalent:

(1) For all $F-$coalgebras $\mathcal {A},\mathcal {B}$: $\sim _{\mathcal {A},\mathcal {B}}=\nabla _{\mathcal {A},\mathcal {B}}$

(2) For all $F-$coalgebras $\mathcal {A},\mathcal {B}$: $\sim _{\mathcal {A},\mathcal {B}}$ is difunctional.

(3) For all $F-$coalgebras $\mathcal {A}$: $\sim _{\mathcal {A}}=\nabla _{\mathcal {A}}$.

Proof

(1)$\Rightarrow$ (2) is evident because $\nabla _{\mathcal {A},\mathcal {B}}$ is difunctional.

(2) $\Rightarrow$ (3) From the hypothesis it follows that $\sim _{\mathcal {A}}$ is transitive for all $F-$coalgebras $\mathcal {A}$, because $\sim _{\mathcal {A}}$ is reflexive and symmetric. By Theorem 7 we obtain that for all $F-$coalgebras $\mathcal {A}$: $\sim _{\mathcal {A}}=\nabla _{\mathcal {A}}$.

(3) $\Rightarrow$ (1) Let $\mathcal {A}=(A,\alpha )$ and $\mathcal {B}=(B,\beta )$ two coalgebra. We have to show $\sim _{\mathcal {A},\mathcal {B}}=\nabla _{\mathcal {A},\mathcal {B}}$.

$$\begin{aligned} (a,b)\in \nabla _{\mathcal {A},\mathcal {B}}&\iff \,(e_{A}(a),e_{B}(b))\in \nabla _{\mathcal {A}+\mathcal {B}}&\text {by lemma }4\\&\iff \,(e_{A}(a),e_{B}(b))\in \sim _{\mathcal {A}+\mathcal {B}}&\text {by hypothesis}\\&\iff \,(a,b)\sim _{\mathcal {A},\mathcal {B}}&\text {by theorem }8. \end{aligned}$$

4.4 Relation Liftings

An alternative definition of bisimulation was given by C. Hermida and B. Jacobs in [13]. The idea is to define a bisimulation R as a relation $R\subseteq A\times B$ satisfying:

$$ x\,R\,y\implies \alpha (x)\,\bar{F}(R)\,\alpha (y) $$

where $\bar{F}$ is the “lifting” of the relation $R\subseteq A\times B$ to a relation $\bar{F}(R)\subseteq F(A)\times F(B)$, known as Barr-extension:

$$ \bar{F}(R):=\{(F\pi _{A}^{R}(u),F\pi _{B}^{R}(u))\mid u\in F(R)\}. $$

Choosing the Barr-extension may be one particular method for extending a relation between A and B to a relation between F(A) and F(B), but there might likely be others, so we define:

Definition 11

A relation lifting L is a transformation sending every relation $R\subseteq A\times A$ into a relation $L(R)\subseteq FA\times FB$. It is called monotonic, if $R\subseteq S$ implies $L(R)\subseteq L(S)$. For a given relation lifting L and coalgebras $\mathcal {A}=(A,\alpha _{\mathcal {A}})$ and $\mathcal {B}=(B,\alpha _{\mathcal {B}})$, an $L-$simulation is a relation $R\subseteq A\times B$ such

$$ x\,R\,y\implies \alpha (x)\,L(R)\,\alpha (y). $$

Diagrammatically, R is an L-simulation if and only if the map sending (x, y) to $(\alpha _{\mathcal {A}}(x),\alpha _{\mathcal {B}}(y))$ factors through L(R), which is the same as saying that there exists a map m such that the following diagram commutes:

Thus a Hermida-Jacobs-bisimulation is the same as an $L-$simulation where $L=\bar{F}$. Observe, that categorically, $\bar{F}(R)$ arises by applying the functor F to the source $\pi _{A}^{R}:R\rightarrow A$ and $\pi _{B}^{R}:R\rightarrow B$, then factoring the resulting source $F\pi _{A}^{R}:F(R)\rightarrow F(A)$ and $F\pi _{B}^{R}:F(R)\rightarrow F(B)$, into an epi q followed by a mono-source:

This diagram can be readily used to demonstrate the well known fact that our earlier definition of bisimulation agrees with that of Hermida and Jacobs in the presence of the axiom of choice. When $L=\bar{F}$, we can paste it to the bottom line of the previous diagram in order to see that any bisimulation $\rho :R\rightarrow F(R)$ yields an $\bar{F}-$simulation and conversely, any choice of right inverse e for q yields a bisimulation $\rho :=e\circ m$.

Thijs in [22] defined relators as relation liftings with additional properties and generalized the notion of coalgebraic simulation. In [15] Marti and Venema introduced further properties, in an attempt to achieve that $L-$similarity should capture observational equivalence. The union of all $L-$simulations between given coalgebra $\mathcal {A}$ and $\mathcal {B}$ is denoted by $\thickapprox _{\mathcal {A},\mathcal {B}}^{L}$. If L is monotonic then $\thickapprox _{\mathcal {A},\mathcal {B}}^{L}$ is again an $L-$simulation. For $L=\bar{F}$, of course, $\thickapprox _{\mathcal {A},\mathcal {B}}^{L}$ agrees with $\sim _{\mathcal {A},\mathcal {B}}$.

In [15] it was also shown that there is no relation lifting L for the neighborhood functor which captures observational equivalence in the sense that $\approx _{\mathcal {A},\mathcal {B}}^{L}=\nabla _{\mathcal {A},\mathcal {B}}$ for all coalgebras $\mathcal {A},\mathcal {B}$. In particular, for this functor there are coalgebras $\mathcal {A}$ and $\mathcal {B}$ such that $\sim _{\mathcal {A},\mathcal {B}}\ne \nabla _{\mathcal {A},\mathcal {B}}$.

Example 2

Consider the neighborhood functor $2^{2^{-}}$. From Theorem 6 $\sim _{\mathcal {A},\mathcal {B}}$ is difunctional for all coalgebras $\mathcal {A},\mathcal {B}$, since $2^{2^{-}}$ weakly preserves kernel pairs [10]. But $\sim _{\mathcal {A},\mathcal {B}}=\nabla _{\mathcal {A},\mathcal {B}}$ does not hold.

In [9] we have shown, that bisimulations can be enlarged as long as the structure maps are not affected in the following sense:

Proposition 2

[9]. Let $\mathcal {A}_{1}$ and $\mathcal {A}_{2}$ be coalgebras with corresponding structure maps $\alpha _{1}$ and $\alpha _{2}$. Let $R\subseteq \mathcal {A}_{1}\times \mathcal {A}_{2}$ be a bisimulation and $R'$ an enlargement i.e. $R\subseteq R'\subseteq ker\,\alpha _{1}\circ R\circ ker\,\alpha _{2}$. Then $R'$ is also a bisimulation.

A relation lifting L is called extensible, if for all coalgebras $\mathcal {A}_{1}$ and $\mathcal {A}_{2}$ the statement of the above proposition holds with “bisimulation” replaced by “$L-$simulation”. It turns out, that this property precisely captures monotonicity, i.e.:

Proposition 3

A relation lifting L is monotonic iff it is extensible.

Proof

The proof of the if-direction closely follows, but is not identical to, the proof of Proposition 2 from [9]: R is a $L-$simulation, so there exists a map $\rho :R\rightarrow L(R)$ with $\alpha _{i}\circ \pi _{i}^{R}=\pi _{i}^{LR}\circ \rho$. Let $\iota :R\rightarrow R'$ be the inclusion map, then clearly $\pi _{i}^{R}=\pi _{i}^{R'}\circ \iota$. By assumption, we find for every $(x',y')\in R'$ a pair $(x,y)\in R$ such that $\alpha _{1}(x)=\alpha _{1}(x')$ and $\alpha _{2}(y)=\alpha _{2}(y').$ The axiom of choice provides for a map $\mu :R'\rightarrow R$ satisfying

$$ \alpha _{i}\circ \pi _{i}^{R'}\circ \iota \circ \mu =\alpha _{i}\circ \pi _{i}^{R'}. $$

We now define $\rho ':R'\rightarrow L(R')$ by $\rho ':=\subseteq \circ \rho \circ \mu$.

For the only-if direction, let $R\subseteq R'\subseteq A_{1}\times A_{2}$ and $(\tilde{x},\tilde{y})\in LR$. We have to show $(\tilde{x},\tilde{y})\in LR'$. Since $(\tilde{x},\tilde{y})\in LR$ then R is a $L-$simulation between $(A_{1},c_{\tilde{x}})$ and $(A_{2},c_{\tilde{y}})$. By the hypothesis $R'$ is also a $L-$simulation. Then $(\tilde{x},\tilde{y})\in LR'$.

With the help of this proposition, we can now somehow simplify the task of proving that $\approx _{\mathcal {A},\mathcal {B}}^{L}$ captures observational equivalence, provided that L is monotonic:

Theorem 10

For a monotonic relation lifting L, the following are equivalent:

• 1. For all coalgebras $\mathcal {A},\mathcal {B}$: $\approx _{\mathcal {A},\mathcal {B}}=\nabla _{\mathcal {A},\mathcal {B}}$

• 2. For all coalgebras $\mathcal {A},\mathcal {B}$: $\approx _{\mathcal {A},\mathcal {B}}^{d}=\nabla _{\mathcal {A},\mathcal {B}}$

Proof

(1) $\Rightarrow$ (2) is evident as $\nabla _{\mathcal {A},\mathcal {B}}$ is difunctional.

(2) $\Rightarrow$ (1): For any $\mathcal {A}=(A,\alpha )$ and $\mathcal {B}=(B,\beta )$, we have to show that $\nabla _{\mathcal {A},\mathcal {B}}$ is an $L-$simulation. Given $(x_{0},y_{0})\in \nabla _{\mathcal {A},\mathcal {B}}$, let $U:=[x_{0}]\nabla _{\mathcal {A}}$ and $V:=[y_{0}]\nabla _{\mathcal {B}}$, let $\varphi :=\pi _{\nabla _{\mathcal {A}+\mathcal {B}}}\circ e_{\mathcal {A}}$ and $\psi :=\pi _{\nabla _{\mathcal {A}+\mathcal {B}}}\circ e_{\mathcal {B}}.$ Since $\mathcal {A}+\mathcal {B}/\nabla _{\mathcal {A}+\mathcal {B}}$ is simple, it follows from Lemma 5 that $\text {ker}\,\varphi =\nabla _{\mathcal {A}}$ and $\text {ker}\,\psi =\nabla _{\mathcal {B}}$. We define now two coalgebras $\bar{\mathcal {A}}:=\mathcal {A}_{x_{0}}^{U}$ and $\bar{\mathcal {B}}:=\mathcal {B}_{y_{0}}^{V}$ as in Definition 9. Since $U\subseteq [x_{0}]\text {ker}\,\varphi$ and $V\subseteq [x_{0}]\text {ker}\,\psi$, we can use Lemma 6 to see that both $\varphi :\bar{\mathcal {A}}\longrightarrow \mathcal {A}+\mathcal {B}/\nabla _{\mathcal {A}+\mathcal {B}}$ and $\psi :\bar{\mathcal {B}}\longrightarrow \mathcal {A}+\mathcal {B}/\nabla _{\mathcal {A}+\mathcal {B}}$ are homomorphisms to a simple coalgebra, so by Lemma 5, $\nabla _{\bar{\mathcal {A}},\bar{\mathcal {B}}}=\text {ker}(\varphi ,\psi )=\nabla _{\mathcal {A},\mathcal {B}}$. By hypothesis $(x_{0},y_{0})\in \approx _{\bar{\mathcal {A}},\bar{\mathcal {B}}}^{d}$, so there is $x_{1}\in A$ with $x_{1}\approx _{\bar{\mathcal {A}},\bar{\mathcal {B}}}y_{0}$. From $\approx _{\bar{\mathcal {A}},\bar{\mathcal {B}}}^{d}=\nabla _{\mathcal {A},\mathcal {B}}$ it follows that $\approx _{\bar{\mathcal {A}},\bar{\mathcal {B}}}\subseteq \nabla _{\mathcal {A},\mathcal {B}}$, so $(x_{1},y_{0})\in \nabla _{\mathcal {A},\mathcal {B}}$. Hence $\varphi (x_{1})=\psi (y_{0})=\varphi (x_{0})$ and consequently $(x_{0},x_{1})\in \text {ker}\,\varphi =\nabla _{\mathcal {A}}$. By construction of $\bar{\mathcal {A}}$ then $\bar{\alpha }(x_{1})=\alpha (x_{0})=\bar{\alpha }(x_{0})$. With the help of Proposition 3 we obtain $x_{0}\approx _{\bar{\mathcal {A}},\bar{\mathcal {B}}}y_{0}$. Hence $(\bar{\alpha }(x_{0}),\bar{\beta }(y_{0}))\in L\approx _{\bar{\mathcal {A}},\bar{\mathcal {B}}}$ and finally $(\alpha (x_{0}),\beta (y_{0}))\in L\nabla _{\mathcal {A},\mathcal {B}}$ since $\approx _{\bar{\mathcal {A}},\bar{\mathcal {B}}}\subseteq \nabla _{\mathcal {A},\mathcal {B}}$ and L is monotonic.

The Barr extension $\bar{F}$ is an example of a monotonic relation lifting, so we obtain:

Corollary 3

The following are equivalent:

• 1. For all coalgebras $\mathcal {A},\mathcal {B}$: $\sim _{\mathcal {A},\mathcal {B}}=\nabla _{\mathcal {A},\mathcal {B}}.$

• 2. For all coalgebras $\mathcal {A},\mathcal {B}$: $\sim _{\mathcal {A},\mathcal {B}}^{d}=\nabla _{\mathcal {A},\mathcal {B}}.$

5 Conclusion and Further Work

In this paper we exhibited conditions under which bisimulations restrict to subcoalgebras without requiring the type functor to preserve preimages. Further, we have shown that if the transitive, resp. difunctional hull of bisimilarity covers observational equivalence then bisimilarity and observational equivalence agree. If bisimilarity is transitive for all F-coalgebras, then it agrees with observational equivalence.

A negative result is that difunctionality is not enough to cover observational equivalence between two coalgebras. Assuming preimage preservation for the type functor F, transitivity and difunctionality of bisimilarity are equivalent.

We also show that F weakly preserves kernel pairs if and only if every epi is regular epi. While it is known that this implies that every mono is regular mono, the converse remains an open question.

A further open question is: If every extensional coalgebra is simple, does this mean that $\sim _{\mathcal {A}}=\nabla _{\mathcal {A}}$ for all coalgebras $\mathcal {A}$? In order to put this question into a more general framework, we plan to investigate $L-$ extensionality for arbitrary relation liftings L.