Abstract
In open systems exhibiting adaptation, behaviors can arise as side effects of intensive components interaction. Finding ways to understand and design these systems, is a difficult but important endeavor. To tackle these issues, we present AbC, a calculus for attribute-based communication. An AbC system consists of a set of parallel agents each of which is equipped with a set of attributes. Communication takes place in an implicit multicast fashion, and interactions among agents are dynamically established by taking into account “connections” as determined by predicates over the attributes of agents. First, the syntax and the semantics of the calculus are presented, then expressiveness and effectiveness of AbC are demonstrated both in terms of modeling scenarios featuring collaboration, reconfiguration, and adaptation and of the possibility of encoding channel-based interactions and other interaction patterns. Behavioral equivalences for AbC are introduced for establishing formal relationships between different descriptions of the same system.
This research has been partially supported by the European projects IP 257414 ASCENS and STReP 600708 QUANTICOL, and by the Italian project PRIN 2010LHT4KM CINA.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
In a world of Internet of Things (IoT), of Systems of Systems (SoS), and of Collective Adaptive Systems (CAS), most of the concurrent programming models still rely on communication primitives based on point-to-point, multicast with explicit addressing (i.e. IP multicast [13]), or on broadcast communication. In our view, it is important to consider alternative basic interaction primitives and in this paper we study the impact of a new paradigm that permits selecting groups of partners by considering the (predicates over the) attributes they expose.
The findings we report in this paper have been triggered by our interest in CAS, see e.g. [10], and the recent attempts to define appropriate linguistic primitives to deal with such systems, see e.g. TOTA [17], SCEL [7] and the calculi presented in [3, 28]. CAS consists of large numbers of interacting components which exhibit complex behaviors depending on their attributes and objectives. Decision-making is complex and interaction between components may lead to unexpected behaviors. Components work in an open environment and may have different (potentially conflicting) objectives; so they need to dynamically adapt to their contextual conditions. New engineering techniques to address the challenges of developing, integrating, and deploying such systems are needed [26].
To move towards this goal, in our view, it is important to develop a theoretical foundation for this class of systems that would help in understanding their distinctive features. In this paper, we present AbC, a calculus comprising a minimal set of primitives that permit attribute-based communication. AbC systems are represented as sets of parallel components, each is equipped with a set of attributes whose values can be modified by internal actions. Communication actions (both send and receive) are decorated with predicates over attributes that partners have to satisfy to make the interaction possible. Thus, communication takes place in an implicit multicast fashion, and communication partners are selected by relying on predicates over the attributes in their interfaces. The semantics of output actions is non-blocking while input actions are blocking.
Many communication models addressing distributed systems have been introduced so far. Some of the well-known approaches include: channel-based models (e.g., CCS [18], CSP [12], \(\pi \)-calculus [20], etc.), group-based models [1, 5, 13], and publish/subscribe models [4, 9]. The advantage of AbC over channel-based models is that interacting partners are anonymous to each other. Rather than agreeing on channels or names, they interact by relying on the satisfaction of predicates over their attributes. This makes AbC more suitable for modeling scalable distributed systems as anonymity is a key factor for scalability. Furthermore, the spaces (i.e., groups) in group-based models like Actorspace [1] are regarded as containers of actors and should be created and deleted with explicit constructs, while in AbC, there is no need for such constructs. The notion of group in AbC is quite abstract and can be specified by means of satisfying the sender’s predicate at the time of interaction. On the other hand, the publish/subscribe model is a special case of AbC where publishers attach attributes to messages and send them with empty predicates (i.e., satisfied by all). Subscribers check the compatibility of the attached attributes with their subscriptions.
The concept of attribute-based communication can be exploited to provide a general unifying framework to encompass different communication models. Extended discussion for this paper can be found in the technical report in [2].
Contributions. (i) In Sects. 2 and 3, we present the AbC calculus, a refined and extended version of the one in [3]. The latter is a very basic calculus with a number of limitations, see Sect. 6 in [2]; (ii) we study the expressive power of AbC both in terms of the ability of modeling scenarios featuring collaboration, reconfiguration, and adaptation and of the possibility of modeling different interaction patterns, see Sect. 4; (iii) we define behavioral equivalences for AbC by first introducing a context based barbed congruence relation and then the corresponding extensional labelled bisimilarity, see Sect. 5; (iv) we show how to encode channel-based communication and prove the correctness of the encoding up to the introduced equivalence, see Sect. 6.
2 The AbC Calculus
The syntax of the AbC calculus is reported in Table 1. The top-level entities of the calculus are components (C), a component consists of either a process P associated with an attribute environment \(\varGamma \), denoted \(\varGamma _{}\!:\!{P}\), a parallel composition \(C_1\Vert C_2\) of two components, a replication !C which can always create a new copy of C. The attribute environment  is a partial map from attribute identifiers \(a \in \mathcal {A}\) to values \(v \in \mathcal {V}\) where \(\mathcal {A}\cap \mathcal {V}=\emptyset \). A value could be a number, a name (string), a tuple, etc. The scope of a name say n, can be restricted by using the restriction operator \(\nu n\). For instance, the name n in \(C_1\ \Vert \ \nu nC_2\) is only visible within component \(C_2\). Attribute values can be restricted while attribute identifiersFootnote 1 cannot, because they represent domain concepts. Each component in a system is aware of the set of attribute identifiers that represents the domain concepts.
is a partial map from attribute identifiers \(a \in \mathcal {A}\) to values \(v \in \mathcal {V}\) where \(\mathcal {A}\cap \mathcal {V}=\emptyset \). A value could be a number, a name (string), a tuple, etc. The scope of a name say n, can be restricted by using the restriction operator \(\nu n\). For instance, the name n in \(C_1\ \Vert \ \nu nC_2\) is only visible within component \(C_2\). Attribute values can be restricted while attribute identifiersFootnote 1 cannot, because they represent domain concepts. Each component in a system is aware of the set of attribute identifiers that represents the domain concepts.
A process is either the inactive process \(\mathsf{0}\), an action-prefixed process \(\bullet .P\) (where “\(\bullet \)” is replaced with an action), an attribute update process \([{\tilde{a}}:={\tilde{E}}]P\), an awareness process \(\langle {\varPi }\rangle P\), a choice between two processes \(P_1 + P_2\), a parallel composition between two processes \(P_1|P_2\), or a recursive call K. We assume that each process has a unique process definition \(K \triangleq P\). The attribute update construct in \([{\tilde{a}}:={\tilde{E}}]P\) sets the value of each attribute in the sequence \(\tilde{a}\) to the evaluation of the corresponding expression in the sequence \(\tilde{E}\).
The awareness construct in \(\langle {\varPi }\rangle P\) is used to test awareness data about a component status or its environment by inspecting the local attribute environment where the process resides. This construct blocks the execution of process P until the predicate \(\varPi \) becomes true. The parallel operator “|” models the interleaving between processes. In what follows, we shall use the notation \(\llbracket \varPi \rrbracket _{\varGamma }\) (resp. \(\llbracket E\rrbracket _{\varGamma }\)) to indicate the evaluation of a predicate \(\varPi \) (resp. an expression E) under the attribute environment \(\varGamma \). The evaluation of a predicate consists of replacing variable references with their values and returns the result.
There are two kinds of actions: the attribute-based input \(\varPi _{}({\tilde{x}})\) which binds to sequence \(\tilde{x}\) the corresponding received values from components whose communicated attributes or values satisfy the predicate \(\varPi \). The attribute-based output \(({\tilde{E}})@\varPi _{}\) which evaluates the sequence of expressions \(\tilde{E}\) under the attribute environment \(\varGamma \) and then sends the result to the components whose attributes satisfy the predicate \(\varPi \).
A predicate \(\varPi \) is either a binary operator \(\bowtie \) between two values or a propositional combination of predicates. Predicate \(\mathsf{tt}\) is satisfied by all components and is used when modeling broadcast while \(\mathsf{ff}\) is not satisfied by any component and is used when modeling silent moves. The satisfaction relation \(\models \) of predicates is presented in Table 2. In the rest of this paper, we shall use the relation  to denote a semantic equivalence for predicates as defined below.
to denote a semantic equivalence for predicates as defined below.
Definition 1
(Predicate Equivalence). Two predicates are semantically equivalent, written  , iff for every environment \(\varGamma \), it holds that:
, iff for every environment \(\varGamma \), it holds that:
\(\varGamma \models \varPi _1\) iff \(\varGamma \models \varPi _2\).
Clearly, the predicate equivalence, defined above, is decidable because we limit the expressive power of predicates by considering only standard boolean expressions and simple constraints on attribute values as shown in Table 2.
An expression E is either a constant value \(v \in \mathcal {V}\), a variable x, an attribute identifier a, or a reference to a local attribute value  . The properties of self-awareness and context-awareness that are typical for CAS are guaranteed in AbC by referring to the values of local attributes via a special name
. The properties of self-awareness and context-awareness that are typical for CAS are guaranteed in AbC by referring to the values of local attributes via a special name  (i.e.,
(i.e.,  ). These values represent either the current status of a component (i.e., self-awareness) or the external environment (i.e.,context-awareness). Expressions within predicates contain also variable names, so predicates can check whether the sent values satisfy specific conditions. This permits a sort of pattern-matching. For instance, component \(\varGamma :(x>2)(x, y)\) receives a sequence of values “x, y” from another component only if the value x is greater than 2.
). These values represent either the current status of a component (i.e., self-awareness) or the external environment (i.e.,context-awareness). Expressions within predicates contain also variable names, so predicates can check whether the sent values satisfy specific conditions. This permits a sort of pattern-matching. For instance, component \(\varGamma :(x>2)(x, y)\) receives a sequence of values “x, y” from another component only if the value x is greater than 2.
We assume that processes are closed, and the constructs \(\nu x\) and \(\varPi _{}({\tilde{x}})\) act as binders for names. We write bn(P) to denote the set of bound names of P. The free names of P are those that do not occur in the scope of any binder and are denoted by fn(P). The set of names of P is denoted by n(P). The notions of bound and free names are applied in the same way to components, but free names also include attribute values that do not occur in the scope of any binder.
3 AbC Operational Semantics
The operational semantics of \(AbC \) is defined in two steps: first we define a component level semantics and then we define a system level semantics.
3.1 Operational Semantics of Component
We use the transition relation  to define the local behavior of a component where Comp denotes a component and CLAB is the set of transition labels \(\alpha \) generated by the following grammar:
to define the local behavior of a component where Comp denotes a component and CLAB is the set of transition labels \(\alpha \) generated by the following grammar:
The \(\lambda \)-labels are used to denote AbC output and input actions respectively. The output and input labels contain the sender’s predicate \(\varPi \), and the transmitted values \(\tilde{v}\). An output is called “bound” if its label contains a bound name (i.e., if \(\tilde{x}\ne \emptyset \)). The \(\alpha \)-labels include an additional label \(\widetilde{\varPi (\tilde{v}){}}\) to denote the case where a process is not able to receive a message. This label is crucial to keep dynamic constructs (i.e., \(+\)) from dissolving after performing input refusal as it will be shown later in this section. Free names in \(\alpha \) are specified as follows:
-
\(fn(\nu \tilde{x}\overline{\varPi }(\tilde{v}))=fn(\varPi (\tilde{v}))\backslash \tilde{x}\qquad \) and \(fn({\varPi (\tilde{v})})=fn(\varPi ) \cup \tilde{v}\ \)
-
\(fn(\widetilde{\varPi (\tilde{v}){}})=fn(\varPi )\cup \tilde{v}\).
The \(fn(\varPi ) \) denotes the set of names occurring in the predicate \(\varPi \) except for attribute identifiers. Notice that  is only a reference to the value of the attribute identifier a. Only the output label has bound names (i.e., \(bn(\nu \tilde{x}\overline{\varPi }\tilde{v})=~\tilde{x}\)).
is only a reference to the value of the attribute identifier a. Only the output label has bound names (i.e., \(bn(\nu \tilde{x}\overline{\varPi }\tilde{v})=~\tilde{x}\)).
Component Semantics. The set of rules in Table 3 describes the behavior of a single AbC component. We omitted the symmetric rules for (Sum) and (Int).
Rule (Brd) evaluates the sequence of expressions \(\tilde{E}\) to \(\tilde{v}\) and the predicate \(\varPi _1\) to \(\varPi \) by replacing any occurring reference (i.e.,  ) to its value under \(\varGamma \), sends this information in the message, and the process evolves to P.
) to its value under \(\varGamma \), sends this information in the message, and the process evolves to P.
Rule (Rcv) replaces the free occurrences of the input sequence variables \(\tilde{x}\) in the receiving predicate \(\varPi \) with the corresponding message values \(\tilde{v}\) and evaluates \(\varPi \) under \(\varGamma \). If the evaluation semantically equals to \(\mathsf{tt}\) and \(\varGamma \) satisfies the sender predicate \(\varPi '\), the input action is performed and the substitution \([\tilde{v}/\tilde{x}]\) is applied to the continuation process P. Rule (Upd) evaluates the sequence \(\tilde{E}\) under \(\varGamma \), apply attribute updates i.e., \(\varGamma [\tilde{a}\mapsto \tilde{v}]\) where \( \forall a\in \tilde{a}\) and \( \forall v\in \tilde{v}\), \(\varGamma [a \mapsto v](a')=\varGamma (a')\) if \(a \ne a'\) and v otherwise, and then performs an action with a \(\lambda \) label if process P under the updated environment can do so.
Rule (Aware) evaluates the predicate \(\varPi \) under \(\varGamma \). If the evaluation semantically equals to \(\mathsf{tt}\), process \( \langle {\varPi }\rangle P\) proceeds by performing an action with a \(\lambda \)-label and continues as \(P'\) if process P can perform the same action.
Rule (Sum) and its symmetric version represent the non-deterministic choice between the subprocesses \(P_1\) and \(P_2\). Rule (Rec) is standard for process definition. Rule (Int) models the standard interleaving between two processes.
Discarding Input. The set of rules in Table 4 describes the meaning of the discarding label \(\widetilde{\varPi (\tilde{v}){}} \). Rule (FBrd) states that any sending process discards messages from other processes and stays unchanged. Rule (FRcv) states that if one of the receiving requirements is not satisfied then the process will discard the message and stay unchanged.
Rule (FUpd) state that process \([{\tilde{a}}:={\tilde{E}}]P\) discards a message if process P is able to discard the same message after applying attribute updates. Rule (FAware1) states that process \(\langle {\varPi }\rangle P\) discards a message even if \(\varPi \) evaluates to \((\mathsf{tt})\) if process P is able to discard the same message. Rule (FAware2) states that if \(\varPi \) in process \(\langle {\varPi }\rangle P\) evaluates to \(\mathsf{ff}\), process \(\langle {\varPi }\rangle P\) discards any message from other processes.
Rule (FZero) states that process \(\mathsf{0}\) always discards messages. Rule (FSum) states that process \(P_1 + P_2\) discards a message if both its subprocesses \(P_1\) and \(P_2\) can do so. Notice that the choice and awareness constructs do not dissolve after input refusal. Rule (FInt) has a similar meaning of Rule (FSum).
3.2 Operational Semantics of System
AbC system describes the global behavior of a component and the underlying communication between different components. We use the transition relation \(\xrightarrow {\ \ \ \ \ \ }{} \subseteq Comp\ \times \ SLAB\ \times \ Comp\) to define the behavior of a system where Comp denotes a component and SLAB is the set of transition labels \(\gamma \) which are generated by the following grammar:
The \(\gamma \)-labels extend \(\lambda \) with \(\tau \) to denote silent moves. The \(\tau \)-label has no free or bound names. The definition of the transition relation \(\xrightarrow {\ \ \ \ \ \ }{} \) depends on the definition of the relation  in the previous section in the sense that the effect of local behavior is lifted to the global one. The transition relation \(\xrightarrow {\ \ \ \ \ \ }{} \) is formally defined in Table 5. We omitted the symmetric rules for \(\tau \)
-Int and Com.
in the previous section in the sense that the effect of local behavior is lifted to the global one. The transition relation \(\xrightarrow {\ \ \ \ \ \ }{} \) is formally defined in Table 5. We omitted the symmetric rules for \(\tau \)
-Int and Com.
Rule (Comp) states that the relations  and \(\xrightarrow {\ \ \ \ \ \ }{}\) coincide when performing either an input or output action. Rule (C-Fail) states that any component \(\varGamma _{}\!:\!{P}\) can discard an input if its local process can do so. Rule (Rep) is standard for replication. Rule (\(\tau \)
-Int) models the interleaving between components \(C_1\) and \(C_2\) when performing a silent move (i.e., a send action \((\tilde{v})@{\varPi }\) with
and \(\xrightarrow {\ \ \ \ \ \ }{}\) coincide when performing either an input or output action. Rule (C-Fail) states that any component \(\varGamma _{}\!:\!{P}\) can discard an input if its local process can do so. Rule (Rep) is standard for replication. Rule (\(\tau \)
-Int) models the interleaving between components \(C_1\) and \(C_2\) when performing a silent move (i.e., a send action \((\tilde{v})@{\varPi }\) with  ). In this paper, we will use
). In this paper, we will use  to denote a silent action/move.
to denote a silent action/move.
Rule (Res) states that component \(\nu x C\) with a restricted name x can still perform an action with a \(\gamma \)-label as long as x does not occur in the names of the label and component C can perform the same action. If necessary, we allow renaming with conditions to avoid name clashing.
Rule (Sync) states that two parallel components \(C_1\) and \(C_2\) can synchronize while performing an input action. This means that the same message is received by both \(C_1\) and \(C_2\). Rule (Com) states that two parallel components \(C_1\) and \(C_2\) can communicate if \(C_1\) can send a message with a predicate that is different from \(\mathsf{ff}\) and \(C_2\) can possibly receive that message.
Rules (Hide1) and (Hide2) are peculiar to AbC and introduce a new concept that we call predicate restriction “\(\bullet \blacktriangleright x\)” as reported in Table 6. In process calculi with multiparty interaction like CSP [12] and \(b\pi \)-calculus [20], sending on a private channel is not observed. For example in \(b\pi \)-calculus, assume that \(P=\nu a(P_1 \Vert \ P_2)\Vert \ P_3\) where \(P_1=\bar{a}v.Q,\ P_2=a(x).R\), and \(\ P_3=b(x)\). Now if \(P_1\) sends on a then only \(P_2\) can observe it since \(P_2\) is included in the scope of the restriction. \(P_3\) and other processes only observe an internal action, so \(P\xrightarrow {\tau }\nu a(Q\Vert R[v/x])\Vert \ b(x)\).
This idea is generalized in AbC to what we call predicate restriction “\(\bullet \blacktriangleright x\)” in the sense that we either hide a part or the whole predicate using the predicate restriction operator “\(\bullet \blacktriangleright x\)” where x is a restricted name and the “\(\bullet \)” is replaced with a predicate. If the predicate restriction operator returns \(\mathsf{ff}\) then we get the usual hiding operator like in CSP and \(b\pi \)-calculus because the resulting label is not exposed according to (\(\tau \) -Int) rule (i.e., sending with a false predicate).
If the predicate restriction operator returns something different from \(\mathsf{ff}\) then the message is exposed with a smaller predicate and the restricted name remains private. Note that any private name in the message values (i.e., \(\tilde{x}\)) remains private if  as in rule (Hide1) otherwise it is not private anymore as in rule (Hide2). In other words, messages are sent on a channel that is partially exposed.
as in rule (Hide1) otherwise it is not private anymore as in rule (Hide2). In other words, messages are sent on a channel that is partially exposed.
For example, if a network sends a message with the predicate  where the name “fwd” is restricted then the message is exposed to users at every node within the network with forwarding capability with this predicate
where the name “fwd” is restricted then the message is exposed to users at every node within the network with forwarding capability with this predicate  . Network nodes observe the whole predicate but they receive the message only because they satisfy the other part of the predicate (i.e., \((capability=fwd)\)). In the following Lemma, we prove that the satisfaction of a restricted predicate \(\varPi \blacktriangleright x\) by an attribute environment \(\varGamma \) does not depend on the name x that is occurring in \(\varGamma \).
. Network nodes observe the whole predicate but they receive the message only because they satisfy the other part of the predicate (i.e., \((capability=fwd)\)). In the following Lemma, we prove that the satisfaction of a restricted predicate \(\varPi \blacktriangleright x\) by an attribute environment \(\varGamma \) does not depend on the name x that is occurring in \(\varGamma \).
Lemma 1
\(\varGamma \models \varPi \blacktriangleright x\ \) iff \(\ \forall v.\ \varGamma [v/x]\models \varPi \blacktriangleright x\ \) for any environment \(\varGamma \), predicate \(\varPi \), and name x.
Rule (Open) states that a component has the ability to communicate a private name to other components. The scope of the private name x only dissolves in the context where the rule is applied. Notice that, a component that is sending on a false predicate (i.e.,  ) cannot open the scope.
) cannot open the scope.
4 Expressiveness of AbC Calculus
In this section, we provide evidence of the expressive power of AbC by modeling systems featuring collaboration, adaptation, and reconfiguration and stress the possibility of using attribute-based communication as a unifying framework to encompass different communication models.
4.1 A Swarm Robotics Model in AbC
We consider a swarm of robots spreads in a given disaster area with the goal of locating and rescuing possible victims. All robots playing the same role execute the same code, defining their behavior, and a set of adaptation mechanisms, regulating the interactions among robots and their environments. Initially all robots are explorers and once a robot finds a victim, it changes its role to “rescuer” and sends victim’s information to nearby explorers. if another robot receives this information, it changes its role to “helper” and moves to join the rescuers-swarm. Notice that some of the robot attributes are considered as the projection of the robot internal state that is monitored by sensors and actuators (i.e., \(victimPerceived,\ position,\) and collision).
We assume that each robot has a unique identity (id) and since the robot acquires information about its environment or its own status by means of reading the values provided by sensors, no additional assumptions about the initial state are needed. It is worth mentioning that sensors and actuators are not modeled here as they represent the robot internal infrastructure while AbC model represents the programmable behavior of the robot (i.e., its running code).
The robotics scenario is modeled as a set of parallel AbC components, each component represents a robot (\(Robot_1 \Vert \dots \Vert Robot_n\)) and each robot has the following form \((\varGamma _{i}\!:\!{P_{R}})\). The behavior of a single robot is modeled in the following AbC process \(P_{R}\):

The robot follows a random walk in exploring the disaster arena. The robot can become a “Rescuer” when recognizing a victim by mean of locally reading the value of an attribute controlled by its sensors or stay as “explorer” and keep sending queries for information about the victim from nearby robots whose role is either “rescuer” or “helper”.
If a victim is perceived (i.e., the value of “\(victimPerceived=\mathsf{tt}\)”, the robot updates its “state” to “stop” which triggers halting the movement, computes the victim position and the number of the required robots to rescue the victim and stores them in the attributes “vPosition” and “count” respectively, changes its role to “rescuer”, and waits for queries from nearby explorers. Once a query is received, the robot sends back the victim information to the requesting robot addressing it by its identity “id” and the swarm starts forming.

If no victim is perceived, the robot keeps sending queries about victims to nearby robots whose role is either “rescuer” or “helper”. This query contains the robot identity “this.id”, a special name “qry” to indicate the request type, and the robot role “ ”. If an acknowledgement arrives containing victim’s information, the robot changes its role to “helper” and start the helping procedure.
”. If an acknowledgement arrives containing victim’s information, the robot changes its role to “helper” and start the helping procedure.

The helping robot stores the victim position in the attribute “vPosition” and updates its target to be the victim position. This triggers the actuators to move to the specified location. The robot waits until it reaches the victim and at the same time is willing to respond to other robots queries, if more than one robot is needed for the rescuing procedure. Once the robot reaches the victim, the robot changes its role to “rescuer” and joins the rescuer-swarm.

The “RandWalk” process is defined below. This process computes a random direction to be followed by the robot. Once a collision is detected by the proximity sensor, a new random direction is calculated.

For more details, a runtime environment for the linguistic primitives of AbC can be found in the following website http://lazkany.github.io/AbC.
4.2 Encoding Interaction Patterns
In this section, we show how group-based [1, 5, 13] and publish/subscribe-based [4, 9] interaction patterns can be naturally rendered in AbC. Since these interaction patterns do not have formal descriptions, we proceed by relying on examples.
We start with group-based interaction patterns and show that when modeling a group name as an attribute in AbC, the constructs for joining or leaving a given group can be modeled as attribute updates, see the following example:

initially \(\varGamma _1(group)=b\), \(\varGamma _2(group)=a\), and \(\varGamma _7(group)=c\). Component 1 wants to send the message “msg” to group “a”. Only Component 2 is allowed to receive it as it is the only member of group “a”. If Component 7 leaves group “c” and joins group “a” before “msg” is emitted then both of Component 2 and Component 7 will receive the message.
A possible encoding of group interaction into \(b\pi \)-calculus has been introduced in [8]. The encoding is relatively complicated and does not guarantee the causal order of message reception. “Locality” is neither a first class construct in \(b\pi \)-calculus nor in AbC. However, “locality” (in this case, the group name) can be modeled as an attribute in AbC while in \(b\pi \)-calculus, it needs much more effort.
Publish/subscribe interaction patterns can be considered as special cases of the attribute-based ones. For instance, a natural modeling of the topic-based publish/subscribe model [9] into AbC can be accomplished by allowing publishers to broadcast messages with “\(\mathsf{tt}\)” predicates (i.e., satisfied by all) and only subscribers can check the compatibility of the exposed publishers attributes with their subscriptions, see the following example:

The publisher broadcasts the message “msg” tagged with a specific topic for all possible subscribers (the predicate “\(\mathsf{tt}\)" is satisfied by all), subscribers receive the message if the topic matches their subscription.
5 Behavioral Theory for AbC
In this section, we define a behavioral theory for AbC. We start by introducing a barbed congruence, then we present an equivalent definition of bisimulation. In what follows, we shall use the following notations:
-
\(\Rightarrow \) denotes \( \xrightarrow {{\tau }}{^{*}}\ \ \) where \(\ \tau =\nu \tilde{x}\overline{\varPi }\tilde{v}\ \) with
 .
. -
 denotes
denotes  if \((\gamma \ne \tau )\).
if \((\gamma \ne \tau )\). -
 denotes
denotes  if \((\gamma =\tau ) \) and
if \((\gamma =\tau ) \) and  otherwise.
otherwise. -
 denotes \(\{\xrightarrow {\gamma }\ |\ \gamma \) is an output or \(\gamma =\tau \}\ \ \) and
denotes \(\{\xrightarrow {\gamma }\ |\ \gamma \) is an output or \(\gamma =\tau \}\ \ \) and 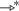 denotes
denotes 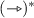 .
.
A context \(\mathcal {C}[\bullet ]\) is a component term with a hole, denoted by \([\bullet ]\) and AbC contexts are generated by the following grammar:
Barbed Congruence. We define notions of strong and weak barbed congruence to reason about AbC components following the definition of maximum sound theory by Honda and Yoshida [14]. This definition is a slight variant of Milner and Sangiorgi’s barbed congruence [21] and it is also known as open barbed bisimilarity [25].
Definition 2
(Barb). A predicate \(\varPi \)
Footnote 2 is observable (is a barb) in component C, denoted as \(C\downarrow _{\varPi }\), if C can send a message with a predicate \(\varPi ' \) (i.e., \(C\xrightarrow {\nu \tilde{x}\overline{\varPi ' }\tilde{v}}\) where  and
and  ). We write \(C\Downarrow _{\varPi }\) if
). We write \(C\Downarrow _{\varPi }\) if  .
.
Definition 3
(Barbed Congruence). A symmetric relation \(\mathcal {R}\) over the set of AbC components is a weak barbed congruence if whenever \((C_1, C_2)\in \mathcal {R}\),
-
\(C_1 \downarrow _{\varPi }\) implies \(C_2 \Downarrow _{\varPi }\);
-
 implies
implies  and \((C'_1, C'_2)\in \mathcal {R}\);
and \((C'_1, C'_2)\in \mathcal {R}\); -
for all contexts \(\mathcal {C}[\bullet ]\), \((\mathcal {C}[c_1], \mathcal {C}[c_2])\in \mathcal {R}\).
Two components are weak barbed congruent, written \(C_1 \cong C_2\), if \((C_1, C_2)\in \mathcal {R}\) for some barbed congruent relation \(\mathcal {R}\). The strong barbed congruence “\(\simeq \)” is obtained in a similar way by replacing \(\Downarrow \) with \(\downarrow \) and  with
with  .
.
Bisimulation. We define an appropriate notion of bisimulation for AbC components and prove that bisimilarity coincides with barbed congruence, and thus represents a valid tool for proving that two components are barbed congruent.
Definition 4
(Weak Bisimulation). A symmetric binary relation \(\mathcal {R}\) over the set of AbC components is a weak bisimulation if for every action \(\gamma \), whenever \((C_1, C_2)\in \mathcal {R}\) and \(\gamma \) is of the form \(\tau , \varPi (\tilde{v})\), or (\(\nu \tilde{x}\overline{\varPi }\tilde{v}\) with  ), it holds that:
), it holds that:

where every predicate \(\varPi \) occurring in \(\gamma \) is matched by its semantics meaning in \(\hat{\gamma }\). Two components \(C_1\) and \(C_2\) are weak bisimilar, written \(C_1 \approx C_2\) if there exists a weak bisimulation \(\mathcal {R}\) relating them. Strong bisimilarity, “\(\sim \)”, is defined in a similar way by replacing  with \(\xrightarrow {}\).
with \(\xrightarrow {}\).
Bisimilarity can be used as a reasoning tool and as a proof technique to compare systems at different levels of abstractions. For instance, the behavior of the robotic scenario in Sect. 4.1 can be compared with a centralized version where robots exchange information through a central node using an internet connection. Bisimilarity can also be used as a tool for state space reduction and minimization.
It is easy to prove that \(\sim \) and \(\approx \) are equivalence relations by relying on the classical arguments of [19]. However, our bisimilarity enjoys a much more interesting property: the closure under any context. So, in the next three lemmas, we prove that our bisimilarity is preserved by parallel composition, name restriction, and replication.
Lemma 2
( \(\sim \) and \(\approx \) are preserved by parallel composition). Let \(C_1\) and \(C_2\) be two components, then
-
\(C_1\sim C_2\) implies \(C_1\Vert C\ \sim \ C_2\Vert C\) for all components C
-
\(C_1\approx C_2\) implies \(C_1\Vert C\ \approx \ C_2\Vert C\) for all components C.
Lemma 3
( \(\sim \) and \(\approx \) are preserved by name restriction). Let \(C_1\) and \(C_2\) be two components, then
-
\(C_1\sim C_2\) implies \(\nu xC_1\ \sim \ \nu x C_2\) for all names x.
-
\(C_1\approx C_2\) implies \(\nu xC_1\ \approx \ \nu x C_2\) for all names x.
Lemma 4
( \(\sim \) and \(\approx \) are preserved by replication). Let \(C_1\) and \(C_2\) be two components, then
-
\(C_1\sim C_2\) implies \(!C_1\ \sim \ !C_2\)
-
\(C_1\approx C_2\) implies \(!C_1\ \approx \ !C_2\).
As an immediate consequence of Lemmas 2, 3, and 4, we have that \(\sim \) and \(\approx \) are congruence relations (i.e., closed under any context). We are now ready to show that our bisimilarity represents a proof technique for establishing barbed congruence. The proofs follow in a standard way.
Theorem 1
(Soundness). Let \(C_1\) and \(C_2\) be two components, then
-
\(C_1\sim C_2\) implies \(C_1\ \simeq \ C_2\)
-
\(C_1\approx C_2\) implies \(C_1\ \cong \ C_2\).
Lemma 5
(Completeness). Let \(C_1\) and \(C_2\) be two components, then
-
\(C_1\simeq C_2\) implies \(C_1\ \sim \ C_2\)
-
\(C_1\cong C_2\) implies \(C_1\ \approx \ C_2\).
Theorem 2
(Characterization). Bisimilarity and barbed congruence coincide.
6 Encoding Channel-Based Interaction
The interaction primitives in AbC are purely based on attributes rather than explicit names or channels. Attribute values can be locally modified. Modifying attribute values introduces opportunistic interactions between components by means of changing the set of possible interaction partners. The reason is because selecting interaction partners depends on the predicates over attributes and this is why modeling adaptivity in AbC is quite natural. This possibility is missing in channel-based communication since internal actions and the opportunity of interaction are orthogonal in those models.
We argue that finding a compositional encoding for the following simple behavior is very difficult if not impossible in channel-based process calculi.

Initially \(\varGamma _1(b)=3\) and \(\varGamma _2(a)=~2\). Changing the value of the local attribute a to “5” by the left-hand side process in the second component provides an opportunity of receiving the message “msg” from the first component.
On the other hand, in channel-based communication, a channel instantly appears at the time of interaction and disappears afterwards. This feature is not present in AbC since attributes are persistent in the attribute environment and cannot disappear at any time. However, this is not a problem in that we can exploit the fact that AbC predicates can check the received values. We simply add the channel name as a value in the message and the receiver checks its compatibility with its receiving channel.
To show the correctness of this encoding, we choose \(b\pi \)-calculus [8] as a representative for channel-based process calculi. The \(b\pi \)-calculus is a good choice because it is based on broadcast rather than binary communication which makes it a sort of variant of value-passing CBS [23]. Also, channels in \(b\pi \)-calculus can be communicated like in \(\pi \)-calculus [20]. We consider two level syntax for \(b\pi \)-calculus (i.e., only static contexts [19] are considered) as shown below.
Dealing with one level \(b\pi \)-syntax would not add difficulties related to channel encoding, but only related to the encoding of parallel composition and name restriction when occurring under a prefix or a choice. As reported in Table 7, the encoding of a \(b\pi \)-calculus process P is rendered as an AbC component  with \(\varGamma =\emptyset \). The channel is rendered as the first element in the sequence of values. For instance, in the output action \((a,\tilde{x})@(a=a)\), a represents the interaction channel, so the input action \( (y=a)(y,\tilde{x})\) will always check the first element of the received sequence to decide whether to accept or discard the message. Notice that the predicate \((a=a)\) is satisfied by any \(\varGamma \), however including the channel name in the predicate is crucial to encode name restriction correctly.
with \(\varGamma =\emptyset \). The channel is rendered as the first element in the sequence of values. For instance, in the output action \((a,\tilde{x})@(a=a)\), a represents the interaction channel, so the input action \( (y=a)(y,\tilde{x})\) will always check the first element of the received sequence to decide whether to accept or discard the message. Notice that the predicate \((a=a)\) is satisfied by any \(\varGamma \), however including the channel name in the predicate is crucial to encode name restriction correctly.
Now, we prove that the encoding is faithful, i.e., preserves the semantics of the original process. More precisely, we will prove the following Theorem:
Theorem 3
(Operational Correspondence). For any \(b\pi \) process P,
-
(Operational completeness): if
 then
then  .
. -
(Operational soundness): if
 then
then 
and
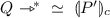 .
. -
(Barb preservation): both P and
 exhibit similar barbs i.e.,
exhibit similar barbs i.e.,\(P\downarrow _{b\pi }\) and
 .
.
The proof proceeds by induction on the shortest transition of \(\rightarrow _{b\pi }\). It shows that we can mimic each transition of \(b\pi \)-calculus by exactly one transition in \(AbC \). This implies that the completeness and the soundness of the operational correspondence can be even proved in a stronger way as in corollaries 1 and 2.
Corollary 1
(Strong Completeness). if  then \(\exists Q\) such that
then \(\exists Q\) such that  and
and  .
.
Corollary 2
(Strong Soundness). if  then
then  and
and 
As a result of Theorems 2 and 3 and of the strong formulations of Corollaries 1 and 2, this encoding is sound and complete with respect to bisimilarity as stated in the following corollaries.
Corollary 3
(Soundness w.r.t Bisimilarity).
-
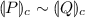 implies \(P\sim Q\)
implies \(P\sim Q\)
-
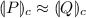 implies \(P \approx Q\).
implies \(P \approx Q\).
Corollary 4
(Completeness w.r.t Bisimilarity).
-
\(P\sim Q\) implies

-
\(P \approx Q\) implies
 .
.
7 Related Work
In this section, we report related works concerning languages and calculi with primitives that either model multiparty interaction or enjoy specific properties.
AbC is inspired by the SCEL language [6, 7] that was designed to support programming of autonomic computing systems [24]. Compared with SCEL, the knowledge representation in AbC is abstract and is not designed for detailed reasoning during the model evolution. This reflects the different objectives of SCEL and AbC. While SCEL focuses on programming issues, AbC concentrates on a minimal set of primitives to study attribute-based communication.
Many calculi that aim at providing tools for specifying and reasoning about communicating systems have been proposed: CBS [22] captures the essential features of broadcast communication in a simple and natural way. Whenever a process transmits a value, all processes running in parallel and ready to input catch the broadcast. The CPC calculus [11] relies on pattern-matching. Input and output prefixes are generalized to patterns whose unification enables a two-way, or symmetric, flow of information and partners are selected by matching inputs with outputs and testing for equality. The attribute \(\pi \)-calculus [16] aims at constraining interaction by considering values of communication attributes. A \(\lambda \)-function is associated to each receiving action and communication takes place only if the result of the evaluation of the function with the provided input falls within a predefined set of values. The imperative \(\pi \)-calculus [15] is a recent extension of the attribute \(\pi \)-calculus with a global store and with imperative programs used to specify constraints. The broadcast Quality Calculus of [27] deals with the problem of denial-of-service by means of selective input actions. It inspects the structure of messages by associating specific contracts to inputs, but does not provide any mean to change the input contracts during execution.
AbC combines the learnt lessons from the above mentioned languages and calculi in the sense that AbC strives for expressivity while preserving minimality and simplicity. The dynamic settings of attributes and the possibility of inspecting/modifying the environment gives AbC greater flexibility and expressivity while keeping models as much natural as possible.
8 Concluding Remarks
We have introduced a foundational process calculus, named AbC, for attribute-based communication. We investigated the expressive power of AbC both in terms of its ability to model scenarios featuring collaboration, reconfiguration, and adaptation and of its ability to encode channel-based communication and other interaction paradigms. We defined behavioral equivalences for AbC and finally we proved the correctness of the proposed encoding up to some reasonable equivalence. We demonstrated that the general concept of attribute-based communication can be exploited to provide a unifying framework to encompass different communication models. We developed a centralized prototype implementation for AbC linguistic primitives to demonstrate their simplicity and flexibility to accommodate different interaction patterns.
We plan to investigate the impact of bisimulation in terms of axioms, proof techniques, etc. for working with the calculus and to consider alternative behavioral relations like testing preorders.
Another line of research is to investigate anonymity at the level of attribute identifiers. Clearly, AbC achieves dynamicity and openness in the distributed settings, which is an advantage compared to channel-based models. In our model, components are anonymous, however the “name-dependency” challenge arises at another level, that is, the attribute environments. In other words, the sender’s predicate should be aware of the identifiers of receiver’s attributes in order to explicitly use them. For instance, the sending predicate \((loc=<1,4>)\) targets the components at location \(<1,4>\), however, different components might use different identifiers to denote their locations; this requires that there should be an agreement about the attribute identifiers used by the components. For this reason, appropriate mechanisms for handling attribute directories together with identifiers matching/correspondence will be considered. These mechanisms will be particularly useful when integrating heterogeneous applications.
Further attention will be also dedicated to provide an efficient distributed implementation for AbC linguistic primitives. We also plan to investigate the effectiveness of AbC not only as a tool for encoding calculi but also for dealing with case studies from different application domains.
Notes
- 1.
Occasionally, we will use “attribute” to denote “attribute identifier” in this paper.
- 2.
From now on, we use the predicate \(\varPi \) to denote only its meaning, not its syntax.
References
Agha, G., Callsen, C.J.: ActorSpace: an open distributed programming paradigm, vol. 28. ACM (1993)
Alrahman, Y.A., De Nicola, R., Loreti, M.: On the power of attribute-based communication, extended report (2016)
Alrahman, Y.A., De Nicola, R., Loreti, M., Tiezzi, F., Vigo, R.: A calculus for attribute-based communication. In: Proceedings of the 30th Annual ACM Symposium on Applied Computing, SAC 2015, pp. 1840–1845. ACM (2015)
Bass, M.A., Nguyen, F.T.: Unified publish and subscribe paradigm for local and remote publishing destinations, US Patent 6,405,266, 11 June 2002
Chockler, G.V., Keidar, I., Vitenberg, R.: Group communication specifications: a comprehensive study. ACM Comput. Surv. 33, 427–469. ACM (2001). doi:10.1145/503112.503113
De Nicola, R., Ferrari, G., Loreti, M., Pugliese, R.: A language-based approach to autonomic computing. In: Boer, F.S., Bonsangue, M.M., Beckert, B., Damiani, F. (eds.) FMCO 2011. LNCS, vol. 7542, pp. 25–48. Springer, Heidelberg (2012)
De Nicola, R., Loreti, M., Pugliese, R., Tiezzi, F.: A formal approach to autonomic systems programming: the scel language. ACM Trans. Auton. Adapt. Syst. 9, 1–29 (2014)
Ene, C., Muntean, T.: A broadcast-based calculus for communicating systems. In: Parallel and Distributed Processing Symposium, International, vol. 3, p. 30149b. IEEE Computer Society (2001)
Eugster, P.T., Felber, P.A., Guerraoui, R., Kermarrec, A.-M.: The many faces of publish/subscribe. ACM Comput. (CSUR) 35(2), 114–131 (2003)
Ferscha, A.: Collective adaptive systems. In: Proceedings of the 2015 ACM International Joint Conference on Pervasive and Ubiquitous Computing and Proceedings of the 2015 ACM International Symposium on Wearable Computers, pp. 893–895 (2015)
Given-Wilson, T., Gorla, D., Jay, B.: Concurrent pattern calculus. In: Calude, C.S., Sassone, V. (eds.) TCS 2010. IFIP AICT, vol. 323, pp. 244–258. Springer, Heidelberg (2010)
Antony Richard Hoare, C.: Communicating sequential processes. Commun. ACM 21(8), 666–677 (1978)
Holbrook, H.W., Cheriton, D.R.: Ip multicast channels: express support for large-scale single-source applications. In: ACM SIGCOMM Computer Communication Review, vol. 29, pp. 65–78. ACM (1999)
Honda, K., Yoshida, N.: On reduction-based process semantics. Theor. Comput. Sci. 151(2), 437–486 (1995)
John, M., Lhoussaine, C., Niehren, J.: Dynamic compartments in the imperative \(\pi \)-calculus. In: Degano, P., Gorrieri, R. (eds.) CMSB 2009. LNCS, vol. 5688, pp. 235–250. Springer, Heidelberg (2009)
John, M., Lhoussaine, C., Niehren, J., Uhrmacher, A.M.: The attributed Pi-calculus with priorities. In: Priami, C., Breitling, R., Gilbert, D., Heiner, M., Uhrmacher, A.M. (eds.) Transactions on Computational Systems Biology XII. LNCS, vol. 5945, pp. 13–76. Springer, Heidelberg (2010)
Mamei, M., Zambonelli, F.: Programming pervasive and mobile computing applications with the tota middleware. In: Proceedings of the Second IEEE Annual Conference on Pervasive Computing and Communications, 2004. PerCom 2004, pp. 263–273. IEEE (2004)
Milner, R. (ed.): A Calculus of Communication Systems. LNCS, vol. 92. Springer, Heidelberg (1980). doi:10.1007/3-540-10235-3
Milner, R.: Communication and Concurrency. Prentice-Hall Inc, Upper Saddle River (1989)
Milner, R., Parrow, J., Walker, D.: A calculus of mobile processes, ii. Inf. Comput. 100(1), 41–77 (1992)
Milner, R., Sangiorgi, D.: Barbed bisimulation. In: Kuich, W. (ed.) ICALP 1992. LNCS, vol. 623, pp. 685–695. Springer, Heidelberg (1992)
Prasad, K.V.S.: A calculus of broadcasting systems. Sci. Comput. Program. 25(2), 285–327 (1995)
Prasad, K.V.S.: A calculus of broadcasting systems. In: Abramsky, S. (ed.) CAAP 1991 and TAPSOFT 1991. LNCS, vol. 493, pp. 338–358. Springer, Heidelberg (1991)
Sanders, J.W., Smith, G.: Formal ensemble engineering. In: Wirsing, M., Banâtre, J.-P., Hölzl, M., Rauschmayer, A. (eds.) Software-Intensive Systems. LNCS, vol. 5380, pp. 132–138. Springer, Heidelberg (2008)
Sangiorgi, D., Walker, D.: The pi-calculus: A Theory of Mobile Processes. Cambridge University Press, Cambridge (2003)
Sommerville, I., Cliff, D., Calinescu, R., Keen, J., Kelly, T., Kwiatkowska, M., Mcdermid, J., Paige, R.: Large-scale complex it systems. Commun. ACM 55(7), 71–77 (2012)
Vigo, R., Nielson, F., Nielson, H.R.: Broadcast, denial-of-service, and secure communication. In: Johnsen, E.B., Petre, L. (eds.) IFM 2013. LNCS, vol. 7940, pp. 412–427. Springer, Heidelberg (2013)
Viroli, M., Damiani, F., Beal, J.: A calculus of computational fields. In: Canal, C., Villari, M. (eds.) Advances in Service-Oriented and Cloud Computing, pp. 114–128. Springer, Heidelberg (2013)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 IFIP International Federation for Information Processing
About this paper
Cite this paper
Abd Alrahman, Y., De Nicola, R., Loreti, M. (2016). On the Power of Attribute-Based Communication. In: Albert, E., Lanese, I. (eds) Formal Techniques for Distributed Objects, Components, and Systems. FORTE 2016. Lecture Notes in Computer Science(), vol 9688. Springer, Cham. https://doi.org/10.1007/978-3-319-39570-8_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-39570-8_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-39569-2
Online ISBN: 978-3-319-39570-8
eBook Packages: Computer ScienceComputer Science (R0)





 .
. denotes
denotes  if
if  denotes
denotes  if
if  otherwise.
otherwise. denotes
denotes 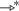 denotes
denotes 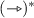 .
. implies
implies  and
and  then
then  .
. then
then 
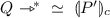 .
. exhibit similar barbs i.e.,
exhibit similar barbs i.e., .
.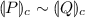 implies
implies 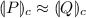 implies
implies 
 .
.