Abstract
Witness encryption (WE) was introduced by Garg et al. [GGSW13]. A WE scheme is defined for some NP language L and lets a sender encrypt messages relative to instances x. A ciphertext for x can be decrypted using w witnessing \(x\in L\), but hides the message if \(x\notin L\). Garg et al. construct WE from multilinear maps and give another construction [GGH+13b] using indistinguishability obfuscation (iO) for circuits. Due to the reliance on such heavy tools, WE can currently hardly be implemented on powerful hardware and will unlikely be realizable on constrained devices like smart cards any time soon.
We construct a WE scheme where encryption is done by simply computing a Naor-Yung ciphertext (two CPA encryptions and a NIZK proof). To achieve this, our scheme has a setup phase, which outputs public parameters containing an obfuscated circuit (only required for decryption), two encryption keys and a common reference string (used for encryption). This setup need only be run once, and the parameters can be used for arbitrary many encryptions. Our scheme can also be turned into a functional WE scheme, where a message is encrypted w.r.t. a statement and a function f, and decryption with a witness w yields f(m, w).
Our construction is inspired by the functional encryption scheme by Garg et al. and we prove (selective) security assuming iO and statistically simulation-sound NIZK. We give a construction of the latter in bilinear groups and combining it with ElGamal encryption, our ciphertexts are of size 1.3 kB at a 128-bit security level and can be computed on a smart card.
Research supported by the European Research Council, ERC starting grant (259668-PSPC) and ERC consolidator grant (682815 - TOCNeT).
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Witness Encryption. In an encryption scheme, the receiver needs to know some secret piece of information (the secret key) to decrypt. Garg, Gentry, Sahai and Waters [GGSW13] propose the intriguing new notion of witness encryption (WE), where a scheme is defined for some NP language L with witness relation R: \(L=\{x\,|\exists \,w:R(x,w)=1\}\). The encryption algorithm takes an instance x (instead of a public key) and a message m and produces a ciphertext c. Using a witness w such that \(R(x,w)=1\), anyone can decrypt ciphertext c. Decryption is only possible if x is actually in the language and it is required that a ciphertext computed for some \(x\not \in L\) computationally hides the message m.
Applications. As shown in [GGSW13], from WE one can construct powerful cryptographic primitives such as identity-based encryption and attribute-based encryption [SW05] for circuits. But WE also allows for applications that were not possible before; for example, one can encrypt a message with respect to a puzzle, such that only someone who found a solution can decrypt. This puzzle can be any problem where solutions can be efficiently verified, like a crossword or Sudoku puzzle, or even the proof for some mathematical conjecture. Another application is asymmetric password-based encryption [BH15], which allows hashed passwords (for any password-hashing function already in place) to be used as public encryption keys and passwords to decrypt.
Constructing WE. Garg et al. [GGSW13] construct a WE scheme for the NP-complete language “exact set cover”, which implies WE for any language \(L\in \text {NP}\) via polynomial-time many-one reductions (a.k.a. Levin reductions). The security of this construction is based on a strong assumption on “approximate” multilinear maps as constructed in [GGH13a]. Subsequently, a construction of WE from indistinguishability obfuscation (iO) was given in [GGH+13b] and another one based on multilinear maps in [GLW14]. The only candidate construction of iO is also based on the approximate multilinear maps from [GGH13a].
Implementing multilinear maps as required for iO or WE is computationally very expensive, but a first—though far from practical—implementation exists [AHKM14], and it is conceivable that algorithmic and hardware progress yield practical implementations in the not too distant future.
Offline Witness Encryption. Given that WE is not even practical on high-end machines, it seems foolish to hope for an implementation on low-end devices like smart cards. In this paper we show however that it is possible to construct a WE scheme where encryption is very efficient, as the entire computationally hard work can be moved to a setup phase and—to a lesser extent—to the decryption process. This setup is either run by the sender before she knows the instance and the message for an encryption; or it is run by a trusted party once and for all and everyone can use the same parameters. The first case is reminiscent of online/offline encryption or signatures [EGM96], except that in our case, once generated, the parameters can be used for arbitrary many “online phases”.
We call this concept offline witness encryption and define it as a tuple of three algorithms. The setup phase (which is not present in standard WE) takes as input only a security parameter \(1^\lambda \) and outputs public parameters  . To encrypt a message m for an instance x, one runs an encryption algorithm
. To encrypt a message m for an instance x, one runs an encryption algorithm  . Such ciphertext c can then be decrypted given a witness w, i.e., for which \(R(x,w)=1\) holds, as
. Such ciphertext c can then be decrypted given a witness w, i.e., for which \(R(x,w)=1\) holds, as  . The goal of offline WE is to keep the parameters
. The goal of offline WE is to keep the parameters  for encryption and ciphertexts small and the \(\mathsf{Enc }\) algorithm efficient.
for encryption and ciphertexts small and the \(\mathsf{Enc }\) algorithm efficient.
Applications of Offline WE. In any application of witness encryption its offline variant can be used to make encryption practically efficient, if one accepts an additional setup phase. However, for applications like IBE and attribute-based encryption, as discussed in [GGSW13], system-wide parameters must be set up by a trusted party anyway. This party could therefore simply also generate the offline-WE parameters, meaning encryption can be made efficient without requiring any additional trust.
Bellare and Tung Hoang [BH15] define and construct asymmetric password-based encryption (A-PBE), where a hash of a password can be used as a public key to encrypt messages, which can then be decrypted using the password. Unlike its symmetric counterpart, A-PBE remains secure even when the server storing hashed passwords is compromised. In particular, they show that if hashed passwords are already deployed using an existing password-hashing function, witness encryption can be used to turn the hashed passwords into public keys.Footnote 1 The drawback of using WE is that both encryption and decryption are inefficient. Using offline WE where a trusted third party produces the system parameters in an offline phase, encryption can be made significantly more efficient, whereas decryption (and the one-time setup) remains inefficient.
The use of offline WE is therefore particularly appealing in scenarios where decryption is usually not done anyway, but ciphertexts are made public as a means of deterrent. Consider a scenario where a content provider lets subscribed users set up passwords and use them to access some content. The provider typically stores a hash of the password. In order to discourage subscribers from distributing their passwords and allowing others to access content, the provider could simply encrypt some sensitive user information (such as credit card details, etc.) under a user’s hashed password and publish this ciphertext. As anyone who knows the password could decrypt, it is then in the user’s interest to keep his password secret.
Our Construction. Our construction, as well as its proof, is inspired by the functional encryption scheme by Garg et al. [GGH+13b].
The parameters required for encryption  consist of two public keys of a standard public-key encryption (PKE) scheme and a common reference string for a non-interactive zero-knowledge (NIZK) proof system. The encryption \(c=(x,c_1,c_2,\pi )\) of a message m for an instance x is simply a Naor-Yung [NY90, Sah99] CCA-secure encryption of the pair (x, m); that is, encryptions \(c_1\) and \(c_2\) of (x, m) under
consist of two public keys of a standard public-key encryption (PKE) scheme and a common reference string for a non-interactive zero-knowledge (NIZK) proof system. The encryption \(c=(x,c_1,c_2,\pi )\) of a message m for an instance x is simply a Naor-Yung [NY90, Sah99] CCA-secure encryption of the pair (x, m); that is, encryptions \(c_1\) and \(c_2\) of (x, m) under  and
and  , respectively, together with a NIZK proof \(\pi \) showing that the two ciphertext \(c_1,c_2\) encrypt the same message.
, respectively, together with a NIZK proof \(\pi \) showing that the two ciphertext \(c_1,c_2\) encrypt the same message.
The setup algorithm samples two key pairs \((\textit{sk}_1,\textit{pk}_1)\), \((\textit{sk}_2,\textit{pk}_2)\) for the PKE scheme and a CRS for the NIZK proof system. The parameters  required for decryption consist of the obfuscation \(\tilde{D}\) of a circuit D defined as follows. On input a ciphertext \(c=(x,c_1,c_2,\pi )\) and a string w, the circuit D
required for decryption consist of the obfuscation \(\tilde{D}\) of a circuit D defined as follows. On input a ciphertext \(c=(x,c_1,c_2,\pi )\) and a string w, the circuit D
-
checks if \(R(x,w)=1\) (i.e., w is a witness for \(x\in L\));
-
checks if \(\pi \) is a proof that \(c_1\) and \(c_2\) encrypt the same message; and
-
if both checks pass, decrypts \((x',m)=\mathsf{PK.Dec }(\textit{sk}_1,c_1)\) and outputs m if \(x'=x\).
Given an (obfuscated) circuit as above, the decryption algorithm of our WE scheme simply evaluates \(\tilde{D}((x,c_1,c_2,\pi ),w)\), which will output the message m for any witness w with \(R(x,w)=1\).
We prove in Theorem 1 that the above is a secure offline-WE scheme (meaning that ciphertexts for \(x\not \in L\) computationally hide the message), assuming that the obfuscation satisfies the notion of indistinguishability obfuscation [BGI+01], the NIKZ is statistically simulation-sound [GGH+13b] and the PKE is semantically secure under chosen-plaintext attack (CPA).
Functional Witness Encryption. Functional witness encryption was proposed by Boyle et al. [BCP14] and its encryption algorithm takes as input a circuit f in addition to instance x and message m. A party knowing a witness w for x now does not learn m itself, but only the function f(m, w). For example, x could be a labeled graph and a party knowing a t-clique in x can learn the labels of this clique (but no other labels). Indistinguishability-based security (there is also an extractability-based notion) requires that, even when \(x\in L\), encryptions of \((x,m_0,f_0)\) and \((x,m_1,f_1)\) are indistinguishable if for all w with \(R(x,w)=1\) we have \(f_0(m_0,w)=f_1(m_1,w)\).
In Sect. 4 we define an offline variant of functional witness encryption and give an instantiation by adapting the (obfuscated) decryption circuit of our OWE scheme: instead of outputting m when given a witness w, it parses m as a pair \((f,m')\) and outputs \(f(m',w)\). Encryption still consists of computing a Naor-Yung ciphertext, whereas for the scheme in [BCP14] the encryptor needs to perform iO-obfuscation.
Efficiency of Encryption. In Sect. 5 we propose a concrete instantiation of the encryption algorithm used by our OWE schemes. In order to avoid random oracles, we use Groth-Sahai proofs [GS08], which are perfectly sound NIZK proofs in the standard model for languages defined over bilinear groups. They let us prove that two ElGamal ciphertexts encrypt the same message. Using ideas from [GGH+13b] and making them efficient by translating them into the bilinear-group framework, we construct a statistically simulation-sound (SSS) proof system. Under the so-called SXDH assumption (which states that the decisional Diffie-Hellman problem holds in the base groups), the encryption scheme is CPA-secure and the proof system we construct is zero-knowledge.
In our instantiation a proof consists of 28 elements from a bilinear group and is computed by using bilinear-group exponentiations (but no pairings). For a 128-bit security level, the size of the output of our encryption algorithm, comprising 2 ciphertexts and one SSS proof, is about 1.3 kB.
Handling Long Messages and Instances. ElGamal encryption is defined over a group \(\mathbb {G}\) and encrypts elements from \(\mathbb {G}\); we therefore need to encode the message (x, m) into \(\mathbb {G}\). Using elliptic-curve-based groups, for 128-bit security the length of an element from \(\mathbb {G}\) is 256 bits, and standard encoding techniques [FJT13] allow for encoding of 128 bits into one group element, which is prohibitively small for any meaningful application.
We could of course choose a larger group such that one group element fits the entire tuple (x, m), but this would become very inefficient for large values. The encryption procedure we construct in Sect. 5 will therefore allow to encrypt arbitrarily long messages by encrypting them block-wise. We then need to provide a proof for each 128-bit block separately; however, using some optimization, we manage to limit the growth of the ciphertext to 0.25 kB for every 128 bits of plaintext, meaning the ciphertext grows by a factor of 16 compared to the plaintext.
For offline WE (but not for its functional variant) a further optimization when handling large messages m is to use key encapsulation: when encrypting, the sender first picks a key k for a symmetric encryption scheme and generates a ciphertext \(c=(c_K,c_M)\), where \(c_K\) is the WE encryption of (x, k), and \(c_M\) is the (secret-key) encryption of m under k. To decrypt (given a witness w), the receiver first decrypts \(c_K\) to learn k and then decrypts \(c_M\) to recover m.
Dealing with large instances x turns out more tricky. Instead of x we could encrypt a hash \(y=H(x)\) using a collision-resistant hash function H, noting that x is input to the decryption algorithm, which can therefore check whether \(y=H(x)\). However, to prove this construction secure, we require the notion of differing-inputs obfuscation (a.k.a. extractability obfuscation) [BGI+01, BCP14, ABG+13], which seems a much stronger assumption than indistinguishability obfuscation, as implausibility results in [GGHW14] show.
Related Work. Zhandry [Zha14] proposes the notion of reusable witness encryption, which is similar to offline WE. Apart from being a key-encapsulation scheme (which does not generalize to FWE), the main difference is that setup outputs parameters which are used for both encryption and decryption and additionally a master decryption key (which allows for CCA-type security).
Zhandry constructs reusable WE using multilinear maps (and no obfuscation), which makes decryption more efficient than ours. Although ciphertexts in [Zha14] are short, the parameters are not, and, more importantly, encryption is less efficient than ours as it requires the evaluation of a multilinear map whose level of multilinearity is linear in the number of gates of the circuit describing the NP relation R. Efficient encryption was our main motivation for introducing offline WE and for this reason our model has separate parameters for encryption and decryption.
2 Preliminaries
2.1 Notations and Conventions
Families of Circuits. A family of circuits \(\{\mathcal{C}_\lambda \}_{\lambda \in \mathbb {N}}\) is of polynomial size if for some polynomial \(p(\cdot )\) the size of every \(C \in \mathcal{C}_\lambda \) is at most \(|C|\le p(\lambda )\).
Probabilistic Algorithms. If \(\mathcal{X}\) is a finite set then \(x \leftarrow \mathcal{X}\) denotes the process of sampling x uniformly at random from \(\mathcal{X}\). Let \(\mathcal{A}\) be a probabilistic polynomial-time (PPT) algorithm; then \(\Pr [y \leftarrow \mathcal{A}(x)]\) denotes the probability that \(\mathcal{A}(x)\) outputs y when run on uniformly sampled coins. We let \(\Pr \big [ x_1 \leftarrow \mathcal{X}_1 ;x_2 \leftarrow \mathcal{X}_2;\ldots \ :\ \varphi (x_1,x_2, \ldots )=1\big ]\) denote the probability that the predicate \(\varphi \) evaluated on \((x_1,x_2, \ldots )\) is true after the ordered execution of \(x_1 \leftarrow \mathcal{X}_1\), \(x_2 \leftarrow \mathcal{X}_2, \ldots \)
Negligible Functions. A function \(\nu :\mathbb {N}\rightarrow \mathbb {R}\) is called negligible if for every positive polynomial \(p(\cdot )\), and all sufficiently large \(n \in \mathbb {N}\), it holds that \(\nu (n) \le \frac{1}{p(n)}\). We write  to mean that \(f(\cdot )\) is negligible.
to mean that \(f(\cdot )\) is negligible.
2.2 Public-Key Encryption
Our first ingredient is a standard public-key encryption scheme.
Definition 1
(PKE). A public-key encryption scheme for a message space \(\mathcal{M}\) is a tuple of PPT algorithms  .
.  , on input a security parameter \(1^\lambda \), outputs a secret/public key pair
, on input a security parameter \(1^\lambda \), outputs a secret/public key pair  .
.  , on input a public key
, on input a public key  and a message \(m\in \mathcal{M}\), outputs a ciphertext c using randomness
and a message \(m\in \mathcal{M}\), outputs a ciphertext c using randomness  . Finally,
. Finally,  , on input a secret key \(\textit{sk}\) and a ciphertext c, outputs
, on input a secret key \(\textit{sk}\) and a ciphertext c, outputs  . Furthermore we require correctness and security:
. Furthermore we require correctness and security:
-
Correctness: For every \(\lambda \in \mathbb {N}\), \(m\in \mathcal{M}\) we have

-
Indistinguishability under chosen-plaintext attacks (CPA): For every non-uniform PPT adversary
 in
in  (Fig. 1) we have
(Fig. 1) we have 
2.3 Indistinguishability Obfuscation
As a consequence of the impossibility of virtual black-box obfuscation, Barak et al. [BGI+12] proposed the weaker notion of indistinguishability obfuscation (iO), which guarantees that obfuscations of equivalent functionalities are computationally indistinguishable.
Definition 2
(Indistinguishability obfuscation [BGI+12, GGH+13b]). A uniform PPT algorithm \(i\mathcal O\) is an indistinguishability obfuscator for a family of polynomial-size circuits \(\{\mathcal{C}_\lambda \}_{\lambda \in \mathbb {N}}\), if the following hold:
-
For all \(\lambda \in \mathbb {N}\), \(C \in \mathcal{C}_\lambda \), \(x\in \{0,1\}^\lambda \): \(\Pr \big [\widetilde{C} \leftarrow i\mathcal O(1^\lambda , C): C(x)=\widetilde{C}(x)]=1\).
-
For every non-uniform PPT adversary \(\mathcal{A}\), there exists a negligible function \(\nu (\cdot )\) such that for all \(C_0,C_1 \in \mathcal{C}_\lambda \) such that \(C_0(x)=C_1(x)\) for all x:
$$\begin{aligned} \big |\Pr \big [\mathcal{A}(i\mathcal O(1^\lambda ,C_0))=1\big ]-\Pr \big [\mathcal{A}(i\mathcal O(1^\lambda ,C_1))=1\big ]\big | = \nu (\lambda ). \end{aligned}$$(1)
Garg et al. [GGH+13b] provide a candidate iO construction for families of polynomial-size circuits.
2.4 Statistically Simulation-Sound NIZK
A non-interactive (NI) proof system for a language  consists of four PPT algorithms: a common-reference string (CRS) generator \(\mathsf{G }\), which on input \(1^\lambda \) outputs a CRS; a prover \(\mathsf{P }\), which on input a CRS, a statement y and a witness w outputs a proof; and a verifier \(\mathsf{V }\), which on input a CRS, a statement and a proof outputs 0 or 1.
consists of four PPT algorithms: a common-reference string (CRS) generator \(\mathsf{G }\), which on input \(1^\lambda \) outputs a CRS; a prover \(\mathsf{P }\), which on input a CRS, a statement y and a witness w outputs a proof; and a verifier \(\mathsf{V }\), which on input a CRS, a statement and a proof outputs 0 or 1.
We require a proof system that satisfies completeness, statistical soundness, and zero-knowledge (ZK). Completeness means that, on input a statement and a witness, \(\mathsf{P }\) outputs a proof that \(\mathsf{V }\) accepts. Statistical soundness requires that no unbounded adversary can produce a proof of a false statement. Zero-knowledge means that a proof does not reveal any information (in a computational sense) about the witness used to compute it; this is formalized by requiring the existence of a simulator \(\mathsf{{S}}=(\mathsf{S_1 },\mathsf{S_2 })\) that can output a CRS and a proof for any statement, which are computationally indistinguishable from real ones.
A NIZK proof system is statistically simulation-sound (SSS) [GGH+13b] if no unbounded adversary can produce a valid proof for a statement \(y' \notin L\) even when given a simulated proof for any other statement \(y \ne y'\).
Definition 3
(SSS-NIZK). A tuple of PPT algorithms \((\mathsf{G }, \mathsf{P },\mathsf{V },\mathsf{{S}}=(\mathsf{S_1 },\mathsf{S_2 }))\) is a statistically simulation-sound non-interactive zero-knowledge (SSS-NIZK) proof system for  with witness relation R if the following hold:
with witness relation R if the following hold:
-
Perfect completeness: For every (y, w) such that \(R(y,w)=1\), it holds that
$$\begin{aligned} \Pr \big [\textit{crs}\leftarrow \mathsf{G }(1^\lambda )\,;\, \pi \leftarrow \mathsf{P }(\textit{crs}, y, w)\ :\ \mathsf{V }(\textit{crs},y,\pi )=1\big ] =1 .\end{aligned}$$ -
Statistical soundness:
$$\begin{aligned} \Pr \big [\textit{crs}\leftarrow \mathsf{G }(1^\lambda )\ :\ \begin{array}{r}\exists \, (y, \pi ) ~\text {s.t.}~ y\notin L \,\wedge \, \mathsf{V }(\textit{crs}, y,\pi )=1\end{array}\big ] = \mathsf{negl}(\lambda ) .\end{aligned}$$ -
Computational zero-knowledge: For every (y, w) such that \(R(y,w)=1\), and non-uniform PPT adversary \(\mathcal{A}\), it holds that
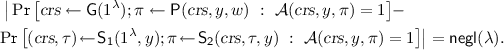 (2)
(2) -
Statistical simulation soundness: For every y, it holds that
$$\begin{aligned} \Pr \left[ \begin{array}{l} (\textit{crs},\tau ) \leftarrow \mathsf{S_1 }(1^\lambda ,y); \\ \pi \leftarrow \mathsf{S_2 }(\textit{crs},\tau ,y) \end{array}\ :\ \begin{array}{l}\exists \, (y', \pi ') ~\text {s.t.}~ y' \ne y \wedge y'\notin L \\ \wedge \ \mathsf{V }(\textit{crs}, y',\pi ')=1\end{array}\right] = \mathsf{negl}(\lambda ) .\end{aligned}$$(3)
Garg et al. [GGH+13b] construct an SSS-NIZK scheme from any statistically sound NIZK scheme and any computationally hiding and perfectly binding non-interactive commitment scheme. In Sect. 5, we give an efficient instantiation of this, following their blueprint and using perfectly sound Groth-Sahai proofs [GS08] and ElGamal encryption as perfectly binding and computationally hiding commitment scheme. In particular, our SSS-NIZK proof system is for the following NP language.
Definition 4
Let \((\mathsf{PK.Gen }, \mathsf{PK.Enc }, \mathsf{PK.Dec })\) be a public-key encryption scheme. We define the \(\mathsf{NP }\) language \( L_\mathsf{{enc}}\) and let \( R_\mathsf{{enc}}\) denote its witness relation:
3 Offline Witness Encryption
A (standard) witness encryption scheme [GGSW13, BH15] is defined by an encryption algorithm \(\mathsf{Enc }\) that takes a security parameter \(1^\lambda \), a statement x and a message m and outputs a ciphertext c; and a decryption algorithm \(\mathsf{Dec }\) that on input a ciphertext c and a witness w outputs a message. Offline witness encryption allows for efficient encryption by outsourcing the resource-heavy computations to a setup phase, which is independent of the statement and message to be encrypted. There is a third algorithm  which on input a security parameter \(1^\lambda \) outputs a pair of parameters:
which on input a security parameter \(1^\lambda \) outputs a pair of parameters:  , which is used by
, which is used by  , and
, and  , which is used by
, which is used by  . In our formalization we follow the strengthened definition of witness encryption put forth by Bellare and Tung Hoang [BH15].
. In our formalization we follow the strengthened definition of witness encryption put forth by Bellare and Tung Hoang [BH15].
Definition 5
(Offline witness encryption). An offline witness encryption (OWE) scheme for a language  with witness relation
with witness relation  is a tuple of PPT algorithms \(\mathsf{OWE}=(\mathsf{Setup }, \mathsf{Enc }, \mathsf{Dec })\) where:
is a tuple of PPT algorithms \(\mathsf{OWE}=(\mathsf{Setup }, \mathsf{Enc }, \mathsf{Dec })\) where:
-
 : On input a security parameter \(1^\lambda \), Setup outputs parameters for encryption
: On input a security parameter \(1^\lambda \), Setup outputs parameters for encryption  and parameters for decryption
and parameters for decryption  .
. -
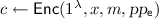 : On input a security parameter \(1^\lambda \), a string \(x\in \mathcal{X}\), a message \(m \in \mathcal{M}\), and encryption parameters
: On input a security parameter \(1^\lambda \), a string \(x\in \mathcal{X}\), a message \(m \in \mathcal{M}\), and encryption parameters  , Enc outputs a ciphertext c.
, Enc outputs a ciphertext c. -
 : On input a ciphertext c, a string
: On input a ciphertext c, a string  and decryption parameters
and decryption parameters 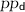 , Dec outputs
, Dec outputs 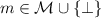 .
.
We require correctness and security:
-
Correctness: For all
 such that \(R(x,w)=1\), \(m\in \mathcal{M}\):
such that \(R(x,w)=1\), \(m\in \mathcal{M}\): 
-
Security: \(\mathsf{OWE}\) is selectively secure if for every non-uniform PPT adversary
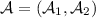 in
in  (Fig. 2) it holds that
(Fig. 2) it holds that 
\(\mathsf{OWE}\) is adaptively secure if the same holds for
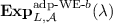 (Fig. 3).
(Fig. 3).
We now present our construction of offline WE that we have outlined in the introduction and prove that it satisfies selective security.
Construction 1
(Offline WE). Let  be a public-key encryption scheme,
be a public-key encryption scheme,  an SSS-NIZK scheme for \( L_\mathsf{{enc}}\) (Definition 4), and \(i\mathcal O\) an indistinguishability obfuscator for the family of polynomial-size circuits \(\mathcal{D}_\lambda \) defined in (5) below. We construct an offline witness encryption scheme
an SSS-NIZK scheme for \( L_\mathsf{{enc}}\) (Definition 4), and \(i\mathcal O\) an indistinguishability obfuscator for the family of polynomial-size circuits \(\mathcal{D}_\lambda \) defined in (5) below. We construct an offline witness encryption scheme  for \(L \in \mathsf{NP} \) that can be decided by a (circuit) witness relation \(R:\{0,1\}^{\ell _x} \times \{0,1\}^{\ell _w} \rightarrow \{0,1\}\) as follows:
for \(L \in \mathsf{NP} \) that can be decided by a (circuit) witness relation \(R:\{0,1\}^{\ell _x} \times \{0,1\}^{\ell _w} \rightarrow \{0,1\}\) as follows:
-
 On input a security parameter
On input a security parameter  , do the following:
, do the following:-
– \((\textit{sk}_1,\textit{pk}_1) \leftarrow \mathsf{PK.Gen }(1^\lambda )\) and \((\textit{sk}_2,\textit{pk}_2) \leftarrow \mathsf{PK.Gen }(1^\lambda )\).
-
– \(\textit{crs}\leftarrow \mathsf{NIZK.G }(1^\lambda )\).
-
– Construct the circuit
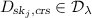 with \(j=1\)
with \(j=1\)
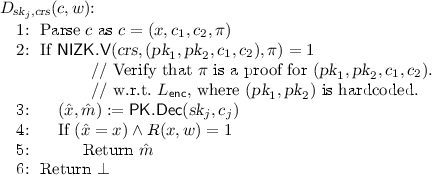 (5)
(5) -
–
 after padding
after padding  appropriately.Footnote 2
appropriately.Footnote 2
-
– Set
 and
and 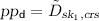 .
. -
– Output
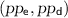 .
.
-
-
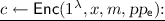 On input a security parameter
On input a security parameter 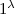 , a string \(x\in \{0,1\}^{\ell _x}\), a message \(m \in \mathcal{M}\), and
, a string \(x\in \{0,1\}^{\ell _x}\), a message \(m \in \mathcal{M}\), and 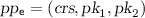 , Enc does the following:
, Enc does the following:-
–
 .
. -
– \(c_1 := \mathsf{PK.Enc }(\textit{pk}_1,(x,m); r_1)\) and \(c_2 := \mathsf{PK.Enc }(\textit{pk}_2,(x,m); r_2)\).
-
– \(\pi \leftarrow \mathsf{NIZK.P }\big (\textit{crs}, (\textit{pk}_1,\textit{pk}_2, c_1,c_2), (x,m,r_1 ,r_2)\big )\).
-
– Output \(c:=(x,c_1, c_2, \pi )\).
-
-
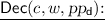 On input a ciphertext \(c=(x,c_1, c_2, \pi )\), a string \(w\in \{0,1\}^{\ell _w}\) and parameters
On input a ciphertext \(c=(x,c_1, c_2, \pi )\), a string \(w\in \{0,1\}^{\ell _w}\) and parameters 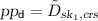 , Dec interprets \(\tilde{D}_{\textit{sk}_1,\textit{crs}}\) as a circuit and outputs \(m:=\tilde{D}_{\textit{sk}_1,\textit{crs}}(c,w)\).
, Dec interprets \(\tilde{D}_{\textit{sk}_1,\textit{crs}}\) as a circuit and outputs \(m:=\tilde{D}_{\textit{sk}_1,\textit{crs}}(c,w)\).
Theorem 1
\(\mathsf{OWE}\!=\!(\mathsf{Setup }, \mathsf{Enc }, \mathsf{Dec })\) in Construction 1 is a selectively-secure offline witness encryption scheme if \(\mathsf{PKE }\) is a CPA-secure PKE scheme, \(\mathsf{{NIZK}}\) an SSS-NIZK scheme, and \(i\mathcal O\) an indistinguishability obfuscator for \(\mathcal{D}_\lambda \).
Proof. Assume towards contradiction that there exists a non-uniform PPT adversary \(\mathcal{A}\) that distinguishes  from
from  with non-negligible probability. We reach a contradiction by first constructing a series of games \(\mathbf {Exp}^{(i)}\) defined in Fig. 4, where by construction,
with non-negligible probability. We reach a contradiction by first constructing a series of games \(\mathbf {Exp}^{(i)}\) defined in Fig. 4, where by construction,  and
and  , and then proving for \(i=0,1,\ldots , 5\) that \(\mathbf {Exp}^{(i)}\) and \(\mathbf {Exp}^{(i+1)}\) are computationally indistinguishable.
, and then proving for \(i=0,1,\ldots , 5\) that \(\mathbf {Exp}^{(i)}\) and \(\mathbf {Exp}^{(i+1)}\) are computationally indistinguishable.
Hybrid games used in the proof of Theorem 1
\(\mathbf {Exp}^{(1)}\) differs from \(\mathbf {Exp}^{(0)}\) in that the CRS \(\textit{crs}\) for the NIZK and the proof \(\pi \) are simulated rather than honestly generated. The zero-knowledge property of \(\mathsf{{NIZK}}\) guarantees that honestly generated CRSs and proofs are indistinguishable from simulated ones by PPT adversaries.
Proposition 1
\(\mathbf {Exp}^{(0)}(\lambda )\) and \(\mathbf {Exp}^{(1)}(\lambda )\) are computationally indistinguishable if \(\mathsf{{NIZK}}\) is zero-knowledge.
\(\mathbf {Exp}^{(2)}\) differs from \(\mathbf {Exp}^{(1)}\) in that the second ciphertext \(c_2\) is generated as \(\mathsf{PK.Enc }(\textit{pk}_2,(x,\underline{m_1}))\) rather than \(\mathsf{PK.Enc }(\textit{pk}_2,(x,m_0))\). (\(D_{\textit{sk}_1,\textit{crs}}\) and (\(\pi ,\textit{crs})\) are the same as in \(\mathbf {Exp}^{(1)}\).) The CPA-security of \(\mathsf{PKE }\) for key \(\textit{pk}_2\) guarantees that this change is indistinguishable by PPT adversaries.
Proposition 2
\(\mathbf {Exp}^{(1)}(\lambda )\) and \(\mathbf {Exp}^{(2)}(\lambda )\) are computationally indistinguishable if \(\mathsf{PKE }\) is CPA-secure.
\(\mathbf {Exp}^{(3)}\) differs from \(\mathbf {Exp}^{(2)}\) in that the circuit \(D_{\underline{\textit{sk}_2},\textit{crs}}\) is obfuscated instead of \(D_{\textit{sk}_1,\textit{crs}}\). Statistical simulation-soundness of \(\mathsf{{NIZK}}\) now guarantees that \(D_{\textit{sk}_1,\textit{crs}}\) and \(D_{\textit{sk}_2,\textit{crs}}\) are functionally equivalent when \(\textit{crs}\) is simulated for the statement \(y:=(\textit{pk}_1,\textit{pk}_2,c_1,c_2)\). It then follows from the security of \(i\mathcal O\) that their obfuscations are computationally indistinguishable.
Proposition 3
\(\mathbf {Exp}^{(2)}(\lambda )\) and \(\mathbf {Exp}^{(3)}(\lambda )\) are computationally indistinguishable if \(\mathsf{{NIZK}}\) is statistically simulation-sound, and \(i\mathcal O\) is secure.
\(\mathbf {Exp}^{(4)}\) differs from \(\mathbf {Exp}^{(3)}\) in that the first ciphertext \(c_1\) is generated as \(\mathsf{PK.Enc }(\textit{pk}_1,(x,\underline{m_1}))\) rather than \(\mathsf{PK.Enc }(\textit{pk}_1,(x,m_0))\). (\(D_{\textit{sk}_2,\textit{crs}}\) and (\(\pi ,\textit{crs})\) are the same as in \(\mathbf {Exp}^{(3)}\).) Now CPA security of \(\mathsf{PKE }\) w.r.t. \(\textit{pk}_1\) implies that this change is computationally indistinguishable.
Proposition 4
\(\mathbf {Exp}^{(3)}(\lambda )\) and \(\mathbf {Exp}^{(4)}(\lambda )\) are computationally indistinguishable if \(\mathsf{PKE }\) is CPA-secure.
\(\mathbf {Exp}^{(5)}\) differs from \(\mathbf {Exp}^{(4)}\) in that \(D_{\underline{\textit{sk}_1},\textit{crs}}\) is obfuscated rather than \(D_{\textit{sk}_2,\textit{crs}}\). Statistical simulation soundness of \(\mathsf{{NIZK}}\) together with security of \(i\mathcal O\) implies that this change is computationally indistinguishable.
Proposition 5
\(\mathbf {Exp}^{(4)}(\lambda )\) and \(\mathbf {Exp}^{(5)}(\lambda )\) are computationally indistinguishable if \(\mathsf{{NIZK}}\) is statistically simulation-sound, and \(i\mathcal O\) is secure.
\(\mathbf {Exp}^{(6)}\) is the original game  , and differs from \(\mathbf {Exp}^{(5)}\) in that the CRS and NIZK proof \((\textit{crs}, \pi )\) are honestly generated rather than simulated. By zero-knowledge of \(\mathsf{{NIZK}}\) this change is computationally indistinguishable.
, and differs from \(\mathbf {Exp}^{(5)}\) in that the CRS and NIZK proof \((\textit{crs}, \pi )\) are honestly generated rather than simulated. By zero-knowledge of \(\mathsf{{NIZK}}\) this change is computationally indistinguishable.
Proposition 6
\(\mathbf {Exp}^{(5)}(\lambda )\) and \(\mathbf {Exp}^{(6)}(\lambda )\) are computationally indistinguishable if \(\mathsf{{NIZK}}\) is zero-knowledge.
Theorem 1 follows from Propositions 1–6. We formally prove Theorem 1 in the full version [AFP15]. \(\square \)
4 Offline Functional Witness Encryption
Boyle et al. [BCP14] consider both extractable and indistinguishability-based notions of FWE. We consider an offline version of their indistinguishability-based notion. Here the encryption algorithm takes input an instance x and a pair (m, f) of a message and a description of a circuit f and outputs a ciphertext c. A party knowing a witness w for x now does not learn m itself, but only the function f(m, w). Security requires computational indistinguishability of encryptions of \((x,(m_0,f_0))\) and \((x,(m_1,f_1))\) as long as \(f_0(m_0,w)=f_1(m_1,w)\) for all w with \(R(x,w)=1\).
Definition 6
(Offline FWE). \(\mathsf{OWE}=(\mathsf{Setup }, \mathsf{Enc }, \mathsf{Dec })\) from Definition 5 is an offline FWE scheme if the following hold:
-
Correctness: For all \(\lambda \in \mathbb {N}\),
 such that \(R(x,w)=1\), \(m\in \mathcal{M}\):
such that \(R(x,w)=1\), \(m\in \mathcal{M}\): 
-
Security: \(\mathsf{OWE}\) is selectively secure if for every non-uniform PPT adversary
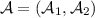 in
in 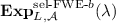 (Fig. 5) we have
(Fig. 5) we have 
Construction 2
(Offline functional WE). This construction is defined exactly as Construction 1, except that in the definition of the decryption circuit in Eq. (5) on page we replace
with
Theorem 2
Construction 2 is a selectively-secure offline functional witness encryption scheme under the same assumptions as in Theorem 1.
The proof is analogous to the proof of Theorem 1.Footnote 3
5 Instantiating Enc
We now show how to efficiently instantiate the encryption algorithm of both our offline-WE schemes over a bilinear group and prove its security under a standard assumption (SXDH) and without recurring to random oracles. We use ElGamal encryption [ElG84] for the public-key encryption scheme and build an SSS-NIZK proof system from Groth-Sahai proofs [GS08] following the abstract blueprint for it given in [GGH+13b].
5.1 Tools
Bilinear Groups. \(\mathcal G\) is a bilinear-group generator if given a security parameter \(1^\lambda \) it returns the description of a bilinear group \(\varLambda =(p,\mathbb {G},\mathbb {H},\mathbb {T},e,g,h)\) where:
-
\(\mathbb {G}\), \(\mathbb {H}\) and \(\mathbb {T}\) are groups of prime order p, where p is of bit-length \(\lambda \);
-
\(e:\mathbb {G}\times \mathbb {H}\rightarrow \mathbb {T}\) is a bilinear map, that is, \(e(R^a,S^b) = e(R,S)^{ab}\) for all \(R\in \mathbb {G}\), \(S\in \mathbb {H}\), \(a,b\in \mathbb {Z}_p\);
-
g and h generate \(\mathbb {G}\) and \(\mathbb {H}\), resp., and e(g, h) generates \(\mathbb {T}\).
We use Type-3 bilinear groups [GPS08], in which no efficiently computable homomorphisms are assumed to exist between \(\mathbb {G}\) and \(\mathbb {H}\). We can therefore assume that the decisional Diffie-Hellman assumption (DDH) holds in \(\mathbb {G}\), that is
for any non-uniform PPT \(\mathcal{A}\). We moreover assume DDH holds in \(\mathbb {H}\), that is, the same holds with g replaced by h above. The SXDH assumption for a bilinear-group generator \(\mathcal G\) is that DDH holds in both \(\mathbb {G}\) and \(\mathbb {H}\).
ElGamal Encryption. We use ElGamal encryption to encrypt message vectors in \(\mathbb {G}^\ell \), for some fixed \(\ell \). A secret key \({\varvec{x}}\leftarrow \mathbb {Z}_p^{\,\ell }\) defines a public key \({\varvec{X}}\in \mathbb {G}^\ell \) via \(X_i:=g^{x_i}\) for \(i=1, \ldots , \ell \). A message \({\varvec{M}} = (M_i)_{i=1}^\ell \in \mathbb {G}^\ell \) is encrypted under \({\varvec{X}}\) by choosing \(r\leftarrow \mathbb {Z}_p^*\) and setting
Note that by using the same randomness for every component, we decrease ciphertext length. CPA security follows from the DDH assumption in \(\mathbb {G}\) via a standard hybrid argument.
Groth-Sahai Proofs. Groth-Sahai (GS) proofs [GS08] are efficient non-interactive witness-indistinguishableFootnote 4 (WI) proofs for several types of equations in bilinear groups. We only require linear pairing-product equations over variables \(W_1,\ldots ,W_n\in \mathbb {H}\), which are of the form
defined by \((A_i)_{i=1}^n \in \mathbb {G}^n\), and \(t\in \mathbb {T}\). (As a convention, we always underline the variables.) GS proofs allow a prover to prove that there exists an assignment to the variables that satisfies a given set of equations. Groth-Sahai proofs are perfectly sound (meaning there do not exist proofs for an unsatisfiable set of equations). The instantiation of GS proofs we use is WI under the SXDH assumption. The cost of a proof is 2 elements from \(\mathbb {H}\) per variable and 2 elements from \(\mathbb {G}\) per equation.
5.2 Instantiation
Using ElGamal encryption, we encode pairs \(M=(x,m)\) (that is, statement/message pairs which we encrypt in our offline-WE instantiation) as a vector of group elements from \(\mathbb {G}^\ell \). We thus assume that there exists an efficiently decodable encoding \(\textsf {Cd}\) of pairs (x, m) into \(\mathbb {G}^\ell \) [FJT13].
We now construct an SSS-NIZK proof system which allows us to prove that 2 ElGamal ciphertexts under different keys encrypt the same message M. We assume that the ciphertexts are always different from \((1,\ldots ,1)\), which for honestly generated ciphertext is the case as \(c_{l+1}\ne 1\) in (6).
A CRS for this system consists of a CRS for GS proofs together with a commitment C to \(\mathbf{1}\). An SSS-NIZK proof for the statement y: “\({\varvec{c}}^{(1)}\) and \({\varvec{c}}^{(2)}\) encrypt the same message” is a GS proof for the statement

Statistical soundness follows from perfect soundness of GS proofs: since C is not a commitment to \(({\varvec{c}}^{(1)},{\varvec{c}}^{(2)})\ne \mathbf{1}\), the first clause in (8) must hold. Zero-knowledge holds since given a statement \(y=({\varvec{c}}^{(1)},{\varvec{c}}^{(2)})\) the simulator can set the value C in the CRS to a commitment to y; a proof for y can then be simulated by using use the second clause in (8). Since this is (in an information-theoretic sense) the only statement that can be simulated, statistical simulation-soundness (SSS) holds as well. We now present the details.
Language. A statement for our language \( L_\mathsf{{enc}}\) defined in Eq. (4) is of the form \(({\varvec{X}}^{(1)},{\varvec{X}}^{(2)},{\varvec{c}}^{(1)},{\varvec{c}}^{(2)})\), where \({\varvec{X}}^{(1)},{\varvec{X}}^{(2)}\in \mathbb {G}^\ell \) are ElGamal encryption keys and \({\varvec{c}}^{(1)},{\varvec{c}}^{(2)}\in \mathbb {G}^{\ell +1}\) are ElGamal encryptions of the same message. Since the public keys are hard-coded in the description of \(D_{\textit{sk}_j,\textit{crs}}(c,w)\) (defined in (5)), we need not include them in the statement. We therefore construct a proof system for the language
where M is an encoding of \((x,m)\).
Commitment. We define a non-interactive commitment scheme that lets us commit to a message \(\big ({\varvec{c}}^{(1)},{\varvec{c}}^{(2)}\big )\in \mathbb {G}^{2\ell +2}\) as follows:
-
The commitment key is \(\textit{ck}=\big (K^{(1)}_1,\ldots ,K^{(1)}_{\ell +1},K^{(2)}_1,\ldots ,K^{(2)}_{\ell +1}\big )\leftarrow \mathbb {G}^{2\ell +2}\).
-
A commitment \(\textsf {Com}\big (\textit{ck},({\varvec{c}}^{(1)},{\varvec{c}}^{(2)})\big )\) to a message \(\big ({\varvec{c}}^{(1)},{\varvec{c}}^{(2)}\big )\in \mathbb {G}^{2\ell +2}\) is computed by picking \(r_c\leftarrow \mathbb {Z}_p\) and setting
$${\varvec{C}}=\Big (\big (C^{(i)}_j:=c^{(i)}_j\cdot (K^{(i)}_j)^{r_c}\big )^{i=1,2}_{j=1\ldots \ell +1},\,C':=g^{r_c}\Big ).$$
A commitment can be opened by publishing the “opening” \(W= h^{r_c}\), which allows verifying that \({\varvec{C}}\) is a commitment to \(({\varvec{c}}^{(1)},{\varvec{c}}^{(2)})\) by checking
This yields a perfectly binding commitment scheme for messages from \(\mathbb {G}^{2\ell +2}\), and, as the commitment is an ElGamal encryption, it is computationally hiding under the DDH assumption in \(\mathbb {G}\).
Using \(\textsf {Com}\) we now define our SSS proof system for showing that two ciphertexts as in (6) encrypt the same message \({\varvec{M}}\).
CRS Generation. A CRS is generated by computing a CRS for GS proofs \(\textit{crs}_\text {GS}\leftarrow \textsf {GS}.\textsf {G}(\varLambda )\), picking a commitment key \(\textit{ck}\leftarrow \mathbb {G}^{2\ell +2}\) computing \({\varvec{C}}\leftarrow \textsf {Com}(\textit{ck},(1,\ldots ,1))\) and outputting \( \textit{crs}:= (\textit{crs}_\text {GS},\textit{ck},{\varvec{C}}) \).
Proof. We show how to prove, under CRS \((\textit{crs}_\text {GS},({\varvec{K}}^{(1)},{\varvec{K}}^{(2)}),{\varvec{C}})\), a statement \(({\varvec{c}}^{(1)},{\varvec{c}}^{(2)})\in L_{{\varvec{X}}^{(1)},{\varvec{X}}^{(2)}}\), using as witness \((r_1,r_2)\) such that \({\varvec{c}}^{(i)} = \big ((M_j\cdot (X_j^{(i)})^{r_i})_{j=1}^\ell ,g^{r_i}\big )\) for some \({\varvec{M}}\in \mathbb {G}^\ell \). Consider the following set of linear pairing-product equations in variables \(H_c,H_e,W_1,W_2,W_c\in \mathbb {H}\):
A proof of our SSS-NIZK proof system is a (witness-indistinguishable) GS proof of satisfiability of the above equation system and is computed by using witness \((r_1,r_2)\) and setting the variables to
Verification. A proof \(\pi \) for statement \(({\varvec{c}}^{(1)},{\varvec{c}}^{(2)})\) under CRS \((\textit{crs}_\text {GS},\textit{ck},{\varvec{C}})\) is verified by verifying the GS proof \(\pi \) under \(\textit{crs}_\text {GS}\) of satisfiability of equations (9)–(13) defined by the values in \({\varvec{c}}^{(1)},{\varvec{c}}^{(2)},\textit{ck}=({\varvec{K}}^{(1)},{\varvec{K}}^{(2)})\) and \({\varvec{C}} = ((C^{(i)}_j)^{i=1,2}_{j=1\ldots \ell +1},C':=g^{r_c})\).
Completeness of our SSS NIZK proof system follows from completeness of GS proofs together with the fact that the values in (14) satisfy (9)–(13).
Soundness. Below we show that a proof of satisfiability of Eqs. (9)–(13) proves that

Since GS proofs are perfectly sound and an honestly generated CRS contains a commitment to \((1,\ldots ,1)\), which is a valid statement, a valid proof shows that the “either” clause above is satisfied, thus \(({\varvec{c}}^{(1)},{\varvec{c}}^{(2)})\in L_{\textit{pk}_1,\textit{pk}_2}\). We now show (15).
-
Equation (9) proves that either \(H_c\ne 1\) or \(H_e\ne 1\); since \(e(g,1)\,e(g,1)\ne e(g,h)\).
-
If \(H_c\ne 1\) then (10)–(11) prove that \((C^{(1)}_1,\ldots ,C^{(1)}_{\ell +1},C^{(2)}_{1}, \ldots ,C^{(2)}_{\ell +1},C')\) commits to \((c^{(1)}_1,\ldots ,c^{(1)}_{\ell +1},c^{(2)}_{1}\ldots ,c^{(2)}_{\ell +1})\):
Let \(\eta ,\omega \in \mathbb {Z}_p\), \(\eta \ne 0\) (since \(H_c\ne 1\)), be such that \(H_c=h^\eta \) and \(W_c=h^\omega \). From (11) we have \(C'=g^{\omega /\eta }\), whereas the equations in (10) yield \(C^{(i)}_j\cdot (c^{(i)}_j)^{-1} = (K^{(i)}_j)^{\omega /\eta }\), thus \(C^{(i)}_j = c^{(i)}_j\cdot (K^{(i)}_j)^{\omega /\eta }\), which together means that \((C^{(1)}_1,\ldots ,C^{(2)}_{\ell +1},C')\) is a commitment to \((c^{(1)}_1,\ldots ,c^{(2)}_{\ell +1})\) with randomness \(r_c=\omega /\eta \).
-
If \(H_e\ne 1\) then with \(\eta \ne 0,\omega _1\) and \(\omega _2\) such that \(H_e=h^\eta \) and \(W_i=h^{\omega _i}\) the equations in (13) yield that \(c^{(i)}_{\ell +1}=g^{\omega _i/\eta }\), for \(i=1,2\). Set \(r_i:={\omega _i/\eta }\) and let \(m^{(i)}_j\) be (the unique values) such that \(c^{(i)}_j=g^{m^{(i)}_j}\cdot (X^{(i)}_j)^{r_i}\). Then the equations in (12) yield \(c^{(1)}_j\!\cdot \! (c^{(2)}_j)^{-1} = (X^{(1)}_j)^{r_1}\cdot (X^{(2)}_j)^{-r_2}\), thus \(g^{m^{(1)}_j} = g^{m^{(2)}_j}\) for all \(j=1,\ldots ,\ell \), meaning \({\varvec{c}}^{(1)}\) and \({\varvec{c}}^{(2)}\) encrypt the same message.
Simulation. Given a statement \(({\varvec{c}}^{(1)},{\varvec{c}}^{(2)})\), the simulator sets up the CRS by choosing \(r_c\leftarrow \mathbb {Z}_p\) and setting \({\varvec{C}}:=\textsf {Com}(\textit{ck},({\varvec{c}}^{(1)},{\varvec{c}}^{(2)});r_c)\). It simulates a proof for statement \(({\varvec{c}}^{(1)},{\varvec{c}}^{(2)})\in L_{\textit{pk}_1,\textit{pk}_2}\) by computing a GS proof for Eqs. (9)–(13) by instantiating the variables as
Since the commitment in the CRS is hiding under DDH in \(\mathbb {G}\), and since GS proofs are witness-indistinguishable under SXDH, this simulation is also indistinguishable under SXDH (which implies DDH in \(\mathbb {G}\)). Statistical simulation-soundness holds, since once the CRS is set up, \(({\varvec{c}}^{(1)},{\varvec{c}}^{(2)})\) is the only statement for which a proof using the 2\(^\text {nd}\) clause in (15) can be computed. Any other proof must use the first clause, meaning the statement must be in the language.
5.3 Cost of an Encryption
In standard implementations of bilinear groups for 128-bit security, \(\mathbb {G}\) elements are of size 256 bits and \(\mathbb {H}\) elements are of size 512 bits. Let \(\ell \) be such that pairs (x, m) are of size \(< 128\cdot \ell \) bits, that is, they can be mapped to \(\mathbb {G}^\ell \).
An encryption in our WE scheme then consists of two ElGamal ciphertexts (each in \(\mathbb {G}^{\ell +1}\)) and a GS proof with 5 variables in \(\mathbb {H}\) (requiring 10 elements from \(\mathbb {H}\)) and \(3\ell +6\) linear equations (requiring \(6\ell +12\) elements from \(\mathbb {G}\)). Computing an ElGamal encryption requires \(\ell +1\) exponentiations and \(\ell \) group operations in \(\mathbb {G}\). The 2 elements from \(\mathbb {H}\) required for each variable require 2 exponentiations and one group operation in \(\mathbb {H}\). The 2 elements from \(\mathbb {G}\) required for each equation are computed using together 4 exponentiations and 2 group operations in \(\mathbb {G}\).
With the above instantiation the output of \(\mathsf{Enc }\) is in \(\mathbb {G}^{8\ell +14}\times \mathbb {H}^{10}\). If two group elements suffice to encode pairs (x, m) then one encryption has \(\approx 1.6\) kB. For every 128-bit increase of the message length, the encryption only grows by 8 elements from \(\mathbb {G}\), that is 0.25 kB.
Notes
- 1.
Such a key consists of a pair
 of a salt and a hashed password
of a salt and a hashed password  for a password-hashing function \(\textsf {PH}\). Given a WE for the NP-language
for a password-hashing function \(\textsf {PH}\). Given a WE for the NP-language  , messages are encrypted w.r.t. statements
, messages are encrypted w.r.t. statements 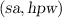 and can be decrypted using witness
and can be decrypted using witness 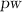 such that
such that  .
. - 2.
W.l.o.g. we assume that \(|D_{\textit{sk}_1,\textit{crs}}|=|D_{\textit{sk}_2,\textit{crs}}|\); otherwise we always pad to the maximum possible length.
- 3.
The only change to be made is in the proof of Proposition 3, which is the only time we use the fact that \(\bar{x}\notin L\). In the description of \(\mathcal {B}\), \(\bar{m}_j\) is replaced by \((\bar{m}'_j,\bar{f}_j)\) for \(j=0,1\). For Case 1 we now argue that \(D_1((\bar{x},\bar{c}_1,\bar{c}_2,\pi ),w)=D_2((\bar{x},\bar{c}_1,\bar{c}_2,\pi ),w)\) for all \(\pi ,w\) as follows: If \(R(\bar{x},w)=0\) then both circuits output \(\bot \). If \(R(\bar{x},w)=1\) then by the winning condition for the security game we have
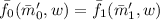 for all w. Since \(\bar{c}_1\) decrypts to \((\bar{x},(\bar{m}'_0,\bar{f}_0))\) and \(\bar{c}_2\) decrypts to \((\bar{x},(\bar{m}'_1,\bar{f}_1))\), both circuits return \(\bar{f}_0(\bar{m}'_0,w)\).
for all w. Since \(\bar{c}_1\) decrypts to \((\bar{x},(\bar{m}'_0,\bar{f}_0))\) and \(\bar{c}_2\) decrypts to \((\bar{x},(\bar{m}'_1,\bar{f}_1))\), both circuits return \(\bar{f}_0(\bar{m}'_0,w)\). - 4.
Witness-indistinguishability for a proof system for a language L means the following: no PPT adversary that given \(\textit{crs}\) chooses \(y,w_0,w_1\) with \(R(y,w_0)=R(y,w_1)=1\) can distinguish \(\pi _0\leftarrow \mathsf{P }(\textit{crs}, y, w_0)\) from \(\pi _1\leftarrow \mathsf{P }(\textit{crs}, y, w_1)\).
References
Ananth, P., Boneh, D., Garg, S., Sahai, A., Zhandry, M.: Differing-inputs obfuscation and applications. IACR Cryptology ePrint Archive, 2013:689 (2013)
Abusalah, H., Fuchsbauer, G., Pietrzak, K.: Offline Witness Encryption. Cryptology ePrint Archive, Report 2015/838 (2015). http://eprint.iacr.org/
Apon, D., Huang, Y., Katz, J., Malozemoff, A.J.: Implementing cryptographic program obfuscation. Cryptology ePrint Archive, Report 2014/779 (2014). http://eprint.iacr.org/
Boyle, E., Chung, K.-M., Pass, R.: On extractability obfuscation. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 52–73. Springer, Heidelberg (2014)
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S.P., Yang, K.: On the (im)possibility of obfuscating programs. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 1–18. Springer, Heidelberg (2001)
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S., Yang, K.: On the (im)possibility of obfuscating programs. J. ACM 59(2), 1–48 (2012)
Bellare, M., Hoang, V.T.: Adaptive witness encryption and asymmetric password-based cryptography. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 308–331. Springer, Heidelberg (2015)
Even, S., Goldreich, O., Micali, S.: On-line/off-line digital signatures. J. Cryptol. 9(1), 35–67 (1996)
El Gamal, T.: A public key cryptosystem and a signature scheme based on discrete logarithms. In: Blakely, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 10–18. Springer, Heidelberg (1985)
Fouque, P.-A., Joux, A., Tibouchi, M.: Injective encodings to elliptic curves. In: Boyd, C., Simpson, L. (eds.) ACISP. LNCS, vol. 7959, pp. 203–218. Springer, Heidelberg (2013)
Garg, S., Gentry, C., Halevi, S.: Candidate multilinear maps from ideal lattices. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 1–17. Springer, Heidelberg (2013)
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: 54th FOCS, pp. 40–49. IEEE Computer Society Press, October 2013
Garg, S., Gentry, C., Halevi, S., Wichs, D.: On the implausibility of differing-inputs obfuscation and extractable witness encryption with auxiliary input. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 518–535. Springer, Heidelberg (2014)
Garg, S., Gentry, C., Sahai, A., Waters, B.: Witness encryption and its applications. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 467–476. ACM Press, June 2013
Gentry, C., Lewko, A., Waters, B.: Witness encryption from instance independent assumptions. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 426–443. Springer, Heidelberg (2014)
Galbraith, S.D., Paterson, K.G., Smart, N.P.: Pairings for cryptographers. Discrete Appl. Math. 156(16), 3113–3121 (2008)
Groth, J., Sahai, A.: Efficient non-interactive proof systems for bilinear groups. In: Smart, N.P. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 415–432. Springer, Heidelberg (2008)
Naor, M., Yung, M.: Public-key cryptosystems provably secure against chosen ciphertext attacks. In: 22nd ACM STOC, pp. 427–437. ACM Press, May 1990
Sahai, A.: Non-malleable non-interactive zero knowledge and adaptive chosen-ciphertext security. In: 40th FOCS, pp. 543–553. IEEE Computer Society Press, October 1999
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005)
Zhandry, M.: How to avoid obfuscation using witness PRFs. Cryptology ePrint Archive, Report 2014/301 (2014). http://eprint.iacr.org/2014/301
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
Abusalah, H., Fuchsbauer, G., Pietrzak, K. (2016). Offline Witness Encryption. In: Manulis, M., Sadeghi, AR., Schneider, S. (eds) Applied Cryptography and Network Security. ACNS 2016. Lecture Notes in Computer Science(), vol 9696. Springer, Cham. https://doi.org/10.1007/978-3-319-39555-5_16
Download citation
DOI: https://doi.org/10.1007/978-3-319-39555-5_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-39554-8
Online ISBN: 978-3-319-39555-5
eBook Packages: Computer ScienceComputer Science (R0)




 in
in  (Fig.
(Fig. 
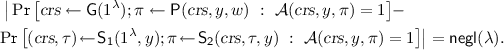
 : On input a security parameter
: On input a security parameter  and parameters for decryption
and parameters for decryption  .
. : On input a security parameter
: On input a security parameter  ,
,  : On input a ciphertext c, a string
: On input a ciphertext c, a string  and decryption parameters
and decryption parameters  ,
,  .
. such that
such that 
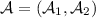 in
in  (Fig.
(Fig. 
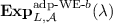 (Fig.
(Fig. 

 On input a security parameter
On input a security parameter  , do the following:
, do the following: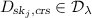 with
with 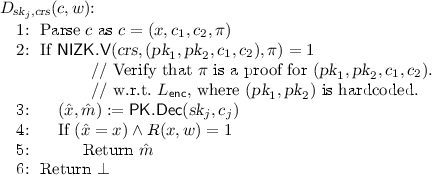
 after padding
after padding  appropriately.
appropriately. and
and 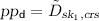 .
.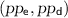 .
.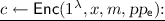 On input a security parameter
On input a security parameter 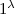 , a string
, a string 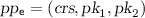 ,
,  .
.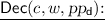 On input a ciphertext
On input a ciphertext 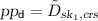 ,
, 
 such that
such that 
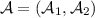 in
in 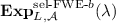 (Fig.
(Fig. 

 of a salt and a hashed password
of a salt and a hashed password  for a password-hashing function
for a password-hashing function  , messages are encrypted w.r.t. statements
, messages are encrypted w.r.t. statements 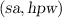 and can be decrypted using witness
and can be decrypted using witness 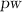 such that
such that  .
.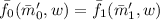 for all w. Since
for all w. Since