Abstract
We study interacting components and their compatibility with respect to synchronous and asynchronous composition. The behavior of components is formalized by I/O-transition systems. Synchronous composition is based on simultaneous execution of shared output and input actions of two components while asynchronous composition uses unbounded FIFO-buffers for message transfer. In both contexts we study compatibility notions based on the idea that any output issued by one component should be accepted as an input by the other. We distinguish between strong and weak versions of compatibility, the latter allowing the execution of internal actions before a message is accepted. We consider open systems and study conditions under which (strong/weak) synchronous compatibility is sufficient and necessary to get (strong/weak) asynchronous compatibility. We show that these conditions characterize half-duplex systems. Then we focus on the verification of weak asynchronous compatibility for possibly non half-duplex systems and provide a decidable criterion that ensures weak asynchronous compatibility.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Half-duplex System
- Asynchronous Composition
- Compatibility Notion
- Unbounded FIFO Buffers
- Synchronous Composition
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Structuring software systems by interconnected components is a standard technique in software engineering. In this work we consider active components with a well defined behavior which work together by message exchange. Each single component has a life cycle during which it sends and receives messages and it can also perform internal actions in between. For the correct functioning of the overall system it is essential that no communication errors occur during component interactions. There are different types of communication errors which are influenced by the communication style and system architecture. In our study we focus on bidirectional, peer to peer communication and we discuss synchronous and asynchronous message exchange. The former is based on a rendezvous mechanism such that two components must execute shared output and input actions together. The latter uses unbounded FIFO-buffers which hold the messages sent by one component and received by the other. In this context two prominent types of communication errors can be distinguished. The first one concerns situations, in which an output of one component is not accepted as an input by the other, the second one occurs if a component waits for an input which is never delivered. Inspired by the work of de Alfaro and Henzinger [11] on compatibility of interface automata, we focus on the former kind of communication error which itself gives rise to several variations.
De Alfaro and Henzinger deal with open systems and synchronous communication. They consider two interface automata to be compatible if there exists a “helpful” environment such that the interacting components can never reach an error state where “one of the automata may produce an output action that is in the input alphabet of the other automaton, but is not accepted”. We allow open systems as well but follow the “pessimistic” approach where components should be compatible in any environment. For the formalization of component behaviors we use I/O-transition systems (IOTSes) and call two IOTses strongly synchronously compatible if the compatibility requirement from above holds. In many practical examples it turns out that before interacting with the sending component the receiving component should still be able to perform some internal actions in between. This leads to our notion of weak synchronous compatibility (which works well with weak bisimulation and refinement [4]).
In this work we study also asynchronous compatibility of components communicating via unbounded message queues. Asynchronous compatibility requires that whenever a message queue is not empty, the receiver component must be able to take the next element of the queue; a property called specified reception in [6]. We distinguish again between strong and weak versions of asynchronous compatibility. In the asynchronous context the weak compatibility notion is particularly powerful since it allows a component, before it inputs a message waiting in the queue, still to put itself messages in its output queue (since we consider such enqueue actions as internal). We have shown in [3] that also weak asynchronous compatibility works well with weak bisimulation and refinement.
An obvious question is to what extent synchronous and asynchronous compatibility notions can be related to each other and, if this is not possible, which proof techniques can be used to verify asynchronous compatibility. We contribute to this issues with the following results:
-
1.
We establish a relationship between strong/weak synchronous and asynchronous compatibility of two components (Sects. 4.1 and 4.2) and formulate three equivalent (and decidable) conditions such that strong/weak synchronous compatibility is sufficient, and even necessary, for strong/weak asynchronous compatibility. One of the three conditions is the half-duplex property: at any time at most one message queue is not empty; see, e.g., [5, 9].
-
2.
In the second part of this work (Sect. 5), we consider general, possibly non half-duplex systems, and study the verification of weak asynchronous compatibility in such cases. Due to the unboundedness of the FIFO-buffers the problem is not decidable [6]. We investigate, however, decidable and powerful criteria which allow us to prove weak asynchronous compatibility.
Related Work. In our study we focus on asynchronous message exchange via FIFO-buffers. Of course, other kinds of asynchronous communication using, e.g., event pools for modeling the composition of state machines in UML, or communication channels storing messages as bags are often considered. For instance, in [12], we have studied (modal) asynchronous I/O-transition systems and Petri nets where communication is realized by unbounded, but unordered, channel places. We have shown that in this case various compatibility problems are decidable. Systems of finite automata which contain both FIFO-buffers and bag channels are studied in [10] where topologies are investigated in which the reachability problem is decidable.
Compatibility notions are mostly considered for synchronous systems, since in this case compatibility checking is easier manageable and even decidable if the behaviors of local components have finitely many states. Some approaches use process algebras to study compatibility, like [7] using the \(\pi \)-calculus, others investigate interface theories with binary compatibility relations preserved by refinement, see, e.g., [14, 16] for modal interfaces, or consider n-ary compatibility in multi-component systems like, e.g., team automata in [8]. A prominent example of multi-component systems with asynchronous communication via unbounded FIFO-buffers are CFSMs [6], for which many problems, like unspecified reception, are undecidable. The situation is different, if half-duplex systems of two CFSMs are considered. Cécé and Finkel have shown in [9] that then the set of reachable configurations is recognizable and several problems, including unspecified reception, are decidable. The approach in [5] even suggests to built in the half-duplex property in the system semantics to facilitate desynchronization.
There is, however, not much work on relationships between synchronous and asynchronous compatibility. An exception are the approaches of Basu, Bultan, Ouederni, and Salaün; see [1, 2] for language-based and [15] for LTS-based semantics. Their crucial assumption is usually synchronizability which requires, for LTSes, a branching bisimulation between the synchronous and the asynchronous versions of a system (with message consumption from buffers considered internal). Under this hypothesis [15] proposes methods to prove compatibility of asynchronously communicating peers by checking synchronous compatibility. Their central notion is UR compatibility which is close to our weak compatibility concept but requires additionally deadlock-freeness. Obvious differences to our work are that [15] considers multi-component systems while we study binary compatibility relations. On the other hand, [15] considers closed systems while we allow open systems which can be incrementally extended to larger ones. Also our method for checking asynchronous compatibility is very different. In the first part of our work we rely on half-duplex systems (instead of synchronizability) and we show that for such systems synchronous and asynchronous compatibility are even equivalent. In the second part of our work we drop any assumptions and investigate powerful and decidable criteria for asynchronous compatibility of systems which are neither half-duplex nor synchronizable.
Quite close to the first part of our work is the study of half-duplex systems by Cécé and Finkel [9]. Due to their decidability result for unspecified reception (for two communicating CFSMs) it is not really surprising that we get an effective characterization of asynchronous compatibility and a way to decide it for components with finitely many states. A main difference to [9] is that we consider also synchronous systems and relate their compatibility properties to the asynchronous versions. Moreover, we deal with open systems as well and consider a weak variant of asynchronous compatibility, which we believe adds much power to the strong version. Finally, as explained above, a significant part of our work deals also with systems which are not necessarily half-duplex.
2 I/O-Transition Systems and Their Compositions
We start with the definitions of I/O-transition systems and their synchronous and asynchronous compositions which are the basis of the subsequent study.
Definition 1
(IOTS). An I/O-transition system is a quadruple \(A = ( states _A, start _A, act _A, {\mathop {\longrightarrow }\limits ^{}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}})\) consisting of a set of states \( states _A\), an initial state \( start _A \in states _A\), a set \( act _A = in _A \cup out _A \cup int _A\) of actions being the disjoint union of sets \( in _A\), \( out _A\) and \( int _A\) of input, output and internal actions resp., and a transition relation \({\mathop {\longrightarrow }\limits ^{}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} \subseteq states _A \times act_A \times states _A\).
We write \(s {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'\) instead of \((s,a,s') \in {\mathop {\longrightarrow }\limits ^{}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}}\). For \(X \subseteq act _A\) we write \(s {\xrightarrow {\,X\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{A}} s'\) if there exists a (possibly empty) sequence of transitions \(s {\mathop {\longrightarrow }\limits ^{a_1}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s_1 \ldots s_{n-1} {\mathop {\longrightarrow }\limits ^{a_n}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'\) involving only actions of X, i.e. \(a_1,\ldots ,a_n \in X\). A state \(s \in states _A\) is reachable if \( start _A {\xrightarrow {\, act _A\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{A}} s\). The set of reachable states of A is denoted by \(\mathcal {R}(A)\).
Two IOTSes A and B are (syntactically) composable if their actions only overlap on complementary types, i.e. \( act _A \cap act _B \subseteq (in_A \cap out_B) \cup (in_B \cap out_A)\). The set of shared actions \( act _A \cap act _B\) is denoted by \( shared (A,B)\). The synchronous composition of two IOTSes A and B is defined as the product of transition systems with synchronization on shared actions which become internal actions in the composition. Shared actions can only be executed together; they are blocked if the other component is not ready for communication. In contrast, internal actions and non-shared input and output actions can always be executed by a single component in the composition. These (non-shared) actions are called free actions in the following.
Definition 2
(Synchronous composition). Let A and B be two composable IOTSes. The synchronous composition of A and B is the IOTS \(A \otimes B = ( states _A \times states _B, ( start _A, start _B), act _{A \otimes B}, {\mathop {\longrightarrow }\limits ^{}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A \otimes B}}})\) where \( act _{A \otimes B}\) is the disjoint union of the input actions \( in _{A \otimes B} = ( in _A \cup in_B) \backslash shared (A,B)\), the output actions \( out _{A \otimes B} = ( out _A \cup out_B) \backslash shared (A,B)\), and the internal actions \( int _{A \otimes B} = int _A \cup int _B \cup shared (A,B)\). The transition relation of \(A \otimes B\) is the smallest relation such that
-
for all \(a \in act _A\backslash shared (A,B)\), if \(s {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'\), then \((s,t) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A \otimes B}}} (s',t)\) for all \(t \in states _B\),
-
for all \(a \in act _B\backslash shared (A,B)\), if \(t {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} t'\), then \((s,t) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A \otimes B}}} (s,t')\) for all \(s \in states _A\), and
-
for all \(a \in shared (A,B)\), if \(s {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'\) and \(t {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} t'\), then \((s,t) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A \otimes B}}} (s',t')\).
The synchronous composition of two IOTSes A and B yields a closed system if it has no input and output actions, i.e. \(( in _A \cup in_B) \backslash shared (A,B) = \emptyset \) and \(( out _A \cup out_B) \backslash shared (A,B) = \emptyset \), otherwise the system is open.
In distributed applications, implemented, e.g., with a message-passing middleware, usually an asynchronous communication pattern is used. In this paper, we consider asynchronous communication via unbounded message queues. In Fig. 1 two asynchronously communicating IOTSes A and B are depicted. A sends a message a to B by putting it, with action \(a^\rhd \), into a queue which stores the outputs of A. Then B can receive a by removing it, with action a, from the queue. In contrast to synchronous communication, there is a delay between sending and reception. Similarly, B can send a message b to A by using a second queue which stores the outputs of B. The system in Fig. 1 is open: A has an open output x to the environment and an open input y for messages coming from the environment. Similarly B has an open input u and an open output v. Additionally, A and B may have some internal actions.
To formalize asynchronous communication, we equip each communicating IOTS with an “output queue”, which leads to a new IOTS indicated in Fig. 1 by \(\varOmega (A)\) and \(\varOmega (B)\) respectively. For this construction, we represent an output queue as an (infinite) IOTS and then we compose it with a renamed version of A where all outputs a of A (to be stored in the queue) are renamed to enqueue actions of the form \(a^\rhd \).
Definition 3
(IOTS with output queue).
-
1.
Let M be a set of names and \(M^\rhd = \{ a^\rhd \mid a \in M\}\) be disjoint from M. The queue IOTS for M is \(Q_M = (M^*, \epsilon , act _{Q_M}, {\mathop {\longrightarrow }\limits ^{}\!\!\!{\genfrac{}{}{0.0pt}{}{}{Q_M}}})\) where the set of states is the set \(M^*\) of all words over M, the initial state \(\epsilon \in M^*\) is the empty word, and the set of actions \( act _{Q_M}\) is the disjoint union of input actions \( in _{Q_M} = M^\rhd \), output actions \( out _{Q_M} = M\) and with no internal action. The transition relation \({\mathop {\longrightarrow }\limits ^{}\!\!\!{\genfrac{}{}{0.0pt}{}{}{Q_M}}}\) is the smallest relation such that
-
for all \(a^\rhd \in M^\rhd \) and states \(q \in M^*: \ q \, {\mathop {\longrightarrow }\limits ^{a^\rhd }\!\!\!{\genfrac{}{}{0.0pt}{}{}{Q_M}}}\, qa\) (enqueue on the right),
-
for all \(a \in M\) and states \(q \in M^*: \ aq \, {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{Q_M}}}\, q\) (dequeue on the left).
-
-
2.
Let A be an IOTS such that \(M \subseteq out _A\) and \(M^\rhd \cap act _A = \emptyset \). Let \(A_{M}^\rhd \) be the renamed version of A where all \(a \in M\) are renamed to \(a^\rhd \). The IOTS A equipped with output queue for M is given by the synchronous composition \(\varOmega _{M}(A) = A_{M}^\rhd \otimes Q_M\). (Note that \(A_{M}^\rhd \) and \(Q_M\) are composable.)
The states of \(\varOmega _{M}(A)\) are pairs (s, q) where s is a state of A and q is a word over M. The initial state is \(( start _A,\epsilon )\). For the actions we have \( in _{\varOmega _{M}(A)} = in _A, out _{\varOmega _{M}(A)} = out _A\), and \( int _{\varOmega _{M}(A)} = int _A \cup M^\rhd \). Transitions in \(\varOmega _{M}(A)\) are:
-
if \(a \in in _A\) and \(s {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'\) then \((s,q) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega _{M}(A)}}} (s',q)\),
-
if \(a \in out _A \backslash M\) and \(s {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'\) then \((s,q) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega _{M}(A)}}} (s',q)\),
-
if \(a \in M \subseteq out _A\) then \((s,a q) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega _{M}(A)}}} (s,q) \),
-
if \(a \in int _A\) and \(s {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'\) then \((s,q) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega _{M}(A)}}} (s',q)\),
-
if \(a^\rhd \in M^\rhd \) and \(s {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'\) (i.e. \(s {\mathop {\longrightarrow }\limits ^{a^\rhd }\!\!\!{\genfrac{}{}{0.0pt}{}{}{A_{M}^\rhd }}} s'\)) then \((s,q) {\mathop {\longrightarrow }\limits ^{a^\rhd }\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega _{M}(A)}}} (s',q a) \).
To define the asynchronous composition of two IOTSes A and B, we assume that A and B are asynchronously composable which means that A and B are composable (as before) and \( shared (A,B)^\rhd \cap ( act _A \cup act _B) = \emptyset \). Then, we equip A with an output queue for those outputs shared with inputs of B, and, similarly, we equip B with an output queue for those outputs shared with inputs of A. The IOTSes \(\varOmega _{ out _A \cap in _B}(A)\) and \(\varOmega _{ out _B \cap in _A}(B)\) are then synchronously composed which gives the asynchronous composition of A and B.
Definition 4
(Asynchronous composition). Let A, B be two asynchronously composable IOTSes. The asynchronous composition of A and B is defined by \(A \otimes _{ as }B = \varOmega _{ out _A \cap in _B}(A) \otimes \varOmega _{ out _B \cap in _A}(B)\).Footnote 1
In the sequel we will briefly write \(\varOmega (A)\) for \(\varOmega _{ out _A \cap in _B}(A)\) and \(\varOmega (B)\) for \(\varOmega _{ out _B \cap in _A}(B)\). The states of \(\varOmega (A) \otimes \varOmega (B)\) are pairs \(((s_A,q_A),(s_B,q_B))\) where \(s_A\) is a state of A, the queue \(q_A\) stores elements of \( out _A \cap in _B\), \(s_B\) is a state of B, and the queue \(q_B\) stores elements of \( out _B \cap in _A\). The initial state is \((( start _A,\epsilon ),( start _B,\epsilon ))\). For the actions we have \( in _{\varOmega (A) \otimes \varOmega (B)} = in _{A \otimes B}\), \( out _{\varOmega (A) \otimes \varOmega (B)} = out _{A \otimes B}\), and \( int _{\varOmega (A) \otimes \varOmega (B)} = int _{A \otimes B} \cup shared (A,B)^\rhd \). For the transitions in \(\varOmega (A) \otimes \varOmega (B)\) we have two main cases:
-
1.
Transitions which can freely occur in A or in B without involving any output queue. These transitions change just the local state of A or of B. An example would be a transition \(s_A {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'_A\) with action \(a \in out _A \backslash in _B\) which induces a transition \(((s_A,q_A),(s_B,q_B)) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (A) \otimes \varOmega (B)}}}\) \(((s'_A,q_A),(s_B,q_B))\).
-
2.
Transitions which involve the output queue of A. There are two sub-cases concerning dequeue and enqueue actions which are internal actions in \(\varOmega (A) \otimes \varOmega (B)\):
-
(a)
\(a \in out _A \cap in _B\) (hence \(a \in out _{Q_{ out _A \cap in _B}}\)) and \(s_B {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} s'_B\) then \(((s_A,a q_A),(s_B,q_B)) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (A) \otimes \varOmega (B)}}} ((s_A,q_A),(s'_B,q_B))\).
-
(b)
\(a^\rhd \in ( out _A \cap in _B)^\rhd \) (hence \(a \in in _{Q_{ out _A \cap in _B}})\) and \(s_A {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'_A\) then \(((s_A,q_A),(s_B,q_B)) {\mathop {\longrightarrow }\limits ^{a^\rhd }\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (A) \otimes \varOmega (B)}}} ((s'_A,q_A a),(s_B,q_B))\).
Transitions which involve the output queue of B are analogous.
-
(a)
3 Compatibility Notions
In this section we review our compatibility notions introduced in [4] for the synchronous and in [3] for the asynchronous case. For synchronous compatibility the idea is that whenever a component wants to issue an output a then its communication partner should be ready to accept a as an input.
Definition 5
(Strong synchronous compatibility). Two IOTSes A and B are strongly synchronously compatible, denoted by  , if they are composable and if for all reachable states \((s_A,s_B) \in \mathcal {R}(A \otimes B)\),
, if they are composable and if for all reachable states \((s_A,s_B) \in \mathcal {R}(A \otimes B)\),
-
(1)
\(\forall a \in out _A \cap in _B : \ s_A {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'_A \Longrightarrow \exists \ s_B {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} s'_B\),
-
(2)
\(\forall a \in out _B \cap in _A : \ s_B {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} s'_B \Longrightarrow \exists \ s_A {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'_A\).
This definition requires that IOTSes should work properly together in any environment, in contrast to the “optimistic” approach of [11] in which the existence of a “helpful” environment to avoid error states is sufficient. For closed systems this makes no difference. In [4] we have introduced a weak version of compatibility such that a component can delay an expected input and perform some internal actions before. (This works well with weak refinement; see [4].)
Definition 6
(Weak synchronous compatibility). Two IOTSes A and B are weakly synchronously compatible, denoted by  , if they are composable and if for all reachable states \((s_A,s_B) \in \mathcal {R}(A \otimes B)\),
, if they are composable and if for all reachable states \((s_A,s_B) \in \mathcal {R}(A \otimes B)\),
-
(1)
\(\forall a \in out _A \cap in _B : \ s_A {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'_A \Longrightarrow \exists \ s_B \ {\xrightarrow {\, int _B\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{B}} \ \overline{s}_B {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} s'_B\),
-
(2)
\(\forall a \in out _B \cap in _A : \ s_B {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} s'_B \Longrightarrow \exists \ s_A \ {\xrightarrow {\, int _A\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{A}} \ \overline{s}_A {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'_A\),
Now we turn to compatibility of asynchronously communicating components. In this case outputs of a component are stored in a queue from which they can be consumed by the receiver component. Therefore, in the asynchronous context, compatibility means that if a queue is not empty, the receiver component must be ready to take (i.e. input) the next removable element from the queue. This idea can be easily formalized by requiring synchronous compatibility between the communicating IOTSes which are enhanced by their output queues. We distinguish again between strong and weak compatibility versions.
Definition 7
(Strong and weak asynchronous compatibility). Let A and B be two asynchronously composable I/O-transition systems. A and B are strongly asynchronously compatible, denoted by  , if
, if  . A and B are weakly asynchronously compatible, denoted by
. A and B are weakly asynchronously compatible, denoted by  , if
, if  .
.
Example 1
Figure 2 shows the behavior of a Maker and a User process. Here and in the subsequent drawings we use the following notations: Initial states are denoted by 0, input actions a are indicated by a?, output actions a by a!, and internal actions a by \(\tau _a\). The maker expects some material from the environment (input action material), constructs some item (internal action make), and then it signals either that the item is ready (output action ready) or that the production did fail (output action fail). Both actions are shared with input actions of the user. When the user has received the ready signal it uses the item (internal action use). Maker and User are weakly synchronously compatible but not strongly synchronously compatible. The critical state in the synchronous product Maker \(\otimes \) User is (2,1) which can be reached with the transitions  .
.
In this state the maker wants to send ready or fail but the user must first perform its internal use action before it can receive the corresponding input. The asynchronous composition Maker \(\otimes _{ as }\) User has infinitely many states since the maker can be faster then the user. We will see, as an application of the forthcoming results, that Maker and User are also weakly asynchronously compatible.
4 Relating Synchronous and Asynchronous Compatibility
We are now interested in possible relationships between synchronous and asynchronous compatibility. This is particularly motivated by the fact that for finite IOTSes reachability, and therefore synchronous (strong and weak) compatibility, are decidable which is in general not the case for asynchronous communication with unbounded FIFO-buffers.
4.1 From Synchronous to Asynchronous Compatibility
In this section we study conditions under which it is sufficient to check strong (weak) synchronous compatibility to ensure strong (weak) asynchronous compatibility. In general this implication does not hold. As an example consider the two IOTSes A and B in Fig. 3. Obviously, A and B are strongly synchronously compatible. They are, however, not strongly asynchronously compatible since A may first put a in its output queue, then B can output b in its queue and then both are blocked (A can only accept \(\texttt {ack\_a}\) while B can only accept \(\texttt {ack\_b}\)). In Fig. 3 each IOTS has a state (the initial state) where a choice between an output and an input action is possible. We will see (Corollary 1) that if such situations are avoided synchronous compatibility implies asynchronous compatibility, and we will even get more general criteria (Theorem 1) for which the following property \(\mathcal {P}\) is important.
Property \(\mathcal {P}\): Let A and B be two asynchronously composable IOTSes. The asynchronous system \(A \otimes _{ as }B\) satisfies property \(\mathcal {P}\) if for each reachable state \(((s_A,q_A),(s_B,q_B)) \in \mathcal {R}(\varOmega (A) \otimes \varOmega (B))\) one of the following conditions holds:
-
(i)
\(q_A = q_B = \epsilon \) and \((s_A,s_B) \in \mathcal {R}(A \otimes B)\).
-
(ii)
\(q_A = a_1 \ldots a_m \ne \epsilon \) and \(q_B = \epsilon \) and there exists \(r_A \in states _A\) such that: \((r_A,s_B) \in \mathcal {R}(A \otimes B)\) and \(r_A {\mathop {\Longrightarrow }\limits ^{a_1}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} \ldots {\mathop {\Longrightarrow }\limits ^{a_m}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s_A\).
-
(iii)
\(q_A = \epsilon \) and \(q_B = b_1 \ldots b_m \ne \epsilon \) and there exists \(r_B \in states _B\) such that: \((s_A,r_B) \in \mathcal {R}(A \otimes B)\) and \(r_B {\mathop {\Longrightarrow }\limits ^{b_1}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} \ldots {\mathop {\Longrightarrow }\limits ^{b_m}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} s_B\).
To explain the notation \({\mathop {\Longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}}\), let \(a \in out _A \cap in _B\) and \(F_A = act _A \backslash shared (A,B)\) be the set of the free actions of A. Then \(s {\mathop {\Longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'\) stands for a sequence of transitions \(s {\xrightarrow {\,F_A\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{A}} \overline{s} {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}}\overline{s}' {\xrightarrow {\,F_A\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{A}} s'\) such that the transition with \(a \in out _A \cap in _B\) is surrounded by arbitrary transitions in A involving only free actions of A. The notation \({\mathop {\Longrightarrow }\limits ^{b}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}}\) is defined analogously.
Property \(\mathcal {P}\) expresses that (a) in each reachable state of the asynchronous composition at least one of the two queues is empty and (b) the state of the component where the output queue is not empty can be reached from a reachable state in the synchronous product by outputting the actions stored in the queue, possibly interleaved with free actions. Part (a) specifies half-duplex systems; see, e.g., [9].
Definition 8
Let A and B be two asynchronously composable IOTSes. The asynchronous system \(A \otimes _{ as }B\) is half-duplex, if for all reachable states \(((s_A,q_A),(s_B,q_B)) \in \mathcal {R}(\varOmega (A) \otimes \varOmega (B))\) it holds that \(q_A = \epsilon \) or \(q_B = \epsilon \).
It turns out that also part (b) explained above holds for half-duplex systems, i.e. property \(\mathcal {P}\) characterizes this class of systems as stated in Lemma 1, (1) and (2). In [9] it is shown that membership is decidable for half-duplex systems. This corresponds to condition (3) of Lemma 1 which says that in the synchronous product of A and B there is no reachable state where at the same time an output from A to B and an output from B to A is enabled. Obviously this is decidable for finite A and B.
Lemma 1
Let A and B be two asynchronously composable IOTSes. The following conditions are equivalent:
-
1.
The asynchronous system \(A \otimes _{ as }B\) satisfies property \(\mathcal {P}\).
-
2.
The asynchronous system \(A \otimes _{ as }B\) is half-duplex.
-
3.
For each reachable state \((s_A,s_B) \in \mathcal {R}(A \otimes B)\) and each transitions \(s_A {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'_A\) and \(s_B {\mathop {\longrightarrow }\limits ^{b}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} s'_B\) either \(a \notin out _A \cap in _B\) or \(b \notin out _B \cap in _A\).
Proof
(1) \(\Rightarrow \) (2) is trivial. (2) \(\Rightarrow \) (3) is straightforward by contradiction. The direction (3) \(\Rightarrow \) (1) is non-trivial. It involves a complex case distinction on the form of the transitions in the asynchronous composition. Interestingly only the case of transitions with enqueue actions needs the assumption (3). \(\square \)
Theorem 1
Let A and B be two asynchronously composable IOTSes such that one (and hence all) of the conditions in Lemma 1 are satisfied. Then the following holds:
-
1.
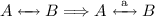 .
. -
2.
 .
.
Proof
The proof uses Lemma 1 for both cases. (1) Assume  . We have to show
. We have to show  . We prove condition (1) of Definition 5. Condition (2) is proved analogously. Let \(((s_A,q_A),(s_B,q_B)) \in \mathcal {R}(\varOmega (A) \otimes \varOmega (B))\), \(a \in out _{\varOmega (A)} \cap in _{\varOmega (B)}\) and \( (s_A,q_A) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (A)}}} (s'_A,q'_A)\). Then \(q_A\) has the form \(a a_2 \ldots a_m\). By assumption, \(\varOmega (A) \otimes \varOmega (B)\) satisfies the property \(\mathcal {P}\). Hence, there exists \(r_A \in states _A\) such that \((r_A,s_B) \in \mathcal {R}(A \otimes B)\) and \(r_A {\mathop {\Longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} \overline{r}_A {\mathop {\Longrightarrow }\limits ^{a_2}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\ldots }}}{\mathop {\Longrightarrow }\limits ^{a_m}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s_A\). Thereby \(r_A {\mathop {\Longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} \overline{r}_A\) is of the form \(r_A {\xrightarrow {\,F_A\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{A}} s {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s' {\xrightarrow {\,F_A\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{A}} \overline{r}_A\). Since \(F_A\) involves only free actions of A (not shared with B), and since \((r_A,s_B) \in \mathcal {R}(A \otimes B)\) we have that \((s,s_B) \in \mathcal {R}(A \otimes B)\). Now we can use the assumption
. We prove condition (1) of Definition 5. Condition (2) is proved analogously. Let \(((s_A,q_A),(s_B,q_B)) \in \mathcal {R}(\varOmega (A) \otimes \varOmega (B))\), \(a \in out _{\varOmega (A)} \cap in _{\varOmega (B)}\) and \( (s_A,q_A) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (A)}}} (s'_A,q'_A)\). Then \(q_A\) has the form \(a a_2 \ldots a_m\). By assumption, \(\varOmega (A) \otimes \varOmega (B)\) satisfies the property \(\mathcal {P}\). Hence, there exists \(r_A \in states _A\) such that \((r_A,s_B) \in \mathcal {R}(A \otimes B)\) and \(r_A {\mathop {\Longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} \overline{r}_A {\mathop {\Longrightarrow }\limits ^{a_2}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\ldots }}}{\mathop {\Longrightarrow }\limits ^{a_m}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s_A\). Thereby \(r_A {\mathop {\Longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} \overline{r}_A\) is of the form \(r_A {\xrightarrow {\,F_A\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{A}} s {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s' {\xrightarrow {\,F_A\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{A}} \overline{r}_A\). Since \(F_A\) involves only free actions of A (not shared with B), and since \((r_A,s_B) \in \mathcal {R}(A \otimes B)\) we have that \((s,s_B) \in \mathcal {R}(A \otimes B)\). Now we can use the assumption  which says that there exists \(s_B {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} s'_B\). Since \(a \in in _B\), we get a transition \((s_B,q_B) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (B)}}} (s'_B,q_B)\) and we are done.
which says that there exists \(s_B {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} s'_B\). Since \(a \in in _B\), we get a transition \((s_B,q_B) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (B)}}} (s'_B,q_B)\) and we are done.
(2) The weak case is a slight generalization of the proof of (1). The first part of the proof is the same but then we use the assumption  which says that there exists \(s_B \ {\xrightarrow {\, int _B\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{B}} \ \overline{s}_B {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} s'_B\) consisting of a sequence of internal transitions of B followed by \(\overline{s}_B {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} s'_B\) with \(a \in in _B\). Therefore we get transitions \((s_B,q_B) \ {\xrightarrow {\, int _B\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{\varOmega (B)}} \ (\overline{s}_B,q_B)\) \({\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (B)}}} (s'_B,q_B)\) and, since \( int _B \subseteq int _{\varOmega (B)}\) we are done. \(\square \)
which says that there exists \(s_B \ {\xrightarrow {\, int _B\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{B}} \ \overline{s}_B {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} s'_B\) consisting of a sequence of internal transitions of B followed by \(\overline{s}_B {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} s'_B\) with \(a \in in _B\). Therefore we get transitions \((s_B,q_B) \ {\xrightarrow {\, int _B\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{\varOmega (B)}} \ (\overline{s}_B,q_B)\) \({\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (B)}}} (s'_B,q_B)\) and, since \( int _B \subseteq int _{\varOmega (B)}\) we are done. \(\square \)
We come back to our discussion at the beginning of this section where we have claimed that for I/O-transition systems which do not show states where input and output actions are both enabled, synchronous compatibility implies asynchronous compatibility. We must, however, be careful whether we consider the strong or the weak case which leads us to two versions of I/O-separation.
Definition 9
(I/O-separated transition systems). Let A be an IOTS.
-
1.
A is called I/O-separated if for all reachable states \(s \in \mathcal {R}(A)\) it holds: If there exists a transition \(s {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'\) with \(a \in out _A\) then there is no transition \(s {\mathop {\longrightarrow }\limits ^{a'}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'\) with \(a' \in in _A\).
-
2.
A is called observationally I/O-separated if for all reachable states \(s \in \mathcal {R}(A)\) it holds: If there exists a transition \(s {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'\) with \(a \in out _A\) then there is no sequence of transitions \(s \ {\xrightarrow {\, int _A\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{A}} \ \overline{s}_A {\mathop {\longrightarrow }\limits ^{a'}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'\) with \(a' \in in _A\).
Obviously, observational I/O-separation implies I/O-separation but not the other way round.
Lemma 2
Let A and B be two asynchronously composable IOTSes.
-
1.
If A and B are I/O-separated and
 , then one (and hence all) of the conditions in Lemma 1 are satisfied.
, then one (and hence all) of the conditions in Lemma 1 are satisfied. -
2.
If A and B are observationally I/O-separated and
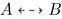 , then one (and hence all) of the conditions in Lemma 1 are satisfied.
, then one (and hence all) of the conditions in Lemma 1 are satisfied.
Proof
The proof of both cases is by contradiction. \(\square \)
The notion of I/O-separation appears in a more strict version, called input-separation, in [13] and similarly as system without local mixed states in [9]. Part (1) of Lemma 2 can be considered as a generalization of Lemma 4 in [13] which has shown that input-separated IOTSes which are strongly compatible and form a closed system are half-duplex. This result was in turn a generalization of Theorem 35 in [9]. Open systems and weak compatibility were not an issue in these approaches. With Theorem 1 and Lemma 2 we get:
Corollary 1
Let A and B be two asynchronously composable IOTSes.
-
1.
If A and B are I/O-separated and
 , then
, then  .
. -
2.
If A and B are observationally I/O-separated and
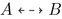 , then
, then 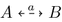 .
.
Let us note that part (2) of Corollary 1 would not hold, if we would only assume I/O-separation. As an application of Corollary 1 we refer to Example 1. Maker and User are observationally I/O-separated, they are weakly synchronously compatible and therefore, by Corollary 1(2), they are also weakly asynchronously compatible.
4.2 From Asynchronous to Synchronous Compatibility
This section studies the other direction, i.e. whether asynchronous compatibility can imply synchronous compatibility. It turns out that for the strong case this is indeed true without any further assumptions while for the weak case this holds under the equivalent conditions of Lemma 1. In any case, we need for the proof the following lemma which shows that all reachable states in the synchronous product are reachable in the asynchronous product with empty output queues.
Lemma 3
Let A and B be two asynchronously composable IOTSes. For any state \((s_A,s_B) \in \mathcal {R}(A \otimes B)\), the state \(((s_A,\epsilon ), (s_B,\epsilon ))\) belongs to \(\mathcal {R}(\varOmega (A) \otimes \varOmega (B))\).
Proof
The proof is straightforward by induction on the length of the derivation of \((s_A,s_B) \in \mathcal {R}(A \otimes B)\). \(\square \)
Theorem 2
For asynchronously composable IOTSes A and B it holds:
-
1.
 .
. -
2.
If one (and hence all) of the conditions in Lemma 1 are satisfied, then
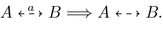 .
.
Proof
(1) Assume  , i.e.
, i.e.  . We have to show
. We have to show  . We prove condition (1) of Definition 5. Condition (2) is analogous.
. We prove condition (1) of Definition 5. Condition (2) is analogous.
Let \((s_A,s_B) \in \mathcal {R}(A \otimes B), a \in out _A \cap in _B\) and \(s_A {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'_A\). By Lemma 3, \(((s_A,\epsilon ), (s_B,\epsilon ))\) \(\in \mathcal {R}(\varOmega (A) \otimes \varOmega (B))\). Since \(s_A {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'_A\), we have a transition in \(\varOmega (A) \otimes \varOmega (B)\) with enqueue action for a: \(((s_A,\epsilon ), (s_B,\epsilon )) {\mathop {\longrightarrow }\limits ^{a^\rhd }\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (A) \otimes \varOmega (B)}}} ((s'_A,a), (s_B,\epsilon ))\) and it holds \(((s'_A,a), (s_B,\epsilon )) \in \mathcal {R}(\varOmega (A) \otimes \varOmega (B))\). Then, there is a transition \((s'_A,a) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (A)}}}\) \((s'_A,\epsilon )\). Since  there must be a transition \((s_B,\epsilon ) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (B)}}} (s'_B,\epsilon )\). This transtion must be caused by a transition \( s_B {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} s'_B\) and we are done.
there must be a transition \((s_B,\epsilon ) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (B)}}} (s'_B,\epsilon )\). This transtion must be caused by a transition \( s_B {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} s'_B\) and we are done.
(2) Assume  , i.e.
, i.e.  . We have to show
. We have to show  . We prove condition (1) of Definition 6. Condition (2) is proved analogously.
. We prove condition (1) of Definition 6. Condition (2) is proved analogously.
Let \((s_A,s_B) \in \mathcal {R}(A \otimes B), a \in out _A \cap in _B\) and \(s_A {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'_A\). With the same reasoning as in case (1) we get \(((s'_A,a), (s_B,\epsilon )) \in \mathcal {R}(\varOmega (A) \otimes \varOmega (B))\) and we get a transition \((s'_A,a) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (A)}}}\) \((s'_A,\epsilon )\). Since  there are transitions \((s_B,\epsilon )\ {\xrightarrow {\, int _{\varOmega (B)}\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{\varOmega (B)}}\ \) \((\overline{s}_B,\overline{q}_B) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (B)}}} (s'_B,\overline{q}_B)\). Since internal transitions of \(\varOmega (B)\) do not involve any steps of \(\varOmega (A)\), we have \(((s'_A,a), (\overline{s}_B,\overline{q}_B)) \in \mathcal {R}(\varOmega (A) \otimes \varOmega (B))\). Due to the assumption that the conditions in Lemma 1 are satisfied, \(\varOmega (A) \otimes \varOmega (B)\) is half-duplex and therefore \(\overline{q}_B\) must be empty and the same holds for all intermediate queues reached by the transitions in \((s_B,\epsilon )\ {\xrightarrow {\, int _{\varOmega (B)}\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{\varOmega (B)}} \ (\overline{s}_B,\overline{q}_B)\). Therefore no enqueue action can occur in these transitions. Noticing that \( int _{\varOmega (B)} = int _B \cup ( out _B \cap in _A)^\rhd \), we get \((s_B,\epsilon )\ {\xrightarrow {\, int _B\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{\varOmega (B)}} (\overline{s}_B,\epsilon ) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (B)}}} (s'_B,\epsilon )\) and all these transtions must be induced by transitions \(s_B \ {\xrightarrow {\, int _B\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{B}} \ \overline{s}_B {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} s'_B\), i.e. we are done. \(\square \)
there are transitions \((s_B,\epsilon )\ {\xrightarrow {\, int _{\varOmega (B)}\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{\varOmega (B)}}\ \) \((\overline{s}_B,\overline{q}_B) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (B)}}} (s'_B,\overline{q}_B)\). Since internal transitions of \(\varOmega (B)\) do not involve any steps of \(\varOmega (A)\), we have \(((s'_A,a), (\overline{s}_B,\overline{q}_B)) \in \mathcal {R}(\varOmega (A) \otimes \varOmega (B))\). Due to the assumption that the conditions in Lemma 1 are satisfied, \(\varOmega (A) \otimes \varOmega (B)\) is half-duplex and therefore \(\overline{q}_B\) must be empty and the same holds for all intermediate queues reached by the transitions in \((s_B,\epsilon )\ {\xrightarrow {\, int _{\varOmega (B)}\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{\varOmega (B)}} \ (\overline{s}_B,\overline{q}_B)\). Therefore no enqueue action can occur in these transitions. Noticing that \( int _{\varOmega (B)} = int _B \cup ( out _B \cap in _A)^\rhd \), we get \((s_B,\epsilon )\ {\xrightarrow {\, int _B\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{\varOmega (B)}} (\overline{s}_B,\epsilon ) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (B)}}} (s'_B,\epsilon )\) and all these transtions must be induced by transitions \(s_B \ {\xrightarrow {\, int _B\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{B}} \ \overline{s}_B {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} s'_B\), i.e. we are done. \(\square \)
As a consequence of Theorems 1, 2 we see that under the equivalent conditions of Lemma 1, in particular when the asynchronous system is half-duplex, (weak) synchronous compatibility is equivalent to (weak) asynchronous compatibility.
5 Weak Asynchronous Compatibility: The General Case
In this section we are interested in the verification of asynchronous compatibility in the general case, where at the same time both queues of the communicating IOTSes may be not empty. We focus here on weak asynchronous compatibility since non-half duplex systems are often weakly asynchronously compatible but not weakly synchronously compatible.Footnote 2 A simple example would be two components which both start to send a message to each other and after that each component takes the message addressed to it from the buffer.
Example 2
Figure 4 shows two IOTSes MA and MB which produce items for each other. After reception of some material from the environment, MA produces an item (internal action makeA) followed by either a signal that the item is ready for use (output readyA) or a signal that the production did fail (output failA). Whenever MA reaches its initial state it can also accept an input readyB and then use the item produced by MB (internal action useB) or it can accept a signal that the production of its partner did fail (input failB). The behavior of MB is analogous. The asynchronous composition of MA and MB is not half-duplex; both processes can produce and signal concurrently. Clearly, the system is not weakly synchronously compatible. For instance, the state (2,2) is reachable in the synchronous product and in this state each of the two processes wants to output an action which the other is not able to accept. The system is also not synchronizable in the sense of [15]. We will prove below that the system is weakly asynchronously compatible.
In general, the problem of weak asynchronous compatibility is undecidable due to the unbounded message queues. We develop in the following a criterion, which is decidable if the underlying IOTSes are finite, which works for non half-duplex systems, and which ensures weak asynchronous compatibility. The idea is to use again synchronous products, but not the standard synchronous composition of two IOTSes A and B but variants of it. First we focus only on one direction of compatibility concerning the outputs of A which should be received by B. Due to the weak compatibility notion B can, before it takes an input message, execute internal actions. In particular, it can put outputs directed to A in its output queue. (Remember that enqueue actions are internal). To simulate this in a synchronous product we must artificially hide these outputs of B such that they become free actions in the synchronous product. Consequently also the corresponding inputs of A must be hidden. Then we require that outputs of A directed to B can be received by B possibly after some internal actions are executed, which now subsumes also the hidden outputs of B. A symmetric requirement is obtained when we consider compatibility in the direction from B to A. For the formalization of these ideas we first define hiding of actions.
Definition 10
(Hiding). Let \(A = ( states _A, start _A, act _A,{\mathop {\longrightarrow }\limits ^{}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}})\) be an IOTS and \(H \subseteq in _A \cup out _A\). The hiding of H in A yields the IOTS  where
where  is the disjoint union of the input actions
is the disjoint union of the input actions  , the output actions
, the output actions  , and the internal actions
, and the internal actions  .
.
Taking the synchronous compositions of IOTSes with hidden actions we can formulate our requirements explained above by the following (symmetric) conditions (a) and (b). Let A and B be two asynchronously composable IOTSes, let \( out _{ BA }= out _B \cap in _A\) and \( out _{ AB }= out _A \cap in _B\).
-
(a)
For all reachable states
 ,
, 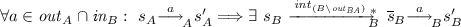 .
. -
(b)
For all reachable states
 ,
,  .
.
Notation: We write \(A \backslash out _{ BA }\dashrightarrow B \backslash out _{ BA }\) if condition (a) holds and \(B \backslash out _{ AB }\dashrightarrow A \backslash out _{ AB }\) if condition (b) holds.
Concerning (a), the essential difference between \(A \otimes B\) and \(A \backslash out _{ BA }\otimes B \backslash out _{ BA }\) is that shared actions belonging to \( out _{ BA }= out _B \cap in _A\) must synchronize in \(A \otimes B\) while they can occur freely in \(A \backslash out _{ BA }\otimes B \backslash out _{ BA }\) whenever A or B can perform one of them. Hence \(A \backslash out _{ BA }\otimes B \backslash out _{ BA }\) can have significantly more reachable states than \(A \otimes B\), in particular the ones reached by autonomous outputs of B directed to A. These states are often relevant in the asynchronous composition of A and B since outputs of B directed to A are internally put in the output queue of B. The same reasoning holds symmetrically for condition (b).
The following lemma, used for the proof of Theorem 3, establishes an important relationship between the reachable states considered in the synchronous products after hiding and those of the asynchronous composition of A and B. The properties \(\mathcal {Q}_A\) and \(\mathcal {Q}_B\) stated in the lemma have a pattern similar to property \(\mathcal {P}\) in Sect. 4.1. In contrast to property \(\mathcal {P}\) they are generally valid.
Lemma 4
For any two asynchronously composable IOTSes A and B both of the following two properties \(\mathcal {Q}_A\) and \(\mathcal {Q}_B\) are satisfied.
Property \(\mathcal {Q}_A\): For each reachable state \(((s_A,q_A),(s_B,q_B)) \in \mathcal {R}(\varOmega (A) \otimes \varOmega (B))\) one of the following two conditions holds:
-
(i)
\(q_A = \epsilon \) and \((s_A,s_B) \in \mathcal {R}(A \backslash out _{ BA }\otimes B \backslash out _{ BA })\),
-
(ii)
\(q_A = a_1 \ldots a_m \ne \epsilon \) and there exists \(r_A \in states _A\) such that: \((r_A,s_B) \in \mathcal {R}(A \backslash out _{ BA }\otimes B \backslash out _{ BA })\) and \(r_A \mathop {\Rrightarrow }\limits ^{a_1}_{_{ A }} \ldots \mathop {\Rrightarrow }\limits ^{a_m}_{_{ A }} s_A\).
The notation \(s \mathop {\Rrightarrow }\limits ^{a}_{_{ A }} s'\) stands for an arbitrary sequence of transitions in A which contains exactly one transition with an output action in \( out _A \cap in _B\) and this output action is a.
Property \(\mathcal {Q}_B\): For each reachable state \(((s_A,q_A),(s_B,q_B)) \in \mathcal {R}(\varOmega (A) \otimes \varOmega (B))\) one of the following two conditions holds:
-
(i)
\(q_B = \epsilon \) and \((s_A,s_B) \in \mathcal {R}(A \backslash out _{ AB }\otimes B \backslash out _{ AB })\),
-
(ii)
\(q_B = b_1 \ldots b_m \ne \epsilon \) and there exists \(r_B \in states _B\) such that: \((s_A,r_B) \in \mathcal {R}(A \backslash out _{ AB }\otimes B \backslash out _{ AB })\) and \(r_B \mathop {\Rrightarrow }\limits ^{b_1}_{_{ B }} \ldots \mathop {\Rrightarrow }\limits ^{b_m}_{_{ B }} s_B\). The notation \( \mathop {\Rrightarrow }\limits ^{b}_{_{ B }} \) is defined analogously to \( \mathop {\Rrightarrow }\limits ^{a}_{_{ A }} \).
Proof
The initial state \((( start _A,\epsilon ),( start _B,\epsilon ))\) satisfies \(\mathcal {Q}_A\) and \(\mathcal {Q}_B\). Then we consider transitions \( ((s_A,q_A),(s_B,q_B)) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (A) \otimes \varOmega (B)}}} ((s'_A,q'_A),(s'_B,q'_B))\) and show that if \( ((s_A,q_A),(s_B,q_B))\) satisfies \(\mathcal {Q}_A\) (\(\mathcal {Q}_B\) resp.) then \(((s'_A,q'_A),(s'_B,q'_B))\) satisfies \(\mathcal {Q}_A\) (\(\mathcal {Q}_B\) resp.). Then the result follows by induction on the length of the derivation to reach \(((s_A,q_A),(s_B,q_B)) \in \mathcal {R}(\varOmega (A) \otimes \varOmega (B))\). \(\square \)
Property \(\mathcal {Q}_A\)(ii) shows that a state of component A where the output queue is not empty can be reached from a state in the synchronous product of \(A \backslash out _{ BA }\) and \(B \backslash out _{ BA }\) by outputting the actions stored in the queue, possibly interleaved with arbitrary other actions of A which are not output actions directed to B. Property \(\mathcal {Q}_B\)(ii) is the symmetric property concerning the output queue of B.
Theorem 3
Let A and B be two asynchronously composable IOTSes such that \(A \backslash out _{ BA }\dashrightarrow B \backslash out _{ BA }\) and \(B \backslash out _{ AB }\dashrightarrow A \backslash out _{ AB }\) holds. Then A and B are weakly asynchronously compatible, i.e.  .
.
Proof
The proof relies on Lemma 4. We prove condition (1) of Definition 6. Condition (2) is proved analogously.
Let \(((s_A,q_A),(s_B,q_B)) \in \mathcal {R}(\varOmega (A) \otimes \varOmega (B))\), \(a \in out _{\varOmega (A)} \cap in _{\varOmega (B)}\) and \((s_A,q_A) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (A)}}}\) \((s'_A,q'_A)\). Then \(q_A\) has the form \(a a_2 \ldots a_m\). By Lemma 4, property \(\mathcal {Q}_A\)(ii) holds. Hence, there exists \(r_A \in states _A\) such that \((r_A,s_B) \in \mathcal {R}(A \backslash out _{ BA }\otimes B \backslash out _{ BA })\) and \(r_A \mathop {\Rrightarrow }\limits ^{a}_{_{ A }} \overline{r}_A \mathop {\Rrightarrow }\limits ^{a_2}_{_{ A }} \ldots \mathop {\Rrightarrow }\limits ^{a_m}_{_{ A }} s_A\). Thereby \(r_A \mathop {\Rrightarrow }\limits ^{a}_{_{ A }} \overline{r}_A\) is of the form \(r_A {\xrightarrow {\,Y_A\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{A}} s {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'\) \({\xrightarrow {\,Y_A\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{A}} \overline{r}_A\) with \(a \in out _A \cap in _B\) and \(Y_A\) involves no action in \( out _{ AB }= out _A \cap in _B\). Since \( out _{ AB }\) are the only shared actions of \(A \backslash out _{ BA }\) and \(B \backslash out _{ BA }\), the transitions in \(r_A {\xrightarrow {\,Y_A\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{A}} s\) induce transitions in \(A \backslash out _{ BA }\otimes B \backslash out _{ BA }\) without involving B. Therefore, since \((r_A,s_B) \in \mathcal {R}(A \backslash out _{ BA }\otimes B \backslash out _{ BA })\), we get \((s,s_B) \in \mathcal {R}(A \backslash out _{ BA }\otimes B \backslash out _{ BA })\). Now we can use the assumption \(A \backslash out _{ BA }\dashrightarrow B \backslash out _{ BA }\) which says that there exists \(s_B \ {\xrightarrow {\, int _{(B \backslash out _{ BA })}\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{B}} \ \overline{s}_B {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} s'_B\) consisting of a sequence of internal transitions in \(B \backslash out _{ BA }\) followed by \(\overline{s}_B {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{B}}} s'_B\) with \(a \in in _B\). Now we notice that the internal actions of \(B \backslash out _{ BA }\) are either internal in B, and hence in \(\varOmega (B)\), or they are actions \(b \in out _{ BA }= out _B \cap in _A\), which induce internal enqueue actions \(b^\rhd \) in \(\varOmega (B)\). Thus we get transitions \((s_B,q_B) \ {\xrightarrow {\, int _{\varOmega (B)}\,}}\!\!\!{\genfrac{}{}{0.0pt}{}{*}{\varOmega (B)}} \ \) \((\overline{s}_B,\overline{q}_B) {\mathop {\longrightarrow }\limits ^{a}\!\!\!{\genfrac{}{}{0.0pt}{}{}{\varOmega (B)}}} (s'_B,\overline{q}_B)\) (where \(\overline{q}_B\) extends \(q_B\) according to the elements that have been enqueued with internal enqueue actions). Thus \(\varOmega (B)\) accepts a, possibly after some internal actions, and we are done. \(\square \)
Example 3
To apply Theorem 3 to Example 2 we have to prove \(\texttt {MA} \backslash \{\texttt {readyB,failB}\} \dashrightarrow {\texttt {MB}} \backslash \{\texttt {readyB,failB}\}\) and \(\texttt {MB} \backslash \{\texttt {readyA,failA}\} \dashrightarrow \texttt {MA} \backslash \{\texttt {readyA,failA}\}\). For the former case, Fig. 5 shows the IOTS MA after hiding its inputs readyB,failB shared with outputs of MB and the IOTS MB after hiding its outputs. We will check only this case, the other one is analogous. We have to consider the reachable states in the synchronous product \(\texttt {MA} \backslash \{\texttt {readyB,failB}\} \otimes \texttt {MB} \backslash \{\texttt {readyB,failB}\}\) and when an output readyA or failA is possible in \(\texttt {MA} \backslash \{\texttt {readyB,failB}\}\). These states are (2,0), (2,1), (2,2) and also (2,3). In state (2,0) any output readyA or failA is immediately accepted. In all other states \(\texttt {MB} \backslash \{\texttt {readyB,failB}\}\) can perform some internal actions first before it accepts readyA or failA. Hence, \(\texttt {MA} \backslash \{\texttt {readyB,failB}\} \dashrightarrow \texttt {MB} \backslash \{\texttt {readyB,failB}\}\) holds. We want to point out particularly state (2,2). In this state \(\texttt {MB} \backslash \{\texttt {readyB,failB}\}\) can perform the internal action \(\tau _{\texttt {readyB!}}\) before accepting readyA or failA. The internal action \(\tau _{\texttt {readyB!}}\) has been obtained from hiding the output action readyB in MB. In this way we have simulated in the synchronous product the (internal) enqueue action \(\texttt {readyB}^\rhd \) that would have happened by MB in the asynchronous composition.Footnote 3
6 Conclusion
We have proposed techniques to verify asynchronous compatibility by using criteria that are based on synchronous composition. Our results lead to the following verification methodology: Assume given two asynchronously communicating components, each one having finitely many local states. First we check whether condition (3) of Lemma 1 holds (in the synchronous product) which is decidable. It characterizes half-duplex systems. If the answer is positive, then we can decide strong and weak asynchronous compatibility using Theorems 1 and 2. If the answer is negative, then our system is not half-duplex. In this case we check the decidable conditions formulated in Theorem 3. If they are satisfied then the system is weakly asynchronously compatible. If they are not satisfied then all examples we have considered so far were in fact not weakly asynchronously compatible; but since the problem is undecidable we cannot expect that this is always the case. To illustrate this issue we consider a simple example with two components A and B such that A has one input action a and one output action b, and B has one input action b and one output action a. A has three states and the following two transitions \( start _A {\mathop {\longrightarrow }\limits ^{a?}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s'_A {\mathop {\longrightarrow }\limits ^{b!}\!\!\!{\genfrac{}{}{0.0pt}{}{}{A}}} s''_A\). B has only the initial state \( start _B\) and no transition. Then it is trivial that A and B are weakly asynchronously compatible, since in the asynchronous composition A will never receive a message from B and therefore A will never put b in its output buffer. However, our criterion \(A \backslash out _{ BA }\dashrightarrow B \backslash out _{ BA }\) is not satisfied since \( out _{ BA }= \{a\}\) is hidden in \(A \backslash out _{ BA }\) and therefore the state \((s'_A, start _B)\) is reachable in \(\mathcal {R}(A \backslash out _{ BA }\otimes B \backslash out _{ BA })\). Then \(A \backslash out _{ BA }\dashrightarrow B \backslash out _{ BA }\) would require that \(B \backslash out _{ BA }\) is able to receive b in its initial state which is not the case. As a consequence of this discussion our conjecture is that the criterion of Theorem 3 may not work only if there are states in which one component has a transition with an output action which will never be executed in the composition due to missing input before.
The verification conditions studied in this paper involve only synchronous compatibility checking. Therefore we can use the MIO Workbench [4], an Eclipse-based verification tool for modal I/O-transition systems, to verify asynchronous compatibility.
Theorem 3 relies on Lemma 4 which is generally valid and could be used to support the verification of other compatibility problems as well, e.g., to prove that a component waiting for some input will eventually get it. It would also be interesting to see to what extent our techniques can be applied to the optimistic compatibility notion used for interface automata [11] if they are put in an asynchronous environment. Concerning larger systems, the current approach suggests to add incrementally one component after the other and to verify compatibility in each step. But we also want to extend our work and study asynchronous compatibility of multi-component ensembles.
References
Basu, S., Bultan, T., Ouederni, M.: Deciding choreography realizability. In: Proceedings of ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL, pp. 191–202. ACM (2012)
Basu, S., Bultan, T., Ouederni, M.: Synchronizability for verification of asynchronously communicating systems. In: Kuncak, V., Rybalchenko, A. (eds.) VMCAI 2012. LNCS, vol. 7148, pp. 56–71. Springer, Heidelberg (2012)
Sebastian, S. B., Hennicker, R., Janisch, S.: Interface theories for (a)synchronously communicating modal I/O-transition systems. In: Proceedings of the Foundations for Interface Technologies, FIT, EPTCS 46, pp. 1–8 (2010)
Bauer, S.S., Mayer, P., Schroeder, A., Hennicker, R.: On weak modal compatibility, refinement, and the MIO workbench. In: Esparza, J., Majumdar, R. (eds.) TACAS 2010. LNCS, vol. 6015, pp. 175–189. Springer, Heidelberg (2010)
Beohar, H., Cuijpers, P.J.L.: Avoiding diamonds in desynchronisation. Sci. Comput. Program. 91, 45–69 (2014)
Brand, D., Zafiropulo, P.: On communicating finite-state machines. J. ACM 30(2), 323–342 (1983)
Canal, C., Pimentel, E., Troya, J.M.: Compatibility and inheritance in software architectures. Sci. Comput. Program. 41(2), 105–138 (2001)
Carmona, J., Kleijn, J.: Compatibility in a multi-component environment. Theor. Comput. Sci. 484, 1–15 (2013)
Cécé, G., Finkel, A.: Verification of programs with half-duplex communication. Inf. Comput. 202(2), 166–190 (2005)
Clemente, L., Herbreteau, F., Sutre, G.: Decidable Topologies for communicating automata with FIFO and bag channels. In: Baldan, P., Gorla, D. (eds.) CONCUR 2014. LNCS, vol. 8704, pp. 281–296. Springer, Heidelberg (2014)
de Alfaro, L., Henzinger, T.A.: Interface automata. In: Proceedings of the 9th ACM SIGSOFT Annual Symposium Foundations of Software Engineering (FSE 2001), pp. 109–120. ACM Press, Wien (2001)
Haddad, S., Hennicker, R., Møller, M.H.: Channel properties of asynchronously composed Petri nets. In: Colom, J.-M., Desel, J. (eds.) PETRI NETS 2013. LNCS, vol. 7927, pp. 369–388. Springer, Heidelberg (2013)
Hennicker, R., Janisch, S., Knapp, A.: Refinement of components in connection-safe assemblies with synchronous and asynchronous communication. In: Choppy, C., Sokolsky, O. (eds.) Monterey Workshop 2008. LNCS, vol. 6028, pp. 154–180. Springer, Heidelberg (2010)
Larsen, K.G., Nyman, U., Wąsowski, A.: Modal I/O automata for interface and product line theories. In: De Nicola, R. (ed.) ESOP 2007. LNCS, vol. 4421, pp. 64–79. Springer, Heidelberg (2007)
Ouederni, M., Salaün, G., Bultan, T.: Compatibility checking for asynchronously communicating software. In: Fiadeiro, J.L., Liu, Z., Xue, J. (eds.) FACS 2013. LNCS, vol. 8348, pp. 310–328. Springer, Heidelberg (2014)
Raclet, J.-B., Badouel, E., Benveniste, A., Caillaud, B., Legay, A., Passerone, R.: A modal interface theory for component-based design. Fundam. Inform. 108(1–2), 119–149 (2011)
Acknowledgement
We are very grateful to Alexander Knapp for his suggestion to use output queues (instead of input queues) for the formalization of asynchronous compatibility.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 IFIP International Federation for Information Processing
About this paper
Cite this paper
Hennicker, R., Bidoit, M., Dang, TS. (2016). On Synchronous and Asynchronous Compatibility of Communicating Components. In: Lluch Lafuente, A., Proença, J. (eds) Coordination Models and Languages. COORDINATION 2016. Lecture Notes in Computer Science(), vol 9686. Springer, Cham. https://doi.org/10.1007/978-3-319-39519-7_9
Download citation
DOI: https://doi.org/10.1007/978-3-319-39519-7_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-39518-0
Online ISBN: 978-3-319-39519-7
eBook Packages: Computer ScienceComputer Science (R0)










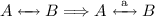 .
. .
. , then one (and hence all) of the conditions in Lemma
, then one (and hence all) of the conditions in Lemma 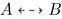 , then one (and hence all) of the conditions in Lemma
, then one (and hence all) of the conditions in Lemma  , then
, then  .
.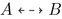 , then
, then 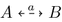 .
. .
.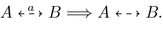 .
.
 but not
but not  .
. ,
, 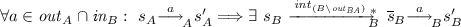 .
. ,
,  .
.