On Finite Monoids of Cellular Automata

Abstract

For any group G and set A, a cellular automaton over G and A is a transformation $\tau : A^G \rightarrow A^G$ defined via a finite neighbourhood $S \subseteq G$ (called a memory set of $\tau$) and a local function $\mu : A^S \rightarrow A$. In this paper, we assume that G and A are both finite and study various algebraic properties of the finite monoid $\mathrm {CA}(G,A)$ consisting of all cellular automata over G and A. Let $\mathrm {ICA}(G;A)$ be the group of invertible cellular automata over G and A. In the first part, using information on the conjugacy classes of subgroups of G, we give a detailed description of the structure of $\mathrm {ICA}(G;A)$ in terms of direct and wreath products. In the second part, we study generating sets of $\mathrm {CA}(G;A)$. In particular, we prove that $\mathrm {CA}(G,A)$ cannot be generated by cellular automata with small memory set, and, when G is finite abelian, we determine the minimal size of a set $V \subseteq \mathrm {CA}(G;A)$ such that $\mathrm {CA}(G;A) = \langle \mathrm {ICA}(G;A) \cup V \rangle$.

1 Introduction

Cellular automata (CA), first introduced by John von Neumann as an attempt to design self-reproducing systems, are models of computation with important applications to computer science, physics, and theoretical biology. In recent years, the theory of CA has been greatly enriched with its connections to group theory and topology (see [4] and references therein). One of the goals of this paper is to embark in the new task of exploring CA from the point of view of finite group and semigroup theory.

We review the broad definition of CA that appears in [4, Sect. 1.4]. Let G be a group and A a set. Denote by $A^G$ the configuration space, i.e. the set of all functions of the form $x:G \rightarrow A$. For each $g \in G$, let $R_g : G \rightarrow G$ be the right multiplication function, i.e. $(h)R_g := hg$, for any $h \in G$. We emphasise that we apply functions on the right, while in [4] functions are applied on the left.

Definition 1

Let G be a group and A a set. A cellular automaton over G and A is a transformation $\tau : A^G \rightarrow A^G$ such that there is a finite subset $S \subseteq G$, called a memory set of $\tau$, and a local function $\mu : A^S \rightarrow A$ satisfying

$$\begin{aligned} (g)(x)\tau = (( R_g \circ x )\vert _{S}) \mu , \ \forall x \in A^G, g \in G. \end{aligned}$$

Most of the classical literature on CA focuses on the case when $G=\mathbb {Z}^d$, for $d\ge 1$, and A is a finite set (e.g. see survey [11]).

A semigroup is a set M equipped with an associative binary operation. If there exists an element $\mathrm {id}\in M$ such that $\mathrm {id}\cdot m = m \cdot \mathrm {id}= m$, for all $m \in M$, the semigroup M is called a monoid and $\mathrm {id}$ an identity of M. Clearly, the identity of a monoid is always unique.

Let $\mathrm {CA}(G;A)$ be the set of all cellular automata over G and A; by [4, Corollary 1.4.11], this set equipped with the composition of functions is a monoid. Although results on monoids of CA have appeared in the literature before (see [3, 9, 12]), the algebraic structure of $\mathrm {CA}(G;A)$ remains basically unknown. In particular, the study of $\mathrm {CA}(G;A)$, when G and A are both finite, has been generally disregarded, perhaps because some of the classical questions are trivially answered (e.g. the Garden of Eden theorems become trivial). However, many new questions, typical of finite semigroup theory, arise in this setting.

In this paper, we study various algebraic properties of $\mathrm {CA}(G;A)$ when G and A are both finite. First, in Sect. 2, we introduce notation and review some basic results. In Sect. 3, we study the group $\mathrm {ICA}(G;A)$ consisting of all invertible CA: we show that its structure is linked with the number of conjugacy classes of subgroups of G, and we give an explicit decomposition in terms of direct and wreath products.

In Sect. 4, we study generating sets of $\mathrm {CA}(G;A)$. We prove that $\mathrm {CA}(G;A)$ cannot be generated by CA with small memory sets: if T generates $\mathrm {CA}(G;A)$, then T must contain a cellular automaton with minimal memory set equal to G itself. This result provides a striking contrast with CA over infinite groups. Finally, when G is finite abelian, we find the smallest size of a set $U \subseteq \mathrm {CA}(G;A)$ such that $\mathrm {ICA}(G;A) \cup U$ generate $\mathrm {CA}(G;A)$; this number is known in semigroup theory as the relative rank of $\mathrm {ICA}(G;A)$ in $\mathrm {CA}(G;A)$, and it turns out to be related with the number of edges of the subgroup lattice of G.

2 Basic Results

For any set X, let $\mathrm {Tran}(X)$ and $\mathrm {Sym}(X)$ be the sets of all functions and bijective functions, respectively, of the form $\tau : X \rightarrow X$. Equipped with the composition of functions, $\mathrm {Tran}(X)$ is known as the full transformation monoid on X, while $\mathrm {Sym}(X)$ is the symmetric group on X. When X is finite and $\vert X \vert = q$, we write $\mathrm {Tran}_q$ and $\mathrm {Sym}_q$ instead of $\mathrm {Tran}(X)$ and $\mathrm {Sym}(X)$, respectively.

A finite transformation monoid is simply a submonoid of $\mathrm {Tran}_q$, for some q. This type of monoids has been extensively studied (e.g. see [6] and references therein), and it should be noted its close relation to finite-state machines.

For the rest of the paper, let G be a finite group of size n and A a finite set of size q. By Definition 1, it is clear that $\mathrm {CA}(G;A) \le \mathrm {Tran}(A^G)$ (we use the symbol “$\le$” for the submonoid relation). We may always assume that $\tau \in \mathrm {CA}(G;A)$ has (not necessarily minimal) memory set $S = G$, so $\tau$ is completely determined by its local function $\mu : A^G \rightarrow A$. Hence, $\vert \mathrm {CA}(G ; A) \vert = q^{q^n}$.

If $n=1$, then $\mathrm {CA}(G;A) = \mathrm {Tran}(A)$, while, if $q \le 1$, then $\mathrm {CA}(G;A)$ is the trivial monoid with one element; henceforth, we assume $n \ge 2$ and $q \ge 2$. We usually identify A with the set $\{0, 1, \dots , q-1 \}$.

The group G acts on the configuration space $A^G$ as follows: for each $g \in G$ and $x \in A^G$, the configuration $x \cdot g \in A^G$ is defined by

$$\begin{aligned} (h)x \cdot g = (hg^{-1})x, \quad \forall h \in G. \end{aligned}$$

A transformation $\tau : A^G \rightarrow A^G$ is G-equivariant if, for all $x \in A^G$, $g \in G$,

$$\begin{aligned} (x \cdot g) \tau = ( (x) \tau ) \cdot g . \end{aligned}$$

Denote by $\mathrm {ICA}(G;A)$ the group of all invertible cellular automata:

$$\begin{aligned} \mathrm {ICA}(G;A) := \{ \tau \in \mathrm {CA}(G;A) : \exists \phi \in \mathrm {CA}(G;A) \text { such that } \tau \phi = \phi \tau = \mathrm {id}\}. \end{aligned}$$

Theorem 1

Let G be a finite group and A a finite set.

• (i) $\mathrm {CA}(G;A) = \{ \tau \in \mathrm {Tran}(A^G) : \tau \text { is G-equivariant} \}$.

• (ii) $\mathrm {ICA}(G;A) = \mathrm {CA}(G;A) \cap \mathrm {Sym}(A^G)$.

Proof

The first part follows by Curtis-Hedlund Theorem (see [4, Theorem 1.8.1]) while the second part follows by [4, Theorem 1.10.2].    $\square$

Notation 1

For any $x \in A^G$, denote by xG the G-orbit of x on $A^G$:

$$\begin{aligned} xG := \{ x \cdot g : g \in G \}. \end{aligned}$$

Let $\mathcal {O}(G;A)$ be the set of all G-orbits on $A^G$:

$$\begin{aligned} \mathcal {O}(G;A) := \{ xG : x \in A^G\}. \end{aligned}$$

Clearly, $\mathcal {O}(G;A)$ forms a partition of $A^G$. In general, when X is a set and $\mathcal {P}$ is a partition of X, we say that a transformation monoid $M \le \mathrm {Tran}(X)$ preserves the partition if, for any $P \in \mathcal {P}$ and $\tau \in M$ there is $Q \in \mathcal {P}$ such that $(P)\tau \subseteq Q$.

Lemma 1

For any $x \in A^G$ and $\tau \in \mathrm {CA}(G;A)$,

$$\begin{aligned} (xG) \tau = (x)\tau G. \end{aligned}$$

In particular, $\mathrm {CA}(G;A)$ preserves the partition $\mathcal {O}(G;A)$ of $A^G$.

Proof

The result follows by the G-equivariance of $\tau \in \mathrm {CA}(G;A)$.    $\square$

A configuration $x \in A^G$ is called constant if $(g)x = k \in A$, for all $g \in G$. In such case, we usually denote x by $\mathbf {k} \in A^G$.

Lemma 2

Let $\tau \in \mathrm {CA}(G;A)$ and let $\mathbf {k} \in A^G$ be a constant configuration. Then, $(\mathbf {k}) \tau \in A^G$ is a constant configuration.

Proof

Observe that $x \in A^G$ is constant if and only if $x \cdot g = x$, for all $g \in G$. By G-equivariance,

$$\begin{aligned} (\mathbf {k}) \tau = (\mathbf {k} \cdot g) \tau = (\mathbf {k}) \tau \cdot g, \quad \forall g \in G. \end{aligned}$$

Hence, $(\mathbf {k})\tau$ is constant.    $\square$

For a monoid M and a subset $T \subseteq M$, denote by $C_M(T)$ the centraliser of T in M:

$$\begin{aligned} C_M(T) := \{ m \in M : mt=tm, \forall t \in T \}. \end{aligned}$$

If G is abelian, the transformation $\sigma _g : A^G \rightarrow A^G$, with $g \in G$, defined by

$$\begin{aligned} (x) \sigma _g := x\cdot g , \quad \forall x \in A^G, \end{aligned}$$

is in $\mathrm {CA}(G;A)$. It follows by Theorem 1 that $CA(G;A) = C_{\mathrm {Tran}(A^G)}(T)$, where $T :=\{ \sigma _g : g \in G \}$.

We use the cyclic notation for the permutations of $\mathrm {Sym}(A^G)$. If $B \subseteq A^G$ and $a \in A^G$, we define the idempotent transformation $(B \rightarrow a) \in \mathrm {Tran}(A^G)$ by

$$ (x)(B \rightarrow a) := {\left\{ \begin{array}{ll} a &{} \text { if } x \in B, \\ x &{} \text { otherwise}, \end{array}\right. } \quad \forall x \in A^G. $$

When $B=\{ b\}$ is a singleton, we write $(b \rightarrow a)$ instead of $(\{ b\} \rightarrow a)$.

3 The Structure of $\mathrm {ICA}(G;A)$

Let G be a finite group of size $n \ge 2$ and A a finite set of size $q \ge 2$. We review few basic concepts about permutation groups (see [5, Ch.1]). For $x \in A^G$, denote by $G_x$ the stabiliser of x in G:

$$\begin{aligned} G_x : = \{g \in G : x \cdot g = x \}. \end{aligned}$$

Remark 1

For any subgroup $H \le G$ there exists $x \in A^G$ such that $G_x = H$; namely, we may define $x : G \rightarrow A$ by

$$ (g)x := {\left\{ \begin{array}{ll} 1 &{} \text {if } g \in H, \\ 0 &{} \text {otherwise}, \end{array}\right. } \quad \forall g \in G. $$

Say that two subgroups $H_1$ and $H_2$ of G are conjugate in G if there exists $g \in G$ such that $g^{-1} H_1 g = H_2$. This defines an equivalence relation on the subgroups of G. Denote by [H] the conjugacy class of $H \le G$.

We say that the actions of G on two sets $\varOmega$ and $\varGamma$ are equivalent if there is a bijection $\lambda : \varOmega \rightarrow \varGamma$ such that, for all $x \in \varOmega , g \in G$, we have $(x \cdot g )\lambda = (x)\lambda \cdot g$.

The following is an essential result for our description of the structure of the group of invertible cellular automata.

Lemma 3

Let G be a finite group of size $n \ge 2$ and A a finite set of size $q \ge 2$. For any $x,y \in A^G$, there exists $\tau \in \mathrm {ICA}(G;A)$ such that $(xG)\tau = yG$ if and only if $[G_x] = [ G_y]$.

Proof

By [5, Lemma 1.6B], the actions of G on xG and yG are equivalent if and only if $G_x$ and $G_y$ are conjugate in G. We claim that the actions of G on xG and yG are equivalent if and only if there is $\tau \in \mathrm {ICA}(G;A)$ such that $(xG) \tau = yG$. Assume such $\tau \in \mathrm {ICA}(G;A)$ exists. Then, the restriction $\lambda := \tau \vert _{xG} : xG \rightarrow yG$ is the bijection required to show that the actions of G on xG and yG are equivalent. Conversely, suppose there is a bijection $\lambda : xG \rightarrow yG$ such that $(z \cdot g )\lambda = (z)\lambda \cdot g$, for all $z \in xG$, $g \in G$. Define $\tau : A^G \rightarrow A^G$ by

$$ (z)\tau := {\left\{ \begin{array}{ll} (z)\lambda &{} \text {if } z \in xG, \\ (z)\lambda ^{-1} &{} \text {if } z \in yG, \\ z &{} \text {otherwise}, \end{array}\right. } \quad \forall z \in A^G. $$

Clearly, $\tau$ is G-equivariant and invertible (in fact, $\tau = \tau ^{-1}$). Hence $\tau \in \mathrm {ICA}(G;A)$, and it satisfies $(xG)\tau = yG$.    $\square$

Corollary 1

Suppose that G is a finite abelian group. For any $x,y \in A^G$, there exists $\tau \in \mathrm {ICA}(G;A)$ such that $(xG)\tau = yG$ if and only if $G_x = G_y$.

For any integer $\alpha \ge 2$ and any group C, the wreath product of C by $\mathrm {Sym}_\alpha$ is the set

$$\begin{aligned} C \wr \mathrm {Sym}_{\alpha } := \{ (v; \phi ) : v \in C ^\alpha , \phi \in \mathrm {Sym}_\alpha \} \end{aligned}$$

equipped with the operation

$$\begin{aligned} (v;\phi ) \cdot (w; \psi ) = ( v w^{\phi }; \phi \psi ), \text { for any } v,w \in C^\alpha , \phi , \psi \in \mathrm {Sym}_\alpha , \end{aligned}$$

where $\phi$ acts on w by permuting its coordinates:

$$\begin{aligned} w^\phi = (w_1, w_2, \dots , w_\alpha )^\phi := (w_{(1)\phi }, w_{(2)\phi }, \dots , w_{(\alpha )\phi }). \end{aligned}$$

See [5, Sect. 2.6] for a more detailed description of the wreath product.

Notation 2

Let $O \in \mathcal {O}(G;A)$ be a G-orbit. If $G_{(O)}$ is the pointwise stabiliser of O, i.e. $G_{(O)} := \bigcap _{x \in O} G_x$, the group $G^O := G / G_{(O)}$ is isomorphic to a subgroup of $\mathrm {Sym}(O)$ (see [5, p. 17]). Abusing the notation, we also write $G^O$ for the isomorphic copy of $G^O$ inside $\mathrm {Sym}(O)$. Define the group

$$\begin{aligned} C(G^O) := \{ \tau \vert _{O} : O \rightarrow A^G : \tau \in \mathrm {ICA}(G;A) \text { and } (O)\tau = O \}. \end{aligned}$$

(1)

By Theorem 1, $C(G^O)$ is isomorphic to the centraliser of $G^O$ in $\mathrm {Sym}(O)$, i.e. $C(G^O) \cong C_{\mathrm {Sym}(O)}(G^O)$.

Notation 3

Let H be a subgroup of G and [H] its conjugacy class. Define

$$\begin{aligned} B_{[H]} := \{ x \in A^G : G_x \in [H] \}. \end{aligned}$$

Note that $B_{[H]}$ is a union of G-orbits and, by the Orbit-Stabiliser Theorem (see [5, Theorem 1.4A]), all the G-orbits contained in $B_{[H]}$ have equal sizes. Define

$$\begin{aligned} \alpha _{[H]} (G; A) := \left| \left\{ O \in \mathcal {O}(G,A) : O \subseteq B_{[H]} \right\} \right| . \end{aligned}$$

If r is the number of different conjugacy classes of subgroups of G, observe that

$$\begin{aligned} \mathcal {B} := \{ B_{[H]} : H \le G \} \end{aligned}$$

is a partition of $A^G$ with r blocks.

Remark 2

  $B_{[G]} = \{ x \in A^G : x \text { is constant} \}$ and $\alpha _{[G]} (G; A) = q$.

Example 1

Let $G = \mathbb {Z}_2 \times \mathbb {Z}_2$ be the Klein four-group and $A= \{ 0, 1\}$. As G is abelian, $[H] = \{ H\}$, for all $H \le G$. The subgroups of G are

$$\begin{aligned} H_1 = G, \ H_2 = \langle (1,0) \rangle , \ H_3 = \langle (0,1) \rangle , \ H_4 = \langle (1,1) \rangle , \ \text {and} \ H_5 = \langle (0,0) \rangle , \end{aligned}$$

where $\langle (a,b) \rangle$ denotes the subgroup generated by $(a,b) \in G$. Any configuration $x : G \rightarrow A$ may be written as a $2 \times 2$ matrix $(x_{i,j})$ where $x_{i,j} := (i-1,j-1)x$, $i,j \in \{1,2 \}$. The G-orbits on $A^G$ are

Hence,

$$\begin{aligned}&B_{[H_1]}:=O_1 \cup O_2, \ B_{[H_2]}:=O_3, \ B_{[H_3]}:=O_4, \ B_{[H_4]}:=O_5, \ B_{[H_5]}:=O_6 \cup O_7; \\&\alpha _{[H_i]}(G;A) = 2, \text{ for } i \in \{1,5 \}, \text{ and } \alpha _{[H_i]}(G;A) = 1, \text { for } i \in \{ 2,3,4 \}. \end{aligned}$$

Remark 3

By Lemma 3, the $\mathrm {ICA}(G;A)$-orbits on $A^G$ coincide with the blocks in $\mathcal {B}$, while the $\mathrm {ICA}(G;A)$-blocks of imprimitivity on each $B_{[H]}$ are the G-orbits contained in $B_{[H]}$.

The following result is a refinement of [12, Theorem 9] and [3, Lemma 4].

Theorem 2

Let G be a finite group and A a finite set of size $q \ge 2$. Let $[H_1], \dots , [H_r]$ be the list of different conjugacy classes of subgroups of G. For each $1 \le i \le r$, fix a G-orbit $O_i \subseteq B_{[H_i]}$. Then,

$$\begin{aligned} \mathrm {ICA}(G;A) \cong \prod _{i=1}^r \left( C_i \wr \mathrm {Sym}_{\alpha _i} \right) , \end{aligned}$$

where $C_i := C(G^{O_i}) \cong C_{\mathrm {Sym}(O_i)}(G^{O_i})$ and $\alpha _i := \alpha _{[H_i]}(G;A)$.

Proof

Let $B_i := B_{[H_i]}$. By Lemma 3, $\mathrm {ICA}(G;A)$ is contained in the group

$$\begin{aligned} \prod _{i=1}^r \mathrm {Sym}(B_i) = \mathrm {Sym}(B_1) \times \mathrm {Sym}(B_2) \times \dots \times \mathrm {Sym}(B_r). \end{aligned}$$

For each $1 \le i \le r$, let $\mathcal {O}_i$ be the set of G-orbits contained in $B_i$ (so $O_i \in \mathcal {O}_i$). Note that $\mathcal {O}_i$ is a uniform partition of $B_i$. For any $\tau \in \mathrm {ICA}(G;A)$, Lemma 1 implies that the projection of $\tau$ to $\mathrm {Sym}(B_i)$ is contained in

$$\begin{aligned} S(B_i, \mathcal {O}_i ) := \{ \phi \in \mathrm {Sym}(B_i) : \forall P \in \mathcal {O}_i, \ (P)\phi \in \mathcal {O}_i \}. \end{aligned}$$

By [2, Lemma 2.1(iv)],

$$\begin{aligned} S(B_i , \mathcal {O}_i ) \cong \mathrm {Sym}(O_i) \wr \mathrm {Sym}_{\alpha _i}. \end{aligned}$$

It is well-known that $\mathrm {Sym}_{\alpha _i}$ is generated by its transpositions. As the invertible cellular automaton constructed in the proof of Lemma 3 induces a transposition $(xG,yG) \in \mathrm {Sym}_{\alpha _i}$, with $xG, yG \in \mathcal {O}_i$, we deduce that $\mathrm {Sym}_{\alpha _i} \le \mathrm {ICA}(G;A)$. The result follows by the construction of $C_i \cong C_{\mathrm {Sym}(O_i)}(G^{O_i})$ and Theorem 1.    $\square$

Corollary 2

Let G be a finite abelian group and A a finite set of size $q\ge 2$. Let $H_1, \dots , H_r$ be the list of different subgroups of G. Then,

$$\begin{aligned} \mathrm {ICA}(G;A) \cong \prod _{i=1}^r \left( (G/H_i) \wr \mathrm {Sym}_{\alpha _i} \right) , \end{aligned}$$

and $\vert G \vert \alpha _i = \vert H_i \vert \cdot \vert \{ x \in A^G : G_x = H_i \} \vert$, where $\alpha _i := \alpha _{[H_i]}(G;A)$.

Proof

By [5, Theorem 4.2A(v)], $C_{\mathrm {Sym}(O_i)}(G^{O_i}) \cong G^{O_i} \cong G/G_{x_i}$, where $x_i \in O_i$. By Remark 1, the list of pointwise stabilisers coincide with the list of subgroups of G, and, as G is abelian, $[H_i] = \{ H_i \}$ for all i. Finally, by the Orbit-Stabiliser theorem, every orbit contained in $B_i = \{ x \in A^G : G_x = H_i \}$ has size $\frac{\vert G \vert }{\vert H_i \vert }$; as these orbits form a partition of $B_i$, we have $\vert B_i \vert = \alpha _i \frac{\vert G \vert }{\vert H_i \vert }$.    $\square$

Example 2

Let $G = \mathbb {Z}_2 \times \mathbb {Z}_2$ and $A= \{ 0, 1\}$. By Example 1,

$$\begin{aligned} \mathrm {ICA}(G, A ) \cong (\mathbb {Z}_2)^4 \times (G \wr \mathrm {Sym}_2). \end{aligned}$$

4 Generating Sets of of $\mathrm {CA}(G;A)$

For a monoid M and a subset $T \subseteq M$, denote by $\langle T \rangle$ the submonoid generated by T, i.e. the smallest submonoid of M containing T. Say that T is a generating set of M if $M = \langle T \rangle$; in this case, every element of M is expressible as a word in the elements of T (we use the convention that the empty word is the identity).

Define the kernel of a transformation $\tau : X \rightarrow X$, denoted by $\ker (\tau )$, as set of the equivalence classes on X of the equivalence relation $\{ (x,y ) \in X^2 : (x)\tau = (y) \tau \}$. For example, $\ker (\phi ) = \{ \{ x\} : x \in X\}$, for any $\phi \in \mathrm {Sym}(X)$, while $\ker (y \rightarrow z) = \{ \{ y, z \}, \{x \} : x \in X \setminus \{ y,z\} \}$, for $y, z \in X$, $y \ne z$.

A large part of the classical research on CA has been focused on CA with small memory sets. In some cases, such as the elementary Rule 110, or John Conway’s Game of Life, these CA are known to be Turing complete. In a striking contrast, when G and A are both finite, CA with small memory sets are insufficient to generate the monoid $\mathrm {CA}(G;A)$.

Theorem 3

Let G be a finite group of size $n \ge 2$ and A a finite set of size $q \ge 2$. Let T be a generating set of $\mathrm {CA}(G;A)$. Then, there exists $\tau \in T$ with minimal memory set $S=G$.

Proof

Suppose that T is a generating set of $\mathrm {CA}(G, A)$ such that each of its elements has minimal memory set of size at most $n-1$. Consider the idempotent $\sigma :=(\mathbf {0} \rightarrow \mathbf {1}) \in \mathrm {CA}(G, A)$, where $\mathbf 0 , \mathbf 1 \in A^G$ are different constant configurations. Then, $\sigma = \tau _1 \tau _2 \dots \tau _\ell$, for some $\tau _i \in T$. By the definition of $\sigma$ and Lemma 2, there must be $1 \le j \le \ell$ such that $\left| ( A^G_{\text {c}})\tau _j \right| = q-1$ and $( A^G_{\text {nc}})\tau _j = A^G_{\text {nc}}$, where

$$\begin{aligned} A^G_{\text {c}}:= \{ \mathbf {k} \in A^G : \mathbf {k} \text { is constant} \} \text { and } A^G_{\text {nc}} := \{ x \in A^G : x \text { is non-constant} \}. \end{aligned}$$

Let $S \subseteq G$ and $\mu : A^S \rightarrow A$ be the minimal memory set and local function of $\tau := \tau _j$, respectively. By hypothesis, $s := \vert S \vert < n$. Since the restriction of $\tau$ to $A^G_{\text {c}}$ is not a bijection, there exists $\mathbf {k} \in A^G_{\text {c}}$ (defined by $(g)\mathbf {k}:=k \in A$, $\forall g \in G$) such that $\mathbf {k} \not \in ( A^G_{\text {c}})\tau$.

For any $x \in A^G$, define the k-weight of x by

$$\begin{aligned} \vert x \vert _k := \vert \{ g \in G : (g)x \ne k \} \vert . \end{aligned}$$

Consider the sum of the k-weights of all non-constant configurations of $A^G$:

$$\begin{aligned} w := \sum _{x \in A^G_{\text {nc}} } \vert x \vert _k = n(q-1) q^{n-1} - n(q-1) = n(q-1) ( q^{n-1} - 1) . \end{aligned}$$

In particular, $\frac{w}{n}$ is an integer not divisible by q.

For any $x \in A^G$ and $y \in A^S$, define

$$\begin{aligned} \mathrm {Sub}(y, x) := \vert \{ g \in G : y = x \vert _{Sg} \} \vert ; \end{aligned}$$

this counts the number of times that y appears as a subconfiguration of x. Then, for any fixed $y \in A^S$,

$$ N_y := \sum _{x \in A^G_{\text {nc}}} \mathrm {Sub}(y,x) = {\left\{ \begin{array}{ll} n q^{n-s}&{} \text {if } y \in A^S_{\text {nc}}, \\ n (q^{n-s} - 1 )&{} \text {if } y \in A^S_{\text {c}}. \end{array}\right. } $$

Let $\delta : A^2 \rightarrow \{0,1 \}$ be the Kronecker’s delta function. Since $( A^G_{\text {nc}})\tau = A^G_{\text {nc}}$, we have

$$\begin{aligned} w&= \sum _{x \in A^G_{\text {nc}} } \vert (x)\tau \vert _k = \sum _{y \in A^S} N_y ( 1 - \delta ( (y)\mu , k) ) \\&= n q^{n-s} \sum _{y \in A^S_{\text {nc}}} ( 1 - \delta ( (y)\mu , k) ) + n ( q^{n-s} - 1 ) \sum _{y \in A^S_{\text {c}}} ( 1 - \delta ( (y)\mu , k) ). \end{aligned}$$

Because $\mathbf {k} \not \in ( A^G_{\text {c}})\tau$, we know that $(y)\mu \ne k$ for all $y \in A^S_{\text {c}}$. Therefore,

$$\begin{aligned} \frac{w}{n} = q^{n-s} \sum _{y \in A^S_{\text {nc}}} ( 1 - \delta _{ (y)\mu , k} ) + ( q^{n-s} - 1 ) q. \end{aligned}$$

As $s <n$, this implies that $\frac{w}{n}$ is an integer divisible by q, which is a contradiction.   $\square$

One of the fundamental problems in the study of a finite monoid M is the determination of the cardinality of a smallest generating subset of M; this is called the rank of M and denoted by $\mathrm {Rank}(M)$:

$$\begin{aligned} \mathrm {Rank}(M) := \min \{ \vert T \vert : T \subseteq M \text { and } \langle T \rangle = M \}. \end{aligned}$$

It is well-known that, if X is any finite set, the rank of the full transformation monoid $\mathrm {Tran}(X)$ is 3, while the rank of the symmetric group $\mathrm {Sym}(X)$ is 2 (see [6, Ch. 3]). Ranks of various finite monoids have been determined in the literature before (e.g. see [1, 2, 7, 8, 10]).

In [3], the rank of $\mathrm {CA}(\mathbb {Z}_n, A)$, where $\mathbb {Z}_n$ is the cyclic group of order n, was studied and determined when $n \in \{ p, 2^k, 2^k p : k \ge 1, \ p \text { odd prime} \}$. Moreover, the following problem was proposed:

Problem 1

For any finite group G and finite set A, determine $\mathrm {Rank}(\mathrm {CA}(G;A))$.

For any finite monoid M and $U \subseteq M$, the relative rank of U in M, denoted by $\mathrm {Rank}(M:U)$, is the minimum cardinality of a subset $V \subseteq M$ such that $\langle U \cup V \rangle = M$. For example, for any finite set X,

$$\begin{aligned} \mathrm {Rank}(\mathrm {Tran}(X): \mathrm {Sym}(X)) = 1, \end{aligned}$$

as any $\tau \in \mathrm {Tran}(X)$ with $\vert (X) \tau \vert = \vert X \vert -1$ satisfies $\langle \mathrm {Sym}(X) \cup \{ \tau \} \rangle = \mathrm {Tran}(X)$. One of the main tools that may be used to determine $\mathrm {Rank}(\mathrm {CA}(G;A))$ is based on the following result (see [2, Lemma 3.1]).

Lemma 4

Let G be a finite group and A a finite set. Then,

$$\begin{aligned} \mathrm {Rank}(\mathrm {CA}(G ; A)) = \mathrm {Rank}(\mathrm {CA}(G;A):\mathrm {ICA}(G;A)) + \mathrm {Rank}(\mathrm {ICA}(G;A)). \end{aligned}$$

We shall determine the relative rank of $\mathrm {ICA}(G;A)$ in $\mathrm {CA}(G;A)$ for any finite abelian group G and finite set A. In order to achieve this, we prove two lemmas that hold even when G is nonabelian and have relevance in their own right.

Lemma 5

Let G be a finite group and A a finite set of size $q\ge 2$. Let $x\in A^G$. If $(x)\tau \in xG$, then $\tau \vert _{xG} \in \mathrm {Sym}(xG)$.

Proof

It is enough to show that $(xG)\tau = xG$ as this implies that $\tau \vert _{xG} : xG \rightarrow xG$ is surjective, so it is bijective by the finiteness of xG. Since $(x)\tau \in xG$, we know that $(x)\tau G = xG$. Hence, by Lemma 1,

$$ (xG)\tau = (x) \tau G = x G. $$

   $\square$

Notation 4

Denote by $\mathcal {C}_G$ the set of conjugacy classes of subgroups of G. For any $[H_1], [H_2] \in \mathcal {C}_G$, write $[H_1] \le [H_2]$ if $H_1 \le g^{-1} H_2 g$, for some $g \in G$.

Remark 4

The relation $\le$ defined above is a well-defined partial order on $\mathcal {C}_G$. Clearly, $\le$ is reflexive and transitive. In order to show antisymmetry, suppose that $[H_1] \le [H_2]$ and $[H_2] \le [H_1]$. Then, $H_1 \le g^{-1} H_2 g$ and $H_2 \le f^{-1} H_1 f$, for some $f,g \in G$, which implies that $\vert H_1 \vert \le \vert H_2 \vert$ and $\vert H_2 \vert \le \vert H_1 \vert$. As $H_1$ and $H_2$ are finite, $\vert H_1 \vert = \vert H_2 \vert$, and $H_1 = g^{-1} H_2 g$. This shows that $[H_1] = [H_2]$.

Lemma 6

Let G be a finite group and A a finite set of size $q\ge 2$. Let $x , y \in A^G$ be such that $xG \ne yG$. There exists a non-invertible $\tau \in \mathrm {CA}(G;A)$ such that $(xG)\tau = yG$ if and only if $[G_x] \le [G_y]$.

Proof

Suppose that $[G_x] \le [G_y]$. Then, $G_x \le g^{-1} G_y g$, for some $g \in G$. We define an idempotent $\tau _{x,y} : A^G \rightarrow A^G$ that maps xG to yG:

$$ (z) \tau _{x,y} := {\left\{ \begin{array}{ll} y \cdot g h &{} \text {if } z = x \cdot h, \\ z &{} \text {otherwise}, \end{array}\right. } \quad \forall z \in A^G. $$

We verify that $\tau _{x,y}$ is well-defined. If $x \cdot h_1 = x \cdot h_2$, for $h_i \in G$, then $h_1 h_2^{-1} \in G_x$. As $G_x \le g^{-1} G_y g$, we have $h_1 h_2^{-1} = g^{-1} s g$, for some $s \in G_y$. Thus, $g h_1 = s g h_2$ implies that $y \cdot gh_1 = y \cdot g h_2$, and $(x \cdot h_1 )\tau _{x,y} = (x \cdot h_2) \tau _{x,y}$. Clearly, $\tau _{x,y}$ is non-invertible and G-equivariant, so $\tau _{x,y}\in \mathrm {CA}(G;A)$.

Conversely, suppose there exists $\tau \in \mathrm {CA}(G;A)$ such that $(xG)\tau = yG$. Then, $(x)\tau = y \cdot h$, for some $h \in G$. Let $s \in G_x$. By G-equivariance,

$$\begin{aligned} y\cdot h = (x) \tau = (x \cdot s) \tau = (x) \tau \cdot s = y \cdot hs . \end{aligned}$$

Thus $h s h^{-1} \in G_y$ and $s \in h^{-1} G_y h$. This shows that $[G_x] \le [G_y]$.    $\square$

Corollary 3

Suppose that G is finite abelian. Let $x,y \in A^G$ be such that $xG \ne yG$. There exists $\tau _{x,y} \in \mathrm {CA}(G;A)$ such that $(x)\tau _{x,y} = y$ and $(z)\tau _{x,y} = z$ for all $z \in A^G \setminus xG$ if and only if $G_x \le G_y$.

Notation 5

Consider the directed graph $(\mathcal {C}_G, \mathcal {E}_G)$ with vertex set $\mathcal {C}_G$ and edge set

$$ \mathcal {E}_G := \left\{ ([H_i], [H_j]) \in \mathcal {C}_G^2 : [H_i] \le [H_j] \right\} . $$

When G is abelian, this graph coincides with the lattice of subgroups of G.

Remark 5

Lemma 6 may be restated in terms of $\mathcal {E}_G$. By Lemma 5, loops $([H_i],[H_i])$ do not have corresponding non-invertible CA when $\alpha _{[H_i]}(G;A)=1$.

Theorem 4

Let G be a finite abelian group and A a finite set of size $q\ge 2$. Let $H_1, H_2, \dots , H_r$ be the list of different subgroups of G with $H_1 = G$. For each $1 \le i \le r$, let $\alpha _i := \alpha _{[H_i]}(G;A)$. Then,

$$\begin{aligned} \mathrm {Rank}(\mathrm {CA}(G;A):\mathrm {ICA}(G;A)) = \vert \mathcal {E}_G \vert - \sum _{i=2}^r \delta (\alpha _i,1), \end{aligned}$$

where $\delta : \mathbb {N}^2 \rightarrow \{0,1 \}$ is Kronecker’s delta function.

Proof

For all $1 \le i \le r$, let $B_i := B_{[H_i]}$. Fix orbits $x_i G \subseteq B_i$, so $H_i = G_{x_i}$. Assume that the list of subgroups of G is ordered such that

$$\begin{aligned} \vert x_1 G \vert \le \dots \le \vert x_r G \vert , \text { or, equivalently, } \vert G_{x_1} \vert \ge \dots \ge \vert G_{x_r} \vert . \end{aligned}$$

For every $\alpha _i \ge 2$, fix orbits $y_i G \subseteq B_i$ such that $x_i G \ne y_i G$. We claim that $\mathrm {CA}(G,A) = M:= \left\langle \mathrm {ICA}(G;A) \cup U \right\rangle$, where

$$\begin{aligned} U := \left\{ \tau _{x_i,x_j} : [G_{x_i}] < [G_{x_j}] \right\} \cup \left\{ \tau _{x_i, y_i} : \alpha _i \ge 2 \right\} , \end{aligned}$$

and $\tau _{x_i, x_j}, \tau _{x_i, y_i}$ are the idempotents defined in Corollary 3. For any $\tau \in \mathrm {CA}(G;A)$, consider $\tau _i \in \mathrm {CA}(G;A)$, $1 \le i \le r$, defined by

$$ (x)\tau _i = {\left\{ \begin{array}{ll} (x)\tau &{} \text {if } x \in B_i \\ x &{} \text {otheriwse}. \end{array}\right. }$$

By Lemmas 3 and 6, $(B_i)\tau \subseteq \bigcup _{j \le i} B_j$ for all i. Hence, we have the decomposition

$$\begin{aligned} \tau = \tau _1 \tau _2 \dots \tau _r. \end{aligned}$$

We shall prove that $\tau _i \in M$ for all $1 \le i \le r$. For each i, decompose $B_i = B_i^{\prime } \cup B_i^{\prime \prime }$, where

$$\begin{aligned} B_i^\prime&:= \bigcup \left\{ P \in \mathcal {O}(G;A) : P \subseteq B_i \text { and } (P)\tau _i \subseteq B_j \text { for some } j <i \right\} , \\ B_i^{\prime \prime }&:= \bigcup \left\{ P \in \mathcal {O}(G;A) : P \subseteq B_i \text { and } (P)\tau _i \subseteq B_i \right\} . \end{aligned}$$

If $\tau ^\prime _i$ and $\tau ^{\prime \prime }_i$ are the transformations that act as $\tau _i$ on $B_i^\prime$ and $B_i^{\prime \prime }$, respectively, and fix everything else, then $\tau _i = \tau _i^{\prime } \tau _{i}^{\prime \prime }$. We shall prove that $\tau _i^\prime \in M$ and $\tau _i^{\prime \prime } \in M$.

• 1. We show that $\tau _i^{\prime } \in M$. For any orbit $P \in B_i^\prime$, the orbit $Q:= (P)\tau _{i}^{\prime }$ is contained in $B_j$ for some $j < i$. By Theorem 2, there exist

  $$\begin{aligned} \phi \in \left( (G/ G_{x_i}) \wr \mathrm {Sym}_{\alpha _i} \right) \times \left( (G/ G_{x_j}) \wr \mathrm {Sym}_{\alpha _j} \right) \le \mathrm {ICA}(G;A) \end{aligned}$$

  such that $\phi$ acts as the double transposition $(x_i G, P) (x_j G, Q)$. Since $G/ G_{x_i}$ and $G/ G_{x_j}$ are transitive on $x_i G$ and $x_j G$, respectively, we may take $\phi$ such that $(x_i) \phi \tau _i^\prime = (x_j) \phi$. Then,

  $$\begin{aligned} (z) \tau _i^\prime = (z) \phi \tau _{x_i, x_j} \phi , \ \forall z \in P. \end{aligned}$$

  As $\tau _i^\prime$ may be decomposed as a product of transformations that only move one orbit in $B_i^{\prime }$, this shows that $\tau _i^\prime \in M$.

• 2. We show that $\tau _{i}^{\prime \prime } \in M$. In this case, $\tau _i^{\prime \prime } \in \mathrm {Tran}(B_i)$. In fact, as $\tau _i^{\prime \prime }$ preserves the partition of $B_i$ into G-orbits, Lemma 5 implies that $\tau _i^{\prime \prime } \in (G/G_{x_i}) \wr \mathrm {Tran}_{\alpha _i}$. If $\alpha _i \ge 2$, the semigroup $\mathrm {Tran}_{\alpha _i}$ is generated by $\mathrm {Sym}_{\alpha _i} \le \mathrm {ICA}(G,A)$ together with the idempotent $\tau _{x_i, y_i}$. Hence, $\tau _i^{\prime \prime } \in M$.

Therefore, we have established that $\mathrm {CA}(G;A) = \left\langle \mathrm {ICA}(G;A) \cup U \right\rangle$.

Suppose now that there exists $V \subseteq \mathrm {CA}(G;A)$ such that $\vert V \vert < \vert U \vert$ and

$$\begin{aligned} \left\langle \mathrm {ICA}(G ; A) \cup V \right\rangle = \mathrm {CA}(G ; A). \end{aligned}$$

The elements of U have all different kernels, so, for some $\tau \in U$, we must have

$$\begin{aligned} V \cap \langle \mathrm {ICA}(G; A) , \tau \rangle = \emptyset . \end{aligned}$$

(Otherwise, V has at least $\vert U \vert$ transformations with different kernels, which is impossible since $\vert V \vert < \vert U \vert$). If $\tau = \tau _{x_i,y_i}$, for some i with $\alpha _i \ge 2$, this implies that there is no $\xi \in V$ with

$$\begin{aligned} \ker (\xi ) = \left\{ \{a, b \}, \{ c \} : a \in x_i G, \ b \in y_i G, \ c \in A^G \setminus (x_iG \cup y_i G) \right\} . \end{aligned}$$

Hence, there is no $\xi \in \left\langle \mathrm {ICA}(G ; A) \cup V \right\rangle = \mathrm {CA}(G ; A)$ with kernel of this form, which is a contradiction because $\tau _{x_i,y_i}$ itself has kernel of this form. We obtain a similar contradiction if $\tau = \tau _{x_i,x_j}$ with $[G_{x_i}] < [G_{x_j}]$.    $\square$

Corollary 4

Let G be a finite abelian group with $\mathrm {Rank}(G) = m$ and A a finite set of size $q \ge 2$. With the notation of Theorem 4,

$$\begin{aligned} \mathrm {Rank}(\mathrm {CA}(G;A))&\le \sum _{i=2}^r m \alpha _i + 2 r + \vert \mathcal {E}_G \vert - \delta (q,2) - \sum _{i=2}^r ( 3\delta (\alpha _i,1) + \delta (\alpha _i,2) ) \\&\le \sum _{i=2}^r m \alpha _i + 2r + r^2. \end{aligned}$$

Proof

Using the fact $\mathrm {Rank}((G/H_i)\wr \mathrm {Sym}_{\alpha _i}) \le m \alpha _i + 2 - 2\delta (\alpha _i,1) - \delta (\alpha _i,2)$ and $\mathrm {Rank}((G/H_1)\wr \mathrm {Sym}_{q}) = 2 - \delta (q,2)$, the result follows by Theorem 4, Corollary 2 and Lemma 4.    $\square$

The bound of Corollary 4 may become tighter if we actually know $\mathrm {Rank}(G/H_i)$, for all $H_i \le G$, as in Example 2.

Fig. 1.

Hasse diagram of subgroup lattice of $G = \mathbb {Z}_2 \times \mathbb {Z}_2$.

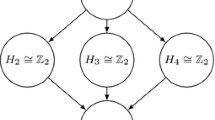
Example 3

Let $G=\mathbb {Z}_2 \times \mathbb {Z}_2$ be the Klein-four group and $A = \{ 0,1 \}$. With the notation of Example 1, Fig. 1 illustrates the Hasse diagram of the subgroup lattice of G (i.e. the actual lattice of subgroups is the transitive and reflexive closure of this graph). Hence, by Theorem 4 and Example 2,

$$\begin{aligned}&\mathrm {Rank}(\mathrm {CA}(G;A):\mathrm {ICA}(G;A)) = \vert \mathcal {E}_G \vert - 3 = 12 - 3 = 9,\\&\mathrm {Rank}(\mathrm {CA}(G;A)) \le 9 + 9 = 18, \text { as } \mathrm {Rank}(\mathrm {ICA}(G;A)) \le 9. \end{aligned}$$

Because of Theorem 4, it is particularly relevant to determine in which situations $\alpha _{[H]}(G;A)=1$. We finish this paper with some partial results in this direction that hold for arbitrary finite groups.

Denote by [G : H] the index of $H \le G$ (i.e. the number of cosets of H in G).

Lemma 7

Let G be a finite group and A a finite set of size $q\ge 2$. Assume there is $H \le G$ with $[G:H] = 2$. Then, $\alpha _{[H]} (G;A) = 1$ if and only if $q = 2$.

Proof

As $H \le G$ has index 2, it is normal. Fix $s \in G \setminus H$. Define $x \in A^G$ by

$$ (g)x = {\left\{ \begin{array}{ll} 0 &{} \text {if } g \in H \\ 1 &{} \text {if } g \in sH = Hs. \end{array}\right. } $$

Clearly $G_x = H$ and $x \in B_{[H]}$.

Suppose first that $A = \{0,1 \}$. Let $y \in B_{[H]}$. As H is normal, $[H] = \{ H\}$, so $G_y = H$. For any $h \in H$,

$$\begin{aligned} (h)y = (e)y \cdot h^{-1} = (e)y \text { and } (sh) y = (s) y \cdot h^{-1} = (s)y, \end{aligned}$$

so y is constant on the cosets H and $sH = Hs$. Therefore, either $y = x$, or

$$ (g)y = {\left\{ \begin{array}{ll} 1 &{} \text {if } g \in H \\ 0 &{} \text {if } g \in sH = Hs. \end{array}\right. } $$

In the latter case, $y \cdot s = x$ and $y \in xG$. This shows that there is a unique G-orbit contained in $B_{[H]}$, so $\alpha _{[H]}(G;A) = 1$.

If $\vert A \vert \ge 3$, we may use a similar argument as above, except that now $y \in B_{[H]}$ may satisfy $(g)y \in A \setminus \{ 0,1\}$ for all $g \in H$, so $y \not \in xG$ and $\alpha _{[H]}(G;A) \ge 2$.   $\square$

Lemma 8

Let G be a finite group and A a finite set of size $q\ge 2$. Suppose there is $H \le G$ such that $\alpha _{[H]}(G;A) = 1$. Then, $q \mid [G:H] = \frac{\vert G \vert }{\vert H \vert }$.

Proof

Let $x \in B_{[H]}$ be such that $G_x = H$. As $\alpha _{[H]}(G;A) = 1$, $B_{[H]}= xG$. First we show that $x : G \rightarrow A$ is surjective. If $(G)x \subset A$, let $a \in (G)x$ and $b \in A \setminus (G)x$. Define $y \in A^G$ by

$$ (g)y := {\left\{ \begin{array}{ll} b &{} \text { if } (g)x = a \\ (g)x &{} \text { otherwise.} \end{array}\right. }$$

Then $y \in B_{[H]}$, as $G_y = G_x$, but $y \not \in xG$, which is a contradiction. For $a \in A$, let $(a) x^{-1} := \{ g \in G : (g)x = a \}$. Now we show that, for any $a, b \in A$,

$$\begin{aligned} \vert (a)x^{-1} \vert = \vert (b)x^{-1} \vert . \end{aligned}$$

Suppose that $\vert (a)x^{-1} \vert < \vert (b)x^{-1} \vert$. Define $z \in A^G$ by

$$ (g)z := {\left\{ \begin{array}{ll} b &{} \text { if } (g)x = a \\ a &{} \text { if } (g)x = b \\ (g)x &{} \text { otherwise.} \end{array}\right. }$$

Again, $z \in B_{[H]}$, as $G_z = G_x$, but $z \not \in xG$, which is a contradiction. As x is constant on the left cosets of H in G, for each $a \in A$, $(a)x^{-1}$ is a union of left cosets. All cosets have the same size, so $(a)x^{-1}$ and $(b)x^{-1}$ contain the same number of them, for any $a,b \in A$. Therefore, $q \mid [G:H ]$.    $\square$

Corollary 5

Let G be a finite abelian group and A a finite set of size $q\ge 2$ such that $q \not \mid \vert G \vert$. With the notation of Theorem 4,

$$\begin{aligned} \mathrm {Rank}(\mathrm {CA}(G;A):\mathrm {ICA}(G;A)) = \vert \mathcal {E}_G \vert . \end{aligned}$$