An “almost dual” to Gottschalk’s Conjecture

Abstract

We discuss cellular automata over arbitrary finitely generated groups. We call a cellular automaton post-surjective if for any pair of asymptotic configurations, every pre-image of one is asymptotic to a pre-image of the other. The well known dual concept is pre-injectivity: a cellular automaton is pre-injective if distinct asymptotic configurations have distinct images. We prove that pre-injective, post-surjective cellular automata are reversible. We then show that on sofic groups, where it is known that injective cellular automata are surjective, post-surjectivity implies pre-injectivity. As no non-sofic groups are currently known, we conjecture that this implication always holds. This mirrors Gottschalk’s conjecture that every injective cellular automaton is surjective.

S. Capobianco—This research was supported by the ERDF funded project Coinduction, the Estonian Ministry of Education and Research institutional research grant IUT33-13, and the Estonian Science Foundation grant no. 9398.

S. Taati—The work of ST is supported by ERC Advanced Grant 267356-VARIS of Frank den Hollander.

1 Introduction

Cellular automata (briefly, ca) are parallel synchronous systems on regular grids where the next state of a point depends on the current state of a finite neighborhood. The grid is determined by a finitely generated group and can be visualized as the Cayley graph of the group. In addition to being a useful tool for simulations, ca are studied as models of massively parallel computers, and as dynamical systems on symbolic spaces. From a combinatorial point of view, interesting questions arise as to how the properties of the global transition function (obtained by synchronous application of the local update rule at each point) are related to one another.

One such relation is provided by Bartholdi’s theorem [1], stating that amenable groups (i.e., those which have a finitely additive probability measure, defined on every subset, and invariant by multiplication on the left) are precisely those where the Garden of Eden theorem holds. The latter states that surjective ca are pre-injective, that is, two configurations differing only in finitely many points have equal image only if they are equal. By [7, Theorem 4.7], the Garden of Eden theorem still holds for ca on subshifts that are of finite type and are strongly irreducible. Counterexamples with generic subshifts are known already in dimension 1. Furthermore, bijectivity is always equivalent to reversibility, that is, the existence of an inverse that is itself a ca.

A very remarkable consequence of the Garden of Eden theorem is that amenable groups are surjunctive: that is, every ca on an amenable group, which is injective on the full shift of all the possible configurations, is surjective. On the other hand, it is easy to prove that the free group on two generators, which is the main example of non-amenable group, is also surjunctive. Indeed, at the present time, not a single example of injective, non-surjective ca is known! This led Gottschalk to conjecture, in his 1973 paper [8], that all groups are actually surjunctive. The conjecture is known to hold for the class of sofic groups, originally defined by Gromov in the context of geometric group theory. Remarkably, no examples of non-sofic groups are known at the present time.

In this paper, which expands our previous work from Automata 2015 [4], we discuss post-surjectivity, a parallel property to pre-injectivity, which we define as follows: however given a configuration c and a preimage e, every configuration $c'$ asymptotic to c has a pre-image $e'$ asymptotic to e. While pre-injectivity is weaker than injectivity, post-surjectivity turns out to be stronger than surjectivity. It is natural to ask whether such trade-off between injectivity and surjectivity preserves bijectivity.

First, we prove that post-surjectivity and pre-injectivity together imply reversibility: that is, the trade-off above actually holds over all groups. Next, we show that, in the context of sofic groups, post-surjectivity actually implies pre-injectivity. From all this we formulate an “almost dual” to Gottschalk’s conjecture, that every post-surjective ca is pre-injective—or, equivalently, reversible.

2 Background

Let X be a set. We indicate by $\mathcal {PF}(X)$ the collection of all finite subsets of X. If X is finite, we indicate by |X| the number of its elements.

Let $\mathbb {G}$ be a group and let $U, V \subseteq \mathbb {G}$. We put $UV = \{ x \cdot y \mid x \in U, y \in V \},$ and $U^{-1} = \{ x^{-1} \mid x \in U \}.$ If $U = \{ g \}$ we write gV for $\{g\} V$.

A labeled graph is a triple $(V, L, E)$ where V is a set of vertices, L is a set of labels, and $E \subseteq V \times L \times V$ is a set of labeled edges. A labeled graph isomorphism from $(V_1, L, E_1)$ to $(V_2, L, E_2)$ is a bijection $\phi : V_1 \rightarrow V_2$ such that, for every $x, y \in V_1$ and $\ell \in L$, $(x, \ell , y) \in E_1$ if and only if $(\phi (x), \ell , \phi (y)) \in E_2.$ We will sometimes say that (V, E) is an L-labeled graph to mean that (V, L, E) is a labeled graph.

A subset $B$ of $\mathbb {G}$ is a set of generators for $\mathbb {G}$ if every $g \in \mathbb {G}$ can be written as $g = x_0 \cdots x_{n-1}$ for suitable $n \ge 0$ and $x_0, \ldots , x_{n-1} \in B\cup B^{-1}.$ The group $\mathbb {G}$ is finitely generated (briefly, f.g.) if $B$ can be chosen finite.

Let $B$ be a finite set of generators for the group $\mathbb {G}$. The Cayley graph of $\mathbb {G}$ w.r.t. $B$ is the $(B\cup B^{-1})$-labeled graph $(\mathbb {G},E)$ where $E = \{ (g, x, h) \mid gx = h \}.$ The length of $g \in \mathbb {G}$ with respect to $B$ is the minimum length $n = \Vert g\Vert _B$ of a representation $g = x_0 \cdots x_{n-1}$. The distance between g and h with respect to $B$ is $d_B(g, h) = \Vert g^{-1} \cdot h\Vert _B,$ i.e., the length of the shortest path from g to h in the Cayley graph of $\mathbb {G}$ with respect to $B$. The disk of center g and radius r with respect to $B$ is the set $D_{B,r}(g)$ of those $h \in \mathbb {G}$ such that $d_B(g, h) \le r$. We omit g if it is the identity element $1_\mathbb {G}$ of $\mathbb {G}$ and write $D_{B, r}$ for $D_{B,r}(1_\mathbb {G})$. The distance between two subsets $U, V \subseteq \mathbb {G}$ is $d_B(U, V) = \inf \{ d_B(u, v) \mid u \in U, v \in V \}.$ We omit $B$ if irrelevant or clear from the context.

A group $\mathbb {G}$ is amenable if for every $K \in \mathcal {PF}(\mathbb {G})$ and every $\varepsilon >0$ there exists a nonempty $F \in \mathcal {PF}(\mathbb {G})$ such that $|F \cap kF| > (1 - \varepsilon ) |F|$ for every $k \in K$. The groups $\mathbb {Z}^d$ are amenable, whereas the free groups on two or more generators are not. For an introduction to amenability see, e.g., [5, Chapter 4].

Let S be a finite set and let $\mathbb {G}$ be a group. The elements of the set $S^\mathbb {G}$ are called configurations. The space $S^\mathbb {G}$ is given the product topology by considering S as a discrete set. This makes $S^\mathbb {G}$ a compact space by Tychonoff’s theorem. In the prodiscrete topology, two configurations are “near” if they coincide on a “large” finite subset of $\mathbb {G}$. Indeed, if $B$ is a finite set of generators for $\mathbb {G}$, then setting $d_B(c, e) = 2^{-n},$ where n is the smallest $r \ge 0$ such that c and e differ on $D_{B,r}$, defines a distance that induces the prodiscrete topology. Given $c, c' \in S^\mathbb {G},$ we call $\varDelta (c, c') = \{ g \in \mathbb {G}\mid c(g) \ne c'(g) \}$ the difference set of c and $c'$. Two configurations are asymptotic if they differ at most on finitely many points of $\mathbb {G}$. A pattern is a function $p : E \rightarrow S$ where E is a finite subset of $\mathbb {G}$.

For $g \in \mathbb {G}$, the translation by g is the function $\sigma _g : S^\mathbb {G}\rightarrow S^\mathbb {G}$ that sends an arbitrary configuration c into the configuration $\sigma _g(c)$ defined by

$$\begin{aligned} \sigma _g(c)(x) = c(g \cdot x) \;\; \forall x \in \mathbb {G}\,. \end{aligned}$$

(1)

A shift subspace (briefly, subshift) is a subset X of $S^\mathbb {G}$ which is closed (equivalently, compact) and invariant by translation. The set $S^\mathbb {G}$ itself is referred to as the full shift. It is well known (cf. [12]) that every subshift is determined by a set of forbidden patterns, in the sense that the elements of the subshift are precisely those configurations in which the translations of the forbidden patterns do not occur. If such set can be chosen finite, X is called a shift of finite type (briefly, sft). A pattern that appears on some configuration in X is said to be admissible for X. The set of patterns that are admissible for X is called the language of X, indicated as $\mathcal {L}_X$.

A cellular automaton (briefly, ca) on a group $\mathbb {G}$ is a triple $\mathcal {A}= \langle S, \mathcal {N}, f \rangle$ where the set of states S is finite and has at least two elements, the neighborhood $\mathcal {N}$ is a finite subset of $\mathbb {G}$, and the local update rule is a function that associates to every pattern $p : \mathcal {N}\rightarrow S$ a state $f(p) \in S$. The global transition function of $\mathcal {A}$ is the function $F_\mathcal {A}: S^\mathbb {G}\rightarrow S^\mathbb {G}$ defined by

$$\begin{aligned} F_\mathcal {A}(c) (g) = f \left( \left. {(\sigma _g(c))}\right| _{{\mathcal {N}}} \right) \;\; \forall g \in \mathbb {G}\,, \end{aligned}$$

(2)

that is, if $\mathcal {N}= \{ n_1, \ldots , n_m \},$ then $F_\mathcal {A}(c)(g) = f \left( c(g \cdot n_1), \ldots , c(g \cdot n_m) \right) .$ Observe that (2) is continuous in the prodiscrete topology and commutes with the translations, i.e., $F_\mathcal {A}\circ \sigma _g = \sigma _g \circ F_\mathcal {A}$ for every $g \in \mathbb {G}$. The Curtis-Hedlund-Lyndon theorem states that the continuous and translation-commuting functions from $S^\mathbb {G}$ to itself are precisely the ca global transition functions.

We shall use the following notation to represent the application of the local rule on patterns. If $p : E \rightarrow S$ and $q : C \rightarrow S$ are two patterns, we write $p \xrightarrow {f} q$ to indicate that $C\mathcal {N}\subseteq E$ and $q(g) = f \left( \left. {(\sigma _g(p))}\right| _{{\mathcal {N}}} \right)$ for each $g\in C$.

If X is a subshift and $F_\mathcal {A}$ is a cellular automaton, it is easy to see that $F_\mathcal {A}(X)$ is also a subshift. If, in addition, $F_\mathcal {A}(X) \subseteq X,$ we say that $\mathcal {A}$ is a ca on the subshift X. From now on, when we speak of cellular automata on $\mathbb {G}$ without specifying any subshift, we will imply that such subshift is the full shift.

We may refer to injectivity, surjectivity, etc. of the cellular automaton $\mathcal {A}$ on the subshift X meaning the corresponding properties of $F_\mathcal {A}$ when restricted to X. From basic facts about compact spaces, it follows that the inverse of the global transition function of a bijective cellular automaton $\mathcal {A}$ is itself the global transition function of some cellular automaton. In this case, we say that $\mathcal {A}$ is reversible. A group $\mathbb {G}$ is surjunctive if for every finite set S, every injective cellular automaton on the full shift $S^\mathbb {G}$ is surjective. Currently, there are no known examples of non-surjunctive groups.

Conjecture 1

(Gottschalk  [8]). Every group is surjunctive.

If $\mathbb {G}$ is a subgroup of $\varGamma$ and $\mathcal {A}= \langle S, \mathcal {N}, f \rangle$ is a cellular automaton on $\mathbb {G}$, the cellular automaton $\mathcal {A}^\varGamma$ induced by $\mathcal {A}$ on $\varGamma$ has the same set of states, neighborhood, and local update rule as $\mathcal {A}$, and maps $S^\varGamma$ (instead of $S^\mathbb {G}$) into itself via $F_{\mathcal {A}^\varGamma }(c)(\gamma ) = f \left( c(\gamma \cdot n_1), \ldots , c(\gamma \cdot n_m) \right)$ for every $\gamma \in \varGamma$. We also say that $\mathcal {A}$ is the restriction of $\mathcal {A}^\varGamma$ to $\mathbb {G}$. In addition, if $X \subseteq S^\mathbb {G}$ is a subshift defined by a set F of forbidden patterns on $\mathbb {G}$, then the subshift $X^\varGamma \subseteq S^\varGamma$ obtained from the same set F of forbidden patterns satisfies the following property: if $\mathcal {A}$ is a ca on X, then $\mathcal {A}^\varGamma$ is a ca on $X^\varGamma$, and vice versa. (Here, it is fundamental that all the forbidden patterns have their supports in $\mathbb {G}$.) It turns out (cf. [5, Section 1.7] or [2, Theorem 5.3]) that injectivity and surjectivity are preserved by both induction and restriction.

Let $\mathcal {A}= \langle S, \mathcal {N}, f \rangle$ be a ca on a subshift X, let $p : E \rightarrow S$ be an admissible pattern for X, and let $E \mathcal {N}\subseteq M \in \mathcal {PF}(\mathbb {G}).$ A pre-image of p on M under $\mathcal {A}$ is a pattern $q : M \rightarrow S$ that is admissible for X such that $q \xrightarrow {f} p$. An orphan is an admissible pattern that has no admissible pre-image, or equivalently, a pattern that is admissible for X but not admissible for $F_\mathcal {A}(X)$. Similarly, a configuration which is not in the image of X by $F_\mathcal {A}$ is a Garden of Eden for $\mathcal {A}$. By a compactness argument, every Garden of Eden contains an orphan. We call this the orphan pattern principle. A cellular automaton $\mathcal {A}$ is pre-injective if every two asymptotic configurations c, e satisfying $F_\mathcal {A}(c) = F_\mathcal {A}(e)$ are equal. The Garden of Eden theorem (cf. [6]) states that, for ca on amenable groups, pre-injectivity is equivalent to surjectivity; on non-amenable groups, the two properties appear to be independent of each other.

Definition 1

Let $\mathbb {G}$ be a finitely generated group, let $B$ be a finite set of generators for $\mathbb {G}$, and let S be a finite set. A subshift $X \subseteq S^\mathbb {G}$ is strongly irreducible if there exists $r \ge 0$ such that, for every two admissible patterns $p_1 : E_1 \rightarrow S, p_2 : E_2 \rightarrow S$ such that $d_B(E_1, E_2) \ge r,$ there exists $c \in X$ such that $\left. {c}\right| _{{E_1}} = p_1$ and $\left. {c}\right| _{{E_2}} = p_2.$ We then say that r is a constant of strong irreducibility for X with respect to $B$.

The notion of strong irreducibility does not depend on the choice of the finite set of generators, albeit the associated constant of strong irreducibility usually does. If no ambiguity is possible, we will suppose $B$ fixed once and for all, and always speak of r relative to $B$. For $\mathbb {G}=\mathbb {Z}$, strong irreducibility is equivalent to existence of $r \ge 0$ such that, for every two $u, v \in \mathcal {L}_X,$ there exists $w \in S^r$ satisfying $u w v \in \mathcal {L}_X.$

As a consequence of the definition, strongly irreducible subshifts are mixing: given two open sets $U,V\subseteq X$, the set of those $g\in \mathbb {G}$ such that $U \cap \sigma _g(V) = \emptyset$ is, at most, finite. In addition to this, as by [12, Theorem 8.1.16], the Garden of Eden theorem is still valid on strongly irreducible subshifts. We remark that for one-dimensional subshifts of finite type, strong irreducibility is equivalent to the mixing property.

Another property of strongly irreducible subshifts, which will have a crucial role in the next section, is that they allow a “cut and paste” technique which is very common in proofs involving the full shift, but may be inapplicable for more general shifts.

Proposition 1

Let $X \subseteq S^\mathbb {G}$ be a strongly irreducible subshift, let $c \in X$, and let $p : E \rightarrow S$ be an admissible pattern for X. There exists $c' \in X$ asymptotic to c such that $\left. {c'}\right| _{{E}} = p.$

Proof

It is not restrictive to suppose $E = D_n$ for suitable $n \ge 0$. Let $r \ge 0$ be a constant of strong irreducibility for X. Writing $E_k = D_{n+r+k} \setminus D_{n+r}$ for $k \ge 1$, we have of course $d(E, E_k) = r.$ Set $p_k = \left. {c}\right| _{{E_k}}.$ By strong irreducibility, there exists $c_k \in X$ such that $\left. {c_k}\right| _{{E}} = p$ and $\left. {c_k}\right| _{{E_k}} = p_k.$ Then every limit point $c'$ of $\{c_k\}_{k \ge 1},$ which exists and belongs to X because of compactness, satisfies the thesis.    $\square$

3 Post-surjectivity

The notion of post-surjectivity is a sort of “dual” to pre-injectivity: it is a strengthening of surjectivity, in a similar way that pre-injectivity is a weakening of injectivity. The maps that are both pre-injective and post-surjective were studied in [11] under the name of complete pre-injective maps.

Definition 2

Let $\mathbb {G}$ be a group, S a finite set, and $X \subseteq S^\mathbb {G}$ a strongly irreducible shift of finite type. A cellular automaton $\mathcal {A}= \langle S, \mathcal {N}, f \rangle$ on X is post-surjective if, however given $c \in X$ and a predecessor $e \in X$ of c, every configuration $c' \in X$ asymptotic to c has a predecessor $e' \in X$ asymptotic to e.

When $X = S^\mathbb {G}$ is the full shift, if no ambiguity is present, we will simply say that the ca is post-surjective.

Example 1

Every reversible cellular automaton is post-surjective. If $R \ge 0$ is a neighborhood radius for the inverse ca, and c and $c'$ coincide outside $D_N$, then their unique pre-images e and $e'$ must coincide outside $D_{N+R}$.

Example 2

The $\mathrm {xor}$ ca with the right-hand neighbor (the one-dimensional elementary ca with rule 102) is surjective, but not post-surjective. As the $\mathrm {xor}$ function is a permutation of each of its arguments given the other, every $c \in \{0,1\}^\mathbb {Z}$ has two pre-images, uniquely determined by their value in a single point. However (actually, because of this!) $\ldots 000 \ldots$ is a fixed point, but $\ldots 010 \ldots$ only has pre-images that take value 1 infinitely often.

The qualification “post-surjective” is well earned:

Proposition 2

Let $X \subseteq S^\mathbb {G}$ be a strongly irreducible sft. Every post-surjective ca on X is surjective.

Proof

Let $r \ge 0$ be the constant of strong irreducibility of X, i.e., let every two admissible patterns whose supports have distance at least r be jointly subpatterns of some configuration. Take an arbitrary $e \in X$ and set $c = F(e)$. Let $p : E \rightarrow S$ be an admissible pattern for X. By Proposition 1, there exists $c' \in X$ asymptotic to c such that $\left. {c'}\right| _{{E}} = p.$ By post-surjectivity, such $c'$ has a pre-image in X, which means p has a pre-image admissible for X. The thesis follows from the orphan pattern principle.    $\square$

From Proposition 2 together with [7, Theorem 4.7] follows:

Proposition 3

Let $\mathbb {G}$ be an amenable group and let $X \subseteq S^\mathbb {G}$ be a strongly irreducible sft. Every post-surjective ca on X is pre-injective.

In addition, via a reasoning similar to the one employed in [5, Sect. 1.7] and [3, Remark 18], we can prove:

Proposition 4

Let $\mathcal {A}= \langle S, \mathcal {N}, f \rangle$ be a cellular automaton on the group $\mathbb {G}$, let $\varGamma$ be a group that contains $\mathbb {G}$, and let $\mathcal {A}^\varGamma$ be the ca induced by $\mathcal {A}$ on $\varGamma$. Then $\mathcal {A}$ is post-surjective on $S^\mathbb {G}$ if and only if $\mathcal {A}^\varGamma$ is post-surjective on $S^\varGamma$.

In particular, post-surjectivity of arbitrary ca is equivalent to post-surjectivity on the subgroup generated by the neighborhood.

Proof

Suppose that $\mathcal {A}$ is post-surjective. Let J be a set of representatives of the left cosets of $\mathbb {G}$ in $\varGamma$, i.e., let $\varGamma = \bigsqcup _{j \in J} j\mathbb {G}.$ Let $c, c' \in S^\varGamma$ two asymptotic configurations and let e be a pre-image of c. For every $j \in J$ and $g \in \mathbb {G}$ set

$$\begin{aligned} c_j(g)= & {} c(j \cdot g) \,; \\ c'_j(g)= & {} c'(j \cdot g) \,; \\ e_j(g)= & {} e(j \cdot g) \,. \end{aligned}$$

By construction, $c_j$ is asymptotic to $c'_j$ and has $e_j$ as a pre-image according to $\mathcal {A}$. Moreover, as c and $c'$ are asymptotic in the first place, $c'_j \ne c_j$ only for finitely many $j \in J$. For every $j \in J$ let $e'_j \in S^\mathbb {G}$ be a pre-image of $c_j'$ according to $\mathcal {A}$ asymptotic to $e_j$, if $c'_j \ne c_j$, and $e_j$ itself if $c'_j = c_j$. Then,

$$\begin{aligned} e'(\gamma ) = e_j(g) \;\; \iff \;\; \gamma = j \cdot g \end{aligned}$$

defines a pre-image of $c'$ asymptotic to e according to $\mathcal {A}^\varGamma$.

The converse implication is immediate.    $\square$

Example 3

Let $X \subseteq S^\mathbb {Z}$ be a one-dimensional strongly irreducible sft and let $\mathcal {A}= \langle S, \mathcal {N}, f \rangle$ be a post-surjective ca on X. Then $\mathcal {A}$ is reversible.

Suppose it is not so. For ca on one-dimensional strongly irreducible sft, reversibility is equivalent to injectivity on periodic configurations. Namely, if two distinct configurations with the same image exist, then one can construct two distinct periodic configurations with the same image. Let then $u, v, w \in S^*$ be such that $e_u = \ldots u u u \ldots ,$ the configuration obtained by extending u periodically in both directions, and $e_v = \ldots v v v \ldots$ are different and have the same image $c = \ldots w w w \ldots .$ It is not restrictive to suppose $|u| = |v| = |w|$. Without loss of generality, we also assume that X is defined by a set of forbidden words of length at most |u|.

Let $r \ge 0$ be a strong irreducibility constant for X and let $p, q \in S^r$ be such that $u p v, v q u \in \mathcal {L}_X.$ The two configurations $c_{u,v} = F( \ldots u u p v v \ldots )$ and $c_{v,u} = F( \ldots v v q u u \ldots )$ are both asymptotic to c. By post-surjectivity, there exist $x,y\in \mathcal {L}_X$ such that $e_{u,v} = \ldots u u x v v \ldots$ and $e_{v,u} = \ldots v v y u u \ldots$ satisfy $F( e_{u,v} ) = F( e_{v,u} ) = c.$ Again, it is not restrictive to suppose that $|x| = |y| = m \cdot |u|$ for some $m \ge 1$, and that x and y start in $e_{u,v}$ and $e_{v,u}$ at the same point $i \in \mathbb {Z}$.

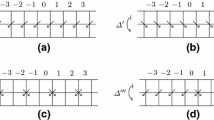
Let us now consider the configuration $e' = \ldots u u x v^N y u u \ldots .$ By our previous discussion, for N large enough (e.g., so that x and y do not have overlapping neighborhoods) $F_\mathcal {A}(e')$ cannot help but be c. Now, recall that $e_u$ is also a pre-image of c and note that $e_u$ and $e'$ are asymptotic but distinct. Then $\mathcal {A}$ is surjective, but not pre-injective, contradicting the Garden of Eden theorem [12, Theorem 8.1.16] (Fig. 1).

Fig. 1.

A graphical description of the argument in Example 3 for the full shift. (a) Let a 1D periodic configuration w have two different (periodic) preimages u and v. (b) By swapping the right-hand halves of the preimages, the new images only differ from the initial one in finitely many points. (c) By post-surjectivity, we can change them in finitely many points, and get two preimages of the initial configuration. (d) Then a violation of the Garden of Eden theorem occurs.

Example 3 depends critically on dimension 1, where ca that are injective on periodic configurations are reversible. Moreover, in our final step, we invoke the Garden of Eden theorem, which we know from [1, 6] not to hold for ca on generic groups. Not all is lost, however: maybe, by explicitly adding the pre-injectivity requirement, we can recover Example 3 on more general groups?

It turns out that it is so, at least for ca on full shifts. To see this, we need a preliminary lemma.

Lemma 1

Let $\mathcal {A}$ be a post-surjective ca on a finitely generated group $\mathbb {G}$ and let F be its global transition function. There exists $N \ge 0$ such that, given any three configurations $c, c', e$ with $c = F(e)$ and $\varDelta (c, c') = \{1_\mathbb {G}\}$, there exists a pre-image $e'$ of $c'$ which coincides with e outside $D_N$.

Proof

By contradiction, assume that for every $n \ge 0$ there exist $c_n \in S^\mathbb {G}, e_n \in F^{-1}(c_n),$ and $c'_n \ne c_n$ such that $\varDelta (c_n, c'_n) = \{ 1_\mathbb {G}\},$ but every $e'_n \in F^{-1}(c'_n)$ differs from $e_n$ on some point outside $D_n$. By compactness, there exits a sequence $n_i$ such that the limits $c = \lim _{i \rightarrow \infty } c_{n_i}, c' = \lim _{i \rightarrow \infty } c'_{n_i},$ and $e = \lim _{i \rightarrow \infty } e_{n_i},$ all exist. Then $F(e) =c$ by continuity. By construction, c differs from $c'$ only at $1_\mathbb {G}$. By post-surjectivity, there exists a pre-image $e'$ of $c'$ such that $\varDelta (e, e') \subseteq D_m$ for some $m \ge 0$. Take $\ell \gg m$ and choose k large enough such that $\left. {c'_{n_k}}\right| _{{D_{\ell }}} = \left. {c'}\right| _{{D_{\ell }}}$ and $\left. {e_{n_k}}\right| _{{D_{\ell }}} = \left. {e}\right| _{{D_{\ell }}}.$ Define $\tilde{e}$ so that it agrees with $e'$ on $D_{\ell }$ and with $e_{n_k}$ outside $D_m$. Such $\tilde{e}$ does exist, because $e'$, e, and $e_{n_k}$ agree on $D_{\ell } \setminus D_m$. Then $\tilde{e}$ is a pre-image of $c'_{n_k}$ which is asymptotic to $e_{n_k}$ and agrees with $e_{n_k}$ outside $D_{n_k}$, thus contradicting our assumption.    $\square$

By repeatedly applying Lemma 1 we get:

Corollary 1

Let $\mathcal {A}$ be a post-surjective ca on a finitely generated group $\mathbb {G}$ and let F be its global transition function. There exists $N\ge 0$ such that, for every $r \ge 0$, however given three configurations $c,c',e$ with $c=F(e)$ and $\varDelta (c,c')\subseteq D_r,$ there exists a pre-image $e'$ of $c'$ such that $\varDelta (e, e') \subseteq D_{N+r}.$

Assuming also pre-injectivity, we get the following stronger property:

Corollary 2

Let $\mathcal {A}$ be a pre-injective, post-surjective ca on a finitely generated group $\mathbb {G}$ and let F be its global transition function. There exists $M \in \mathcal {PF}(\mathbb {G})$ with the following property: For every pair $(e, e')$ of asymptotic configurations, if $c = F(e)$ and $c' = F(e')$ disagree at most on K, then e and $e'$ disagree at most on KM.

We are now ready to prove:

Theorem 1

Every pre-injective, post-surjective cellular automaton on the full shift is reversible.

Proof

By Proposition 4, it is sufficient to consider the case where $\mathbb {G}$ is finitely generated.

Let $\mathcal {A}$ be a pre-injective and post-surjective ca on the group $\mathbb {G}$, let S be its set of states, and let F be its global transition function. Let M be as in Corollary 2. We construct a new ca with neighborhood $\mathcal {N}= M^{-1}$. Calling H the global transition function of the new ca, we first prove that H is a right inverse of F. We then show that H is also a left inverse for F, thus completing the proof.

To construct the local update rule $h : S^\mathcal {N}\rightarrow S$, we proceed as follows. Fix a uniform configuration u and let $v=F(u)$. Given $g\in \mathbb {G}$ and $p : \mathcal {N}\rightarrow S$, for every $i\in \mathbb {G}$, put

$$\begin{aligned} y_{g,p}(i) = \left\{ \begin{array}{ll} p(g^{-1} i) &{} \mathrm {if} \; i \in g \mathcal {N}\\ {v(i)} &{} \mathrm {otherwise} \end{array} \right. \end{aligned}$$

(3)

that is, let $y_{g,p}$ be obtained from v by cutting away the piece with support $g \mathcal {N}$ and pasting p as a “patch” for the “hole”. By post-surjectivity and pre-injectivity combined, there exists a unique $x_{g,p} \in S^\mathbb {G}$ asymptotic to u such that $F(x_{g,p}) = y_{g,p}$. Let then

$$\begin{aligned} h(p) = x_{g,p}(g) \,. \end{aligned}$$

(4)

Observe that (4) does not depend on g: if $g' = i \cdot g$, then $y_{g',p} = \sigma _i ( F(x_{g,p}) ) = F( \sigma _i(x_{g,p}) ),$ so that $x_{g', p} = \sigma _i ( x_{g, p} )$ by pre-injectivity, and $x_{g', p} (g') = x_{g, p} (g).$

Let now y be any configuration asymptotic to v such that $\left. {y}\right| _{{g\mathcal {N}}} = p$, and let x be the unique pre-image of y asymptotic to u. We claim that $x(g) = h(p)$. To prove this, we observe that, as y and $y_{g, p}$ are both asymptotic to v and they agree on $g \mathcal {N}= g M^{-1},$ the set K where they disagree is finite and is contained in $\mathbb {G}\setminus g M^{-1}.$ By Corollary 2, their pre-images x and $x_{g,p}$ can disagree only on $K M \subseteq \left( \mathbb {G}\setminus gM^{-1} \right) M.$ The set KM does not contain g, because if $g \in \left( \mathbb {G}\setminus gM^{-1} \right) M,$ then for some $m \in M$, $g m^{-1} \in \left( \mathbb {G}\setminus gM^{-1} \right) ,$ which is not the case! Therefore, $x(g) = x_{g,p}(g) = h(p),$ as we claimed.

The argument above holds whatever the pattern $p:\mathcal {N}\rightarrow S$ is. By applying it finitely many times to arbitrary finitely many points, we find the following fact: if y is any configuration which is asymptotic to v, then $F(H(y)) = y$. But the set of configurations asymptotic to v is dense in $S^\mathbb {G}$, so it follows from continuity of F and H that $F(H(y))=y$ for every $y\in S^\mathbb {G}$.

We have thus shown that H is a right inverse of F. We next verify that H is also a left inverse of F.

Let x be a configuration asymptotic to u, and set $y=F(x)$. Note that y is asymptotic to v. The two configurations x and H(y) are both asymptotic to u, and furthermore, $F(x)=y=F(H(y))$. Therefore, by the pre-injectivity of F, x and H(y) must coincide, that is, $H(F(x))=x$. The continuity of F and H now implies that the equality $H(F(x))=x$ holds even if x is not asymptotic to u. Hence, H is a left inverse for F.    $\square$

Corollary 3

A cellular automaton on an amenable group (in particular, a d-dimensional ca) is post-surjective if and only if it is reversible.

4 Post-surjectivity on Sofic Groups

After proving Theorem 1, we might want to show examples of post-surjective cellular automata which are not pre-injective. However, the standard examples of surjective ca which are not pre-injective, such as the majority rule on the free group on two generators, fail to work. The reason is that, as we shall see below, finding such a counterexample amounts to finding a group which is not sofic, and that appears to be a difficult open problem.

The notion of sofic group was originally introduced by Gromov [9], but was later reformulated by Weiss [13] in combinatorial, rather than geometric, terms.

Definition 3

Let $\mathbb {G}$ be a finitely generated group and let $B$ be a finite symmetric set of generators for $\mathbb {G}$. Let $r \ge 0$ be an integer and $\varepsilon > 0$ a real. An $(r,\varepsilon )$ -approximation of $\mathbb {G}$ (relative to $B$) is a $B$-labeled graph (V, E) along with a subset $U\subseteq V$ such that the following hold:

• 1. For every $u \in U$, the neighborhood of radius r of u in (V, E) is isomorphic to $D_{B,r}$ as a labeled graph.

• 2. $|U| > (1 - \varepsilon ) |V|.$

The group $\mathbb {G}$ is sofic (relative to $B$) if for every choice of $r\ge 0$ and $\varepsilon >0$, there is an $(r,\varepsilon )$-approximation of $\mathbb {G}$ (relative to $B$).

As explained in [13], the notion of soficness does not depend on the generating set $B$. For this reason, in the rest of this section, we will suppose $B$ given once and for all. It is easy to see that finitely generated residually finite groups and finitely generated amenable groups are all sofic.

The importance of sofic groups is manifold: firstly, as per [13, Sect. 3], sofic groups are surjunctive; secondly, no examples of non-sofic groups are currently known. We add a third reason:

Theorem 2

Let $\mathbb {G}$ be a sofic group. Every post-surjective cellular automaton on $\mathbb {G}$ is pre-injective.

As a corollary, cellular automata which are post-surjective, but not pre-injective, could only exist over non-sofic groups!

To prove Theorem 2, we need two auxiliary lemmas. Observe that if $f:S^{D_R}\rightarrow S$ is the local rule of a cellular automaton on a group $\mathbb {G}$ with a finite generating set $B$, and (V, E) is a $B$-labeled graph, then f is applicable in an obvious fashion to patterns on V at every point $v\in V$ whose R-neighborhood in (V, E) is isomorphic to the disk of radius R in the Cayley graph of $\mathbb {G}$ with generating set $B$. Therefore, we extend our notation, and for two patterns $p:E\rightarrow S$ and $q:C\rightarrow S$ with $E,C\subseteq V$, we write $p\xrightarrow {f} q$ if for every $v\in C$, the R-neighborhood $D_R(v)$ is a subset of E and is isomorphic to the disk of radius R, and furthermore $f \big ( \left. {p}\right| _{{D_R(v)}} \big ) =q(v).$

Lemma 2

Let $\mathcal {A}$ be a post-surjective ca on a sofic group $\mathbb {G}$. Let $\mathcal {A}$ have state set S, neighborhood radius R and local rule f, and let N be given by Lemma 1. Consider an $(r,\varepsilon )$-approximation given by a graph (V, E) and a set $U\subseteq V$, where $\varepsilon >0$ and $r\ge N+2R$. For every pattern $q:U\rightarrow S$, there is a pattern $p:V\rightarrow S$ such that $p\xrightarrow {f}q$.

Proof

Take arbitrary $p_0:V\rightarrow S$ and $q_0:U\rightarrow S$ such that $p_0\xrightarrow {f}q_0$. Let $q_0, q_1, \ldots , q_m = q$ be a sequence of patterns with support U such that, for every i, $q_i$ and $q_{i+1}$ only differ in a single $k_i \in U$. Since the r-neighborhood of $k_i$ is isomorphic to the disk of the same radius from the Cayley graph of $\mathbb {G}$, we can apply Lemma 1 and deduce the existence of a sequence $p_0, p_1, \ldots , p_m$ with common support V such that each $p_i$ is a pre-image of $q_i$ and, for every i, $p_i$ differs from $p_{i+1}$ at most in $D_N(k_i)$. Then $p=p_m$ satisfies the thesis.    $\square$

The next lemma is an observation made in [13].

Lemma 3

(Packing lemma). Let $\mathbb {G}$ be a group with a finite generating set $B$. Let (V, E) be a $B$-labeled graph and $U\subseteq V$ a subset with $|U| \ge \frac{1}{2} |V|$ such that, for every $u\in U$, the $2\ell$-neighborhood of u in (V, E) is isomorphic to the disk of radius $2\ell$ in the Cayley graph of $\mathbb {G}$. Then, there is a set $W \subseteq U$ of size at least $\frac{|V|}{2|D_{2\ell }|}$ such that the $\ell$-neighborhoods of the elements of W are disjoint.

Proof

Let $W\subseteq U$ be a maximal set such that the $\ell$-neighborhoods of the elements of W are disjoint. Then, for every $u\in U$, the neighborhood $D_{\ell }(u)$ must intersect the set $\bigcup _{w\in W}D_\ell (w)$. Therefore, $U \subseteq D_{2\ell }(W),$ which gives $|U| \le |D_{2\ell }| \cdot |W|.$    $\square$

Proof

(of Theorem 2 ). Let $\mathbb {G}$ be a sofic group and assume that $\mathcal {A}= \langle S, D_R, f \rangle$ is a cellular automaton on $\mathbb {G}$ that is post-surjective, but not pre-injective. For brevity, set $|S| = s \ge 2$. Let N be as in Lemma 1.

Since the ca is not pre-injective, there are two asymptotic configurations $x, x' : \mathbb {G}\rightarrow S$ such that $F_\mathcal {A}(x) = F_\mathcal {A}(x').$ Take m such that the disk $D_m$ contains $\varDelta (x,x')$. It follows that there are two mutually erasable patterns on $D_{m+2R}$, that is, two patterns $p, p' : D_{m+2R} \rightarrow S$ such that on any configuration z, replacing an occurrence of p with $p'$ or vice versa does not change the image of z under $F_\mathcal {A}$.

Take $r \ge \max \{N, m\} + 2R$ and $\varepsilon >0$ small. We shall need $\varepsilon$ small enough so that

$$\begin{aligned} s^{\varepsilon } \cdot \left( 1 - s^{-|D_r|} \right) ^{\frac{1}{2|D_{2r}|}} < 1 \,. \end{aligned}$$

Such a choice is possible, because the second factor on the left-hand side is a constant smaller than 1. Since $\mathbb {G}$ is sofic, there is a $(2r,\varepsilon )$-approximation of $\mathbb {G}$ given by a graph (V, E) and a set $U\subseteq V$. Let $\varphi : S^V \rightarrow S^U$ be the map given by $\varphi (p) = q$ if $p \xrightarrow {f} q$. Such $\varphi$ is well defined, because the R-neighborhood of each $u\in U$ is isomorphic to the disk of radius R in $\mathbb {G}$.

By Lemma 2, the map $\varphi$ is surjective, hence

$$\begin{aligned} |\varphi (S^V)| = s^{|U|} \,. \end{aligned}$$

(5)

On the other hand, by Lemma 3, there is a collection $W\subseteq U$ of $|W| \ge \frac{|V|}{2|D_{2r}|}$ points in U whose r-neighborhoods are disjoint. Each of these r-neighborhoods is isomorphic to the disk $D_r \supseteq D_{m+2R}$ in $\mathbb {G}$. The existence of the mutually erasable patterns on $D_r$ thus implies that there are at most

$$\begin{aligned} |\varphi (S^V)| \le (s^{|D_r|}-1)^{|W|} \cdot s^{|V|-|W|\cdot |D_r|} \end{aligned}$$

patterns on V with distinct images. However,

$$\begin{aligned} (s^{|D_r|}-1)^{|W|} \cdot s^{|V|-|W|\cdot |D_r|}= & {} \left( 1 - s^{-|D_r|} \right) ^{|W|} \cdot s^{|V|} \\\le & {} \left( 1 - s^{-|D_r|} \right) ^{\frac{|V|}{2|D_{2r}|}} \cdot s^{|V|} \\<&s^{-\varepsilon |V|} \cdot s^{|V|} \\= & {} s^{(1-\varepsilon )|V|} \\< & {} s^{|U|} \,: \end{aligned}$$

which contradicts (5).    $\square$

Corollary 4

Let $\mathbb {G}$ be a sofic group and $\mathcal {A}$ a cellular automaton on $\mathbb {G}$. Then, $\mathcal {A}$ is post-surjective if and only if it is reversible.

5 Conclusions

We have given a little contribution to a broad research theme by examining some links between different properties of cellular automata. In particular, we have seen how reversibility can still be obtained by weakening injectivity while strengthening surjectivity. Whether other such “transfers” are possible, is a field that we believe deserving to be explored. Another interesting issue is whether post-surjective cellular automata which are not pre-injective do or do not exist. By Theorem 2, such examples might exist only if non-sofic groups exist. We thus formulate the following “almost dual” to Gottschalk’s conjecture:

Conjecture 2

Let $\mathbb {G}$ be a group and $\mathcal {A}$ a cellular automaton on $\mathbb {G}$. If $\mathcal {A}$ is post-surjective, then it is pre-injective.