Abstract
A Software Product Line (SPL) is a set of similar programs generated from a common code base. Delta Oriented Programming (DOP) is a flexible approach to implement SPLs. Efficiently type checking an SPL (i.e., checking that all its programs are well-typed) is challenging. This paper proposes a novel type checking approach for DOP. Intrinsic complexity of SPL type checking is addressed by providing early detection of type errors and by reducing type checking to satisfiability of a propositional formula. The approach is tunable to exploit automatically checkable DOP guidelines for making an SPL more comprehensible and type checking more efficient. The approach and guidelines are formalized by means of a core calculus for DOP of product lines of Java programs.
The authors of this paper are listed in alphabetical order. This work has been partially supported by: project HyVar (www.hyvar-project.eu), which has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 644298; by ICT COST Action IC1402 ARVI (www.cost-arvi.eu); and by Ateneo/CSP D16D15000360005 project RunVar.
1 Introduction
A Software Product Line (SPL) is a set of similar programs, called variants, with a common code base and well documented variability [6]. Delta-Oriented Programming (DOP) [5, 18, 19] is a flexible transformational approach to implement SPLs. A DOP product line is described by a Feature Model (FM), a Configuration Knowledge (CK), and an Artifact Base (AB). The FM provides an abstract description of variants in terms of features: each feature represents an abstract description of functionality and each variant is identified by a set of features, called a product. The AB provides language dependent code artifacts that are used to build the variants: it consists of a base program (that might be empty or incomplete) and of a set of delta modules, which are containers of modifications to a program (e.g., for Java programs, a delta module can add, remove or modify classes and interfaces). The CK connects the code artifacts in the AB with the features in the FM (thus defining a mapping from products to variants): it associates to each delta module an activation condition over the features and specifies an application ordering between delta modules [19]. DOP supports the automatic generation of variants based on a selection of features: once a user selects a product, the corresponding variant is derived by applying the delta modules with a satisfied activation condition to the base program according to the application ordering.
DOP is a generalization of Feature-Oriented Programming (FOP) [4, 9, 22]: the artifact base of a FOP product line consists of a set of feature modules which are delta modules that correspond one-to-one to features and do not contain remove operations. Hence FOP product line development always starts from base feature modules corresponding to mandatory features. Instead, DOP allows to use arbitrary code as a base program. For example, the base program can be empty and different variants can be used as base delta modules with pairwise disjoint activation conditions [20]. Therefore, DOP supports both proactive SPL development (i.e., planning all products/variants in advance) and extractive SPL development [15] (i.e., starting from existing programs). Moreover (see, e.g., [5]), the decoupling between features and delta modules allows to counter the optional feature problem [13], where additional glue code is needed in order to make optional features to cooperate properly. Due to the additional flexibility, in DOP it is more challenging than in FOP to efficiently type check a product line [5]. Type checking approaches for DOP have already been studied [5, 8], and implemented [1] for the ABS modeling language [12]. Although these approaches do not require to generate any variant, they involve an explicit iteration over the set of products, which becomes an issue when the number of products is large (a product line with n features can have up to \(2^n\) products).
In this paper we propose a novel type checking approach for DOP by building on ideas proposed for FOP [9, 22]. Our approach represents an achievement over previous type checking approaches for DOP [5, 8] since it provides earlier detection of some type errors and does not require to iterate over the set of products. Like the techniques in [9, 22], our approach requires to check the validity of a propositional formula (which is a co-NP-complete problem) and can take advantages of the many heuristics implemented in SAT solvers (a SAT solver can be used to check whether a propositional formula is valid by checking whether its negation is unsatisfiable)—[9, 22] report that the performance of using SAT solvers to verify the propositional formulas for four non-trivial product lines was encouraging and that, for the largest product line, applying the approach was even faster than generating and compiling a single product. Moreover, our approach is designed to be tunable to take advantage of automatically checkable DOP guidelines that make a product line more comprehensible and type checking more efficient. We formalize the approach and guidelines by means of Imperative Featherweight Delta Java (IF\(\varDelta \)J) [5], a core calculus for DOP product lines where variants are written in an imperative version of Featherweight Java (FJ) [11].
Section 2 introduces an example that will be used through the paper and recalls IF\(\varDelta \)J. Section 3 introduces two DOP guidelines (no-useless-operations and type-uniformity). Section 4 gives a version of the approach tuned to exploit type-uniformity. Section 5 outlines a version that exploits no guidelines. Section 6 proposes other guidelines. Section 7 discusses related work. Section 8 concludes the paper by outlining planned future work. Proofs of the main results and a prototypical implementation are available in [2] (currently only the version of the approach in Sect. 4 is supported).
2 Model
In this section we introduce the running example of this paper and briefly recall the IF\(\varDelta \)J [5] core calculus. A product line L consist of a feature model, a configuration knowledge, and an artifact base. In IF\(\varDelta \)J there is no concrete syntax for the feature model and the configuration knowledge. We use the following notations:  is the set of features;
is the set of features;  specifies the products (i.e., a subset of the power set
specifies the products (i.e., a subset of the power set  );
);  maps each delta module name d to its activation condition; and
maps each delta module name d to its activation condition; and  (or
(or  , for short) is the application ordering between the delta modules. Both the set of valid products and the activation condition of the delta modules are expressed as propositional logic formulas \(\varPhi \) where propositional variables are feature names \(\varphi \) (see [3] for a discussion on other possible representations):
, for short) is the application ordering between the delta modules. Both the set of valid products and the activation condition of the delta modules are expressed as propositional logic formulas \(\varPhi \) where propositional variables are feature names \(\varphi \) (see [3] for a discussion on other possible representations):

As usual, we say that a propositional formula \(\varPhi \) is valid if it is true for all values of its propositional variables. To avoid over-specification, the order  can be partial. We assume unambiguity of the product line, i.e., for each product, any total ordering of the activated delta modules that respects
can be partial. We assume unambiguity of the product line, i.e., for each product, any total ordering of the activated delta modules that respects  generates the same variant. We refer to [5, 16] for a discussion on an effective means to ensure unambiguity.
generates the same variant. We refer to [5, 16] for a discussion on an effective means to ensure unambiguity.
The running example of this paper is a version of the Expression Product Line (EPL) benchmark [17] (see also [5]) defined by the following grammar which describes a language of numerical expressions:

Each variant of the EPL contains a class Exp that represents an expression equipped with a subset of the following operations: toInt, which returns the value of the expression as an integer (an object of class Int); toString, which returns the expression as a String; and eval, which in some variants returns the value of the expression as a Lit (the subclass of Exp representing literals) and in the other variants returns it as an Int. The EPL has 6 products, described by two feature sets: one concerned with data—fLit, fAdd—and one concerned with operations —fToInt, fToString, fEval1, fEval2. Features fLit and fToInt are mandatory. The other features are optional with the two following constraints: exactly one between fEval1 and fEval2 must be selected; and fEval1 requires fToString. The EPL is illustrated in Fig. 1. The partial order  is expressed as a total order on a partition of the set of delta modules. To make the example more readable, in the artifact base we use the Java syntax for operations on strings and sequential composition —encoding in IF\(\varDelta \)J syntax is straightforward (see [5] for examples). Note that, in the method Test.test (in the base program), the expression x.eval() has type Lit if feature fEval1 is selected (for this reason feature fEval1 requires feature fToString) and type Int otherwise.
is expressed as a total order on a partition of the set of delta modules. To make the example more readable, in the artifact base we use the Java syntax for operations on strings and sequential composition —encoding in IF\(\varDelta \)J syntax is straightforward (see [5] for examples). Note that, in the method Test.test (in the base program), the expression x.eval() has type Lit if feature fEval1 is selected (for this reason feature fEval1 requires feature fToString) and type Int otherwise.
In the following, we first introduce the IFJ calculus, which is an imperative version of FJ [11], and then we introduce the constructs for variability on top of it. The abstract syntax of IFJ is presented in Fig. 2 (top). Following [11], we use the overline notation for (possibly empty) sequences of elements: for instance \(\overline{e}\) stands for a sequence of expressions. Variables x include the special variable this (implicitly bound in any method declaration MD), which may not be used as the name of a method’s formal parameter. A program P is a sequence of class declarations \(\overline{CD}\). A class declaration  comprises the name C of the class, the name
comprises the name C of the class, the name  of the superclass (which must always be specified, even if it is the built-in class Object), and a list of field and method declarations \( \overline{AD}\). All fields and methods are public, there is no field shadowing, there is no method overloading, and each class is assumed to have an implicit constructor that initializes all fields to
of the superclass (which must always be specified, even if it is the built-in class Object), and a list of field and method declarations \( \overline{AD}\). All fields and methods are public, there is no field shadowing, there is no method overloading, and each class is assumed to have an implicit constructor that initializes all fields to  . The subtyping relation \(<:\) on classes, which is the reflexive and transitive closure of the immediate subclass relation (given by the
. The subtyping relation \(<:\) on classes, which is the reflexive and transitive closure of the immediate subclass relation (given by the  clauses in class declarations), is assumed to be acyclic. Type system, operational semantics, and type soundness for IFJ are given in [5].
clauses in class declarations), is assumed to be acyclic. Type system, operational semantics, and type soundness for IFJ are given in [5].
The abstract syntax of the language IF\(\varDelta \)J is given in Fig. 2 (bottom). An IF\(\varDelta \)J program L comprises: a feature model \(FM\), a configuration knowledge \(CK\), and an artifact base AB. Recall that we do not consider a concrete syntax for \(FM\) and \(CK\) and use the notations  , and
, and  (
( for short) introduced above. The artifact base comprises a possibly empty or incomplete IFJ program P, and a set of delta modules \({\overline{\varDelta }}\).
for short) introduced above. The artifact base comprises a possibly empty or incomplete IFJ program P, and a set of delta modules \({\overline{\varDelta }}\).
A delta module declaration \(\varDelta \) comprises the name d of the delta module and class operations \(\overline{CO}\) representing the transformations performed when the delta module is applied to an IFJ program. A class operation can add, remove, or modify a class. A class can be modified by (possibly) changing its super class and performing attribute operations \(\overline{AO}\) on its body. An attribute name a is either a field name \({\texttt {f}}\) or a method name m. An attribute operation can add or remove fields and methods, and modify the implementation of a method by replacing its body. The new body may call the special method \(\texttt {original}\), which is implicitly bound to the previous implementation of the method and may not be used as the name of a method. The class operations in a delta module must act on distinct classes, and the attribute operations in a class operation must act on distinct attributes. The operational semantics of IF\(\varDelta \)J variant generation is given in [5].
We conclude this section with some notations and definitions. First, in the rest of the document, we will use the term module to refer to the base program or a delta module: we denote with p the name of the base program, and extend  by convention, stating that
by convention, stating that  . Second, the projection of a product line on a subset S of its products is the product line obtained by restricting the
. Second, the projection of a product line on a subset S of its products is the product line obtained by restricting the  formula to describe only the products in S and by ignoring delta modules that are never activated. Third, the following definitions introduce auxiliary structures and getters that are useful to type check an IF\(\varDelta \)J product line.
formula to describe only the products in S and by ignoring delta modules that are never activated. Third, the following definitions introduce auxiliary structures and getters that are useful to type check an IF\(\varDelta \)J product line.
Definition 1
(FCST). A Class Signature (CS) is a class declaration deprived of the bodies of its methods, it comprises the name of the class and of its superclass, and a mapping from attribute names to types. A Family Class Signature (FCS) is a more liberal version of class signature that may extend multiple classes and associate more than one type to each attribute name. A Family Class Signature table (FCST) is a mapping that associates to each class name C an FCS for C. The subtyping relation \(<:\) described by an FCST can be cyclic. A Class Signature Table (CST) is a FCST that contains only class signatures and has an acyclic subtyping relation.
To simplify the notation, except when stated otherwise, we always assume in the following a fixed product line  . The FCST of L, denoted by
. The FCST of L, denoted by  , contains for each class C declared in AB all superclasses of C and all types of all attributes of C. Note that the FCST of L is defined only in terms of AB and it can be computed by a straightforward inspection of it. The FCST of a set of IFJ programs (or of a subset of AB) is defined similarly.
, contains for each class C declared in AB all superclasses of C and all types of all attributes of C. Note that the FCST of L is defined only in terms of AB and it can be computed by a straightforward inspection of it. The FCST of a set of IFJ programs (or of a subset of AB) is defined similarly.
Definition 2
(Getters on AB
).  is the set of modules that add the class C;
is the set of modules that add the class C;  is the set of modules that remove the class C;
is the set of modules that remove the class C;  is the set of modules that modify the class C without changing its
is the set of modules that modify the class C without changing its  clause;
clause;  is the set of modules that modify the class C also by changing its
is the set of modules that modify the class C also by changing its  clause;
clause;  is
is  ;
;  is the set of modules that add the attribute
is the set of modules that add the attribute  ;
;  is the set of modules that remove the attribute
is the set of modules that remove the attribute  ;
;  is the set of modules that modify the attribute
is the set of modules that modify the attribute  ;
;  ) is the set of modules that modify the method
) is the set of modules that modify the method  without using calls to \(\mathrm{\mathtt{original}}\) (i.e., replace its body); and
without using calls to \(\mathrm{\mathtt{original}}\) (i.e., replace its body); and  is the set of modules that modify the method
is the set of modules that modify the method  by also using calls to \(\mathrm{\mathtt{original}}\) (i.e., wrap its body).
by also using calls to \(\mathrm{\mathtt{original}}\) (i.e., wrap its body).
Definition 3
(Getter on FM and CK
). Let \(\varPhi \) be extended to include module names d as propositional variables. The formula  specifies the products and binds each variable d to the activation condition of module d (i.e., it specifies which modules are activated for each product).Footnote 1
specifies the products and binds each variable d to the activation condition of module d (i.e., it specifies which modules are activated for each product).Footnote 1
3 Two Delta-Oriented Programming Guidelines
The first guideline is to avoid useless operations, i.e., declarations in P and  or
or  in
in  that introduce code that is never present in any of the variants.
that introduce code that is never present in any of the variants.
-
G1. Ensure that the product line does not contain useless operations.
For instance, in the product line obtained by projecting the EPL on the products described by \(\lnot \textsf {fToString}\), the declarations of the methods with name toString in the base program and in the  class operation in the delta module dAdd are useless. The notion of useless operation is formalized as follows (thus making Guideline G1 automatically checkable).
class operation in the delta module dAdd are useless. The notion of useless operation is formalized as follows (thus making Guideline G1 automatically checkable).
Definition 4
(Useless operation and module). The declaration, addition or modification of an attribute  in a module d is useless iff the formula
in a module d is useless iff the formula  is valid. An
is valid. An  clause introduced in a class C by a module d is useless iff the formula
clause introduced in a class C by a module d is useless iff the formula  is valid. A module d is useless iff
is valid. A module d is useless iff  is valid.
is valid.
The second guideline is to have consistent declarations over the whole SPL (the FOP case-studies presented in [22] adhere to this guideline). For IF\(\varDelta \)J (since IFJ has no method overloading and field shadowing), this means that two declarations of the same attribute (of the same class) in two different modules must have the same type.Footnote 2 We call this property type-uniformity. It can be straightforwardly formalized by exploiting the family class signature table of the product line.
Definition 5
(Type-uniformity). A FCST FCST is type-uniform iff:
-
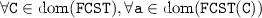 the set
the set  is a singleton; and
is a singleton; and -
 such that
such that 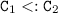 and
and  , we have:
, we have: 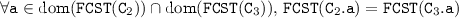
An IF\(\varDelta \)J product line (or a subset of its artifact base, or a set of IFJ programs) is type-uniform iff its FCST is type-uniform.
Our second guideline is thus stated as follows (and it can automatically be checked by a straightforward inspection of the FCST).
-
G2. Ensure that the product line is type-uniform.
The EPL is not type-uniform, because of the method eval of class Exp, that is added with two different types by delta modules dEval1 and dEval2, respectively. Instead, both its two projections respectively described by the mutually exclusive features fEval1 and fEval2 are type-uniform.
We say that an IF\(\varDelta \)J product line is variant-type-uniform to mean that: (i) its variants can be generated; and (ii) the FCST of the set of its variants is type-uniform. The following proposition illustrate how type-uniformity relates to variant-type-uniformity.
Proposition 1
Let L be an IF\(\varDelta \)J product line such that its variants can be generated. If L is type-uniform, then it is variant-type-uniform. If L satisfies Guideline G1 and is variant-type-uniform, then it is type-uniform.
4 Type Checking for Type-Uniform IF\(\varDelta \)J
This section presents a version of the type checking approach tuned to exploit Guideline G2 and states its correctness and completeness. Type-uniformity makes type checking more efficient. The approach is modularized in three independent parts: partial typing, applicability, and dependency. All the parts rely on the FCST of the product line (see Definition 1).
Product Line Partial Typing. Partial typing checks that all fields, methods and classes in AB type-check with respect to the product line FCST (i.e., with respect to declarations made in AB). Partial typing does not use any knowledge about valid feature combinations (it does not use FM and CK), so it does not guarantee that variants are well-typed, as delta modules may be activated or not. However, it guarantees that variants that have their inner dependencies satisfied (i.e., all used classes, methods and fields are declared) are well-typed.
The IF\(\varDelta \)J partial-type-system is a straightforward extension of the (standard) IFJ type system [5] that: (i) includes rules for the new syntactic constructs of IF\(\varDelta \)J; (ii) checks well-typedness with respect to the product line FCST (instead of the program CST); and (iii) allows to introduce a same class or attribute in different modules of AB (e.g., a class of name C may be added by different delta modules).
The projection of the EPL described by feature fEval1 is type-uniform. Its artifact base (which is obtained from the EPL artifact base in Fig. 1 by dropping the delta module dEval2) is accepted by partial typing, even if the method Exp.eval might not be available in some variant (in principle the delta module dEval1 might not be selected). This is because the way the method Exp.eval is used in the method Test.test in the base program is correct with respect to its definition in the delta module dEval1 (it takes no parameters and returns a Lit object).
Product Line Applicability. Applicability ensures that variants can actually be generated (variant generation fails if, e.g., a delta module that adds a class C is applied to an intermediate variant that already contains a class named C). It is formalized by a constraint ensuring that, during variant generation, each delta operation is applied to an intermediate variant on which that operation is defined. For instance, for adding a class C, this class must not be present in the intermediate variant (either it never was added, or it was removed at some point). The applicability constraint comprises three validation parts: element addition (either a class or an attribute), element removal, and element modification.
In the following we use \(\rho \) to denote either a class name C or a fully qualified attribute name  . The constraint for checking that an element \(\rho \) can be added is as follows:
. The constraint for checking that an element \(\rho \) can be added is as follows:

It ensures that all  operations are performed on a partial variant that does not contain the added element: basically, it requires that if two delta modules d and
operations are performed on a partial variant that does not contain the added element: basically, it requires that if two delta modules d and  add the same element, then there must be another delta module
add the same element, then there must be another delta module  in between that removes it.
in between that removes it.
The constraint for removal of an element \(\rho \) is slightly more complex:

In comprises two parts: the first part ( ) ensures that the element \(\rho \) is added to the partial variant (by some \(\mathtt{{d_1}}\)) before it is removed (by d); the second part ensures that if two delta modules d and
) ensures that the element \(\rho \) is added to the partial variant (by some \(\mathtt{{d_1}}\)) before it is removed (by d); the second part ensures that if two delta modules d and  remove \(\rho \), then there is another delta module \(\mathtt{{d_2}}\) in between that adds it.
remove \(\rho \), then there is another delta module \(\mathtt{{d_2}}\) in between that adds it.
The constraint for modification of an element \(\rho \) simply ensures that \(\rho \) is present for the modification:

Basically, it checks that there is a delta module  that adds the element before it is modified by d, and that there is no delta module
that adds the element before it is modified by d, and that there is no delta module  in between that removes it.
in between that removes it.
The formula  combines the constraints described above, and the formula
combines the constraints described above, and the formula  associates to each product of L its applicability constraints. Applicability-consistency (i.e., the fact that variants of L can be generated) is therefore formalized as follows.
associates to each product of L its applicability constraints. Applicability-consistency (i.e., the fact that variants of L can be generated) is therefore formalized as follows.
Definition 6
(Applicability-consistency). A product line L is applicability-consistent iff the formula  is valid.
is valid.
Product Line Dependency. Dependency ensures that no generated variant has a missing dependency, which can be straightforwardly expressed by means of constraints on attributes and classes. For instance, the dependencies induced by “class C extends class  ” could be encoded with the constraint
” could be encoded with the constraint  , as the declaration of C requires that the declaration of
, as the declaration of C requires that the declaration of  is present and that
is present and that  is not a subtype of C (to ensure that the inheritance graph has no loops). In DOP, since each declaration is made in a module that can be activated or not, dependency constraints must be lifted at the module level. For instance, if the fact that C extends
is not a subtype of C (to ensure that the inheritance graph has no loops). In DOP, since each declaration is made in a module that can be activated or not, dependency constraints must be lifted at the module level. For instance, if the fact that C extends  is declared in the module d, then the previous constraint becomes:
is declared in the module d, then the previous constraint becomes:  , basically stating that if the module d is activated and no other module that removes C or changes its
, basically stating that if the module d is activated and no other module that removes C or changes its  clause is activated afterward, then the class
clause is activated afterward, then the class  must be present in the generated variant and must not be a subtype of C.
must be present in the generated variant and must not be a subtype of C.
The product line dependency constraint is generated by exploiting the rules in Figs. 3 and 4, which infer a dependency constraint for each expression and declaration, respectively. It is based on the following atomic constraints:  (resp.
(resp.  ) ensures that the class C (resp. attribute
) ensures that the class C (resp. attribute  ) added by the delta module d will be removed afterward;
) added by the delta module d will be removed afterward;  ensures that the class C added or modified by the delta module d will have its
ensures that the class C added or modified by the delta module d will have its  clause modified by another delta module afterward;
clause modified by another delta module afterward;  ensures that the method
ensures that the method  added or modified by the delta module d will be replaced by another delta module afterward;
added or modified by the delta module d will be replaced by another delta module afterward;  ensures that T (either a class or
ensures that T (either a class or  ) is a subtype of
) is a subtype of  ;
;  (resp.
(resp.  ) ensures that the class C (resp. the attribute a) is present in the generated variant (resp. is an attribute of the class C, possibly through inheritance).
) ensures that the class C (resp. the attribute a) is present in the generated variant (resp. is an attribute of the class C, possibly through inheritance).
Dependency generation rules for expressions perform a type analysis to know what is the type of each expression, which is used to compute the appropriate dependency. They have judgments of the form  , where: \(\varGamma \) is an environment giving the type of each variable; e is the parsed expression; T is its type; and \(\varPhi \) is the generated dependency constraint. The rules for expressions are quite direct: accessing a variable (rule (E:Var)) does not raise any dependency, while accessing a field requires for this field to be accessible (rule (E:Field)); method calls (rule (E:Meth)) require that the method is accessible and that the parameters have a type consistent with the method’s declaration; object creation requires for the class of the object to be defined (rule (E:New)); and
, where: \(\varGamma \) is an environment giving the type of each variable; e is the parsed expression; T is its type; and \(\varPhi \) is the generated dependency constraint. The rules for expressions are quite direct: accessing a variable (rule (E:Var)) does not raise any dependency, while accessing a field requires for this field to be accessible (rule (E:Field)); method calls (rule (E:Meth)) require that the method is accessible and that the parameters have a type consistent with the method’s declaration; object creation requires for the class of the object to be defined (rule (E:New)); and  does not raise any dependency (rule (E:Null)), while casting and assignment generate constraints ensuring that the right inheritance relation holds (rules (E:Cast) and (E:Assign)).
does not raise any dependency (rule (E:Null)), while casting and assignment generate constraints ensuring that the right inheritance relation holds (rules (E:Cast) and (E:Assign)).
Dependency generation rules for declarations have judgments of the form \(\varOmega \vdash A\mathrel {:}\varPhi \) where \(\varOmega \) can either be empty, d (meaning that we are parsing the content of the module d), or  (meaning that we are parsing the content of the class C inside d); A is the parsed declaration (e.g., an attribute, a class operation); and \(\varPhi \) is the generated constraint. Rules (D:Field) for field and (D:Meth) for method declarations are quite direct: if the attribute is not removed afterward, the dependencies it generates must be validated. The rule (D:Class) for class declaration is similar (if the class is not removed, its inner dependencies must be validated), with an additional clause for the
(meaning that we are parsing the content of the class C inside d); A is the parsed declaration (e.g., an attribute, a class operation); and \(\varPhi \) is the generated constraint. Rules (D:Field) for field and (D:Meth) for method declarations are quite direct: if the attribute is not removed afterward, the dependencies it generates must be validated. The rule (D:Class) for class declaration is similar (if the class is not removed, its inner dependencies must be validated), with an additional clause for the  clauses (as previously discussed). Rules (D:ModMD) for modifying methods and (D:AddAtt) and (D:AddClass) for adding attributes and classes simply forward the constraints generated from the inner declaration, while removing an attribute or a class (rules (D:RmAtt) and (D:RmClass)) does not generate any dependency. The rules (D:AddClass1) and (D:AddClass2) for modifying a class are simple variations on the rule for class declaration. Finally, the dependencies of a delta module body are activated only if the delta module is activated (rule (D:Delta)), and the dependencies of a whole program is the conjunction of the dependencies of all its parts (rule (D:P)). The resulting constraint thus has the form
clauses (as previously discussed). Rules (D:ModMD) for modifying methods and (D:AddAtt) and (D:AddClass) for adding attributes and classes simply forward the constraints generated from the inner declaration, while removing an attribute or a class (rules (D:RmAtt) and (D:RmClass)) does not generate any dependency. The rules (D:AddClass1) and (D:AddClass2) for modifying a class are simple variations on the rule for class declaration. Finally, the dependencies of a delta module body are activated only if the delta module is activated (rule (D:Delta)), and the dependencies of a whole program is the conjunction of the dependencies of all its parts (rule (D:P)). The resulting constraint thus has the form  , giving for all module
, giving for all module  its dependencies \(\varPhi _i\). Let then
its dependencies \(\varPhi _i\). Let then  be the constraint generated for the product line L. The formula
be the constraint generated for the product line L. The formula  associates to each product of L its dependency constraints. Dependency-consistency (i.e., variants of L have all their dependencies fulfilled) is therefore formalized as follows.
associates to each product of L its dependency constraints. Dependency-consistency (i.e., variants of L have all their dependencies fulfilled) is therefore formalized as follows.
Definition 7
(Dependency-consistency). A product line L is dependency-consistent iff the formula  is valid.
is valid.
Correctness and Completeness of the Approach. The following theorem states that, if the product line follows Guideline G2, then the presented IF\(\varDelta \)J product line type checking approach is correct with respect to generating variants and checking them using the IFJ type system. The approach is complete (i.e., if the check performed by the approach fails then at least one variant is not a well-typed IFJ program) if also Guideline G1 is followed.
Theorem 1
Let L be a type-uniform product line. Consider the properties:
-
i.
L is well partially-typed, applicability- and dependency-consistent.
-
ii.
Variants of L can be generated and are well-typed IFJ programs.
Then: (i) implies (ii); and if L has no useless operations then (ii) implies (i).
5 Type Checking for IF\(\varDelta \)J Without Guidelines
In this section we outline how the type checking approach presented in Sect. 4 can be tuned to non type-uniform product lines (i.e., not to exploit any guidelines). This modification is quite straightforward, although it involves many technical details. Partial typing must be adapted since the product line FCST maps attribute names to sets of types with possibly more than one element, and expressions can have more than one type. E.g., a method call expression  can use any declaration of the method
can use any declaration of the method  (considering that e is typed C) whose type accepts a combination of types of the call’s arguments. So partial typing may carry a combinatorial explosion.
(considering that e is typed C) whose type accepts a combination of types of the call’s arguments. So partial typing may carry a combinatorial explosion.
Applicability does not need any modification to analyze non-uniform programs. This is due to the fact that the applicability criteria focuses on the interplay between delta operations and do not consider attribute types.
Dependency is the part that changes more: it now has to be type-aware, and thus subsumes partial typing. We illustrate it on the rule that generates the dependency for field usage (second rule in Fig. 3). This rule must be extended in two ways to manage non-uniform programs: (i) e can have more than one type; (ii) the field type lookup  can return different possible types for
can return different possible types for  , depending on which modules are activated. Consequently, the dependency generation judgment for expressions now has the form
, depending on which modules are activated. Consequently, the dependency generation judgment for expressions now has the form  where \({T_{i}}\) are the possible types of e, and \(\varPhi _i\) is the condition (i.e. which module must or must not be activated) for e to have the type \({T_{i}}\) in the final product.
where \({T_{i}}\) are the possible types of e, and \(\varPhi _i\) is the condition (i.e. which module must or must not be activated) for e to have the type \({T_{i}}\) in the final product.

Hence, the rule becomes as displayed on the right, where \(\varPhi _{i,j}\) is the formula that enforces that the field \({\texttt {f}}\) accessible from the class \(\mathtt{{C_{i}}}\) has the type \(\mathtt{{C_{i,j}}}\) in the final product.
Correctness and completeness are stated as in Theorem 1 by dropping the assumption that the product line is type-uniform.
6 Three Other Guidelines
Our type-checking approach is modularized in three parts: (i) partial typing performs a preliminary type analysis that can be exploited by an IDE for prompt notification of type-errors and auto-completing code; (ii) applicability ensures that variants can be generated; and (iii) dependency completes the analysis done by the partial typing. The approach is tunable to exploit DOP guidelines that enforce structural regularities in product line implementation. In Sect. 4 we have presented a version tuned to exploit type-uniformity. In this section we briefly discuss three other automatically checkable guidelines (other useful guidelines could be devised).
First, whenever it is possible to enforce the following guideline (satisfied by the EPL), the dependency analysis can be simplified, as it is no longer needed to check the absence of inheritance loop in the generated variant (cf. dependency generation for class declaration and modification in Fig. 4).
-
G3. Ensure that the product line FCST subtyping relation is acyclic.
If a product line cannot be made variant-type-uniform, then guideline G2 cannot be enforced (see Proposition 1), and understanding the structure of the SPL may become an issue. The following guideline (satisfied by the EPL) aims at helping the understanding of an SPL implementation by decoupling the sources of non type-uniformity.
-
G4. Ensure that, for all distinct modules \(\mathtt{{d_1}}\) and \(\mathtt{{d_2}}\), if the set comprising \(\mathtt{{d_1}}\) and \(\mathtt{{d_2}}\) is not type-uniform then their activation conditions are mutually exclusive.
Consider for instance a module d that declares an attribute  with a type t. Then, if the SPL follows G3, we are sure that each variant using d in its construction will have
with a type t. Then, if the SPL follows G3, we are sure that each variant using d in its construction will have  typed t when it contains this attribute.
typed t when it contains this attribute.
We introduce our final guideline with the following consideration: implementing or modifying a product line involves editions of the feature model, the configuration knowledge and the artifact base that may affect only a subset of the products. For example, adding, removing or modifying a delta module d and its activation condition will affect only the products that activate d. Therefore, only the projection of the product line on the affected products needs to be re-analyzed. If such a projection is type-uniform, then the more efficient type checking technique of Sect. 4 can be used (even if the whole product line is not type-uniform). The following guideline naturally arises.
-
G5. (i) Ensure that the set of products is partitioned in such a way that: each part S is type-uniform (i.e., the projection of the SPL on S is type uniform), and the union of any two distinct parts is not type-uniform.
(ii) If the number of parts of such a partition is “too big”, then merge some of them to obtain a “small enough” partition where only one part is not type-uniform.
The goal of this guideline is to allow to use as much as possible the version of the approach presented in Sect. 4. For the EPL the partition that satisfies Guideline G5.i is unique: the two products with feature fEval1 and the four products with feature fEval2. However, in general, such a partition may be not unique and tool support for identifying a partition that satisfies G5.i and further conditions (e.g., having a minimal number of parts) or G5.ii and other conditions (e.g., the number of products in the non type-uniform part is as small as possible) would be valuable.
7 Related Work
Product line analysis approaches can be classified into three main categories [23]: Product-based analyses operate only on generated variants (or models of variants); Family-based analyses operate only on the AB by exploiting the FM and the CK to obtain results about all variants; Feature-based analyses operate on the building blocks of the different variants (feature modules in FOP and delta modules in DOP) in isolation (without using the FM and the CK) to derive results on all variants. We refer to [23] for a survey on product line type checking. Here we discuss previous type checking approaches for DOP [5, 8] and the two approaches for FOP that are closets to our proposal [9, 22].
The type checking approach for DOP in [5] comprises: a feature-based analysis that uses a constraint-based type system for IFJ to infer a type abstraction for each delta module; and a product-based step that uses these type abstractions to generate, for each product of the SPL, a type abstraction (of the associated variant) that is checked to establish whether the associated variant type checks. The approach of [5] is enhanced in [8] by introducing a family-based step that builds a product family generation tree which is then traversed in order to perform optimized generation and check of type abstractions of all variants. The approach proposed in this paper, which is feature-family-based, represents an achievement over [5, 8] since it does not require to iterate over the set of products (cf. Sect. 1) and supports earlier detection of errors via partial typing.
The paper [22] informally illustrates the implementation of a family-based approach for the AHEAD system [4]. The approach comprises: (i) a family-feature-based step that computes for each class a stub (all stubs can be understood as a type-uniform FCST for the product line) and compiles each feature module in the context of all stubs (thus performing checks corresponding to our type-uniformity and partial-typing); and (ii) a family-based step that infers a set of constraints that are combined with the FM to generate a formula (corresponding to our type-uniform applicability and dependency) whose satisfiability should imply that all variants successfully compile.
The paper [9] formalizes a feature-family-based approach for the Lightweight Feature Java (LFJ) calculus, which models FOP for the Lightweight Java (LJ) [21] calculus. The approach comprises: (i) a feature-based step that uses a constraint-based type system for LFJ to analyze each feature module in isolation and infer a set of constraints for each feature module; and (ii) a family-based step where the FM and the previously inferred constraints are used to generate a formula whose satisfiability implies that all variants type check. The applicability and dependency analyses presented in Sect. 5 provide an extension to DOP of these two steps. Moreover, our approach provides partial typing for early error detection and is tunable to exploit different programming guidelines.
8 Conclusions and Future Work
We have proposed a modular and tunable approach for type checking DOP product lines. A prototypical implementation is available [2] (currently only the version of the approach exploiting type-uniformity is supported).
In future work we plan to: implement our approach for both DeltaJ 1.5 [14] (a prototypical implementation of DOP that supports full Java 1.5) and ABS [12] (this would allow experimental comparison with the approaches of [5, 8], which have been implemented for ABS [1]); to develop case studies to evaluate the effectiveness of the approach and of the proposed guidelines; to investigate further DOP guidelines; and to develop tool support to allow the programmer to choose the guidelines to be automatically enforced. We also plan to investigate whether the proposed DOP guidelines (or other guidelines) could be useful for other kind of product line analyses. In particular, we would like to consider formal verification (proof systems for the verification of DOP product lines of Java programs have been recently proposed [7, 10]).
Notes
- 1.
The last occurrence of d in
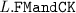 is not used as a variable: it is used as argument of the map
is not used as a variable: it is used as argument of the map 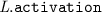 to obtain the activation condition of module d.
to obtain the activation condition of module d. - 2.
Note that, since the type system of IFJ is nominal, a class may have different sets of attributes in different variants.
References
https://github.com/abstools/abstools/tree/master/frontend/src/abs/frontend/delta
Batory, D.: Feature models, grammars, and propositional formulas. In: Obbink, H., Pohl, K. (eds.) SPLC 2005. LNCS, vol. 3714, pp. 7–20. Springer, Heidelberg (2005)
Batory, D., Sarvela, J.N., Rauschmayer, A.: Scaling step-wise refinement. In: 2003 Proceedings of ICSE, pp. 187–197. IEEE (2003)
Bettini, L., Damiani, F., Schaefer, I.: Compositional type checking of delta-oriented software product lines. Acta Informatica 50(2), 77–122 (2013)
Clements, P., Northrop, L.: Software Product Lines: Practices and Patterns. Addison Wesley Longman, Boston (2001)
Damiani, F., Owe, O., Dovland, J., Schaefer, I., Johnsen, E.B., Yu, I.C.: A transformational proof system for delta-oriented programming. In: 2012 Proceedings of SPLC, vol. 2, pp. 53–60. ACM (2012)
Damiani, F., Schaefer, I.: Family-based analysis of type safety for delta-oriented software product lines. In: Margaria, T., Steffen, B. (eds.) ISoLA 2012, Part I. LNCS, vol. 7609, pp. 193–207. Springer, Heidelberg (2012)
Delaware, B., Cook, W.R., Batory, D.: Fitting the pieces together: a machine-checked model of safe composition. In: 2009 Proceedings of ESEC/FSE. ACM (2009)
Hähnle, R., Schaefer, I.: A Liskov principle for delta-oriented programming. In: Margaria, T., Steffen, B. (eds.) ISoLA 2012, Part I. LNCS, vol. 7609, pp. 32–46. Springer, Heidelberg (2012)
Igarashi, A., Pierce, B., Wadler, P.: Featherweight Java: a minimal core calculus for Java and GJ. ACM TOPLAS 23(3), 396–450 (2001)
Johnsen, E.B., Hähnle, R., Schäfer, J., Schlatte, R., Steffen, M.: ABS: a core language for abstract behavioral specification. In: Aichernig, B.K., Boer, F.S., Bonsangue, M.M. (eds.) Formal Methods for Components and Objects. LNCS, vol. 6957, pp. 142–164. Springer, Heidelberg (2011)
Kästner, C., Apel, S., ur Rahman, S.S., Rosenmüller, M., Batory, D., Saake, G.: On the impact of the optional feature problem: analysis and case studies. In: Proceedings of SPLC 2009, pp. 181–190 (2009)
Koscielny, J., Holthusen, S., Schaefer, I., Schulze, S., Bettini, L., Damiani, F.: Deltaj 1.5: delta-oriented programming for Java 1.5. In: 2014 Proceedings of PPPJ, pp. 63–74. ACM (2014)
Krueger, C.: Eliminating the adoption barrier. IEEE Softw. 19(4), 29–31 (2002)
Lienhardt, M., Clarke, D.: Conflict detection in delta-oriented programming. In: Margaria, T., Steffen, B. (eds.) ISoLA 2012, Part I. LNCS, vol. 7609, pp. 178–192. Springer, Heidelberg (2012)
Lopez-Herrejon, R.E., Batory, D., Cook, W.: Evaluating support for features in advanced modularization technologies. In: Gao, X.-X. (ed.) ECOOP 2005. LNCS, vol. 3586, pp. 169–194. Springer, Heidelberg (2005)
Schaefer, I.: Proceedings of VaMoS 2010. In: International Workshop on Variability Modelling of Software-intensive Systems (2010)
Schaefer, I., Bettini, L., Bono, V., Damiani, F., Tanzarella, N.: Delta-oriented programming of software product lines. In: Bosch, J., Lee, J. (eds.) SPLC 2010. LNCS, vol. 6287, pp. 77–91. Springer, Heidelberg (2010)
Schaefer, I., Damiani, F.: Pure delta-oriented programming. In: 2010 Proceedings of FOSD, pp. 49–56. ACM (2010)
Strniša, R., Sewell, P., Parkinson, M.: The Java module system: core design and semantic definition. In: 2007 Proceedings of OOPSLA, pp. 499–514. ACM (2007)
Thaker, S., Batory, D., Kitchin, D., Cook, W.: Safe composition of product lines. In: Proceedings of GPCE 2007, pp. 95–104. ACM (2007)
Thüm, T., Apel, S., Kästner, C., Schaefer, I., Saake, G.: A classification and survey of analysis strategies for software product lines. ACM Comput. Surv. 47(1), 6:1–6:45 (2014)
Acknowledgements
We are grateful to Don Batory for clarifications about previous work on type checking FOP, and to Ina Schaefer and Thomas Thüm for discussions about how to classify SPL type checking approaches. We also thank the iFM 2016 anonymous reviewers for insightful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
Damiani, F., Lienhardt, M. (2016). On Type Checking Delta-Oriented Product Lines. In: Ábrahám, E., Huisman, M. (eds) Integrated Formal Methods. IFM 2016. Lecture Notes in Computer Science(), vol 9681. Springer, Cham. https://doi.org/10.1007/978-3-319-33693-0_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-33693-0_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-33692-3
Online ISBN: 978-3-319-33693-0
eBook Packages: Computer ScienceComputer Science (R0)




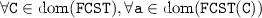 the set
the set  is a singleton; and
is a singleton; and such that
such that 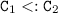 and
and  , we have:
, we have: 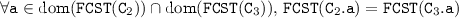


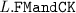 is not used as a variable: it is used as argument of the map
is not used as a variable: it is used as argument of the map 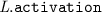 to obtain the activation condition of module
to obtain the activation condition of module