Keywords

1 Introduction

Microsoft Kinect is a representative RGB-D sensor that has achieved great success in a wide variety of vision related applications such as augmented reality, robotics, and human-computer interactions. The performance of these applications largely depends on the quality of acquired depth images. It has been observed that Kinect depth maps suffer from various defects, including holes, wrong or inaccurate depth measurements, and interference noise. Because the depth information is unavailable in holes and depth discontinuities between objects should be preserved, the recovery of Kinect depth maps has become a challenging problem.

Qi et al. [1] proposed a fusion based method using non-local filtering scheme for restoring depth maps. He et al. [2] proposed a guided filter that can preserve sharp edge and avoid reversal artifacts when smoothing a depth map. Dakkak et al. [3] proposed an iterative diffusion method which utilizes both available depth values and color segmentation results to recover missing depth information, but the results are sensitive to the segmentation accuracy. In order to obtain more precise filter coefficients, Camplani et al. [4] used a joint bilateral filter to calculate the weights of available depth pixels according to collocated pixels in color image. Based on a joint histogram, Min et al. [5] instead proposed a weighted mode filter to prevent the output depth values from being blurred on the depth boundaries. However, filtering-based approaches often yield poor results near the depth discontinuities, especially around the large holes.

Inpainting techniques seem more promising in depth hole filling than filtering, interpolation and extrapolation algorithms. With an aligned color image, Liu et al. [6] proposed an extended FMM approach [7] to guide depth inpainting. Structure-based inpainting [8] fills the holes by propagating structure into the target regions via diffusion. The diffusion process makes holes blurred, and texture is thus lost. Xu et al. [9] further introduced the exemplar-based texture synthesis into structure propagation so that the blurring effects can be somewhat avoided. In order to prevent edge fatting or shrinking after hole inpainting, Miao et al. [10] used the fluctuating edge region in depth map to assist hole completion. However, the missing depth values near the object contour are directly assigned to the mean of available depth values in fluctuating edge region, which is hence inaccurate for representing the depth contours.

Reconstruction-based methods apply image synthesis techniques to predict missing depth values. Since the reconstruction coefficients are resolved in a closed-loop scheme in terms of the minimization of residuals, higher hole-filling accuracy is achievable. Chen et al. [11, 12] cast the depth recovery as an energy minimization problem, which addresses the depth hole filling and denoising simultaneously. Yang et al. [13] proposed an adaptive color-guided autoregressive (AR) model for high quality depth recovery, where the depth recovery task is converted into a minimization of AR prediction errors subject to measurement consistency.

Based on sparse representation, in this paper, we represent missing depth regions as the linear combination of the surrounding available depth values, and establish a similarity and position constrained sparse representation (SPSR) to solve the optimal weights with the help of the associated color image. SPSR comprises similarity-distance-inducing weighted ℓ1 sparsity penalty term and position-inducing weighted data-fidelity term, which thus not only readily grasps the salient features of depth image but also considerably promotes representation accuracy.

2 Proposed Method

2.1 Problem Setup

In reconstruction-based methods, the missing depth value is recovered from the surrounding available pixels around the target by a linear weighted combination representation. Let D(x) denote the missing depth at position x and {D(y m ) | 1 ≤ m ≤ M} denote all M known depth pixels at positions {y m  | 1 ≤ m ≤ M} in a search window centered at x. This procedure reads

$$ D(x) = \sum\limits_{m = 1}^{M} {w(y_{m} )D(y_{m} )} $$
(1)

where w(y m ) is the coefficient of D(y m ), reflecting the contribution of the available depth value at position y m to the reconstruction. The key issue for successfully reconstructing D(x) is to appropriately determine predictor coefficients.

Reconstruction coefficients are usually assigned by how similar surrounding pixels are to the target pixel. Gaussian smoothing filter, bilateral filter [14] and non-local means (NLM) [15] is able to obtain the coefficients.

However, the coefficients by the above mentioned methods are primarily responsible for the distance or similarity between the nearby pixels and the target pixel, but neglect the data fidelity in terms of the reconstruction error. In contrast, linear regression method can resolve the coefficients by minimizing the error between reconstructed data and observed data, whose solution is hence theoretically deduced rather than intuitively assigned. Furthermore, since the lost depth pixels cannot provide a valid observation, the objective of the linear regression is usually established on the basis of the color image instead of the depth map.

Fig. 1.
figure 1

Outline of the analysis and synthesis framework in hole filling. Notations “I” and “D” mean the color intensity of a certain patch and the depth of a certain pixel, respectively.

Full size image

2.2 Similarity and Position Constrained Sparse Representation

In formulating the objective regression function, if only the target pixel is represented as a linear combination of surrounding pixels, the equation is too much under-determined and is thus hard to address. Inspired by the NLM, we instead perform a patch-wise regression analysis. Patches are centered on the target pixel to be recovered, where all pixels instead of the single centroid pixel attend the regression.

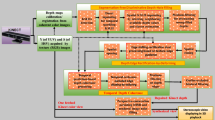
Figure 1 illustrates the outline of our used framework, which consists of two major phases: analysis phase and synthesis phase. The former fulfills patch-wise regression analysis to obtain the linear combination coefficients in color space, and then the latter reconstructs the missing counterpart depth with the available coefficients. To ensure that the synthesis phase uses valid reference depth values, the corresponding depth pixel of the centroid pixel in a reference patch should not be located at holes.

Let \( {\mathbf{x}} \in R^{N \times 1} \) be an observed patch, stacked into a N-dimensional column vector, and \( {\mathbf{Y}} \in R^{N \times M} \) be a training set being composed of M nearby reference patches in a window, whose m-th column consists of an individual reference patch \( {\mathbf{Y}}_{m} \). Without loss of generality, the regularized linear regression reads:

$$ {\mathbf{w}}^{ * } {\kern 1pt} = \mathop {\arg \hbox{min} }\limits_{{{\kern 1pt} {\mathbf{w}}}} \left\{ {\left\|{\mathbf{x}} - {\mathbf{Yw}}\right\|_{2}^{2} {\kern 1pt} {\kern 1pt} + \lambda\Omega ({\mathbf{w}})} \right\}{\kern 1pt} $$
(2)

where \( {\mathbf{w}} \in R^{M \times 1} \) is an unknown coefficient vector, whose entries \( {\mathbf{w}}_{i} ,{\kern 1pt} {\kern 1pt} i = 1,2, \ldots ,M \) is associated with an individual basis in training set. \( \left\|{\mathbf{x}} - {\mathbf{Yw}}\right\|_{2}^{2} {\kern 1pt} \) is the so-called data-fidelity term, representing regression error (fitting error), and \( \Omega ({\mathbf{w}}) \) is a prior related penalty term. Typically, \( \Omega ({\mathbf{w}}) = \left\| {\mathbf{w}} \right\|_{1} \), corresponding to ℓ 1 norm sparse representation; or \( \Omega ({\mathbf{w}}) = \left\|{\mathbf{w}}\right\|_{2}^{2} {\kern 1pt} {\kern 1pt} \), corresponding to squared ℓ 2 norm ridge regression. The penalty term in the form of ℓ 1 norm or squared ℓ 2 norm promotes sparsity or smoothness of solution, respectively. Parameter λ ≥ 0 is an appropriately chosen regularization factor, tuning the tradeoff between the regression error and the penalization.

In a deep insight, the pixels belonging the same object nearly share equal depth values, while pixels located in different objects often give quite distinct depth values. From the perspective of the reconstruction of missing depth values, the surrounding candidates in the same object should own larger weights than others. Thus, the reconstruction coefficients of depth maps are sparse in nature. In fact, sparsity priors have been extensively exploited in previous works [16–18], which approach the problem of depth inference by including a sparsity prior on local depth features. Therefore, we cast the reconstruction of lost depth values as a sparsity representation problem, thus efficiently charactering the saliency of depth maps and adapting to the structure of depth signals.

Bilateral filter considers spatial distance and intensity similarity in constructing coefficients, yet irrespective of prediction residuals. Regression analysis, on the contrary, considers fitting error, but completely ignores geometric distance and similarity. To make full use of the advantages offered by bilateral filter and regression analysis, we intend to incorporate the metrics of distance and similarity into the regularized objective function. Following this idea, one possible approach is to impose constraints onto the weight penalty term. In this paper, we take ℓ 1 norm SR and its weighted variant on penalty term is expressed as:

$$ {\mathbf{w}}^{ * } {\kern 1pt} = \mathop {\arg \hbox{min} }\limits_{{\mathbf{w}}} \left\{ {\left\|{\mathbf{x}} - {\mathbf{Yw}}\right\|_{2}^{2} {\kern 1pt} {\kern 1pt} + \lambda \left\| {{\mathbf{h}} \circ {\mathbf{w}}} \right\|_{1} } \right\} $$
(3)

where “\( \circ \)” denotes element-wise vector product and h is the weights preferring the desirable properties of sparse solution w. Obviously, the large entries of h will result in small entries of w. Therefore, if we specify h by the product of spatial distance and intensity similarity, i.e., \( {\mathbf{h}} = {\mathbf{d}} \circ {\mathbf{s}} \), then the reference patches being close and similar to the target patch will be expected to take large coefficients. To be more precise, spatial distance d is patch-wisely calculated by the Euclidean measure of the centroid coordinates of target and reference patches. Suppose the target patch locates at (i, j) and the m-th reference one locates at (k, l), then the m-th entry of d given by:

$$ {\mathbf{d}}_{m} = \sqrt {(i - k)^{2} + (j - l)^{2} } $$
(4)

Intensity similarity s is obtained in terms of the Euclidean measure of the pixel values in target patch and individual reference one:

$$ {\mathbf{s}}_{m} = \left\|{\mathbf{x}} - {\mathbf{Y}}_{m} \right\|_{2} $$
(5)

As illustrated in Fig. 1, although the coefficients are obtained for a whole patch centered at the target color pixel, yet they are only applied to the reconstruction of the centroid depth pixel rather than all pixels in a depth patch. Therefore, the centroid target pixel should be given higher priority than other ones in computing the regression error. In other words, the errors of centroid pixels in a patch should be overestimated while those of the faraway pixels from patch center should be underestimated. If we use weighting on errors to serve this purpose, the centroid pixels should be assigned larger weights than others. Alternatively, the weights should be in inverse proportion to the spatial intervals of the pixels to the centroid one. As usually done, weights derived from Gaussian kernel function with respect to distance could be a better choice. Let p denote the relative positions (in Euclidean distance) of any pixels to the centroid one, then the weights read:

$$ {\mathbf{k}} = \exp ( - \frac{{{\mathbf{p}}^{2} }}{{2\sigma^{2} }}) $$
(6)

where \( \sigma \) is the decay of the exponential function. Obviously, the centroid pixel owns the largest weight, namely, 1.

Incorporating the position weights k into the error term in Eq. (3), we have a reformulated equation as follows:

$$ {\mathbf{w}}^{ * } {\kern 1pt} = \mathop {\arg \hbox{min} }\limits_{{\mathbf{w}}} \left\{ {\left\|{\mathbf{k}} \circ ({\mathbf{x}} - {\mathbf{Yw)}}\right\|_{2}^{2} {\kern 1pt} {\kern 1pt} + \lambda \left\| {{\mathbf{h}} \circ {\mathbf{w}}} \right\|_{1} } \right\} $$
(7)

which considers the spatial distance and similarity constraints on coefficients via weighting penalty term, and the position constraint on regression errors via weighting data-fidelity term.

Let K and H be diagonal weighting matrices with diagonal elements respectively being k and h and elsewhere being zeros. Equation (7) can be rewritten as:

$$ {\mathbf{w}}^{ * } {\kern 1pt} = \mathop {\arg \hbox{min} }\limits_{{\mathbf{w}}} \left\{ {\left\|{\mathbf{K}}({\mathbf{x}} - {\mathbf{Yw)}}\right\|_{2}^{2} {\kern 1pt} {\kern 1pt} + \lambda \left\| {{\mathbf{Hw}}} \right\|_{1} } \right\} $$
(8)

\( \left\|{\mathbf{Hw}}\right\|_{1} \) is actually the weighted variant of ℓ 1 norm. Let \( {\mathbf{w}}^{'} = \text{H}{\mathbf{w}} \), and thus \( {\mathbf{w}}{\kern 1pt} = {\mathbf{H}}^{ - 1} {\mathbf{w}}^{'} \), Eq. (8) can be turned into:

$$ {\mathbf{w}}^{ * } {\kern 1pt} = \mathop {\arg \hbox{min} }\limits_{{\mathbf{w}}} \left\{ {\left\|{\mathbf{K}}({\mathbf{x}} - {\mathbf{YH}}^{ - 1} {\mathbf{w}}^{'} {\mathbf{)}}\right\|_{2}^{2} {\kern 1pt} {\kern 1pt} + \lambda \left\| {{\mathbf{w}}^{'} } \right\|_{1} } \right\} $$
(9)

which can then be conveniently solved using the popular ℓ 1 norm SR numerical algorithms. Reconstruction weights are firstly solved with Eq. (9) in the associated color image and are then used to synthesize the missing depth values with Eq. (1).

3 Experiments and Results

In this section, we conduct experiments to evaluate the overall performance of the proposed algorithm. The experimental datasets contain real-world Kinect depths acquired by ourselves in door and public datasets from Middlebury RGB-D database [19], which are respectively used for qualitative and quantitative evaluations. The captured Kinect images are in a resolution of 480 × 640 while Middlebury datasets enjoy a bit bigger size of 555 × 660. Three representative state-of-the-art methods, such as Camplani’s joint bilateral filtering (JBF) [4], Liu’s color-guided FMM inpainting (GFI) [6], and Yang’s adaptive autoregressive reconstruction (AAR) [13], are used for comparisons on behalf of filter-based, inpainting-based and reconstruction-based methods, respectively. For parameter settings, our method sets the size of search window to 21 × 21, the size of patch to 5 × 5, and parameter λ to 0.1. The individual parameters in other methods are tuned to their best results according to [4, 6, 13].

3.1 Experiments on Real-World Kinect Depth Maps

In this subsection, our proposed similarity and position constrained ℓ1 sparse representation is compared with the existing three methods: Camplani’s JBF [4], Liu’s GFI [6] and Yang’s AAR [13]. To obtain real-world experimental samples, we captured indoor images under normal lighting conditions using Kinect. Because of lack of ground truth, we can only evaluate subjective effects. Two randomly selected results are shown in Figs. 2 and 4.

Fig. 2.
figure 2

Recovered results by different methods. (a) Color image; (b) Original depth map; (c) JBF; (d) GFI; (e) AAR; (f) Our method. (Color figure online)

Full size image

As we can see from the recovered depth maps in Fig. 2, our method produces more reasonable recovery than anchors around the depth boundaries. Particularly, as shown in the highlighted regions, either JBF or GFI mistakes the holes between fingers in palm and incorrectly fills in them with the foreground depth values. To observe the differences more clearly, a local magnification version of the depth map in the highlighted palm region is shown in Fig. 3. As shown in the highlighted regions, either JBF or GFI mistakes the holes between fingers in palm and incorrectly fills in them with foreground depth values. AAR gives closer outcomes to our method since they are both based on reconstruction. Figure 4 shows an example where some large holes fail to be filled in due to sharp depth discontinuities, but our method produces relatively more adequate completion of the holes than anchors.

Fig. 3.
figure 3

A detailed comparison of marked palm area in Fig. 2. (a) Color image; (b) Original depth map; (c) JBF; (d) GFI; (e) AAR; (f) Our method. (Color figure online)

Full size image
Fig. 4.
figure 4

Recovered results by different methods where some regions fail to be filled. (a) Color image; (b) Original depth map; (c) JBF; (d) GFI; (e) AAR; (f) Our method. (Color figure online)

Full size image

3.2 Experiments on Synthetically Degraded Datasets

In this subsection, we conduct another experiment on public datasets to comprehensively evaluate the performance of our method. In quantitative experiments, ground truth depth maps are needed to compute objective metrics, such as PSNR and SSIM (structural similarity measure). Reference [13] supplies the synthetic datasets with Kinect-like degradations from Middlebury’s benchmark [19], where structural missing is created along depth discontinuities and random missing is generated in flat areas. We randomly select three groups for evaluations, referred to as Art and Book, with each consisting of a triple: a color image, an original depth map (as the ground truth), and an artificially degraded depth. Figure 5 shows the color images, degraded depths and recovered results by four methods. The quantitative results are then calculated against the ground truth and are tabulated in Table 1.

Fig. 5.
figure 5

Subjective results of different methods on Middlebury datasets with synthetic degradations. (a) Color image; (b) Degraded depth map; (c) JBF; (d) GFI; (e) AAR; (f) Our method. (Color figure online)

Full size image

By a brief examination, all methods provide fine recovery performance for random missing in flat regions, and their differences mainly lie in the sharp discontinuities within missing areas. JBF and GFI produce annoying jaggy artifacts around depth discontinuities, particularly, at the side edge of the pot and the top edge of the book. But he results of our method and AAR turns out much more natural. Meanwhile, subjective performance variations roughly agree with statistics of the results reported in Table 1. In a more bit careful inspection, the objective measures in Table 1 show that our method outperforms AAR. This can be mainly attributed to the fact our method produces more optimal reconstruction weights due to imposed similarity and position constraints. Again, our method results in the best outcomes among four methods in the quantitative evaluation.

Table 1. Quantitative results of different methods on datasets with synthetic degradations.
Full size table

4 Conclusions

This paper has presented a similarity and position constrained sparse representation method for filling in holes in the Kinect depth map. With the assistance of complementary color image, the constraints of intensity similarity and spatial distance between reference patches and target one are imposed on ℓ1 sparsity penalty term and the position constraint of centroid pixel in the target patch is incorporated into data-fidelity term. In contrast to standard sparse representation and squared ℓ2 norm ridge regression, the developed sparse representation variant considering such similarity and position constraints can provide more accurate coefficients to reliably predict lost depth pixels at sharp boundaries. The results demonstrate that our method outperforms previous approaches.