Single Image Super-Resolution Using Sparse Representation on a K-NN Dictionary

Abstract

This paper presents a new method of generating a high-resolution image from a low-resolution image. We use a sparse representation based model for low-resolution image patches. We use large patches instead of small ones of existing methods. The size of the dictionary must be large to guarantee its completeness. For each patch in the low-resolution image, we search for similar patches in the dictionary to obtain a sub-dictionary. To define the similarity and to speed up the searching process, we present a Restricted Boltzmann Machine (RBM) based binary encoding method to get binary codes for the low-resolution patches, and use Hamming distance to describe the similarity. With the KNN dictionary of each low-resolution patch, we use a sparse representation method to get its high-resolution version. Experimental results illustrate that our method outperforms other methods.

1 Introduction

Single image super-resolution (SR) refers to the task of generating a high-resolution (HR) image from a low-resolution (LR) image. It is useful in many applications, such as medical imaging, video surveillance and remote sensing imaging. Since many HR images can produce the same LR images, and SR is the reverse process, so SR is inherently ill-posed. Various SR methods have been proposed to stabilize the inversion of this ill-posed problem.

SR methods can be roughly classified into three categories: interpolation based, reconstruction based and learning based methods. Interpolation based methods (e.g., [1, 2]) are simple and fast, while they tend to smooth edges and cause blurring problems. Reconstruction based methods (e.g. [4]) apply various smoothness priors, and the enforced priors are typically designed to reduce edge artifacts. The performance of reconstruction based SR methods degrades rapidly when the number of available input images is small or the desired magnification factor is large. Learning based methods are the most popular ones. These methods either exploit internal similarities of the same image [5, 13], or reconstruct the high frequency details from a training set of LR and HR patch pairs [6, 7]. However, these methods use a unique dictionary for all the patches, and the patch size is relatively small, which may limit the SR result.

In this paper, we propose a novel SR algorithm which is based on sparse representation. Unlike existing sparse representation methods, ours employ an RBM based binary encoding method for nearest neighbor searching and uses KNN as the dictionary of each patch to conduct sparse representation.

The contributions of this paper are summarized as follows: (1) An RBM based binary encoding method is used to retrieve the KNN of each patch. (2) Using KNN as dictionary for each patch minimizes the reconstruction error in sparse representation, which leads to better SR result. (3) Large patches are employed instead of small ones as the atoms of dictionaries. Since a large patch contains more meaningful information than a small one, more high frequency details are retained in SR results.

2 Methods

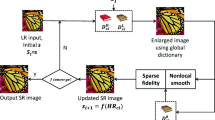
In this section, we present our sparse representation based super-resolution method. In Sect. 2.1, we will introduce dictionary preparation related work. RBM based binary encoding method is introduced in Sect. 2.2. We use this method to encode each LR patch in $D_l$ and the input LR image. We use the KNN of each LR patch retrieved by the binary codes to conduct sparse representation reconstruction, which is introduced in Sect. 2.3. The flowchart of our method is shown in Fig. 1.

Fig. 1.

The flowchart of our super-resolution algorithm.

2.1 Dictionary Preparation

Sparse representation based methods are widely used in learning-based super-resolution field [16, 17]. An over-complete dictionary pair is important for these methods. Many SR methods focus on learning an efficiency dictionary [3, 15]. To prepare the dictionary pair, we download HR images from Internet as our training set. For each HR training image, we generate the corresponding LR image by blurring and down-sampling. For LR images, we conduct bicubic interpolation to ensure that their sizes are the same as their HR images. We are interested in the patches with ample texture. For this purpose, we use Canny operator to get edges in the LR images, and extract the LR patches that center at edges. HR patches are extracted at the same position in the corresponding HR images.

We use large patches instead of small ones to combine the dictionary pair $D_l$ and $D_h$, and set the patch size as $19 \times 19$. To ensure the completeness of the dictionary with large patches, we set its size as $10^8$. Since the dictionaries are huge, (for instance, the LR dictionary $D_h$, with the feature dimension $d=19 \times 19=361$, and patch number $N=10^8$,) the total integer number is over than $10^{10}$, which needs about tens of Gigabytes. Obviously, computer memory can not load them all at once, so we divide them into 100 blocks respectively and handle them in block order.

2.2 RBM Based Binary Encoding Model

RBM based binary encoding model was proposed in [10]. Compact binary codes are learned via a stack of RBMs, each of which is trained by using the hidden activities of the previous RBM as its training data. This type of network is capable of capturing higher order correlations between different layers of the network. Each time a new RBM is added to this stack, the model has a better variational lower bound on the log probability of the data.

An RBM is a fully connected bipartite graph with one visible input (feature) layer $\mathbf v \in \mathbb {R}^{I\times 1}$ and one hidden (coding) layer $\mathbf h \in \mathbb {R}^{J\times 1}$, in which I and J represent the number of units of feature layer and coding layer respectively. Each unit has an input bias: represented as $c_i$ for the feature layer and $b_j$ for the coding layer. The layers are connected via undirected weights $\mathbf W \in \mathbb {R}^{I\times J}$. The activation probabilities of units are computed by sampling from the opposite layer with a sigmoid activation function, formulated as follows:

$$\begin{aligned} P(h_j|\mathbf v )=\text{ sigmoid }(b_j+\sum \limits _{i\in I}\omega _{ij}v_i), \end{aligned}$$

(1)

$$\begin{aligned} P(v_i|\mathbf h )=\text{ sigmoid }(c_i+\sum \limits _{j\in J}\omega _{ij}h_j), \end{aligned}$$

(2)

where $v_i$ and $h_j$ represent the state of units in the visible and hidden layers respectively.

The energy function of the RBM [10] is formulated as:

$$\begin{aligned} \nonumber E(\mathbf v ,\mathbf h )&=-\log P(\mathbf v ,\mathbf h )\\&=-\sum \limits _{i\in I}\sum \limits _{j\in J}v_i\omega _{ij}h_j-\sum \limits _{i\in I}c_iv_i-\sum \limits _{j\in J}b_jh_j \end{aligned}$$

(3)

The parameters $\mathbf W \in \mathbb {R}^{I\times J}$, $\mathbf b \in \mathbb {R}^{J\times 1}$ and $\mathbf c \in \mathbb {R}^{I\times 1}$ are updated with the objective of minimizing the energy function. The optimization method is called contrastive divergence (CD). A detailed introduction of the optimization process is given in [11]. With this optimization method, the update rules of parameters are formulated as:

$$\begin{aligned}&\varDelta w_{ij}=\epsilon (<v_ih_j>_{data}-<v_ih_j>_{recon}),\end{aligned}$$

(4)

$$\begin{aligned}&\varDelta b_j=\epsilon (<h_j>_{data}-<h_j>_{recon}),\end{aligned}$$

(5)

$$\begin{aligned}&\varDelta c_i=\epsilon (<v_i>_{data}-<v_i>_{recon}), \end{aligned}$$

(6)

where $\epsilon$ is the learning rate, $<\cdot >_{data}$ represents the sample result, and $<\cdot >_{recon}$ represents the distribution of the model.

We implement this model with four layers: an input layer, two hidden layers and an output layer. The unit numbers used in each layer are $1444-1444-722-64$. The input unit number is determined by the high-frequency feature number of an LR patch, which is with the patch size as 19 and 4 directional high-frequency features. The output unit number 64 is the length of binary codes. The unsupervised training phase is executed layer by layer from input to output. We use the trained parameters to generate binary codes for patches in $D_l$ and LR image. To reduce noise, we use the probabilities rather than the stochastic binary states in the generate process. The binary codes are the binarization results of output values of output units.

Figure 2 shows an example of similar patches retrieved in the LR dictionary $D_l$. From this figure, we get that the proposed binary encoding method preserves the local characteristics of patches.

Fig. 2.

Example of similar patches retrieved in the LR dictionary $D_l$.

2.3 Sparse Representation Based Super Resolution

In this section, we present our sparse representation based super-resolution method. Unlike existing sparse representation methods, ours uses KNN as dictionary for each LR patch. And it is realized by the RBM based binary encoding method presented in the previous section. We first conduct binary encoding to $D_l$ and the LR patch $x_i$, and search the nearest neighbors of $x_i$ in $D_l$ using the hamming distance of their binary codes. The nearest neighbors compose the sub-dictionary $D_l(i)$. Since the atoms in the dictionaries are similar to their corresponding patches, the dictionaries are efficient enough, so that we do not need any dictionary learning method.

For each LR patch $x_i$ in the original LR image, we get its LR dictionary $D_l(i)$ by KNN and the corresponding HR dictionary $D_h(i)$. The patch $x_i$ can be represented as a sparse linear combination in dictionary $D_l(i)$, and the problem of finding the sparsest representation of $x_i$ can be formulated as

$$\begin{aligned} \min ||\alpha ||_0\quad \text{ s.t. }\quad ||FD_l(i)\alpha -Fx_i||^2_2\le \epsilon , \end{aligned}$$

(7)

where F is a high-frequency (HF) feature extraction operator, which is composed of the following high-pass operators:

We concatenate the four different directional HF features as one vector as the HF feature extraction operator F.

Since the optimization problem (7) is NP-hard, we approximate the $\ell _0$ norm with the $\ell _1$ norm, which can be formulated as

$$\begin{aligned} \min ||\alpha ||_1\quad \text{ s.t. }\quad ||FD_l(i)\alpha -Fx_i||^2_2\le \epsilon \end{aligned}$$

(8)

Theoretical study results [8] prove that as long as the coefficient $\alpha$ is sufficiently sparse, the solutions of optimization problems (7) and (8) are equivalent. Lagrange multipliers offer an equivalent formulation to (8), which is formulated as

$$\begin{aligned} \alpha ^*=\mathop {{{\mathrm{argmin}}}}\limits _{\alpha }\lambda ||\alpha ||_1+\frac{1}{2}||FD_l(i)\alpha -Fx_i||^2_2, \end{aligned}$$

(9)

where the parameter $\lambda$ balances the fidelity of the approximation to $x_i$ and sparsity of the solution. We recommend to set $\lambda \in [0.1,0.3]$. In statistical literature, this problem is called LASSO [9].

Another important issue is to guarantee the compatibility of adjacent patches. We solve this problem by a one-pass algorithm similar to the method in [14]. The basic idea is that the reconstruction result $D_h(i)\alpha$ should be close to the previously computed adjacent HR patches in the overlapping areas. With this constraint, the optimization problem can be formulated as

$$\begin{aligned} \begin{array}{ll} \min ||\alpha ||_1\quad \text{ s.t. } &{}||FD_l(i)\alpha -Fx_i||^2_2\le \epsilon _1,\\ &{}||PD_h(i)\alpha -\omega ||^2_2\le \epsilon _2, \end{array} \end{aligned}$$

(10)

where the matrix P extracts the overlap region between the previously reconstructed HR result and the current patch, and $\omega$ contains the previously reconstructed HR image on the overlap. The optimization problem (10) can be rewritten as

$$\begin{aligned} \alpha ^*=\mathop {{{\mathrm{argmin}}}}\limits _{\alpha }\lambda ||\alpha ||_1+\frac{1}{2}||\hat{D}\alpha -\hat{x}||^2_2, \end{aligned}$$

(11)

where $\hat{D}=\left[ \begin{array}{l}FD_l(i)\\ PD_h(i)\end{array}\right]$ and $\hat{x}=\left[ \begin{array}{l}Fx_i\\ \omega \end{array}\right]$. After computing the optimal solution $\alpha ^*$ of (11), the HR patch can be reconstructed as $x_i^*=D_h(i)\alpha ^*$.

After patch-based reconstruction, a global reconstruction constraint is enforced to get final super-resolution result. The global constraint can be formulated as:

$$\begin{aligned} Y^*=\mathop {{{\mathrm{argmin}}}}\limits _{Y}||Y-Y_{sr}||\quad \text{ s.t. }\quad X=DBY, \end{aligned}$$

(12)

where $Y_{sr}$ is the SR result of patch-based sparse representation method, X represents the LR version of Y, B represents the blurring filter, and D represents the down-sampling operator.

Fig. 3.

Average PSNR results of ten benchmark images with different patch sizes.

Formula (12) is solved using back-projection method by an iterative strategy, which is formulated as

$$\begin{aligned} Y_{t+1}=Y_{t}+((X-DBY_{t})\uparrow s)*p, \end{aligned}$$

(13)

where $Y_t$ is the estimated high-resolution image after the t-th iteration, $\uparrow s$ represents up-sampling by the factor of s, and p is the “back-projection” filter. The details of this global reconstruction constraint is explained in [6].

3 Experiments

We apply our algorithm to benchmark images including Pepper, Lena, Foreman etc., and compare the results with those of the bicubic, NE [12], Freeman and Liu [7], Yang et al. [6], Peleg and Elad [18] and SRCNN [19] methods. We test with different magnification factors respectively, and use PSNR to measure and compare these methods.

Fig. 4.

SR results of image Lena. From top to bottom, left to right: ground truth, bicubic interpolation, NE based [12], Freeman and Liu [7], Yang et al. [6], Peleg and Elad [18], SRCNN [19] and proposed method. The magnification factors is 2.

Fig. 5.

SR results of image Foreman. From top to bottom, left to right: ground truth, bicubic interpolation, NE based [12], Freeman and Liu [7], Yang et al. [6], Peleg and Elad [18], SRCNN [19] and proposed method. The magnification factors is 4.

Fig. 6.

SR results of image Butterfly. From top to bottom, left to right: ground truth, bicubic interpolation, NE based [12], Freeman and Liu [7], Yang et al. [6], Peleg and Elad [18], SRCNN [19] and proposed method. The magnification factors is 8.

Table 1. Experimental results of PSNR index on benchmark images

3.1 Parameter Settings

There are three important parameters in this algorithm: patch size, dictionary size and sub-dictionary size (the KNN number of a patch). To investigate the impact of different patch sizes, we fix all other parameters of this algorithm and record the average PSNR indicators of ten benchmark images. Experimental results in Fig. 3 show that larger patches result in better SR results. While the calculation time increases rapidly with an increase of patch size. To balance the efficiency and performance, we choose the patch size as 19 in our experiments (Fig. 4).

Theoretically, larger dictionary size and sub-dictionary size result in better SR results, while larger dictionary means more retrieve time and storage space. Limited by the capability of our computer, we set dictionary size as $10^8$, and sub-dictionary size as 2000.

3.2 Experimental Results and Comparison

We compare our algorithm with other algorithms under different magnification factors (MF). Figure 6 shows the SR results with different magnification factors. From the first row to the third row, the magnification factors are 2, 4 and 8 respectively. Table 1 shows the PSNR results tested on several benchmark images. From this figure and table, we get that our algorithm outperforms others. And the advantage is obvious when the magnification factor is large (Fig. 5).

4 Conclusion

Experimental results demonstrate the effectiveness of our SR method, especially when the magnification factor is large. We adopt a RBM based binary encoding model for super-resolution, and use the KNN of a patch to combine its sub-dictionary. Because the KNN dictionary can minimize the reconstruction error, and the large patch size contains more information, the super-resolution result is better than the state-of-art of super-resolution methods.

Further improvement can be realized through a property hashing method, which can accelerate the KNN searching process. On the other hand, a fast dictionary learning method may be added to make the dictionary more compact, which may further improve the super-resolution result.