Symmetric Masks for In-fill Pixel Interpolation on Discrete p:q Lattices

Abstract

A 2D p:q lattice contains image intensity entries at pixels located at regular, staggered intervals that are spaced p rows and q columns apart. Zero values appear at all other intermediate grid locations. We consider here the construction, for any given p:q, of convolution masks to smoothly and uniformly interpolate values across all of the intermediate grid positions. The conventional pixel-filling approach is to allocate intensities proportional to the fractional area that each grid pixel occupies inside the boundaries formed by the p:q lines. However these area-based masks have asymmetric boundaries, flat interior values and may be odd or even in size. We ask here if smoother, symmetric versions of such convolution masks exist and, if so, is their structure unique for each p:q lattice? The answer appears to be yes on both counts. The coefficients of the masks constructed here have simple integer values whose distribution is derived purely from symmetry considerations. We have application for these symmetric interpolation masks as part of a precise image rotation algorithm, as well as to smooth back-projected values when performing discrete tomographic image reconstruction.

1 Introduction

We consider here the problem of distributing regularly-spaced but sparse image intensities to fill the gaps between known values. The known values are located at discrete pixel locations that fall on straight lines oriented at an angle $\theta$, whose tangents are rational fractions, for example $\theta = tan(q/p)$, where p and q are co-prime integers. When p or q is negative, $\theta$ becomes $-\theta$.

The values at all other grid locations are set to zero. We call this 2D set of sparse image points a p:q lattice. These lattices occur as a result of affine rotation of discrete images [1, 7] and also when discrete 1D projected views of a 2D image are back-projected across a 2D space when reconstructing images from projections [4].

The way we choose to perform pixel in-filling on a p:q lattice is important. Interpolation changes the spectral content of the original image through the process of convolving the distribution of interpolating mask values with the original image values that are now spread across a p:q lattice.

Masks for pixel in-filling are traditionally defined on the basis of area intersection: the value interpolated at each vacant pixel position depends on the fraction of each pixel area that lies inside the bounding lines of the p:q lattice [7].

This paper presents a method to construct symmetric in-fill masks. These masks provide an alternative to conventional asymmetric, area-based masks. We compare the effects of mask symmetry on in-filled images when they are subsequently down-scaled as part of an image rotation scheme. We also examine the use of symmetric masks to smooth discrete projection data.

An affine rotation of discrete image data, at an angle $\theta$, remaps the content of the original image pixels located at (x, y) to a new image with pixels positioned at where (using Matlab notation), = [q −p 0; p q 0; 0 0 1]*[x; y; 1] in homogeneous image coordinates. This rotation also expands a square of unit area to have area $A = p^2+q^2$, leaving all the intermediate pixel values as zero. Pixel in-filling ‘joins the dots’ between known values in the up-scaled and rotated data, producing a smooth grey-scale image.

Fig. 1.

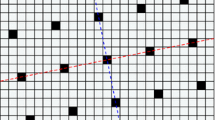
Left: a 1:5 lattice image. Right: the same image after interpolation using the area-based mask shown in Fig. 2

Discrete projection of an image involves summing pixel values along parallel rays to form a 1D sum of the 2D image data at orientation p:q. Collecting views at a set of different p:q angles permits reconstruction of the 2D image from its 1D projections (discrete tomography, [4]). One method by which images can be reconstructed is through back-projection of the 1D data across the 2D image plane, usually with a filtration step to reduce the anomalies that occur when mapping polar samples back across a Cartesian grid. The process of back-projecting 1D data generates p:q lattices at each view angle, for which these interpolation masks again prove useful.

Where many neighbouring p:q lattice values have the same intensity, these interpolating masks must all produce an exactly uniform response for all pixels that lie between those lattice points. An example of a 1:5 lattice image is shown in Fig. 1, together with the image the results after convolving with the area-based mask shown in Fig. 2.

The area-based interpolation masks (Fig. 2) have asymmetric edges (along which the area fractions change quite rapidly) with very flat interiors since the areas of most ’internal’ pixels are fully included. These masks can be odd or even in size and hence have an ambiguously-positioned centre for interpolation. The values in the mask for a p:q lattice need to be transposed for use on a q:p lattice. The transpose of the masks shown in Fig. 2 must be used to in-fill pixels on a 5:1 and 5:3 lattice, respectively. 1D projection of these 2D area-based masks is equivalent to forming the corresponding Haar interpolation filter [4].

Fig. 2.

Area-based interpolation mask coefficients. Left for a 1:5 lattice, right for a 3:5 lattice

This paper is organised as follows: Sect. 2 outlines a method to construct symmetric pixel in-filling masks for any p:q. Section 3 presents examples of in-filled lattice structures, and discusses the uniqueness properties of these masks and compares results obtained using symmetric and area-based masks. Section 4 presents image rotation examples obtained using symmetric and the conventional masks. Section 5 examines filters built as 1D projection of the 2D area-based and symmetric masks, whilst Sect. 6 looks at future extensions of this work.

2 Construction of Symmetric Interpolation Masks

To construct a symmetric mask for any p:q lattice, we require just that the mask coefficients have fourfold symmetry (assuming we use a square grid) and that the four nearest neighbours on a p:q lattice (call them A, B, C and D) contribute equally to form the value of the single pixel (or group of pixels) that lie at the geometric centre of these 4 lattice points.

To contribute equal proportions to the intensity at the centre pixel(s) we expect A, B, C and D to add as [1, 1, 1, 1], i.e. each adds 25 % of their value to the final central value. Off-centre pixels are then expected to add as [2, 1, 1, 0], [2, 2, 0, 0], [3 1, 0, 0] and finally [4, 0, 0, 0] for pixels that lie at or close to lattice points A, B, C or D. The symmetric mask coefficients thus only contain integer values of 0, 1, 2, 3, or 4, since we combine intensities in multiples of 25 % portions.

When $s = p+q+1$ is odd, there is a single pixel for which A, B, C and D combine equally as [1, 1, 1, 1] and the mask has size s*s. When s is even, there will be 4 central pixels located exactly between A, B, C and D, each of which will be summed as [1, 1, 1, 1]. The mask size is then $(s+1)*(s+1)$. Note that the full mask size, S, is now always odd. Let the mask have coefficients M(x, y), where $-w \le x$, y $\le +w$, and where $w = (S-1)/2$. All coefficients of M that fall outside the S*S area are assumed to have value zero.

Fig. 3.

Construction of 1:5 symmetric mask values from 4 points (labelled A (red), B (green), C (grey) and D (blue) on a 1:5 lattice. Point D is located 1:5 steps from point A. Point B is located 5:1 steps from point A. The 4 numbers clustered around each location denote the relative contribution summed to that point by each of the 4 lattice pixels. The four numbers, starting anticlockwise from bottom left, come from lattice points A, B, C and D, respectively. The same symmetric 7*7 mask M(x, y) is placed with its centre at each of the 4 lattice points. The fourfold symmetry means we only need to find one octant of the coefficients in M. The yellow square marks the initial centre pixel (it is equidistant to A, B C and D). It is initialised with equal contributions [1, 1, 1, 1] from A, B, C and D as the starting point and from which we find all of the remaining coefficients of the mask M. Where two options to fill a pixel are possible (shown in smaller font), we choose the maximum of those two values (the resulting values that get selected are shown here as bold) (Color figure online)

2.1 Rules for Constructing Symmetric Masks to In-fill p:q Lattice Pixels

• (1) The coefficients for contributions from points A, B, C and D are set to [1, 1, 1, 1] at the position of the single centre pixel when s is odd. The same values are applied at the four centremost pixels when s is even.

• (2) If $M(x, y) = v$, then $M(x, -y) = M(-x, \pm y) = M(\pm y, \pm x)$ = v, i.e. four-fold symmetry, {v = 0, 1, 2, 3 or 4}

• (3) Lattice point $D = 4-v$ when A, B, C = [0, 0, v], [0, v, 0] or [v, 0, 0].

• (4) If $M(x \pm 1, y) = v$ or $M(x, y \pm 1) = v$, then $M(x, y) \ge v$, monotonicity

• (5) If $M(x, y) = u\Vert v$, then $M(x, y) = max(u, v)$ when a paired choice possibility arises

Figure 3 provides an example of the construction method used to find the coefficients for the 7*7 symmetric interpolation mask M for $p{:}q = 1{:}5$. Figure 4 summarises the final coefficients of M as obtained from Fig. 3.

It seems that simply imposing four-fold symmetry and requiring equal sharing at the centre pixel location(s) is sufficient to constrain the values for all of the coefficients of M(x, y) for any p:q. It is however tedious to work manually thorough the symmetry points to establish values for each of the coefficients for large p:q. It would be gratifying to have a theoretical proof that the conditions imposed above are necessary and sufficient for all p:q.

Fig. 4.

Symmetric coefficients M for a 1:5 lattice. Left: using the maximum value (Rule 5) when forced to choose. Right: resulting mask from the alternate choice

Fig. 5.

Symmetric coefficients for 1:7 (9*9 mask) and 3:7 (11*11 mask) lattices

Figure 5 shows example mask coefficients of M for the lattice directions 1:7 and 3:7. A symmetric mask can be found for each p:q that we have tried. To date, we have no counter examples.

3 Mask Performance for Pixel In-filling

For a p:q lattice that has constant intensity values, the interpolated response must be exactly flat for all interior pixels of a finite lattice of any size. Figure 6 shows in-filled lattices for $p{:}q = 1{:}5$ and 3:7 for a small triangular area containing 15 lattice pixels. The matching result for the same traditional area-based filter is shown for comparison. As expected, by construction, the interior region for all masks is exactly flat.

The borders of the in-filled regions provide an indication of how the masks perform when there are different values at the nearest lattice points. In-filled pixels in the interior of these binary shapes will be interpolated from four know values and will (by design) result in perfectly smooth values. Pixels near the edge of the binary shape will have in-filled values interpolated from one, two or three known values. Thus the edge pixel intensities depend strongly on the design of the mask coefficients.

The size of the symmetric interpolating masks is always larger than the area masks (because these masks extend across the centre pixel region) so the symmetric interpolated edges are wider, but the interpolated edge values are better aligned with the row and column axes.

Fig. 6.

A triangular area of uniform valued lattice pixels filled by, left to right: $p{:}q = 1{:}5$ area filled then symmetric filled, $p{:}q = 3{:}7$, area filled then symmetric filled

Fig. 7.

Interpolated images for 3:5 lattice points inside a triangular area containing 15 points using (left to right) the four mask values shown in Fig. 8(a) to (d) respectively. The original unit-intensity lattice pixel positions are shown as the black points inside the triangular area

If the rules for symmetric filling are relaxed (in particular Rule 5), then alternate versions of these filters can be constructed, as was also shown in Fig. 4. Figure 7 shows the resultant in-filling for a small triangle of points on a 3:5 lattice. The position of each original lattice pixels is shown here as a black point inside the triangle. Results for three different symmetric masks as well as the area-based mask are shown. The mask values are given in Fig. 8. Mask (d) of Fig. 8 adheres to the full rules for symmetric mask generation as it has the broadest spread, which is ensured by requiring that the maximum coefficients occur along the periphery of the mask.

Fig. 8.

Alternate forms for 3:5 lattice masks. (a) Traditional area-based, (b) to (d) using variations of Rule 5 to select between tied values for coefficients of symmetric masks M(x, y). (b) Minimum, (c) intermediate, (d) maximum

4 Rotation of Images by p:q and q:p

4.1 Discrete Rotation Angles

Whilst it is common to use simple units of degrees for angular measurements, it turns out that discrete angles defined by p:q ratios provide good coverage of uniformly-spaced angles when using reasonably small values of p and q (naturally any angle can be approximated with arbitrary precision by atan(q / p) using arbitrarily large integers p and q). For example, of the 44 angles from $1^{\circ }$ to $44^{\circ }$ in $1^{\circ }$ steps, 27 of these angles can be approximated to within $\pm 0.5^{\circ }$ as discrete p:q ratios with |p| and $|q| \le 11$.

Another nice feature of discrete rational angles is the way they can be combined to reach multiples of 90$^{\circ }$. For example, a rotation of $p{:}q = \theta$ followed by $q:p = 90^{\circ } - \theta$ is a $90^{\circ }$ rotation for any choice of p:q. Similarly, we can find sets of distinct p:q rotations that cumulatively effect a net rotation by a multiple of $90^{\circ }$. For example, the net rotations {7:4, 7:6, 1:5, 1:7, 3:4, 1:4} is exactly $180^{\circ }$.

4.2 Measuring the Quality of Rotated Images

Rigorous, perceptually-based measures of image quality to assess digital image rotation algorithms are difficult to design and use. The fidelity of a rotated image depends on the rotation angle as well as the image content. There is no way to evaluate a rotated image without recourse to a ‘golden standard’.

We then resort to using rough but simple physical measures such as mean squared error (MSE) and peak signal to noise ratio (PSNR). The choice of angle at which to compare the efficacy of different rotation algorithms is again somewhat arbitrary. Many algorithm evaluations have used multiple rotations by the same angle to arrive at a cumulative rotation such as $90^{\circ }$ or $180^{\circ }$, for which we can make an exact comparison copy for any image data (for example, $6*15^{\circ }$ rotations = $90^{\circ }$). This strategy is better than using rotations of $+\theta$ followed by $-\theta$ to effect a net zero degree rotation, because the positive and negative rotation errors of a given algorithm can contrive to cancel exactly, giving the illusion that each $\theta$ rotation was perfect. However the interpretation that can be assigned to the quality of a single rotation of $16^{\circ }$ is unclear, when given an MSE obtained for 6 successive such rotations (the interpolation effects of rotations are not linearly cumulative, especially when the same angle is used repeatedly).

Here we choose to use sets of 6 different p:q rotations and then apply the 6 rotations many times in randomised order to get a mean quality measure. We can then apply the same test using 5 or 7 sets of similar angles to judge the level of distortion contributed by adding or subtracting one extra rotation.

4.3 Rotation Algorithms

Algorithms for efficient discrete image rotation date from the beginnings of computer vision (for example [3]). The three-pass skew algorithm [2, 5, 6] that was developed more recently seems to perform exceptionally well. Another means to accurately rotate images is by extending (by reflection) the sinogram of a high precision conventional $180^{\circ }$ Radon transform to cover projection angles $0^{\circ }$ to $360^{\circ }$ and then indexing the ‘zero’ starting angle to the required rotation angle for precise image reconstruction (by filtered back-projection, for example).

Here we perform an exact, lossless p:q affine image rotation, then apply the p:q in-fill masks M(x, y) to interpolate the image that is now up-scaled in area by $p^2+q^2$. The (potentially large) increase in the up-scaled image size is not a problem if the computer memory capacity permits. We then downsize the rotated image by factor $f=1/\sqrt{p^2+q^2}$ along both column and row axes to obtain a rotated image at the original image scale. The quality of the final rotated image then depends on only the pixel in-fill method applied and the method used for image downsizing (although we apply Gaussian smoothing to the up-scaled and in-filled image before downsizing to reduce the aliasing).

Surprisingly, the supposedly simple process of downsizing images causes a lot of variation in the rotated image. We tried to stabilize these results by pre-rotating a test image. The test image, of the same size as the original data, is comprised of a unit-valued pixel located at the rotation centre, with between 7 to 10 unit-valued pixels, placed at nearly equal-spaced angular intervals, around the perimeter of a circle drawn about the image centre.

Fig. 9.

Six successive rotations, by {1:7, 1:5, 3:4, 7:4, 7:6, 1:4}, of a test image (a 509 $\times$ 509 portion of boats.jpg) for which the final accumulated angle is $180^{\circ }$. Top row: symmetric masks, middle row: area-base masks, bottom row: normalised difference images. The resulting net PSNR (measured over a circular region with a diameter just inside the final aperture), remains about $33\pm 3$ for the same set of angles for the same set of rotations performed in random order

The test image is then up-scaled by the selected p:q rotation and convolved with the appropriate p:q in-fill mask. We then shift and zero-pad this test image until the downsizing by the scale factor f preserves the intensity of the rotated test image centre pixel and perimeter pixels to better than 95 % (where possible). We then downsize the rotated up-scaled and in-filled original image data, applying the optimal shift and pad values that best preserved the test image pixels.

Figure 9 shows a typical result obtained for the set of rotations {7:4, 7:6, 1:5, 1:7, 3:4, 1:4}. The PSNR of the final result has a mean value of around $33\pm 3$, depending on the order in which the rotations are performed. This result is consistent with the values we obtained using traditional bi-linear or bi-cubic interpolation algorithms, but poorer than for the three-pass skew rotation method [2, 5, 6], which averaged a PSNR closer to 40.

The symmetric masks can perform better than the area-based masks because of the enforced alignment of the interpolated values along the image rows and columns, providing that the downsizing step can be well synchronised.

We observed ‘perfect’ results (precisely zero MSE) using the symmetric masks for a net $90^{\circ }$ rotation done as 3:4 followed by 4:3 (provided no anti-alias smoothing is applied). The downsizing factor for 3:4 is an exact integer, $f = \sqrt{3^{2}+4^{2}} = 5$. The intermediate image is however not perfect. It is clear that here the visible 3:4 rotation errors are exactly undone by the 4:3 rotation.

5 Projections of 2D Symmetric Masks for 1D Haar Interpolation

The in-filling of pixels on a p:q lattice also has relevance for back-projecting data on a grid at discrete angles. The summation of discrete pixels along a line (under the Dirac model) can be converted to area-based integrals (that represent rays of finite width) by convolving the 1D Dirac projections with Haar filters. The appropriate Haar filter for projection p:q is the 1D projection of the 2D area-based p:q mask [4].

Figure 10 displays the 1D projection at 3:5 for the 3:5 area-based and symmetric masks. The projection profiles are notably distinct and reflect the very different underlying assumptions behind their construction. Haar filtered back-projected images for direction 3:5 that arise from a point are also shown for comparison. Because the symmetric filters all have odd size, the 2D filled back-projection can always be replicated exactly by 1D convolution of the projected data for any p:q. For area-based masks where $p+q$ is even, the 1D back-projection is misaligned at the edges of the in-filled rays.

Fig. 10.

Top row, left to right: normalised 3:5 projection of the 2D 3:5 mask for area-filled and symmetric masks, then area-based and symmetric in-filled back-projection of a single image point at angle 3:5. Black points mark the position of the original un-filtered back-projected pixels. Bottom row: normalised 1D column (or row) sums of the 2D 3:5 masks, left, area-based mask, right symmetric mask.

6 Conclusions and Future Work

We considered here the construction of convolution masks to uniformly in-fill pixels on p:q lattices using simple symmetry constraints, rather than the traditional area-based assumptions. We tested the efficiency of these interpolation masks when used as part of a discrete rotation algorithm. The quality of the image rotations obtained using the symmetric masks was at least as good and usually better than that when using the area-based versions.

We have yet to examine how these symmetric masks perform in discrete image reconstruction when used as 1D filters to smooth discrete back-projected data. The construction of 2D symmetric masks should also be able to be extended to higher dimensions, for example to M(x, y, z), using, as far as possible, the same symmetry rules as listed here in Sect. 2. It would be interesting to examine the rules that constrain the construction of six-fold symmetric 2D masks for hexagonal p:q lattices.