Computation of the Normal Vector to a Digital Plane by Sampling Significant Points

Abstract

Digital planes are sets of integer points located between two parallel planes. We present a new algorithm that computes the normal vector of a digital plane given only a predicate “is a point x in the digital plane or not”. In opposition with the algorithm presented in [7], the algorithm is fully local and does not explore the plane. Furthermore its worst-case complexity bound is $O(\omega )$, where $\omega$ is the arithmetic thickness of the digital plane. Its only restriction is that the algorithm must start just below a Bezout point of the plane in order to return the exact normal vector. In practice, our algorithm performs much better than the theoretical bound, with an average behavior close to $O(\log \omega )$. We show further how this algorithm can be used to analyze the geometry of arbitrary digital surfaces, by computing normals and identifying convex, concave or saddle parts of the surface.

This work has been partly funded by DigitalSnow ANR-11-BS02-009 research grant.

1 Introduction

The study of the linear geometry of digital sets has raised a considerable amount of work in the digital geometry community. In 2D, digital straightness has been extremely fruitful. Indeed, properties of digital straight lines have impacted the practical analysis of 2D shapes, especially through the notion of maximal segments [3, 4], which are unextensible pieces of digital straight lines along digital contours.

In 3D, the main problem is that there is no more an implication between “being a maximal plane” and “being a tangent plane” as it is in 2D. This was highlighted in [2], where maximal planes were then defined as planar extension of maximal disks. To sum up, the problem is not so much to recognize a piece of plane, but more to group together the pertinent points onto the digital shape.

A first algorithm was proposed by the authors in [7]. Given only a predicate “is point $\varvec{x}$ in plane $\mathbf {P}$ ?” and a starting point in $\mathbf {P}$, this algorithm extracts the exact characteristics of $\mathbf {P}$. The idea is to deform an initial unit tetrahedron based at the starting point with only unimodular transformations. Each transformation is decided by looking only at a few points around the tetrahedron. This step is mostly local but may induce sometimes a dichotomic exploration. At the end of this iterative process, one face of the tetrahedron is parallel to $\mathbf {P}$, and thus determines its normal. The remarkable idea is that the algorithm decides itself on-the-fly which points have to be considered for computing the local plane geometry, in opposition to usual plane recognition algorithms [1, 5, 6, 8]. This approach was thus also interesting for analysing 3D shape boundaries.

This paper proposes another algorithm that extracts the characteristics of plane $\mathbf {P}$ given only this predicate and a starting configuration. This new algorithm is also an iterative process that deforms an initial tetrahedron and stops when one face is parallel to $\mathbf {P}$. However, this new algorithm both complements and enhances the former approach. It complements it since it extracts triangular facets onto the plane whose Bezout point is above the facet, while the former algorithm extracts the ones whose Bezout point is not above the facet. See Fig. 2 for an example of execution of both algorithms with the same input. It is also a geometrical algorithm using convex hull and Delaunay circumsphere property, while the former was mostly arithmetic. It enhances it for several reasons. First, its theoretical complexity is slightly better (it drops a $\log$ factor) and it is faster also in practice. Second, we control the position of the evolving tetrahedron, which always stays around the starting point. Third, each step is purely local and tests the predicate on only six points. Fourth, it can detect planarity defects onto digital surfaces that are not digital planes. Last, a variant of the proposed algorithm almost always produce directly a reduced basis of the lattice of upper leaning points, without lattice reduction. Of course, this algorithm presents one disadvantage with respect to the former one: the starting configuration must lie at a reentrant corner of the plane, more precisely below the Bezout point of the plane. If it starts at another corner, then the algorithm will stop sooner and outputs only an approximation of the normal of $\mathbf {P}$.

The paper is organized as follows. First, we give basic definitions and present our new algorithm. Second we show its correctness and exhibit worst-case upperbound for its time complexity. Third we study how often this algorithm extracts a reduced basis of the lattice of upper leaning points and present a variant — with the same properties — that returns almost always a reduced basis. Afterwards we exploit this algorithm to determine the linear geometry of digital surfaces, and we show how to deal with starting configurations that are not under the Bezout point. Finally the pros and cons of this algorithm are discussed and several research directions are outlined.

2 Notations and Algorithm

In this section, we introduce a few notations before presenting our new algorithm. A digital plane is defined as the set

$$\begin{aligned} \mathbf {P}= \{ \varvec{x}\in \mathbb {Z}^3 | \mu \le {\varvec{x}\cdot \mathbf {N}} < \mu + {\mathbf {s}\cdot \mathbf {N}}\}, \end{aligned}$$

where $\mathbf {N}\in {\mathbb {Z}}^3$ is the normal vector whose components (a, b, c) are relatively prime, $\mu \in {\mathbb {Z}}$ is the intercept, $\mathbf {s}$ is the shift vector, equal to $(\pm 1,\pm 1,\pm 1)$ in the standard case.

By translation, we assume w.l.o.g. that $\mu = 0$. Moreover, by symmetry, we assume w.l.o.g. that the normal of the plane lies in the first octant, i.e. its components are positive. We also exclude cases where a component is null since then it falls back to a 2D algorithm. Thus, $a,b,c >0$ and $\mathbf {s}= (1,1,1)$. Finally, we denote by $\omega := {\mathbf {s}\cdot \mathbf {N}}=a+b+c$ the thickness of the standard digital plane $\mathbf {P}$.

The above definition of digital plane suggest to see the space as partitionned into layers of coplanar points, orthogonal to $\mathbf {N}$. The value ${\varvec{x}\cdot \mathbf {N}}$, called height, is a way of sorting these layers in direction $\mathbf {N}$. Points of height 0 (resp. $\omega - 1$), which are extreme in $\mathbf {P}$, are called lower leaning points (resp. upper leaning points). Points of height $\omega$, the closest ones above $\mathbf {P}$, are called Bezout points.

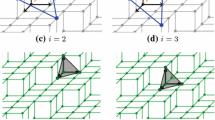
Algorithm 1 finds $\mathbf {N}$ given a predicate “is $\varvec{x}\in \mathbf {P}$ ?”. The algorithm starts at any reentrant corner as follows: the corner point $\varvec{p}$ is in $\mathbf {P}$; the shifted point $\varvec{q}:= \varvec{p}+\varvec{s}$ is not in $\mathbf {P}$ since ${\varvec{s}\cdot \mathbf {N}}$ is the thickness of $\mathbf {P}$; the initial triangle ${\mathbf {T}}^{(0)} := ( \varvec{v}_{k}^{(0)} )_{k {~\in \{0,1,2\}}}$ is such that $\forall k, \varvec{v}_{k}^{(0)} := \varvec{p}+\varvec{e}_{k}+\varvec{e}_{k+1}$ (Fig. 1.c). It is easy to check that ${\mathbf {T}}^{(0)} \subset \mathbf {P}$ for any $\varvec{p}$ such that $0 \le {\varvec{p}\cdot \mathbf {N}} < \min \{a,b,c\}$, which corresponds exactly to reentrant corners onto a standard digital plane. The algorithm then updates this initial triangle and iteratively aligns it with the plane by calling the above predicate for well-chosen points, until the solution equals $\mathbf {N}$.

At step $i \in {\mathbb {N}}$, the solution is described by a triangle denoted by ${\mathbf {T}}^{(i)}$. Algorithm 1 is designed so that $\forall i, {\mathbf {T}}^{(i)}$ is included in $\mathbf {P}$ and is intersected by segment $[\varvec{p}\varvec{q}]$. Segment $[\varvec{p}\varvec{q}]$ thus forces the exploration to be local.

Let k be an integer taken modulo 3, i.e. $k {~\in {\mathbb {Z}}/3{\mathbb {Z}}}$. The three counterclockwise oriented vertices of ${\mathbf {T}}^{(i)}$ are denoted by $\varvec{v}_{k}^{(i)}$ (Fig. 1.a). For sake of clarity, we will write $\forall k$ instead of $\forall k {~\in {\mathbb {Z}}/3{\mathbb {Z}}}$. We also introduce the following vectors (Fig. 1.a):

$$\begin{aligned} \forall k, \ \varvec{m}_{k}^{(i)}&:= \varvec{q}- \varvec{v}_{k}^{(i)} \end{aligned}$$

(1)

$$\begin{aligned} \forall k, \ \varvec{d}_{k}^{(i)}&:= \varvec{v}_{k+1}^{(i)} - \varvec{v}_{k}^{(i)} = \varvec{m}_{k}^{(i)} - \varvec{m}_{k+1}^{(i)}. \end{aligned}$$

(2)

The normal of ${\mathbf {T}}^{(i)}$, denoted by $\mathbf {\hat{N}}({\mathbf {T}}^{(i)})$, is merely defined by the cross product between two consecutive edge vectors of ${\mathbf {T}}^{(i)}$, i.e. $\mathbf {\hat{N}}({\mathbf {T}}^{(i)}) = \varvec{d}_{0}^{(i)} \times \varvec{d}_{1}^{(i)}$.

Fig. 1.

Main notations are illustrated in (a) and (b) (iteration number as exponent (i) is dropped for sake of clarity). The starting triangle is illustrated in (c).

In order to improve the guess at step i, the algorithm checks if the points of a small neighborhood around $\varvec{q}$, parallel and above ${\mathbf {T}}^{(i)}$, belong to $\mathbf {P}$ or not. This neighborhood is defined as follows (Fig. 1.b):

$$\begin{aligned} \varSigma _{{\mathbf {T}}^{(i)}} := \left\{ \varvec{q}\pm \varvec{d}_{k}^{(i)} \right\} _{k {~\in \{0,1,2\}}}. \end{aligned}$$

(3)

The algorithm then computes $\varSigma _{{\mathbf {T}}^{(i)}} \cap \mathbf {P}$ by making six calls to the predicate. In Algorithm 1, the new triangle ${\mathbf {T}}^{(i+1)}$ is simply defined as the other triangular facet of the convex hull of ${\mathbf {T}}^{(i)} \cup (\varSigma _{{\mathbf {T}}^{(i)}} \cap \mathbf {P})$ which intersects $[\varvec{p}\varvec{q}]$. See Fig. 2 for an example. The algorithm stops when $\varSigma _{{\mathbf {T}}^{(n)}} \cap \mathbf {P}$ is empty. We show in Theorem 2 that, when $\varvec{p}$ is a lower leaning point (its height is 0), the vertices of the last triangle ${\mathbf {T}}^{(n)}$ are upper leaning points of $\mathbf {P}$ (their height is $\omega -1$). Corollary 1 implies that the normal to ${\mathbf {T}}^{(n)}$ is the normal to $\mathbf {P}$ and Corollary 2 implies that triangle edges form a basis of the lattice of upper leaning points to $\mathbf {P}$.

Fig. 2.

Illustration of the running of Algorithm 1 and algorithm from [7] on a digital plane of normal vector (1, 2, 5). Images (a) to (d) shows the four iterations of Algorithm 1 starting from the origin. For $i \in \{0,1,2,3\}$, triangles ${\mathbf {T}}^{(i)}$ are in blue, whereas neighborhood points are depicted with red disks (resp. circles) if they belong (resp. do not belong) to $\mathbf {P}$. In (d), the normal of the last triangle is (1, 2, 5). Images (e) to (h) shows iterations 0 (initial), 2, 5 and 7 (final) of the algorithm from [7]. The initial tetrahedron (a) is placed at the origin and the final one (h) has an upper triangle with normal vector (1, 2, 5) (Color figure online).

3 Validity and Complexity

In this section, we first prove the two invariants of Algorithm 1 and fully characterize its main operation (lines 3–5 of Algorithm 1). Then we prove that if $\varvec{p}$ is a lower leaning point, Algorithm 1 retrieves the true normal $\mathbf {N}$ in less than $\omega -3$ steps.

Let us assume that the algorithm always terminate in a finite number of steps whatever the starting point and let n be the last step (the proof is postponed, see Theorem 1).

3.1 Algorithm Invariants

The following two invariants are easy to prove by induction since by construction, each new triangle is chosen as a triangular facet of the convex hull of some subset of $\mathbf {P}$, which is intersected by $]\varvec{p}\varvec{q}]$.

Invariant 1

${\forall i \in \{0,\dots ,n\}}, \ \forall k, \ \varvec{v}_{k}^{(i)} \in \mathbf {P}$.

Invariant 2

${\forall i \in \{0,\dots ,n\}}$, the interior of ${\mathbf {T}}^{(i)}$ is intersected by $]\varvec{p}\varvec{q}]$.

The only difficulty in Invariant 2 is to show that the triangle boundary is never intersected by $]\varvec{p}\varvec{q}]$. Below, for lack of space, we only show by contradiction that $]\varvec{p}\varvec{q}]$ does not intersect any edge of ${\mathbf {T}}^{(i+1)}$, if Invariant 2 is assumed to be true for ${i \in \{0,\dots ,n-1\}}$.

Proof

If $]\varvec{p}\varvec{q}]$ and some edge $[\varvec{x}\varvec{y}]$ of ${\mathbf {T}}^{(i+1)}$ intersect, points $\varvec{p}, \varvec{q}, \varvec{x}$ and $\varvec{y}$ are coplanar. But, since the boundary of ${\mathbf {T}}^{(i)}$ is not intersected by $]\varvec{p}\varvec{q}]$ and since points of $\varSigma _{{\mathbf {T}}^{(i)}}$ are located on lines that are parallel to the sides of ${\mathbf {T}}^{(i)}$, $\varvec{x}$ and $\varvec{y}$ must be opposite points in $\varSigma _{{\mathbf {T}}^{(i)}}$, i.e. $\varvec{x}:= \varvec{q}+ \varvec{d}_{l}^{(i)}$ for some $l {~\in \{0,1,2\}}$ and $\varvec{y}= \varvec{q}- \varvec{d}_{l}^{(i)}$.

However, since $\varvec{q}\notin \mathbf {P}$, $\varvec{x}$ and $\varvec{y}$ cannot be both in $\mathbf {P}$ by linearity and thus cannot be the ends of an edge of ${\mathbf {T}}^{(i+1)}$, which is included in $\mathbf {P}$ by Invariant 1.    $\square$

3.2 Operation Characterization

The two following lemmas characterize the operation that transforms a triangle into the next one (lines 3–5 of Algorithm 1).

Lemma 1

${\forall i \in \{0,\dots ,n-1\}}$, ${\mathbf {T}}^{(i)}$ and ${\mathbf {T}}^{(i+1)}$ share exactly one or two vertices.

Proof

Let $\gamma$ be the number of common vertices between ${\mathbf {T}}^{(i)}$ and ${\mathbf {T}}^{(i+1)}$. Since ${\mathbf {T}}^{(i)}$ and ${\mathbf {T}}^{(i+1)}$ have three vertices each, $0 \le \gamma \le 3$, but we prove below that (i) $\gamma \ne 3$ and (ii) $\gamma \ne 0$.

Inequality (i) is trivial. Indeed, since the volume of the convex hull of ${\mathbf {T}}^{(i)} \cup (\varSigma _{{\mathbf {T}}^{(i)}} \cap \mathbf {P})$ is not empty for ${i \in \{0,\dots ,n-1\}}$ (see Algorithm 1, l. 2), we necessarily have ${\mathbf {T}}^{(i)} \ne {\mathbf {T}}^{(i+1)}$, which implies that $\gamma \ne 3$.

In order to prove inequality (ii), let $\mathcal {P}$ be the plane passing by the points of $\varSigma _{{\mathbf {T}}^{(i)}}$ (points of $\varSigma _{{\mathbf {T}}^{(i)}}$ are coplanar by (2) and (3)). Note that $\varvec{q}\in \mathcal {P}$ by (3).

Let us assume that ${\mathbf {T}}^{(i+1)}$ is included in $\mathcal {P}$. By invariant 1, ${\mathbf {T}}^{(i+1)} \subset \mathbf {P}$. However, $\varvec{q}\notin \mathbf {P}$ by definition of $\varvec{q}$. As a consequence, the upper leaning plane of $\mathbf {P}$, i.e. $\{\varvec{x}\in {\mathbb {R}}^3 | {\varvec{x}\cdot \mathbf {N}} = \omega -1 \}$, strictly separates ${\mathbf {T}}^{(i+1)}$ from $\varvec{q}$ in the plane $\mathcal {P}$. In addition, $\varvec{p}$ is located strictly below ${\mathbf {T}}^{(i)}$ by Invariant 2 and is thus also below $\mathcal {P}$, which is parallel and above ${\mathbf {T}}^{(i)}$ by definition. As a consequence, ${\mathbf {T}}^{(i+1)}$ is clearly not intersected by $]\varvec{p}\varvec{q}]$, which contradicts Invariant 2. We conclude that ${\mathbf {T}}^{(i+1)}$ is not included in $\mathcal {P}$, which means that $\gamma \ne 0$.    $\square$

The following lemma fully characterizes the main operation of Algorithm 1:

Lemma 2

${\forall i \in \{0,\dots ,n-1\}}, \ \forall k, \ \left\{ \begin{array}{l} {either }\ \varvec{v}_{k}^{(i+1)} = \varvec{v}_{k}^{(i)}, \\ {or }\ \varvec{v}_{k}^{(i+1)} = \varvec{v}_{k}^{(i)} + \varvec{m}_{l}^{(i)}, l \ne k. \end{array} \right.$

We know by Lemma 1 that ${\mathbf {T}}^{(i)}$ and ${\mathbf {T}}^{(i+1)}$ share one or two vertices. The proof is thus in two parts. In each part however, we use infinite cones of apex $\varvec{q}$ to check whether Invariant 2 is true or not. Let us define ${\forall i \in \{0,\dots ,n\}}, \ {\mathcal {T_\infty }}^{(i)}$ as the set of infinite rays emanating from $\varvec{q}$ and intersecting the triangular facet ${\mathbf {T}}^{(i)}$. Invariant 2 is equivalent to the following

Invariant 2’: ${\forall i \in \{0,\dots ,n\}}$, the interior of ${\mathcal {T_\infty }}^{(i)}$ contains $\varvec{p}$.

Fig. 3.

Illustration of the proof of Lemma 2. Case where ${\mathbf {T}}^{(i)}$ and ${\mathbf {T}}^{(i+1)}$ share $\varvec{v}_{1}^{(i)}$ and $\varvec{v}_{2}^{(i)}$ in (a), but only $\varvec{v}_{2}^{(i)}$ in (b) (exponent (i) is omitted in the figures).

Proof

We first assume that ${\mathbf {T}}^{(i)}$ and ${\mathbf {T}}^{(i+1)}$ share two vertices. Let us assume w.l.o.g. that the index of the vertex of ${\mathbf {T}}^{(i)}$ that is not in ${\mathbf {T}}^{(i+1)}$ is 0.

Since $\varvec{v}_{0}^{(i+1)} \in \varSigma _{{\mathbf {T}}^{(i)}} \cap \mathbf {P}$, there are six cases for $\varvec{v}_{0}^{(i+1)}$, which are grouped below two by two (see Fig. 3.a). Invariant 1 is true for all cases. We show however by contradition that the first four cases (items 1.1 and 1.2) are not possible because otherwise, Invariant 2’ is not true:

• 1.1 Let us assume that $\varvec{v}_{0}^{(i+1)} = \varvec{v}_{l}^{(i)} + \varvec{m}_{0}^{(i)}, l \in \{1,2\}$. In these cases, ${\mathcal {T_\infty }}^{(i+1)}$ is adjacent to ${\mathcal {T_\infty }}^{(i)}$ along facet $(\varvec{q}, \varvec{v}_{1}^{(i)}, \varvec{v}_{2}^{(i)})$. We conclude that the interior of ${\mathcal {T_\infty }}^{(i+1)}$ and ${\mathcal {T_\infty }}^{(i)}$ are disjoint and cannot both contains $\varvec{p}$, which raises a contradiction.

• 1.2 If we assume now that $\varvec{v}_{0}^{(i+1)} = \varvec{v}_{1}^{(i)} + \varvec{m}_{2}^{(i)}$ or $\varvec{v}_{0}^{(i+1)} = \varvec{v}_{2}^{(i)} + \varvec{m}_{1}^{(i)}$. In these cases, $\varvec{v}_{0}^{(i+1)}$ lies on the plane passing by $\varvec{q}$, $\varvec{v}_{1}^{(i)}$ and $\varvec{v}_{2}^{(i)}$. We conclude that the interior of ${\mathcal {T_\infty }}^{(i+1)}$ is empty and cannot contains $\varvec{p}$, a contradiction.

• 1.3 Hence, $\varvec{v}_{0}^{(i+1)} = \varvec{v}_{0}^{(i)} + \varvec{m}_{l}^{(i)}, l \in \{1,2\}$. In this case, ${\mathcal {T_\infty }}^{(i+1)}$, which contains ${\mathcal {T_\infty }}^{(i)}$, contains $\varvec{p}$.

We now assume that ${\mathbf {T}}^{(i)}$ and ${\mathbf {T}}^{(i+1)}$ share one vertex. Let us assume w.l.o.g. that its index is 2.

By definition, $\varvec{v}_{0}^{(i+1)},\varvec{v}_{1}^{(i+1)} \in \varSigma _{{\mathbf {T}}^{(i)}} \cap \mathbf {P}$. There are $\left( {\begin{array}{c}6\\ 2\end{array}}\right) = 15$ cases to consider for $\varvec{v}_{0}^{(i+1)}$ and $\varvec{v}_{1}^{(i+1)}$, which are grouped below into four different items. See Fig. 3.b for the last three items. Invariant 1 is true for all cases. We show however that Invariant 2 is true for only the three cases described at item 2.3:

• 2.0 (3 cases) Let us assume that $\varvec{v}_{0}^{(i+1)}$ and $\varvec{v}_{1}^{(i+1)}$ are opposite with respect to $\varvec{q}$, i.e. one is equal to $\varvec{q}+\varvec{d}_{k}^{(i+1)}$, $k {~\in \{0,1,2\}}$, whereas the other is equal to $\varvec{q}-\varvec{d}_{k}^{(i+1)}$. Since $\varvec{q}\notin \mathbf {P}$, $\varvec{q}+\varvec{d}_{k}^{(i+1)}$ and $\varvec{q}-\varvec{d}_{k}^{(i+1)}$ cannot be both in $\mathbf {P}$ by linearity, which raises a contradiction.

• 2.1 (7 cases) Let us assume that $\varvec{v}_{0}^{(i+1)} = \varvec{v}_{2}^{(i)} + \varvec{m}_{l}^{(i)}, l \in \{1,2\}$ or $\varvec{v}_{1}^{(i+1)} = \varvec{v}_{2}^{(i)} + \varvec{m}_{l}^{(i)}, l \in \{1,2\}$. In all cases, ${\mathcal {T_\infty }}^{(i+1)}$ is adjacent to ${\mathcal {T_\infty }}^{(i)}$ by edge $(\varvec{q}, \varvec{v}_{2}^{(i)})$, by facet $(\varvec{q}, \varvec{v}_{0}^{(i)}, \varvec{v}_{2}^{(i)})$ or by facet $(\varvec{q}, \varvec{v}_{1}^{(i)}, \varvec{v}_{2}^{(i)})$. As a consequence, the interior of ${\mathcal {T_\infty }}^{(i+1)}$ cannot contains $\varvec{p}$.

• 2.2 (2 cases) Let us assume that $\varvec{v}_{0}^{(i+1)} = \varvec{v}_{l}^{(i)} + \varvec{m}_{l+1}^{(i)}$ and $\varvec{v}_{1}^{(i+1)} = \varvec{v}_{l}^{(i)} + \varvec{m}_{l+2}^{(i)}$, for $l \in \{0,1\}$. In both cases, ${\mathcal {T_\infty }}^{(i+1)}$ is adjacent to ${\mathcal {T_\infty }}^{(i)}$ by edge $(\varvec{q}, \varvec{v}_{l}^{(i)})$. As a consequence, the previous argument also applies.

• 2.3 (3 cases) ${\mathcal {T_\infty }}^{(i+1)}$ contains ${\mathcal {T_\infty }}^{(i)}$ and thus contains $\varvec{p}$ in the following cases: $\varvec{v}_{0}^{(i+1)} = \varvec{v}_{0}^{(i)} + \varvec{m}_{l_0}^{(i)}, l_0 \in \{1,2\}$ and $\varvec{v}_{1}^{(i+1)} = \varvec{v}_{1}^{(i)} + \varvec{m}_{l_1}^{(i)}, l_1 \in \{0,2\}$, with $(l_0,l_1) \ne (1,0)$.    $\square$

Lemma 3

Let $\mathbf {M}^{(i)}$ be the $3\times 3$ matrix that consists of the three row vectors $(\varvec{m}_{k}^{(i)})_{k {~\in \{0,1,2\}}}$. Then, ${\forall i \in \{0,\dots ,n\}}, \ \det {(\mathbf {M}^{(i)})} = 1$.

Proof

We can easily check that $\det {(\mathbf {M}^{(0)})} = 1$.

We now prove that if $\det {(\mathbf {M}^{(i)})} = 1$ for ${i \in \{0,\dots ,n-1\}}$, then $\det {(\mathbf {M}^{(i+1)})} = 1$. By Lemmas 1 and 2, we have $\varvec{v}_{k}^{(i+1)} = \varvec{v}_{k}^{(i)} + \varvec{m}_{l}^{(i)} \Leftrightarrow \varvec{m}_{k}^{(i+1)} = \varvec{m}_{k}^{(i)} - \varvec{m}_{l}^{(i)}, l \ne k$ for at most two rows over three, while the remaining one or two rows correspond to identity. Such matrix operations do not change the determinant, which concludes.    $\square$

3.3 Termination

In the following proofs, we compare the position of the points along direction $\mathbf {N}$. For the sake of simplicity, we use the bar notation $\overline{\cdot }$ above any vector $\varvec{x}$ to denote its height relative to $\mathbf {N}$. Otherwise said, $\overline{\varvec{x}}:= \varvec{x}\cdot \mathbf {N}$. Even if $\mathbf {N}$ is not known, $\overline{\varvec{q}}\ge \omega$ by definition and for all $\varvec{x}\in \mathbf {P}$, $0 \le \overline{\varvec{x}}< \omega$.

Theorem 1

The number of steps in Algorithm 1 is bounded from above by $\omega -3$.

Proof

First, it is easy to see that $\forall k, \varvec{m}_{k}^{(0)} = \varvec{e}_{k+2}$. Thus, $\sum _k \overline{\varvec{m}}_{k}^{(0)} = \omega$.

Let us recall that ${\forall i \in \{0,\dots ,n\}},\ \forall k, \ \varvec{m}_{k}^{(i)} = \varvec{q}- \varvec{v}_{k}^{(i)}$. We have $\overline{\varvec{q}}\ge \omega$ by definition of $\varvec{q}$ and ${\forall i \in \{0,\dots ,n\}}, \ \forall k, \ 0 \le \overline{\varvec{v}}_{k}^{(i)} < \omega$ by Invariant 1 and by definition of $\mathbf {P}$. As a consequence, ${\forall i \in \{0,\dots ,n\}}, \ \forall k, \ \overline{\varvec{m}}_{k}^{(i)} > 0$ and $\sum _k \overline{\varvec{m}}_{k}^{(i)} \ge ~3$.

Moverover, by Lemma 2 and since any $\overline{\varvec{m}}_{k}^{(i)}$ is strictly positive ${\forall i \in \{0,\dots ,n\}}$, we clearly have ${\forall i \in \{0,\dots ,n-1\}}, \ \sum _k \overline{\varvec{m}}_{k}^{(i)} > \sum _k \overline{\varvec{m}}_{k}^{(i+1)}$.

The sequence $( \sum _k \overline{\varvec{m}}_{k}^{(i)} )_{i=0,\dots ,n}$ is thus a strictly decreasing sequence of integers between $\omega$ and 3.    $\square$

Remark that this bound is reached when running the algorithm on a plane with normal $\mathbf {N}(1,1,r)$. We now give the main result when the starting point $\varvec{p}$ is a lower leaning point, i.e. $\overline{\varvec{p}}= 0$. Note that in this case $\overline{\varvec{q}}= \omega$. Since we focus below on the last step n, we omit the exponent (n) in the proofs to improve their readability.

Theorem 2

If $\varvec{p}$ is a lower leaning point (i.e. $\overline{\varvec{p}}=0$ and thus $\overline{\varvec{q}}=\omega$), the vertices of the last triangle are upper leaning points, i.e. $\forall k, \overline{\varvec{v}}_{k}^{(n)} = \omega -1$.

Proof

If there exists $k {~\in \{0,1,2\}}$ such that $\overline{\varvec{d}}_{k} \ne 0$, then either (i) $\overline{\varvec{d}}_{k} < 0$ or (ii) $\overline{\varvec{d}}_{k} > 0$. Since $\overline{\varvec{q}}= \omega$ and $|\overline{\varvec{d}}_{k}| < \omega$, either (i) $\varvec{q}+ \varvec{d}_{k} \in \mathbf {P}$ or (ii) $\varvec{q}- \varvec{d}_{k} \in \mathbf {P}$. This implies that $\varSigma _{\mathbf {T}} \cap \mathbf {P}\ne \emptyset$, which is a contradiction because $\varSigma _{\mathbf {T}} \cap \mathbf {P}= \emptyset$ at the last step (see Algorithm 1, l. 2). As a consequence, $\forall k, \overline{\varvec{d}}_{k} = 0$ and $\forall k, \overline{\varvec{m}}_{k} = \alpha$, a strictly positive integer.

Let us denote by $\mathbf {1}$ the vector $(1,1,1)^T$. We can write the last system as $\mathbf {M}\mathbf {N}= \alpha \mathbf {1}$. Since $\mathbf {M}$ is invertible (because $\det {(\mathbf {M}}) = 1$ by Lemma 3), $\mathbf {N}= \mathbf {M}^{-1} \alpha \mathbf {1}$ and as a consequence $\alpha = 1$ (because the components of $\mathbf {N}$ are relatively prime and $\mathbf {M}^{-1}$ is unimodular).

We conclude that $\forall k, \overline{\varvec{m}}_{k} = 1$ and, straightforwardly, $\overline{\varvec{v}}_{k} = \omega - 1$.    $\square$

The following two corollaries are easily derived from Lemma 3 and Theorem 2.

Corollary 1

If $\varvec{p}$ is a lower leaning point, the normal of the last triangle is equal to $\mathbf {N}$, i.e. $\mathbf {\hat{N}}({\mathbf {T}}^{(n)}) = \mathbf {N}$.

Corollary 2

If $\varvec{p}$ is a lower leaning point, $(\varvec{d}_{0}^{(n)}, \varvec{d}_{1}^{(n)})$ is a basis of the lattice of upper leaning points $\{ \varvec{x}\in \mathbf {P}| \overline{\varvec{x}}= \omega - 1\}$.

4 Lattice Reduction and Delaunay Condition

Corollary 2 implies that the edge vectors of the last triangle form a basis of the lattice of upper leaning points to $\mathbf {P}$.

Let us recall that a basis $(\varvec{x},\varvec{y})$ is reduced if and only if $\Vert \varvec{x}\Vert , \Vert \varvec{y}\Vert \le \Vert \varvec{x}- \varvec{y}\Vert \le \Vert \varvec{x}+ \varvec{y}\Vert$. Given $(\varvec{x},\varvec{y})$ a basis of a two dimensional lattice, there is an iterative algorithm to compute a reduced basis from $(\varvec{x},\varvec{y})$. This algorithm consists in replacing the longest vector among $(\varvec{x},\varvec{y})$ by the shortest one among $\varvec{x}+\varvec{y}$ and $\varvec{x}-\varvec{y}$, if it is smaller.

We have found many examples for which the basis returned by Algorithm 1 is not reduced, even if we take the two shortest vectors in $\{\varvec{d}_{k}^{(n)}\}_{k {~\in \{0,1,2\}}}$ (see Fig. 4.a for an example). To cope with this problem, we can either apply the above reduction algorithm to the returned basis, or keep triangles as “small” as possible so that the last triangle leads to a reduced basis, without any extra reduction steps. To achieve this aim, we use a variant of Algorithm 1; see Algorithm 2.

Note that in Algorithm 2, we compute the convex hull of $T \cup S^\star$, but since $S^\star \subset \varSigma _{\mathbf {T}} \cap \mathbf {P}$ and since $\varSigma _{\mathbf {T}} \cap \mathbf {P}\ne \emptyset \Rightarrow S^\star \ne \emptyset$, all the results of Sect. 3 remain valid.

In Fig. 4, the results of the two algorithms for the digital plane of normal (2, 3, 9) are compared. The triangles returned by Algorithm 2 are more compact and closer to segment $[\varvec{p}\varvec{q}]$. The last triangle returned by Algorithm 2 leads to a reduced basis, but this is not true for Algorithm 1.

Fig. 4.

Triangles returned by Algorithm 1 in (a) and Algorithm 2 in (b) for a digital plane with normal (2, 3, 9) (the corner point $\varvec{p}$ is set to the origin). In (b), triangles returned by Algorithm 2 are smaller and the last one defines a reduced basis.

Algorithm	Algorithm 1	Algorithm 2
avg. nb. steps	21.8	20.9
nb. non-reduced	4803115 (73 %)	924 (0.01 %)
avg. nb. reductions	5.5	1

In practice, Algorithm 2 drastically reduces the cases of non-reduced basis. We have compared the two variants for normal vectors ranging from (1, 1, 1) to (200, 200, 200). There are 6578833 vectors with relatively prime components in this range. It turns out that less than 0.01 % of the basis returned by Algorithm 2 are non-reduced against about 73 % for Algorithm 1.

5 Applications to Digital Surfaces

In this section, we consider a set of voxels, Z, where voxels are seen as unit cubes whose vertices are in ${\mathbb {Z}}^3$. The digital boundary, $\mathrm {Bd}Z$, is defined as the topological boundary of Z. Since a digital boundary looks locally like a digital plane, it is natural to run our algorithm at each reentrant corner of the digital boundary with predicate “Is $\varvec{x}$ in $\mathrm {Bd}Z$” in order to estimate the local normal vector to the volume Z (see Fig. 5).

Fig. 5.

Our algorithm has been runned at each reentrant corner of a digital plane (left) and an ellipse (right). The last triangle of each run is printed.

Although we do not go into details here due to space limitations, we can mention the following points:

• Our algorithm works well on digitally convex shapes Z. The set of points $\varvec{x}\in \mathrm {Bd}Z$ located below some facet $\mathcal {F}$ of $\mathrm {Conv}(\mathrm {Bd}Z)$ whose normal vector is in the first octant and such that points $\varvec{x}+\varvec{s}$ are strictly above $\mathcal {F}$, is a piece of a digital plane, $\mathbf {P}$. If the starting reentrant corner is a lower leaning point of $\mathbf {P}$, the last triangle computed by our algorithm is included in $\mathcal {F}$ (see Fig. 5). We call such triangles patterns of $\mathbf {P}$.

• When starting from a corner that is not a lower leaning point of a facet of $\mathrm {Conv}(\mathrm {Bd}Z)$, the algorithm returns a triangle called reduced pattern of $\mathbf {P}$ which is approximately aligned with the plane.

• It is possible to detect and remove reduced patterns with a simple algorithm. Put in queue every point $\varvec{q}$ of all computed triangles, together with their three vectors $\varvec{m}_{k}$. Loop on the queue while it is not empty by popping them in sequence. For each popped point $\varvec{q}$ and vectors $\varvec{m}_{k}$, check if $\varvec{q}$ translated by any of $\varvec{m}_{k}$ is a shifted point $\varvec{q}'$ of another triangle. In this case, mark $\varvec{q}'$ as reduced pattern and put it back in queue but now with the vectors $\varvec{m}_{k}$. Otherwise, do nothing. When the algorithm stops, since reduced patterns have shifted points above the shifted point of the lower leaning point, all reduced patterns are marked.

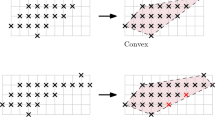
• If the shape is not convex, the algorithm can be adapted to detect planarity defects. The idea is that $\varSigma _{\mathbf {T}} \cap \mathrm {Bd}Z$ should contain at most three elements if it is locally a piece of plane. Moreover these elements must always be consecutive neighbors around $\varvec{q}$ in $\varSigma _{\mathbf {T}}$. We thus stop the algorithm whenever at least one of the two previous conditions fails, meaning that the surface is locally non convex. We also check that each new triangle is separating onto the digital boundary: for any point $\varvec{x}\in \mathrm {Bd}Z$ below a triangle of shift $\varvec{s}$, the point $\varvec{x}+\varvec{s}$ must be above the triangle.

6 Conclusion and Perspectives

In this paper, we proposed a new algorithm that computes the parameters of a digital plane. In opposition to usual plane recognition algorithms, this algorithm greedily decides on-the-fly which points have to be considered like in [7]. Compared to [7], this algorithm is however simpler because it consists in iterating one geometrical operation, which is fully characterized in Lemma 2. In addition, the returned solution, which is described by a triangle parallel to the sought plane, is close to the starting point. On one hand, the starting point must projects onto the triangle and on the other hand, the two shortest edge vectors of the triangle almost always form a reduced basis (in the second version of our algorithm).

For the future, we would like to find a theoretically sound way of always getting a reduced basis, without any extra reduction operation. Moreover, we would like to find a variant of our algorithm in order to retrieve complement triangles whose Bezout point is not above the triangle. For sake of completeness, we are also interested in degenerate cases, where at least one component is null. After having achieved these goals, we would have a complete working tool for the analysis of digitally convex surfaces. In order to correctly process concave or saddle parts however, we must precisely associate to a given triangle a piece of digital plane containing the triangle vertices and having the same normal vector than the triangle one. Although there are many such pieces of digital plane for a given triangle, we hope that this work will provide a canonical hierarchy of pieces of digital plane.