Abstract
We present a survey of some results and questions related to the notion of scalar curvature in the setting of symplectic supermanifolds.
Jaime Muñoz-Masqué, maestro y amigo, en su 65 aniversario
Dedicated to Muñoz-Masqué, teacher and friend, on his 65th birth anniversary.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
This is not a great loss of generality in view of the existence of the vector bundle isomorphism \({\textit{TM}}\rightarrow E\), between \({\textit{TM}}\) and the Batchelor bundle, already mentioned in the Introduction (see [13]), so the changes needed to deal with the most general case are mainly notational.
- 2.
In a technical sense that we will not describe here. See [12] for the details.
- 3.
In particular,
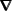 is not a tensor, hence the difference in notation.
is not a tensor, hence the difference in notation.
References
Batalin, I.A., Bering, K.: Odd scalar curvature in field-antifield formalism. J. Math. Phys. 49, 033515 (2008)
Batalin, I.A., Bering, K.: Odd scalar curvature in anti-Poisson geometry. Phys. Lett. B 663(1–2), 132–135 (2008)
Blaga, P.A.: Symplectic connections on supermanifolds: existence and non-uniqueness. Studia Univ. Babes-Bolyai Math. 58(4), 477–483 (2013)
De Castro, A., Martín, I., Quevedo, L., Restuccia, A.: Noncommutative associative superproduct for general supersymplectic forms. J. High Energy Phys. 0808, 009 (2008)
Fedosov, B.V.: A simple geometrical construction of deformation quantization. J. Diff. Geom. 40(2), 213–238 (1997)
Frlicher, A., Nijenhuis, A.: Theory of vector valued differential forms. Part I. Indag. Math. 18, 338–360 (1956)
Gelfand, I., Retakh, V., Shubin, M.: Fedosov manifolds. Adv. Math. 136(1), 104–140 (1998)
Geyer, B., Lavrov, P.M.: Fedosov supermanifolds: basic properties and the difference in even and odd cases. Int. J. Modern Phys. A 19, 3195 (2004)
Hernández-Amador, R.: Ph.D. Thesis, Universidad de Sonora, México, in preparation (2015)
Jacobson, T., Smolin, L.: The left-handed spin connection as a variable for canonical gravity. Phys. Lett. B 196, 39–42 (1987)
Kosmann-Schwarzbach, Y., Monterde, J.: Divergence operators and odd Poisson brackets. Ann. Inst. Fourier 52, 419–456 (2002)
Kostant, B.: Graded manifolds, graded Lie theory, and prequantization. Differential Geometrical Methods in Mathematical Physics. Lecture Notes in Mathematics, vol. 570, pp. 177–306 (1977)
Monterde, J.: A characterization of graded symplectic structures. Diff. Geom. Appl. 2, 81–97 (1992)
Monterde, J., Muñoz-Masqué, J., Vallejo, J.A.: The structure of Fedosov supermanifolds. J. Geom. Phys. 59, 540–553 (2009)
Salgado, G., Vallejo, J.A.: The meaning of time and covariant superderivatives in supermechanics. Adv. Math. Phys. (2009) Article ID 987524
Vallejo, J.A.: Symplectic connections and Fedosov’s quantization on supermanifolds. J. Phys. Conf. Ser. 343, 012124 (2012)
Acknowledgments
JM was supported by a Spanish Ministry of Science and Innovation project code MTM2012-33073. JV was supported by a CONACyT (México) project code CB-2012-179115.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Hernández-Amador, R., Monterde, J., Vallejo, J. (2016). Supermanifolds, Symplectic Geometry and Curvature. In: Castrillón López, M., Hernández Encinas, L., Martínez Gadea, P., Rosado María, M. (eds) Geometry, Algebra and Applications: From Mechanics to Cryptography. Springer Proceedings in Mathematics & Statistics, vol 161. Springer, Cham. https://doi.org/10.1007/978-3-319-32085-4_12
Download citation
DOI: https://doi.org/10.1007/978-3-319-32085-4_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-32084-7
Online ISBN: 978-3-319-32085-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


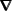 is not a tensor, hence the difference in notation.
is not a tensor, hence the difference in notation.