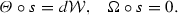Abstract
We provide a pedagogical introduction to the method of holographic renormalization, in its Hamiltonian incarnation. We begin by reviewing the description of local observables, global symmetries, and ultraviolet divergences in local quantum field theories, in a language that does not require a weak coupling Lagrangian description. In particular, we review the formulation of the Renormalization Group as a Hamiltonian flow, which allows us to present the holographic dictionary in a precise and suggestive language. The method of holographic renormalization is then introduced by first computing the renormalized two-point function of a scalar operator in conformal field theory and comparing with the holographic computation. We then proceed with the general method, formulating the bulk theory in a radial Hamiltonian language and deriving the Hamilton–Jacobi equation. Two methods for solving recursively the Hamilton–Jacobi equation are then presented, based on covariant expansions in eigenfunctions of certain functional operators on the space of field theory couplings. These algorithms constitute the core of the method of holographic renormalization and allow us to obtain the holographic Ward identities and the asymptotic expansions of the bulk fields.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Sometimes, additional global observables must be specified to uniquely identify a theory [14].
- 2.
To make contact with [16] one can introduce a Hamiltonian density,
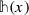 , through
, through 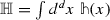 .
. - 3.
Note that in [16] only the RG invariant \(W_\mathrm{ren}[J;\tau ]\) is considered, written in terms of the bare and renormalized couplings. W[J] is not discussed at all in that reference.
- 4.
The way we have defined the operators \(\mathcal{O}_\alpha \) and \(\mathbb H\) in this subsection, they are in fact densities with respect to the background metric \(g_{ij}\), i.e. we have not divided by \(\sqrt{g}\) as in (9). Moreover, \(\mathcal{O}_\alpha \) include the stress tensor.
- 5.
The subscript (0) here is intended to help make contact with the holographic computation later.
- 6.
- 7.
In order to distinguish them from arbitrary integration functions of the HJ partial differential equation, we refer to arbitrary functions of the transverse coordinates arising from the integration of the radial equations of motion as “integration constants”.
- 8.
Since under certain conditions both modes can be normalizable, more generally the distinction is between asymptotically subleading and dominant modes, respectively.
- 9.
For the gravity-scalar system the expansion in eigenfunctions of (109) is indeed a derivative expansion. However, in general this is not the case. A counterexample is a Maxwell field.
- 10.
The overall sign of U is determined by requiring that the first order equations (96) imply the correct leading asymptotic behavior for the scalar, namely \(\varphi \sim e^{-(d-\varDelta )r}\). Moreover, when the scalar mass saturates the BF bound, one of the two asymptotic solutions for \(U(\varphi )\) contains logarithms. We refer to [39] for the explicit form of the function \(U(\varphi )\) in that case.
- 11.
- 12.
Note that the scalar field here is rescaled by a factor of \(\sqrt{2\kappa ^2}\) relative to the scalar in (83).
- 13.
Note one needs to adjust these for the different normalization of the scalar.
- 14.
In this appendix a dot \(\,\dot{}\,\) denotes a derivative with respect to time t.
References
J.M. Maldacena, The large N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 38, 1113–1133 (1999). arXiv:hep-th/9711200 [Adv. Theor. Math. Phys. 2, 231(1998)]
E. Witten, Anti-de Sitter space and holography. Adv. Theor. Math. Phys. 2, 253–291 (1998). arXiv:hep-th/9802150
S. Gubser, I.R. Klebanov, A.M. Polyakov, Gauge theory correlators from noncritical string theory. Phys. Lett. B 428, 105–114 (1998). arXiv:hep-th/9802109
M. Henningson, K. Skenderis, The holographic Weyl anomaly. J. High Energy Phys. 07, 023 (1998). arXiv:hep-th/9806087
V. Balasubramanian, P. Kraus, A stress tensor for Anti-de Sitter gravity. Commun. Math. Phys. 208, 413–428 (1999). arXiv:hep-th/9902121
J. de Boer, E.P. Verlinde, H.L. Verlinde, On the holographic renormalization group. J. High Energy Phys. 08, 003 (2000). arXiv:hep-th/9912012
P. Kraus, F. Larsen, R. Siebelink, The gravitational action in asymptotically AdS and flat space-times. Nucl. Phys. B 563, 259–278 (1999). arXiv:hep-th/9906127
S. de Haro, S.N. Solodukhin, K. Skenderis, Holographic reconstruction of space-time and renormalization in the AdS/CFT correspondence. Commun. Math. Phys. 217, 595–622 (2001). arXiv:hep-th/0002230
M. Bianchi, D.Z. Freedman, K. Skenderis, How to go with an RG flow. J. High Energy Phys. 08, 041 (2001). arXiv:hep-th/0105276
M. Bianchi, D.Z. Freedman, K. Skenderis, Holographic renormalization. Nucl. Phys. B 631, 159–194 (2002). arXiv:hep-th/0112119
D. Martelli, W. Mueck, Holographic renormalization and ward identities with the Hamilton-Jacobi method. Nucl. Phys. B 654, 248–276 (2003). arXiv:hep-th/0205061
K. Skenderis, Lecture notes on holographic renormalization. Class. Quantum Gravity 19, 5849–5876 (2002). arXiv:hep-th/0209067
I. Papadimitriou, K. Skenderis, AdS/CFT correspondence and geometry, AdS/CFT correspondence: Einstein metrics and their conformal boundaries. Proceedings, 73rd Meeting of Theoretical Physicists and Mathematicians, Strasbourg, France, 11–13 September 2003 (2004), pp. 73–101. arXiv:hep-th/0404176
O. Aharony, N. Seiberg, and Y. Tachikawa, Reading between the lines of four-dimensional gauge theories, JHEP 08 (2013) 115, 1305.0318
H. Osborn, Weyl consistency conditions and a local renormalization group equation for general renormalizable field theories. Nucl. Phys. B 363, 486–526 (1991)
B.P. Dolan, Symplectic geometry and Hamiltonian flow of the renormalization group equation. Int. J. Mod. Phys. A 10, 2703–2732 (1995). arXiv:hep-th/9406061
I. Papadimitriou, Holographic renormalization as a canonical transformation. J. High Energy Phys. 11, 014 (2010). arXiv:1007.4592
D.Z. Freedman, K. Johnson, J.I. Latorre, Differential regularization and renormalization: a new method of calculation in quantum field theory. Nucl. Phys. B 371, 353–414 (1992)
I. Papadimitriou, Holographic renormalization made simple: an example. Subnucl. Ser. 41, 508–514 (2005)
G.W. Gibbons, S.W. Hawking, Action integrals and partition functions in quantum gravity. Phys. Rev. D 15, 2752–2756 (1977)
I. Papadimitriou, K. Skenderis, Thermodynamics of asymptotically locally AdS spacetimes. J. High Energy Phys. 08, 004 (2005). arXiv:hep-th/0505190
R. Arnowitt, S. Deser, C.W. Misner, Canonical variables for general relativity. Phys. Rev. 117, 1595–1602 (1960)
I. Papadimitriou, Multi-trace deformations in AdS/CFT: exploring the vacuum structure of the deformed CFT. J. High Energy Phys. 05, 075 (2007). arXiv:hep-th/0703152
M. Henneaux, C. Teitelboim, Quantization of Gauge Systems (University of Princeton, Princeton, 1992)
B. C. van Rees, Holographic renormalization for irrelevant operators and multi-trace counterterms. Physics 42 (2011). arXiv:1102.2239
B.C. van Rees, Irrelevant deformations and the holographic Callan-Symanzik equation. J. High Energy Phys. 10, 067 (2011). arXiv:1105.5396
K.A. Intriligator, Maximally supersymmetric RG flows and AdS duality. Nucl. Phys. B 580, 99–120 (2000). arXiv:hep-th/9909082
K. Skenderis, M. Taylor, Kaluza-Klein holography. J High Energy Phys. 05, 057 (2006). arXiv:hep-th/0603016
K. Skenderis, M. Taylor, Holographic Coulomb branch vevs. J. High Energy Phys. 08, 001 (2006). arXiv:hep-th/0604169
Y. Korovin, K. Skenderis, M. Taylor, Lifshitz as a deformation of Anti-de Sitter. J. High Energy Phys. 08, 026 (2013). arXiv:1304.7776
W. Chemissany, I. Papadimitriou, Lifshitz holography: the whole shebang. J. High Energy Phys. 01, 052 (2015). arXiv:1408.0795
A. O’Bannon, I. Papadimitriou, J. Probst, A Holographic Two-Impurity Kondo Model. arXiv:1510.08123
S.F. Ross, Holography for asymptotically locally Lifshitz spacetimes. Class. Quantum Gravity 28, 215019 (2011). arXiv:1107.4451
T. Griffin, P. Horava, C.M. Melby-Thompson, Conformal Lifshitz gravity from holography. J. High Energy Phys. 05, 010 (2012). arXiv:1112.5660
I. Papadimitriou, Holographic renormalization of general dilaton-axion gravity. J High Energy Phys. 1108, 119 (2011). arXiv:1106.4826
W. Chemissany, I. Papadimitriou, Generalized dilatation operator method for non-relativistic holography. Phys. Lett. B 737, 272–276 (2014). arXiv:1405.3965
I. Kanitscheider, K. Skenderis, M. Taylor, Precision holography for non-conformal branes. J. High Energy Phys. 09, 094 (2008). arXiv:0807.3324
P. Breitenlohner, D.Z. Freedman, Positive energy in anti-De Sitter backgrounds and gauged extended supergravity. Phys. Lett. B 115, 197 (1982)
I. Papadimitriou, K. Skenderis, Correlation functions in holographic RG flows. J. High Energy Phys. 0410, 075 (2004). arXiv:hep-th/0407071
H.J. Rothe, K.D. Rother, Classical and Quantum Dynamics of Constrained Hamiltonian Systems (World Scientific, Singapore, 2010)
R. Abraham, J. Marsden, Foundations of Mechanics, 2nd edn. (Benjamin-Cumming, Reading, 1978)
M. de Leon, J.C. Marrero, D.M. de Diego, A geometric Hamilton-Jacobi theory for classical field theories (2008). arXiv:0801.1181
Acknowledgments
I would like to thank the International Institute of Physics, Natal, for the hospitality and financial support during the School on Theoretical Frontiers in Black Holes and Cosmology, June 8–19, 2015, where these lectures were delivered.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix
ADM Identities
A few identities relating to the ADM decomposition (84) of the metric are collected in this appendix. In particular, in matrix form, the metric (84) and its inverse are
where the indices \(i=1,\ldots ,d\) are raised and lowered respectively with \(\gamma ^{ij}\) and \(\gamma _{ij}\). Moreover, the Christoffel symbols \(\varGamma ^\rho _{\mu \nu }[g]\) can be decomposed into the following components in terms of N, \(N_i\) and \(\gamma _{ij}\):
Hamilton–Jacobi Primer
In this appendix we collect a few essential facts about HJ theory in classical mechanics. For an in-depth account of HJ theory we refer the interested reader to [24, 40]. A more abstract exposition can be found in [41].
Let \(\mathcal{Q}\) be the configuration space of a point particle described by the actionFootnote 14
where \(q^\alpha \) are coordinates on \(\mathcal{Q}\). In the Hamiltonian formalism the generalized coordinates \(q^\alpha \) and the canonical momenta
are independent variables parameterizing the phase space, which is isomorphic to the cotangent bundle \(T^*\mathcal{Q}\) of the configuration space \(\mathcal{Q}\). The cotangent bundle is a symplectic manifold with a canonical closed 2-form (symplectic form)
Since  is closed, it can be locally expressed as
is closed, it can be locally expressed as

where
is known as the canonical 1-form, or pre-symplectic form. The Hamiltonian, given by the Legendre transform of the Lagrangian,
is a map \(H:T^*\mathcal{Q}\longrightarrow \mathbb {R}\) and governs the time evolution of the dynamical system through Hamilton’s equations
At this point it is instructive to distinguish two cases, depending on whether the Hamiltonian depends explicitly on time t or not.
-
Time-independent systems
A section, s, of the cotangent bundle is a map \(s:\mathcal{Q}\longrightarrow T ^*\mathcal{Q}\), providing a 1-form over each point \(q\in \mathcal{Q}\). A closed section of \(T^*\mathcal{Q}\) is locally exact and so it can be written as \(s=d\mathcal{W}\) for some function \(\mathcal{W}(q)\) on \(\mathcal{Q}\). Under the isomorphism between phase space and the cotangent bundle this means that locally
$$\begin{aligned} p_\alpha =\frac{\partial \mathcal{W}(q)}{\partial q^\alpha }. \end{aligned}$$(199)Moreover,
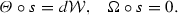 (200)
(200)These results hold for any closed section s of \(T^*\mathcal{Q}\). The HJ theorem relates certain closed sections, s, of the cotangent bundle to solutions of Hamilton’s equations (198). In particular,
$$\begin{aligned} d\left( H\circ s\right)&=\left( \frac{\partial H}{\partial q^\alpha }+\frac{\partial ^2\mathcal{W}}{\partial q^\beta \partial q^\alpha }\frac{\partial H}{\partial p_\beta }\right) dq^\alpha \nonumber \\&=\left( \frac{\partial H}{\partial q^\alpha }+\dot{p}^\alpha \right) dq^\alpha +\frac{\partial ^2\mathcal{W}}{\partial q^\beta \partial q^\alpha }\left( \frac{\partial H}{\partial p_\beta }-\dot{q}^\beta \right) dq^\alpha , \end{aligned}$$(201)which implies that the following two statements are equivalent (see Theorem 2.1 in [42]):
-
(i)
If \(\sigma :\mathbb {R}\rightarrow \mathcal{Q}\) satisfies the first of Hamilton’s equations in (198), then \(s\circ \sigma \) satisfies the second Hamilton equation.
-
(ii)
\(d\left( H\circ s\right) =0\).
Hence, a closed section \(s=d\mathcal{W}\) of the cotangent bundle that satisfies the (time-independent) HJ equation
$$\begin{aligned} H\circ s=H\left( \frac{\partial \mathcal{W}}{\partial q^\alpha },q^\beta \right) =E, \end{aligned}$$(202)where E is some constant, provides a solution of Hamilton’s equations.
-
(i)
-
Time-dependent systems
In order to accommodate systems with a Hamiltonian that explicitly depends on time we extend the configuration space by including time as a generalized coordinate so that \(\mathcal{Q}_\mathrm{ext}=\mathcal{Q}\times \mathbb {R}\) is now the extended configuration space. Phase space is accordingly extended by including \(-H\) as the canonical momentum conjugate to t. This extended phase space is isomorphic to the cotangent bundle \(T^*\mathcal{Q}_\mathrm{ext}\), which carries the canonical symplectic form
$$\begin{aligned} {\Omega }_\mathrm{ext}=d\varTheta _\mathrm{ext}=dp_\alpha \wedge dq^\alpha -dH\wedge dt. \end{aligned}$$(203)Moreover, to Hamilton’s equations we can now append the equation
$$\begin{aligned} \dot{H}=\frac{\partial H}{\partial t}. \end{aligned}$$(204)A closed section of \(T^*\mathcal{Q}_\mathrm{ext}\) can be locally written as \(s=d\mathcal{S}\) for some function on \(\mathcal{Q}_\mathrm{ext}\), and consequently
$$\begin{aligned} p_\alpha =\frac{\partial \mathcal{S}(q;t)}{\partial q^\alpha },\quad -H=\frac{\partial \mathcal{S}(q;t)}{\partial t}, \end{aligned}$$(205)which imply that
$$\begin{aligned} \varTheta _\mathrm{ext}\circ s=d\mathcal{S},\quad {\Omega }_\mathrm{ext}\circ s=0. \end{aligned}$$(206)It follows that
$$\begin{aligned} 0&=d\left( H\circ s+\frac{\partial \mathcal{S}}{\partial t}\right) \nonumber \\&=\left[ \frac{\partial H}{\partial q^\alpha }+\dot{q}^\beta \frac{\partial ^2\mathcal{S}}{\partial q^\beta \partial q^\alpha }+\frac{\partial ^2\mathcal{S}}{\partial t\partial q^\alpha }+\frac{\partial ^2\mathcal{S}}{\partial q^\beta \partial q^\alpha }\left( \frac{\partial H}{\partial p_\beta }-\dot{q}^\beta \right) \right] dq^\alpha \nonumber \\&\quad +\left[ \frac{\partial H}{\partial t}+\dot{q}^\alpha \frac{\partial ^2\mathcal{S}}{\partial t\partial q^\alpha }+\frac{\partial ^2\mathcal{S}}{\partial t^2}+\frac{\partial ^2\mathcal{S}}{\partial q^\beta \partial t}\left( \frac{\partial H}{\partial p_\beta }-\dot{q}^\beta \right) \right] dt\nonumber \\&=\left[ \frac{\partial H}{\partial q^\alpha }+\dot{p}^\alpha +\frac{\partial ^2\mathcal{S}}{\partial q^\beta \partial q^\alpha }\left( \frac{\partial H}{\partial p_\beta }-\dot{q}^\beta \right) \right] dq^\alpha \nonumber \\&\quad +\left[ \frac{\partial H}{\partial t}-\dot{H}+\frac{\partial ^2\mathcal{S}}{\partial q^\beta \partial t}\left( \frac{\partial H}{\partial p_\beta }-\dot{q}^\beta \right) \right] dt, \end{aligned}$$(207)which allows us to generalize the HJ theorem to time-dependent Hamiltonians. Namely, a closed section \(s=d\mathcal{S}\) of \(T^*\mathcal{Q}_\mathrm{ext}\) that satisfies the HJ equation
$$\begin{aligned} H\circ s+\frac{\partial \mathcal{S}}{\partial t}=H\left( \frac{\partial \mathcal{S}}{\partial q^\alpha },q^\beta ;t\right) +\frac{\partial \mathcal{S}}{\partial t}=0, \end{aligned}$$(208)provides a solution to Hamilton’s equations.
A few comments are in order at this point. Firstly, note that the HJ formalism for time-dependent Hamiltonians reduces to that for time-independent Hamiltonians upon setting
The function \(\mathcal{S}(q;t)\) is known as Hamilton’s principal function, while \(\mathcal{W}(q)\) is called the characteristic function. Secondly, the expressions (94) for the canonical momenta and the Hamiltonian should be familiar from quantum mechanics. Indeed, Hamilton’s principal function \(\mathcal{S}(q;t)\) is related to the WKB wavefunction by

and so the expressions (94) are respectively the coordinate representation of the momentum operator and the identification of the Hamiltonian with the time evolution operator.
Finally, Hamilton’s principal function \(\mathcal{S}(q;t)\), defined as a solution of the HJ equation (208), is closely related to the on-shell action. To elucidate the relation, consider the action (192) on the semi-infinite line \((-\infty ,t]\). A general variation of the action (192) gives
To ensure that the variational principle implies the equations of motion we need to impose the boundary condition \(\delta q^\alpha =0\) at \(t'=t\). The on-shell action therefore becomes a function of the fixed but arbitrary boundary condition \(q^\alpha (t)\), namely \(S_{\text {on}\text {-}\text {shell}}(q;t)\), while
Moreover,
and so \(S_{\text {on}\text {-}\text {shell}}\) satisfies the HJ equation (208):
We therefore conclude that the on-shell action as a function of the arbitrary but fixed boundary condition q(t), \(S_{\text {on}\text {-}\text {shell}}(q;t)\), can be identified with Hamilton’s principal function \(\mathcal{S}(q;t)\). The fact that the on-shell action is a solution of the HJ equation is the fundamental reason for the critical role that HJ theory has in holographic renormalization.
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
Papadimitriou, I. (2016). Lectures on Holographic Renormalization. In: Kallosh, R., Orazi, E. (eds) Theoretical Frontiers in Black Holes and Cosmology. Springer Proceedings in Physics, vol 176. Springer, Cham. https://doi.org/10.1007/978-3-319-31352-8_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-31352-8_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-31351-1
Online ISBN: 978-3-319-31352-8
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


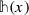 , through
, through 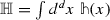 .
.