Abstract
Recently, a new notion of Geometric Semantic Genetic Programming emerged in the field of automatic program induction from examples. Given that the induction problem is stated by means of function learning and a fitness function is a metric, GSGP uses geometry of solution space to search for the optimal program. We demonstrate that a program constructed by GSGP is indeed a linear combination of random parts. We also show that this type of program can be constructed in a predetermined time by much simpler algorithm and with guarantee of solving the induction problem optimally. We experimentally compare the proposed algorithm to GSGP on a set of symbolic regression, Boolean function synthesis and classifier induction problems. The proposed algorithm is superior to GSGP in terms of training-set fitness, size of produced programs and computational cost, and generalizes on test-set similarly to GSGP.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
 for two Booleans is equivalent to \(\vee \), for two classes outputs the one with lower id, for a class and
for two Booleans is equivalent to \(\vee \), for two classes outputs the one with lower id, for a class and 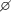 outputs this class, otherwise
outputs this class, otherwise  .
.  for two Booleans is equivalent to \(\wedge \), for two classes outputs the one with greater id, for 1 and a class outputs this class, otherwise
for two Booleans is equivalent to \(\wedge \), for two classes outputs the one with greater id, for 1 and a class outputs this class, otherwise 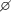 . We omitted full tables of these functions for brevity.
. We omitted full tables of these functions for brevity. - 2.
The distinction between linear combination and interpolation is made to emphasize that linear combination is any weighted sum of programs, while interpolation is a weighted sum that goes through the certain points.
- 3.
Points given by \(x_{k}=\frac{1}{2}(a+b)+\frac{1}{2}(b-a)\cos (\frac{2k-1}{2n}\pi ),k=1..n\), where [a, b] is the range of training set, and n is number of data points. Using Chebyshev nodes minimizes the likelihood of Runge’s phenomenon [29].
References
Burden, R., Faires, J.: Numerical Analysis. Cengage Learning (2010). http://books.google.pl/books?id=Dbw8AAAAQBAJ
Castelli, M., Castaldi, D., Giordani, I., Silva, S., Vanneschi, L., Archetti, F., Maccagnola, D.: An efficient implementation of geometric semantic genetic programming for anticoagulation level prediction in pharmacogenetics. In: Correia, L., Reis, L.P., Cascalho, J. (eds.) EPIA 2013. LNCS, vol. 8154, pp. 78–89. Springer, Heidelberg (2013)
Castelli, M., Henriques, R., Vanneschi, L.: A geometric semantic genetic programming system for the electoral redistricting problem. Neurocomputing 154, 200–207 (2015). http://www.sciencedirect.com/science/article/pii/S0925231214016671
Castelli, M., Vanneschi, L., Silva, S.: Prediction of high performance concrete strength using genetic programming with geometric semantic genetic operators. Expert Syst. Appl. 40(17), 6856–6862 (2013). http://www.sciencedirect.com/science/article/pii/S0957417413004326
Dershowitz, N., Jouannaud, J.P.: Rewrite systems. In: Handbook of Theoretical Computer Science. Formal Models and Sematics, vol. B, pp. 243–320 (1990)
Flach, P.: Machine Learning: The Art and Science of Algorithms that Make Sense of Data. Cambridge University Press, New York (2012)
Gentle, J.E.: Numerical Linear Algebra for Applications in Statistics. Statistics and Computing. Springer, New York (1998). http://opac.inria.fr/record=b1098288
Karnaugh, M.: The map method for synthesis of combinational logic circuits. Trans. Am. Inst. Electr. Eng. Part I: Commun. Electron. 72(5), 593–599 (1953)
Koza, J.R.: Genetic Programming: On the Programming of Computers by Means of Natural Selection. MIT Press, Cambridge (1992). http://mitpress.mit.edu/books/genetic-programming
Krawiec, K., Lichocki, P.: Approximating geometric crossover in semantic space. In: Raidl, G., et al. (eds.) Proceedings of the 11th Annual Conference on Genetic and Evolutionary Computation. GECCO 2009, pp. 987–994. ACM, Montreal, 8–12 July 2009
Krawiec, K., Pawlak, T.: Locally geometric semantic crossover: a study on the roles of semantics and homology in recombination operators. Genet. Program. Evolvable Mach. 14(1), 31–63 (2013)
Luke, S.: The ECJ Owner’s Manual - A User Manual for the ECJ Evolutionary Computation Library, zeroth edition, online version 0.2 (edn.), October 2010. http://cs.gmu.edu/eclab/projects/ecj/docs/
Mangasarian, O.L., Street, W.N., Wolberg, W.H.: Breast cancer diagnosis and prognosis via linear programming. Oper. Res. 43, 570–577 (1995)
McConaghy, T.: FFX: fast, scalable, deterministic symbolic regression technology. In: Riolo, R., Vladislavleva, E., Moore, J.H. (eds.) Genetic Programming Theory and Practice IX. Genetic and Evolutionary Computation, pp. 235–260. Springer, New York (2011). http://trent.st/content/2011-GPTP-FFX-paper.pdf
McDermott, J., Agapitos, A., Brabazon, A., O’Neill, M.: Geometric semantic genetic programmingfor financial data. In: Esparcia-Alcázar, A.I., Mora, A.M. (eds.) EvoApplications 2014. LNCS, vol. 8602, pp. 215–226. Springer, Heidelberg (2014)
McDermott, J., et al.: Genetic programming needs better benchmarks. In: Soule, T., et al. (eds.) Proceedings of the Fourteenth International Conference on Genetic and Evolutionary Computation Conference. GECCO 2012, pp. 791–798. ACM, Philadelphia, Pennsylvania, USA, 7–11 July 2012
Moraglio, A.: Abstract convex evolutionary search. In: Beyer, H.G., Langdon, W.B. (eds.) Foundations of Genetic Algorithms, pp. 151–162. ACM, Schwarzenberg, Austria, 5–9 January 2011
Moraglio, A., Krawiec, K., Johnson, C.G.: Geometric semantic genetic programming. In: Coello, C.A.C., Cutello, V., Deb, K., Forrest, S., Nicosia, G., Pavone, M. (eds.) PPSN 2012, Part I. LNCS, vol. 7491, pp. 21–31. Springer, Heidelberg (2012)
Moraglio, A., Mambrini, A.: Runtime analysis of mutation-based geometric semantic genetic programming for basis functions regression. In: Blum, C., et al. (eds.) Proceeding of the Fifteenth Annual Conference on Genetic and Evolutionary Computation Conference. GECCO 2013, pp. 989–996. ACM, Amsterdam, The Netherlands, 6–10 July 2013
Moraglio, A., Mambrini, A., Manzoni, L.: Runtime analysis of mutation-based geometric semantic genetic programming on boolean functions. In: Neumann, F., De Jong, K. (eds.) Foundations of Genetic Algorithms, pp. 119–132. ACM, Adelaide, Australia, 16–20 January 2013. http://www.cs.bham.ac.uk/axm322/pdf/gsgp_foga13.pdf
Moraglio, A., Sudholt, D.: Runtime analysis of convex evolutionary search. In: Soule, T., Moore, J.H. (eds.) GECCO, pp. 649–656. ACM (2012). http://dblp.uni-trier.de/db/conf/gecco/gecco2012.html#MoraglioS12
Nguyen, Q.U., Pham, T.A., Nguyen, X.H., McDermott, J.: Subtree semantic geometric crossover for genetic programming. Genet. Program. Evolvable Mach., 1–29. Online first
Pawlak, T.P.: Combining semantically-effective and geometric crossover operators for genetic programming. In: Bartz-Beielstein, T., Branke, J., Filipič, B., Smith, J. (eds.) PPSN 2014. LNCS, vol. 8672, pp. 454–464. Springer, Heidelberg (2014)
Pawlak, T.P.: Competent Algorithms for Geometric Semantic Genetic Programming. Ph.D. thesis, Poznan University of Technology, Poznan, Poland, 21 September 2015. http://www.cs.put.poznan.pl/tpawlak/link/?PhD
Pawlak, T.P., Krawiec, K.: Progress properties and fitness bounds for geometric semantic search operators. Genet. Program. Evolvable Mach., 1–19. Online first
Pawlak, T.P., Krawiec, K.: Guarantees of progress for geometric semantic genetic programming. In: Johnson, C., Krawiec, K., Moraglio, A., O’Neill, M. (eds.) Semantic Methods in Genetic Programming. Ljubljana, Slovenia 13 September 2014 (Workshop at Parallel Problem Solving from Nature 2014 Conference). http://www.cs.put.poznan.pl/kkrawiec/smgp2014/uploads/Site/Pawlak.pdf
Pawlak, T.P., Wieloch, B., Krawiec, K.: Review and comparative analysis of geometric semantic crossovers. Genet. Program. Evolvable Mach. 16(3), 351–386 (2015)
Pawlak, T.P., Wieloch, B., Krawiec, K.: Semantic backpropagation for designing search operators in genetic programming. IEEE Trans. Evol. Comput. 19(3), 326–340 (2015). http://dx.doi.org/10.1109/TEVC.2014.2321259
Runge, C.: Über empirische funktionen und die interpolation zwischen äquidistanten ordinaten. Z. Math. Phys. 46, 224–243 (1901)
Vanneschi, L., Silva, S., Castelli, M., Manzoni, L.: Geometric semantic genetic programming for real life applications. In: Riolo, R., Moore, J.H., Kotanchek, M. (eds.) Genetic Programming Theory and Practice XI. Genetic and Evolutionary Computation, pp. 191–209. Springer, Heidelberg (2013)
Zhu, Z., Nandi, A.K., Aslam, M.W.: Adapted geometric semantic genetic programming for diabetes and breast cancer classification. In: IEEE International Workshop on Machine Learning for Signal Processing (MLSP 2013), September 2013
Acknowledgements
This work is funded by National Science Centre Poland grant number DEC-2012/07/N/ST6/03066.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
Pawlak, T.P. (2016). Geometric Semantic Genetic Programming Is Overkill. In: Heywood, M., McDermott, J., Castelli, M., Costa, E., Sim, K. (eds) Genetic Programming. EuroGP 2016. Lecture Notes in Computer Science(), vol 9594. Springer, Cham. https://doi.org/10.1007/978-3-319-30668-1_16
Download citation
DOI: https://doi.org/10.1007/978-3-319-30668-1_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-30667-4
Online ISBN: 978-3-319-30668-1
eBook Packages: Computer ScienceComputer Science (R0)


 for two Booleans is equivalent to
for two Booleans is equivalent to 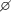 outputs this class, otherwise
outputs this class, otherwise  .
.  for two Booleans is equivalent to
for two Booleans is equivalent to 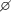 . We omitted full tables of these functions for brevity.
. We omitted full tables of these functions for brevity.