Abstract
We investigate the (multiagent) infinitary version \(\mathbf {K}_{\omega _1}\) of the propositional modal logic \(\mathbf {K}\), in which conjunctions and disjunctions over countably infinite sets of formulas are allowed. It is known that the natural infinitary extension \(\mathbf {LK}_{\omega _1}^{\Box }\) (here presented as a Tait-style calculus, \(\mathbf {TK}^{\sharp }_{\omega _1}\)) of the standard sequent calculus \(\mathbf {LK}_p^{\Box }\) for \(\mathbf {K}\) is incomplete with respect to Kripke semantics. It is also known that in order to axiomatize \(\mathbf {K}_{\omega _1}\) one has to add to \(\mathbf {LK}_{\omega _1}^{\Box }\) new initial sequents corresponding to the infinitary propositional counterpart \( BF _{\omega _1}\) of the Barcan Formula. We introduce a generalization of standard Kripke semantics, and prove that \(\mathbf {TK}^{\sharp }_{\omega _1}\) is sound and complete with respect to it. By the same proof strategy, we show that the stronger system \(\mathbf {TK}_{\omega _1}\), allowing countably infinite sequents, axiomatizes \(\mathbf {K}_{\omega _1}\), although it provably does not admit cut-elimination.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Alternatively, \( BF _{\omega _1}\) may be seen as an infinitary version of the \(\mathbf {K}\)-tautology \(\Box \varphi \wedge \Box \psi \rightarrow \Box (\varphi \wedge \psi )\).
- 2.
There is no special reason behind our choice of taking \(\widetilde{\Box }_i\) (where \(\Box \varphi \equiv \lnot \widetilde{\Box }_i\varphi \)) as a primitive operator in place of the more familiar \(\lozenge _i\) (where \(\Box _i \varphi \equiv \lnot \lozenge _i\lnot \varphi \)).
- 3.
In a classical environment, there is an obvious correspondence between two-sided and one-sided sequents. \(\text {`}\,\Gamma \Rightarrow \Delta \text {'}\;\rightsquigarrow \;\text {`}\,\lnot \Gamma , \Delta \text {'},\) and \(\text {`}\,\Gamma \text {'}\;\rightsquigarrow \;\text {`}\,\lnot \Gamma _1\Rightarrow \Gamma _2\text {'}\) for each partition \((\Gamma _1,\Gamma _2)\) of \(\Gamma \).
- 4.
Where formulas are of course intended to belong to the \(\Box _i\)- and \(\widetilde{\Box }_i\)-less fragment \(\mathcal {L}_{\omega _1}\) of \(\mathcal {L}^{\Box }_{\omega _1}\). Caution: in all the calculi under consideration in this paper sequents are sets, not multisets. This means that contraction is hidden in the logical inference rules: the principal formula of an inference may occur as a side formula in the premise(s); e.g.
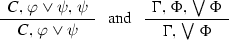
are instances of OR, respectively OR \(^+\).
- 5.
Of course, because of the presence of the rule W, the rule OR is a derived rule in \(\mathbf {T}_{\omega _1}\).
- 6.
The cut-elimination property of (the two-sided version of) \(\mathbf {T}^{\sharp }_{\omega _1}\) is exploited in [6] to prove cut-elimination for linear-time temporal logic \(\mathbf {LTL}\), by faithfully embedding \(\mathbf {LTL}\) into infinitary non-modal propositional logic.
- 7.
- 8.
The height of a derivation \(\mathfrak {D}\) in \(\mathbf {TK}_{\omega _1}\) is defined in the standard way: \(\mathtt {h}(\mathfrak {D})=0\) if \(\mathfrak {D}\) is an axiom (\(\mathtt {ID}\)), and \(\mathtt {h}(\mathfrak {D})=\sup \{\mathtt {h}(\mathfrak {D}_i)+1\mid i\in I\}\) if \(\mathfrak {D}\) results from derivations \(\{\mathfrak {D}_i\}_{i\in I}\) by an application of an |I|-premises inference rule \(\mathtt {W}\), \(\mathtt {OR}^+\), \(\mathtt {CUT}\) \((|I|\le 2)\), \(\mathtt {AND}\) \((|I|\le \omega )\). Of course \(\mathtt {h}(\mathfrak {D})\) can exceed finite ordinals due to the presence of the rule \(\mathtt {AND}\), possibly having denumerably many premises.
- 9.
Kripke-style semantics based on generalized Kripke frames not satisfying the condition (DD) have been considered in the literature (under diverse names, like multi-relational semantics, or multiplex semantics), see e.g. [2, 5, 13], in order to model various types of non-normal modal logics, in particular deontic systems allowing conflicts of obligation (in which case the relations \(R\in \mathfrak {R_i}\) are seen as distinct, possibly conflicting normative standards for agent i).
- 10.
In the usual Hilbert-style axiomatization of \(\mathbf {K}\) (classical tautologies, axiom-schema K and inference rules \(\mathtt {MP, RN}\)) one can equivalently replace K with the axiom schema \(\Box \varphi \wedge \Box \psi \rightarrow \Box (\varphi \wedge \psi )\) together with the inference rule \(\mathtt {RR}\). Multi-relational semantics in which the condition (DD) is not requested (see fn. 9) are thus typically used to model subsystems of \(\mathbf {K}\) in which \(\mathtt {RN}\) and \(\mathtt {RR}\) are accepted, while \(\Box \varphi \wedge \Box \psi \rightarrow \Box (\varphi \wedge \psi )\) is rejected.
References
K. Brünnler, Deep sequent systems for modal logic. Arch. Math. Logic 48, 551–577 (2009)
E. Calardo, A. Rotolo, Variants of multi-relational semantics for propositional non-normal modal logics. J. Appl. Non-Classical Logics 24, 293–320 (2014)
R. Fagin, J.Y. Halpern, Y. Moses, M.Y. Vardi, Reasoning About Knowledge (The MIT Press, Cambridge, 1995)
S. Feferman, Lectures on proof theory, in Proceedings of the Summer School in Logic, Leeds 1967, vol. 70, Lecture Notes in Mathematics, ed. by M.H. Löb (Springer, Berlin, 1967), pp. 1–107
L. Goble, Multiplex semantics for deontic logic. Nordic J. Philos. Logic 5, 113–134 (2000)
N. Kamide, Embedding linear-time temporal logic into infinitary logic: application to cut-elimination for multi-agent infinitary epistemic linear-time temporal logic, in Computational Logics in Multi-Agent Systems, vol. 5405, Lecture Notes in Artificial Intelligence, ed. by M. Fisher, F. Sadri, M. Thielscher (Springer, Berlin, 2009), pp. 57–76
E.G.K. Lopez-Escobar, An interpolation theorem for denumerably long formulas. Fundam. Math. 57, 253–272 (1965)
E.G.K. Lopez-Escobar, Remarks on an infinitary language with constructive formulas. J. Symb. Logic 32, 305–318 (1967)
P. Minari, Labeled sequent calculi for modal logics and implicit contractions. Arch. Math. Logic 52, 881–907 (2013)
S. Negri, Proof analysis in modal logic. J. Philos. Logic 34, 507–544 (2005)
M. Ohnishi, K. Matsumoto, Gentzen method in modal calculi. Osaka Math. J. 9, 113–130 (1957)
S. Radev, Infinitary propositional normal modal logic. Studia Logica 46, 291–309 (1987)
P. Schotch, R. Jennings, Non-kripkean deontic logic, in New Studies in Deontic Logic, ed. by R. Hilpinen (Reidel, Dordrecht, 1981), pp. 149–162
W.W. Tait, Normal derivability in classical logic, in The Syntax and Semantics of Infinitary Languages, vol. 72, Lecture Notes in Mathematics, ed. by J. Barwise (Springer, Berlin, 1968), pp. 204–236
Y. Tanaka, Kripke completeness of infinitary predicate multimodal logics. Notre Dame J. Formal Logic 40, 327–339 (1999)
Y. Tanaka, Cut-elimination theorems for some infinitary modal logics. Math. Logic Q. 47, 326–340 (2001)
Y. Tanaka, H. Ono, Rasiowa-Sikorski lemma and Kripke completeness of predicate and infinitary modal logics, in Advances in Modal Logic 98, vol. 2, ed. by M. Zakharyaschev, K. Segerberg, M. de Rijk, H. Wansing (CSLI Publications, Stanford, 2000), pp. 419–437
Acknowledgments
I wish to thank an anonymous referee for helpful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Minari, P. (2016). Some Remarks on the Proof-Theory and the Semantics of Infinitary Modal Logic. In: Kahle, R., Strahm, T., Studer, T. (eds) Advances in Proof Theory. Progress in Computer Science and Applied Logic, vol 28. Birkhäuser, Cham. https://doi.org/10.1007/978-3-319-29198-7_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-29198-7_8
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-319-29196-3
Online ISBN: 978-3-319-29198-7
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)