Abstract
We mainly prove that most d-dimensional convex surfaces \(\Sigma \) have a set of endpoints of Hausdorff dimension at least \(d-2\). A recent previous work of the author gave d / 3 as a lower bound, which is thus improved when \(d \ge 4\). Our proof uses a rather simple example where this dimension is \(d-2\) and the corresponding Hausdorff measure is positive. We also address several related problems. An endpoint is a point not lying in the interior of any shortest path in \(\Sigma \). “Most” means that the exceptions constitute a meager set, relatively to the usual Pompeiu-Hausdorff distance.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
One can also use as a more explicit denomination the term “Euclidean closed convex hypersurface”.
- 2.
- 3.
The set of outer unit normal vectors to \(\Sigma \) at points of \(U_\infty (C)\).
- 4.
- 5.
The idea of considering that kind of exemple came rather lately to my mind, after a conversation with David Guy.
- 6.
The tangent cone \(T_p(\Sigma )\) defined in the introduction is known to be isometric to the abstract tangent cone used in the framework of Alexandrov surfaces.
- 7.
We do not know a direct proof of Lemma 1, though it should exist for a so simple set.
- 8.
Indeed the unit ball of \(T_x\Sigma \) has smaller \(\mathcal {H}^d\)-measure than the unit ball of
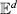 , the ratio being \(\displaystyle 2^{q-1} \sin ^{q-1} {\arctan r \over 2}\).
, the ratio being \(\displaystyle 2^{q-1} \sin ^{q-1} {\arctan r \over 2}\). - 9.
True for example in finite dimension.
- 10.
A proof of this is given in Lemma 4 of [15].
References
K. Adiprasito, Infinite curvature on typical convex surfaces. Geom. Dedicata 159, 267–275 (2012)
K. Adiprasito, T. Zamfirescu, Large curvature on typical convex surfaces. J. Convex Anal. 19(2), 385–391 (2012)
K. Adiprasito, T. Zamfirescu, Few Alexandrov surfaces are Riemann. J. Nonlinear Convex Anal. 16, 1147–1153 (2015)
A.D. Aleksandrov, Almost everywhere existence of the second differential of a convex function and some properties of convex surfaces connected with it. Uchen. Zap. Leningrad. Gos. Univ. Math. Ser. 6, 3–35 (1939). (in Russian)
Y. Burago, M. Gromov, G. Perel’man, A.D. Alexandrov spaces with curvature bounded below. Uspekhi mat. Naut, Russian Mah. Surveys 47(2), 1–58 (1992)
Y. Burago, D. Burago, S. Ivanov, A course in metric geometry. Amer. Math. Soc. (2001)
K. Falconer, Fractal Geometry (Wiley, 1990)
H. Federer, Geometric Measure Theory (Springer, Berlin, 1969)
V. Klee, Some new results on smoothness and rotundity in normed linear spaces. Math. Ann. 139, 51–63 (1959)
A.D. Milka, Geodesics and shortest lines on convex hypersurfaces. ii. smoothness of a hypersurface at points of a shortest line. (russian). Ukrain Geom. Sb., 26 103–110 (1983)
Y. Otsu, T. Shioya, The riemannian structure of Alexandrov spaces. J. Differ. Geom. 39(3), 629–658 (1994)
A. Petrunin, Parallel transportation for Alexandrov space with curvature bounded below. Geom. Funct. Anal. 1, 123–148 (1998)
A. Rivière, Dimension de Hausdorff de la nervure. Geom. Dedicata 85, 217–235 (2001)
A. Rivière, Hausdorff dimension of cut loci of generic subspaces of Euclidean spaces. J. Convex Anal. 14(4), 823–854 (2007)
A. Rivière, Hausdorff dimension and derivatives of typical nondecreasing continuous functions (2014).<hal-01154558>, https://hal.archives-ouvertes.fr/hal-01154558
A. Rivière, Hausdorff dimension of the set of endpoints of typical convex surfaces. J. Convex Anal. 22(2) (2015)
R. Schneider, Curvatures of typical convex bodies–the complete picture. Proc. Am. Math. Soc. 143, 387–393 (2015)
R. Schneider, Convex surfaces, curvature and surface area measures, in Handbook of Convex Geometry, vol. A, ed. by P. Gruber, J. Wills (Amsterdam Elserver Science, 1993), pp. 273–299
K. Shiohama, An introduction to the geometry of Alexandrov spaces. Lecture Notes Serie, 8. (Seoul National University, 1992)
C. Vîlcu, On typical degenerate convex surfaces. Math. Ann. 340(3), 543–567 (2008)
T. Zamfirescu, The curvature of most convex surfaces vanishes almost everywhere. Math. Z. 174, 135–139 (1980)
T. Zamfirescu, Nonexistence of curvature in most points of most convex surfaces. Math. Ann. 252, 217–219 (1980)
T. Zamfirescu, Many endpoints and few interior points of geodesics. Inventiones Mathematicae 69(1), 253–257 (1982)
T. Zamfirescu, On the cut locus in Alexandrov spaces and applications to convex surfaces. Pacific J. Math. 217(2), 375–386 (2004)
Acknowledgments
Thanks are due to Costin Vîlcu for many informations and useful suggestions, and to the referee, who greatly helped to improve the English and the presentation, and to eliminate some mistakes.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
Rivière, A. (2016). About the Hausdorff Dimension of the Set of Endpoints of Convex Surfaces. In: Adiprasito, K., Bárány, I., Vilcu, C. (eds) Convexity and Discrete Geometry Including Graph Theory. Springer Proceedings in Mathematics & Statistics, vol 148. Springer, Cham. https://doi.org/10.1007/978-3-319-28186-5_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-28186-5_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-28184-1
Online ISBN: 978-3-319-28186-5
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


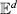 , the ratio being
, the ratio being