Simple Realizability of Complete Abstract Topological Graphs Simplified

Abstract

An abstract topological graph (briefly an AT-graph) is a pair $A=(G,\mathcal {X})$ where $G=(V,E)$ is a graph and $\mathcal {X}\subseteq \left( {\begin{array}{c}E\\ 2\end{array}}\right)$ is a set of pairs of its edges. The AT-graph A is simply realizable if G can be drawn in the plane so that each pair of edges from $\mathcal {X}$ crosses exactly once and no other pair crosses. We characterize simply realizable complete AT-graphs by a finite set of forbidden AT-subgraphs, each with at most six vertices. This implies a straightforward polynomial algorithm for testing simple realizability of complete AT-graphs, which simplifies a previous algorithm by the author.

J. Kynčl—Supported by Swiss National Science Foundation Grants 200021-137574 and 200020-14453, by the ESF Eurogiga project GraDR as GAČR GIG/11/E023, by the grant no. 14-14179S of the Czech Science Foundation (GAČR) and by the grant GAUK 1262213 of the Grant Agency of Charles University.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

A topological graph $T=(V(T), E(T))$ is a drawing of a graph G in the plane such that the vertices of G are represented by a set V(T) of distinct points and the edges of G are represented by a set E(T) of simple curves connecting the corresponding pairs of points. We call the elements of V(T) and E(T) the vertices and the edges of T, respectively. The drawing has to satisfy the following general position conditions: (1) the edges pass through no vertices except their endpoints, (2) every pair of edges has only a finite number of intersection points, (3) every intersection point of two edges is either a common endpoint or a proper crossing (“touching” of the edges is not allowed), and (4) no three edges pass through the same crossing. A topological graph or a drawing is simple if every pair of edges has at most one common point, which is either a common endpoint or a crossing. Simple topological graphs appear naturally as crossing-minimal drawings; it is well known that if two edges in a topological graph have more than one common point, then a local redrawing decreases the total number of crossings. A topological graph is complete if it is a drawing of a complete graph.

An abstract topological graph (briefly an AT-graph), a notion introduced by Kratochvíl, Lubiw and Nešetřil [10], is a pair $(G,\mathcal {X})$ where G is a graph and $\mathcal {X} \subseteq \left( {\begin{array}{c}E(G)\\ 2\end{array}}\right)$ is a set of pairs of its edges. Here we assume that $\mathcal {X}$ consists only of independent (that is, nonadjacent) pairs of edges. For a simple topological graph T that is a drawing of G, let $\mathcal {X}_T$ be the set of pairs of edges having a common crossing. A simple topological graph T is a simple realization of $(G,\mathcal {X})$ if $\mathcal {X}_T=\mathcal {X}$. We say that $(G,\mathcal {X})$ is simply realizable if $(G,\mathcal {X})$ has a simple realization.

An AT-subgraph of an AT-graph $(G,\mathcal {X})$ is an AT-graph $(H,\mathcal {Y})$ such that H is a subgraph of G and $\mathcal {Y}=\mathcal {X}\cap \left( {\begin{array}{c}E(H)\\ 2\end{array}}\right)$. Clearly, a simple realization of $(G,\mathcal {X})$ restricted to the vertices and edges of H is a simple realization of $(H,\mathcal {Y})$.

We are ready to state our main result.

Theorem 1

Every complete AT-graph that is not simply realizable has an AT-subgraph on at most six vertices that is not simply realizable.

We also show that AT-subgraphs with five vertices are not sufficient to characterize simple realizability.

Theorem 2

There is a complete AT-graph A with six vertices such that all its induced AT-subgraphs with five vertices are simply realizable, but A itself is not.

Theorem 1 implies a straightforward polynomial algorithm for simple realizability of complete AT-graphs, running in time $O(n^{6})$ for graphs with n vertices. It is likely that this running time can be improved relatively easily. However, compared to the first polynomial algorithm for simple realizability of complete AT-graphs [13], the new algorithm may be more suitable for implementation and for practical applications, such as generating all simply realizable complete AT-graphs of given size or computing the crossing number of the complete graph [5, 15]. On the other hand, the new algorithm does not directly provide the drawing itself, unlike the original algorithm [13]. The explicit list of realizable AT-graphs on six vertices can be generated using the database of small simple complete topological graphs created by Ábrego et al. [1].

For general noncomplete graphs, no such finite characterization by forbidden AT-subgraphs is possible. Indeed, in the special case when $\mathcal {X}$ is empty, the problem of simple realizability is equivalent to planarity, and there are nonplanar graphs of arbitrarily large girth, such as subdivisions of $K_5$. Moreover, simple realizability for general AT-graphs is NP-complete [11]. See [13] for an overview of other similar realizability problems.

The proof of Theorem 1 is based on the polynomial algorithm for simple realizability of complete AT-graphs from [13]. The main idea is very simple: every time the algorithm rejects the input, it is due to an obstruction of constant size.

Theorem 1 is an analogue of a similar characterization of simple monotone drawings of $K_n$ by forbidden 5-tuples, and pseudo linear drawings of $K_n$ by forbidden 4-tuples [4].

Ábrego et al. [1, 2] independently verified that simple complete topological graphs with up to nine vertices can be characterized by forbidden rotation systems of five-vertex subgraphs; see Sect. 2 for the definition. They conjectured that the same characterization is true for all simple complete topological graphs [2]. This conjecture now follows by combining their result for six-vertex graphs with Theorem 1. This gives a finite characterization of realizable abstract rotation systems defined in [14, Sect. 3.5], where it was also stated that such a characterization was not likely [14, p. 739]. The fact that only 5-tuples are sufficient for the characterization by rotation systems should perhaps not be too surprising, as rotation systems characterize simple drawings of $K_n$ more economically, using only $O(n^2\log n)$ bits, whereas AT-graphs need $\varTheta (n^4)$ bits.

2 Preliminaries

Topological graphs G and H are weakly isomorphic if they are realizations of the same abstract topological graph.

The rotation of a vertex v in a topological graph is the clockwise cyclic order in which the edges incident with v leave the vertex v. The rotation system of a topological graph is the set of rotations of all its vertices. Similarly we define the rotation of a crossing x of edges uv and yz as the clockwise order in which the four parts xu, xv, xy and xz of the edges uv and yz leave the point x. Note that each crossing has exactly two possible rotations. We will represent the rotation of a vertex v as an ordered sequence of the endpoints of the edges incident with v. The extended rotation system of a topological graph is the set of rotations of all its vertices and crossings.

Assuming that T and $T'$ are drawings of the same abstract graph, we say that their rotation systems are inverse if for each vertex $v \in V(T)$, the rotation of v and the rotation of the corresponding vertex $v' \in V(T')$ are inverse cyclic permutations. If T and $T'$ are weakly isomorphic simple topological graphs, we say that their extended rotation systems are inverse if their rotation systems are inverse and, in addition, for every crossing x in T, the rotation of x and the rotation of the corresponding crossing $x'$ in $T'$ are inverse cyclic permutations. For example, if $T'$ is a mirror image of T, then T and $T'$ have inverse extended rotation systems.

We say that two cyclic permutations of sets A, B are compatible if they are restrictions of a common cyclic permutation of $A\cup B$.

Simple complete topological graphs have the following key property.

Proposition 3

[7, 13].

• (1) If two simple complete topological graphs are weakly isomorphic, then their extended rotation systems are either the same or inverse.

• (2) For every edge e of a simple complete topological graph T and for every pair of edges $f,f'\in E(T)$ that have a common endpoint and cross e, the AT-graph of T determines the order of crossings of e with the edges $f,f'$.

By inspecting simple drawings of $K_4$, it can be shown that the converse of Proposition 3 also holds: the rotation system of a simple complete topological graph determines which pairs of edges cross [12, 16].

3 Proof of Theorem 2

We use the shortcut ij to denote the edge $\{i,j\}$. Let $A=((V,E),\mathcal {X})$ be the complete AT-graph with vertex set $V=\{0,1,2,3,4,5\}$ and with

$$\begin{aligned} \mathcal {X}=\{&\{02,13\},\{02,14\},\{02,15\},\{02,35\},\{03,14\},\{03,15\},\{03,24\},\\&\{04,15\},\{04,25\},\{04,35\},\{13,24\},\{24,35\},\{35,14\},\{14,25\},\{25,13\}\}. \end{aligned}$$

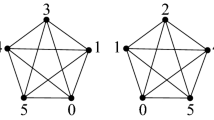
Every complete AT-subgraph of A with five vertices is simply realizable; see Fig. 1.

On the other hand, we show that A is not simply realizable. Suppose that T is a simple realization of A. Without loss of generality, assume that the rotation of 5 in $T[\{1,2,3,5\}]$ is (1, 2, 3). By Proposition 3 and by the first drawing in Fig. 1, the rotation of 5 in $T[\{1,2,3,4,5\}]$ is (1, 2, 3, 4), since the inverse would not be compatible with (1, 2, 3). Similarly, by the second drawing in Fig. 1 the rotation of 5 in $T[\{0,2,3,4,5\}]$ is (2, 3, 0, 4), since the inverse would not be compatible with (1, 2, 3, 4). By the third drawing in Fig. 1, the rotation of 5 in $T[\{0,1,3,4,5\}]$ is (0, 1, 3, 4) or (0, 4, 3, 1), but neither of them is compatible with both (1, 2, 3, 4) and (2, 3, 0, 4); a contradiction.

Fig. 1.

Simple realizations of all six complete subgraphs of A with five vertices.

4 Proof of Theorem 1

Let $A=(K_n,\mathcal {X})$ be a given complete abstract topological graph with vertex set $[n]=\{1,2,\dots ,n\}$. The algorithm from [13] for deciding simple realizability of A has the following three main steps: computing the rotation system, determining the homotopy class of every edge with respect to the edges incident with one chosen vertex v, and computing the number of crossings of every pair of edges in a crossing-optimal drawing with the rotation system and homotopy class fixed from the previous steps. We follow the algorithm and analyze each step in detail.

Step 1: Computing the Extended Rotation System

This step is based on the proof of Proposition 3; see [13, Proposition 3].

1(a) Realizability of 5-tuples. For every 5-tuple Q of vertices of A, the algorithm tests whether A[Q] is simply realizable. If not, then the 5-tuple certifies that A is not simply realizable. If A[Q] is simply realizable, then by Proposition 3, the algorithm computes a rotation system $\mathcal {R}(Q)$ such that the rotation system of every simple realization of A[Q] is either $\mathcal {R}(Q)$ or the inverse of $\mathcal {R}(Q)$.

1(b) Orienting 5-tuples. For every 5-tuple $Q\subseteq [n]$, the algorithm selects an orientation $\varPhi (\mathcal {R}(Q))$ of $\mathcal {R}(Q)$ so that for every pair of 5-tuples $Q,Q'$ having four common vertices and for each $x\in Q\cap Q'$, the rotations of x in $\varPhi (\mathcal {R}(Q))$ and $\varPhi (\mathcal {R}(Q'))$ are compatible. If there is no such orientation map $\varPhi$, the AT-graph A is not simply realizable. We show that in this case there is a set S of six vertices of A that certifies this.

Let $Q_1,Q_2$ be two 5-tuples with four common elements, let $\mathcal {R}_1$ be a rotation system on $Q_1$ and let $\mathcal {R}_2$ be a rotation system on $Q_2$. We say that $\mathcal {R}_1$ and $\mathcal {R}_2$ are compatible if for every $x\in Q_1\cap Q_2$, the rotations of x in $\mathcal {R}_1$ and $\mathcal {R}_2$ are compatible.

Let $\mathcal {G}$ be the graph with vertex set $\left( {\begin{array}{c}[n]\\ 5\end{array}}\right)$ and edge set consisting of those pairs $\{Q,Q'\}$ whose intersection has size 4. For every edge $\{Q,Q'\}$ of $\mathcal {G}$, at most one orientation of $\mathcal {R}(Q')$ is compatible with $\mathcal {R}(Q)$. If no orientation of $\mathcal {R}(Q')$ is compatible with $\mathcal {R}(Q)$, then the 6-tuple $S=Q\cup Q'$ certifies that A is not simply realizable. We may thus assume that for every edge $\{Q,Q'\}$ of $\mathcal {G}$, exactly one orientation of $\mathcal {R}(Q')$ is compatible with $\mathcal {R}(Q)$. Let $\mathcal {E}$ be the set of those edges $\{Q,Q'\}$ of $\mathcal {G}$ such that $\mathcal {R}(Q)$ and $\mathcal {R}(Q')$ are not compatible.

Call a set $\mathcal {W} \subseteq \left( {\begin{array}{c}[n]\\ 5\end{array}}\right)$ orientable if there is an orientation map $\varPhi$ assigning to every rotation system $\mathcal {R}(Q)$ with $Q\in \mathcal {W}$ either $\mathcal {R}(Q)$ itself or its inverse $(\mathcal {R}(Q))^{-1}$, such that for every pair of 5-tuples $Q,Q' \in \mathcal {W}$ with $|Q\cap Q'|=4$, the rotation systems $\varPhi (\mathcal {R}(Q))$ and $\varPhi (\mathcal {R}(Q'))$ are compatible.

Lemma 4

If $\left( {\begin{array}{c}[n]\\ 5\end{array}}\right)$ is not orientable, then there is a 6-tuple $S \subseteq [n]$ such that S 5 is not orientable.

Proof

Clearly, $\left( {\begin{array}{c}[n]\\ 5\end{array}}\right)$ is not orientable if and only if $\mathcal {G}$ has a cycle with an odd number of edges from $\mathcal {E}$. Call such a cycle a nonorientable cycle. We claim that if $\mathcal {G}$ has a nonorientable cycle, then $\mathcal {G}$ has a nonorientable triangle. Let $\mathcal {C}(\mathcal {G})$ be the cycle space of $\mathcal {G}$. The parity of the number of edges of $\mathcal {E}$ in $\mathcal {K}\in \mathcal {C}(\mathcal {G})$ is a linear form on $\mathcal {C}(\mathcal {G})$. Hence, to prove our claim, it is sufficient to show that $\mathcal {C}(\mathcal {G})$ is generated by triangles.

Suppose that $\mathcal {K}=F_1F_2\dots F_k$, with $k\ge 4$, is a shortest cycle in $\mathcal {G}$ that is not a sum of triangles in $\mathcal {C}(\mathcal {G})$. Then $\mathcal {K}$ is an induced cycle in $\mathcal {G}$, that is, $|F_i \cap F_j|\le 3$ if $2 \le |i-j| \le k-2$. Let $z\in F_1 \setminus F_2$. Then $z\in F_k$, otherwise $|F_k\cap F_1\cap F_2|=4$. Let i be the smallest index such that $i\ge 3$ and $z\in F_i$. We have $i\ge 4$, otherwise $|F_1\cap F_3|=|(F_1\cap F_2\cap F_3)\cup \{z\}|=4$. For every $j\in \{2,\dots ,i-2\}$, let $F'_j=(F_j\cap F_{j+1}) \cup \{z\}$. Then $\mathcal {K}$ is the sum of the closed walk $\mathcal {K}'=F_1F'_2\dots F'_{i-2}F_i \dots F_k$ and the triangles $F_1F_2F'_2,F_{i-1}F_iF'_{i-2}$, $F_jF_{j+1}F'_j$ for $j=2, \dots , i-2$ and $F_{j+1}F'_jF'_{j+1}$ for $j=2,\dots , i-3$; see Fig. 2. Since the length of $\mathcal {K}'$ is $k-1$, we have a contradiction with the choice of $\mathcal {K}'$.

Let $Q_1Q_2Q_3$ be a nonorientable triangle in $\mathcal {G}$. The 5-tuples $Q_1,Q_2,Q_3$ have either three or four common elements. Suppose that $|Q_1\cap Q_2\cap Q_3|=4$ and let $\{u,v,w,z\}=Q_1\cap Q_2\cap Q_3$. Then we may orient the rotation systems $\mathcal {R}(Q_1), \mathcal {R}(Q_2)$ and $\mathcal {R}(Q_3)$ so that the rotation of u in each of the orientations is compatible with (v, w, z). This implies that the rotations of u in the resulting rotation systems are pairwise compatible. Thus, the resulting rotation systems are pairwise compatible, a contradiction. Hence, we have $|Q_1\cap Q_2\cap Q_3|=3$, which implies that $|Q_1\cup Q_2\cup Q_3|=6$. Setting $S=Q_1\cup Q_2\cup Q_3$, the set $\left( {\begin{array}{c}S\\ 5\end{array}}\right)$ is not orientable.$\square$

Fig. 2.

Triangulating a cycle in $\mathcal {G}$. The vertices in the first row represent the vertices $F_1, \dots , F_i$ of the original cycle $\mathcal {K}$, the vertices in the second row represent the vertices $F'_2, \dots , F'_{i-2}$.

If $\left( {\begin{array}{c}[n]\\ 5\end{array}}\right)$ is orientable, there are exactly two possible solutions for the orientation map. We will assume that the rotation of 1 in $\varPhi (\mathcal {R}(\{1,2,3,4,5\}))$ is compatible with (2, 3, 4), so that there is at most one solution $\varPhi$.

1(c) Computing the Rotations of Vertices. Having oriented the rotation system of every 5-tuple, the algorithm now computes the rotation of every $x\in [n]$, as the cyclic permutation compatible with the rotation of x in every $\varPhi (\mathcal {R}(Q))$ such that $x\in Q \in \left( {\begin{array}{c}[n]\\ 5\end{array}}\right)$. We show that this is always possible. The following lemma forms the core of the argument.

Lemma 5

Let $k\ge 4$. For every $F\in \left( {\begin{array}{c}[k+1]\\ k\end{array}}\right)$, let $\pi _F$ be a cyclic permutation of F such that for every pair $F,F'\in \left( {\begin{array}{c}[k+1]\\ k\end{array}}\right)$, the cyclic permutations $\pi _F$ and $\pi _F'$ are compatible. Then there is a cyclic permutation $\pi _{[k+1]}$ of $[k+1]$ compatible with all the cyclic permutations $\pi _F$ with $F\in \left( {\begin{array}{c}[k+1]\\ k\end{array}}\right)$.

1(d) Computing the Rotations of Crossings. For every pair of edges $\{\{u,v\},\{x,y\}\}\in \mathcal {X}$, the algorithm determines the rotation of their crossing from the rotations of the vertices u, v, x, y. This finishes the computation of the extended rotation system.

Step 2: Determining the Homotopy Classes of the Edges

Let v be a fixed vertex of A and let S(v) be a topological star consisting of v and all the edges incident with v, drawn in the plane so that the rotation of v agrees with the rotation computed in the previous step. For every edge $e=xy$ of A not incident with v, the algorithm computes the order of crossings of e with the subset $E_{v,e}$ of edges of S(v) that e has to cross. By Proposition 3 (2), the five-vertex AT-subgraphs of A determine the relative order of crossings of e with every pair of edges of $E_{v,e}$. Define a binary relation $\prec _{x,y}$ on $E_{v,e}$ so that $vu \prec _{x,y} vw$ if the crossing of e with vu is closer to x than the crossing of e with vw. If $\prec _{x,y}$ is acyclic, it defines a total order of crossings of e with the edges of $E_{v,e}$. If $\prec _{x,y}$ has a cycle, then it also has an oriented triangle $vu_1,vu_2,vu_3$. This means that the AT-subgraph of A induced by the six vertices $v,u_1,u_2,u_3,x,y$ is not simply realizable.

We recall that the homotopy class of a curve $\varphi$ in a surface $\varSigma$ relative to the boundary of $\varSigma$ is the set of all curves that can be obtained from $\varphi$ by a continuous deformation within $\varSigma$, keeping the boundary of $\varSigma$ fixed.

The homotopy class of e is determined by the following combinatorial data: the set $E_{v,e}$, the total order $\prec _{x,y}$ in which the edges of $E_{v,e}$ cross e, the rotations of these crossings, and the rotations of the vertices x and y. Consider the star S(v) drawn on the sphere. Cut circular holes around the points representing all the vertices except v, and let $\varSigma$ be the resulting surface with boundary. Let $x_e$ and $y_e$ be fixed points on the boundaries of the two holes around x and y, respectively, so that the orders of these points corresponding to all the edges of A on the boundaries of the holes agree with the computed rotation system. Draw a curve $\varphi _e$ with endpoints $x_e$ and $y_e$ satisfying all the combinatorial data of e. Now the homotopy class of e is defined as the homotopy class of $\varphi _e$ in $\varSigma$ relative to the boundary of $\varSigma$.

Step 3: Computing the Minimum Crossing Numbers

For every pair of edges e, f, let $\mathrm{cr}(e,f)$ be the minimum possible number of crossings of two curves from the homotopy classes of e and f. Similarly, let $\mathrm{cr}(e)$ be the minimum possible number of self-crossings of a curve from the homotopy class of e. The numbers $\mathrm{cr}(e,f)$ and $\mathrm{cr}(e)$ can be computed in polynomial time in any 2-dimensional surface with boundary [3, 17]. In our special case, the algorithm is relatively straightforward [13].

We use the key fact that from the homotopy class of every edge, it is possible to choose a representative such that the crossing numbers $\mathrm{cr}(e,f)$ and $\mathrm{cr}(e)$ are all realized simultaneously [13]. This is a consequence of the following facts.

Lemma 6

[9]. Let $\gamma$ be a curve on an orientable surface S with endpoints on the boundary of S that has more self-intersections than required by its homotopy class. Then there is a singular 1-gon or a singular 2-gon bounded by parts of $\gamma$.

Here a singular 1-gon of a curve $\gamma :[0,1] \rightarrow S$ is an image $\gamma [\alpha ]$ of an interval $\alpha \subset [0,1]$ such that $\gamma$ identifies the endpoints of $\alpha$ and the resulting loop is contractible in S. A singular 2-gon of $\gamma$ is an image of two disjoint intervals $\alpha , \beta \subset [0,1]$ such that $\gamma$ identifies the endpoints of $\alpha$ with the endpoints of $\beta$ and the resulting loop is contractible in S.

Lemma 7

[6, 9]. Let $C_1$ and $C_2$ be two simple curves on a surface S such that the endpoints of $C_1$ and $C_2$ lie on the boundary of S. If $C_1$ and $C_2$ have more intersections than required by their homotopy classes, then there is an innermost embedded 2-gon between $C_1$ and $C_2$, that is, two subarcs of $C_1$ and $C_2$ bounding a disc in S whose interior is disjoint with $C_1$ and $C_2$.

Whenever there is a singular 1-gon, a singular 2-gon, or an embedded innermost 2-gon in a system of curves on S, it is possible to eliminate the 1-gon or 2-gon by a homotopy of the corresponding curves, which decreases the total number of crossings.

For the rest of the proof, we fix a drawing D of A such that its rotation system is the same as the rotation system computed in Step 1, the edges of S(v) do not cross each other, every other edge is drawn as a curve in its homotopy class computed in Step 2, and under these conditions, the total number of crossings is the minimum possible. Then every edge f of S(v) crosses every other edge e at most once, and this happens exactly if $\{e,f\}\in \mathcal {X}$. Moreover, for every pair of edges $e_1, e_2$ not incident with v, the corresponding curves in D cross exactly $\mathrm{cr}(e_1,e_2)$ times, and the curve representing $e_1$ has $\mathrm{cr}(e_1)$ self-crossings. Hence, A is simply realizable if and only if all the edges $e_1,e_2$ not incident with v satisfy $\mathrm{cr}(e_1)=0$, $\mathrm{cr}(e_1,e_2)\le 1$, and $\mathrm{cr}(e_1,e_2)=1 \Leftrightarrow \{e_1,e_2\}\in \mathcal {X}$. Moreover, if A is simply realizable, then D is a simple realization of A.

We further proceed in four substeps. Due to space limitations, we only include a short sketch of the substeps 3(b)–3(d).

3(a) Characterization of the Homotopy Classes. Let $w_1, w_2, \dots , w_{n-1}$ be the vertices of A adjacent to v so that the rotation of v is $(w_1,w_2, \dots , w_{n-1})$. Let $w_aw_b$ be an edge such that $1\le a<b\le n-1$. Since every AT-subgraph of A with 4 or 5 vertices is simply realizable, we have the following conditions on the homotopy class of $w_aw_b$. Refer to Fig. 3.

Observation 8

Suppose that $\{w_aw_b,vw_c\}\in \mathcal {X}$; that is, $vw_c\in E_{v,w_aw_b}$. If $a<c<b$, then the rotation of the crossing of $w_aw_b$ with $vw_c$ is $(w_a,w_c,w_b,v)$. If $c<a$ or $b<c$, then the rotation of the crossing is $(w_b,w_c,w_a,v)$. $\square$

Fig. 3.

A drawing of a “typical” edge $w_aw_b$ and the star S(v).

Observation 8 implies that the homotopy class of the edge $w_aw_b$ is determined by a permutation of $E_{v,w_aw_b}$ that determines the order in which $w_aw_b$ crosses the edges in $E_{v,w_aw_b}$. The next observation further restricts this permutation.

Observation 9

Suppose that $vw_c,vw_d\in E_{v,w_aw_b}$. If $a<c<d<b$, then $vw_c \prec _{w_a,w_b} vw_d$. If (c, d, a, b) is compatible with $(1,2,\dots ,n-1)$ as cyclic permutations, then $vw_d \prec _{w_a,w_b} vw_c$. $\square$

On the other hand, it is easy to see that every homotopy class satisfying Observations 8 and 9 has a representative that is a simple curve. Therefore, $cr(w_aw_b)=0$.

3(b) The Parity of the Crossing Numbers. It can be shown that if $e_1$ and $e_2$ are independent edges not incident with v, then $\mathrm{cr}(e_1,e_2)$ is odd if and only if $\{e_1,e_2\}\in \mathcal {X}$. It can also be shown that if $e_1$ and $e_2$ are adjacent edges not incident with v, then $\mathrm{cr}(e_1,e_2)$ is even. It follows that A is realizable if and only if every pair of edges in D crosses at most once.

3(c) Multiple Crossings of Adjacent Edges. Next we show that adjacent edges do not cross in D, otherwise some AT-subgraph of A with five vertices is not simply realizable. This part is rather straightforward, although the full proof is not short. Let $w_aw_b$ and $w_aw_c$ be two adjacent edges. By symmetry, we may assume that $a<b<c$. We will consider cyclic intervals (a, b), (b, c) and $(c,a)=(c,n-1] \cup [1,a)$. We define the following subsets of $E_{v,w_aw_b}$ and $E_{v,w_aw_c}$. For each of the three cyclic intervals (i, j), let $F_b(i,j)=\{vw_k\in E_{v,w_aw_b}; k\in (i,j)\}$ and $F_c(i,j)=\{vw_k\in E_{v,w_aw_c}; k\in (i,j)\}$. We will also write $\prec _b$ as a shortcut for $\prec _{w_aw_b}$ and $\prec _c$ as a shortcut for $\prec _{w_aw_c}$. By symmetry, we have two general cases: (I) $w_aw_b$ does not cross $vw_c$ and $w_aw_c$ does not cross $vw_b$, and (II) $w_aw_b$ does not cross $vw_c$ and $w_aw_c$ crosses $vw_b$.

For case (I), one can observe the following conditions; we omit the proofs.

Observation 10

.

• (1) We have $F_b(c,a) \subseteq F_c(c,a)$ and $F_c(a,b) \subseteq F_b(a,b)$.

• (2) The sets $F_b(b,c)$ and $F_c(b,c)$ are disjoint.

• (3) If $vw_d\in F_b(b,c)$ and $vw_e\in F_c(b,c)$, then $d<e$.

• (4) Let $vw_d\in F_b(a,b)\cap F_c(a,b)$ and $vw_e\in F_b(c,a)\cap F_c(c,a)$. Then $vw_d \prec _b vw_e \Leftrightarrow vw_d \prec _c vw_e$.

• (5) Let $vw_d\in F_c(a,b)$ and $vw_e\in F_b(b,c)$. Then $vw_d \prec _b vw_e$. Similarly, if $vw_d\in F_b(c,a)$ and $vw_e\in F_c(b,c)$, then $vw_d \prec _c vw_e$.

Fig. 4.

A drawing of the edges $w_aw_b$, $w_aw_c$ and parts of edges of S(v) in case (I), where $w_aw_b$ and $w_aw_c$ do not cross. The rotation of v is compatible with the counterclockwise cyclic order of the parts of the edges drawn.

We show that Observation 10 implies that $\mathrm{cr}(w_aw_b, w_aw_c)=0$. Refer to Fig. 4. Start with drawing the edges $w_aw_b$ and $w_aw_c$ without crossing. Conditions (2) and (4) imply that there is a total order $\prec$ on $E_{v,w_aw_b} \cup E_{v,w_aw_c}$ that is a common extension of $\prec _b$ and $\prec _c$. Let $vw_i$ be the $\prec$-largest element of $F_b(c,a) \cup F_c(a,b)$. Condition (5) implies that all edges $vw_j$ from $F_b(b,c) \cup F_c(b,c)$ satisfy $vw_i \prec vw_j$. Condition (1) implies that we can draw the edges $vw_j$ with $vw_j \preceq vw_i$ like in the figure. Conditions (2), (3) and (5) imply that we can draw the edges $vw_j$ with $vw_i \prec vw_j$ like in the figure. The remaining edges of S(v) can be drawn easily. In this way we obtain a simple drawing with noncrossing representatives of the homotopy classes of $w_aw_b$ and $w_aw_c$.

The analysis of case (II) is similar.

3(d) Detecting Multiple Crossings of Independent Edges. Finally, we show by induction that if two independent edges cross more than once, then there is a five-vertex AT-subgraph that forces this, possibly for a different pair of edges. In this part, we strongly rely on the established fact that adjacent edges do not cross in D. We avoid a tedious case analysis by not continuing in the approach chosen for adjacent pairs of edges.

Let $e=w_aw_b$ and $f=w_cw_d$ be two independent edges that cross more than once in D. In the subgraph of D formed by the two edges e and f, the vertices $w_a,w_b,w_c,w_d$ are incident to a common face, since adjacent edges do not cross in D and every pair of the four vertices $w_a,w_b,w_c,w_d$ is connected by an edge. We assume without loss of generality that $w_a,w_b,w_c,w_d$ are incident to the outer face. That is, we may draw a simple closed curve $\gamma$ containing the vertices $w_a,w_b,w_c,w_d$ but no interior points of e or f, such that the relative interiors of e and f are inside $\gamma$.

Suppose that e and f cross an even number of times. The edge e splits the region inside $\gamma$ into two regions, $R_0(e)$ and $R_1(e)$, where $R_0(e)$ is the region that does not contain the endpoints of f on its boundary. Similarly, f splits the region inside $\gamma$ into regions $R_0(f)$ and $R_1(f)$ where $R_0(f)$ is the region that does not contain the endpoints of e on its boundary.

Fig. 5.

Four types of bigons between e and f. An ij-bigon is denoted by $B_{ij}$.

By Lemma 7, there is an innermost embedded 2-gon between e and f. For brevity, we call an innermost embedded 2-gon shortly a bigon. For a bigon B, by $B^o$ we denote the open region inside B and we call it the inside of B. There are four possible types of bigons between e and f, according to the regions $R_i(e)$ and $R_j(f)$ in which their insides are contained. For $i,j\in \{0,1\}$, we call a bigon B an ij-bigon if $B^o\subseteq R_i(e) \cap R_j(f)$; see Fig. 5.

Since D is a drawing realizing the crossing number $\mathrm{cr}(e,f)$, there is at least one vertex of D inside every bigon. The graph induced by v, the endpoints of e and f, and a set of vertices intersecting all bigons, certifies that e and f have at least $\mathrm{cr}(e,f)$ crossings forced by their homotopy classes.

The following lemma quickly solves the case when there is at least one 00-bigon between e and f.

Lemma 11

If e and f cross evenly and there is a 00-bigon B between e and f in D, then there is a vertex $w_i$ inside B, and the AT-subgraph of A induced by the 5-tuple $Q=\{w_a,w_b,w_c,w_d,w_i\}$ is not simply realizable.

We are left with the case that there is no 00-bigon between e and f.

Observation 12

If e and f cross evenly and at least twice in D, and there is no 00-bigon between e and f, then there is a 01-bigon and a 10-bigon between e and f.

For a subset W of vertices of A containing v and the endpoints of two edges g and f, let $\mathrm{cr}_W(g,f)$ be the minimum possible number of crossings of two curves from the homotopy classes of g and f determined by A[W], by a procedure analogous to the one in Step 2.

The following lemma proves the induction step in the case when e and f cross an even number of times.

Lemma 13

If e and f cross evenly and at least twice in D, and there is no 00-bigon between e and f, then there is a proper subset W of vertices of A and an edge g independent from f such that $\mathrm{cr}_W(g,f) \ge 2$.

If e and f cross an odd number of times, one can easily find another pair of independent edges crossing evenly and more than once. We omit the details.