Skip to main content
SpringerLink
Log in
Book cover

International Joint Conference on Computational Intelligence

IJCCI 2014: Computational Intelligence pp 213–234Cite as

Unsatisfiable Formulae of Gödel Logic with Truth Constants and \(\varDelta \) Are Recursively Enumerable

  • Conference paper
  • First Online:

  • 498 Accesses

Part of the book series: Studies in Computational Intelligence ((SCI,volume 620))

Abstract

This paper brings a solution to the open problem of recursive enumerability of unsatisfiable formulae in the first-order Gödel logic. The answer is affirmative even for a useful expansion by intermediate truth constants and the projection operator . The affirmative result for unsatisfiable prenex formulae of \(G_\infty ^\varDelta \) has been stated in [1]. In [2], we have generalised the well-known hyperresolution principle to the first-order Gödel logic for the general case. We now propose a modification of the hyperresolution calculus suitable for automated deduction with explicit partial truth.

This work is partially supported by VEGA Grant 1/0592/14.

This is a preview of subscription content, log in via an institution.

Chapter
USD   29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD   129.00
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD   169.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info
Hardcover Book
USD   169.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Learn about institutional subscriptions

Notes

  1. 1.

    Cf. http://ii.fmph.uniba.sk/~guller/sci15.pdf, Sect. 2.

  2. 2.

    We assume a decreasing connective and quantifier precedence: \(\forall \), \(\exists \), \(\lnot \), 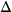, \(\wedge \), \(\rightarrow \), , , \(\vee \).

  3. 3.

    We assume a decreasing operator precedence: , , , , , , .

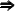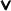  4. 4.

    Cf. http://ii.fmph.uniba.sk/~guller/sci15.pdf, Appendix, Sect. 5.1.

References

  1. Baaz, M., Ciabattoni, A., Fermüller, C.G.: Theorem proving for prenex Gödel logic with Delta: checking validity and unsatisfiability. Log. Methods Comput. Sci. 8 (2012)

    Google Scholar 

  2. Guller, D.: An order hyperresolution calculus for Gödel logic—General first-order case. In: Rosa, A.C., Correia, A.D., Madani, K., Filipe, J., Kacprzyk, J. (eds.) IJCCI 2012—Proceedings of the 4th International Joint Conference on Computational Intelligence, Barcelona, Spain, 5–7 October 2012, pp. 329–342. SciTePress (2012)

    Google Scholar 

  3. Davis, M., Putnam, H.: A computing procedure for quantification theory. J. ACM 7, 201–215 (1960)

    Article  MathSciNet  Google Scholar 

  4. Davis, M., Logemann, G., Loveland, D.: A machine program for theorem-proving. Commun. ACM 5, 394–397 (1962)

    Article  MathSciNet  Google Scholar 

  5. Robinson, J.A.: A machine-oriented logic based on the resolution principle. J. ACM 12, 23–41 (1965)

    Article  MathSciNet  Google Scholar 

  6. Robinson, J.A.: Automatic deduction with hyper-resolution. Int. J. Comput. Math. 1, 227–234 (1965)

    MathSciNet  Google Scholar 

  7. Gallier, J.H.: Logic for Computer Science: Foundations of Automatic Theorem Proving. Harper and Row Publishers Inc, New York (1985)

    Google Scholar 

  8. Biere, A., Heule, M.J., van Maaren, H., Walsh, T.: Handbook of Satisfiability. Frontiers in Artificial Intelligence and Applications, vol. 185. IOS Press, Amsterdam (2009)

    Google Scholar 

  9. Hájek, P.: Metamathematics of Fuzzy Logic. Trends in Logic. Springer (2001)

    Google Scholar 

  10. Pavelka, J.: On fuzzy logic I, II, III. Semantical completeness of some many-valued propositional calculi. Math. Logic Q. 25, 45–52, 119–134, 447–464 (1979)

    Google Scholar 

  11. Novák, V., Perfilieva, I., Močkoř, J.: Mathematical Principles of Fuzzy Logic. The Springer International Series in Engineering and Computer Science. Springer, US (1999)

    Book  Google Scholar 

  12. Esteva, F., Godo, L., Montagna, F.: The Ł\(\rm {\Pi }\) and Ł\(\rm {\Pi }\) \(\frac{1}{2}\) logics: two complete fuzzy systems joining Łukasiewicz and product logics. Arch. Math. Log. 40, 39–67 (2001)

    Google Scholar 

  13. Savický, P., Cignoli, R., Esteva, F., Godo, L., Noguera, C.: On product logic with truth-constants. J. Log. Comput. 16, 205–225 (2006)

    Article  MathSciNet  Google Scholar 

  14. Esteva, F., Godo, L., Noguera, C.: On completeness results for the expansions with truth-constants of some predicate fuzzy logics. In: Stepnicka, M., Novák, V., Bodenhofer, U. (eds.) New Dimensions in Fuzzy Logic and Related Technologies. Proceedings of the 5th EUSFLAT Conference, Ostrava, Czech Republic, September 11–14, 2007, Volume 2: Regular Sessions, Universitas Ostraviensis, pp. 21–26 (2007)

    Google Scholar 

  15. Esteva, F., Gispert, J., Godo, L., Noguera, C.: Adding truth-constants to logics of continuous t-norms: axiomatization and completeness results. Fuzzy Sets Syst. 158, 597–618 (2007)

    Article  MathSciNet  Google Scholar 

  16. Esteva, F., Godo, L., Noguera, C.: First-order t-norm based fuzzy logics with truth-constants: distinguished semantics and completeness properties. Ann. Pure Appl. Logic 161, 185–202 (2009)

    Article  MathSciNet  Google Scholar 

  17. Esteva, F., Godo, L., Noguera, C.: Expanding the propositional logic of a t-norm with truth-constants: completeness results for rational semantics. Soft Comput. 14, 273–284 (2010)

    Article  Google Scholar 

  18. Esteva, F., Godo, L., Noguera, C.: On expansions of WNM t-norm based logics with truth-constants. Fuzzy Sets Syst. 161, 347–368 (2010)

    Article  MathSciNet  Google Scholar 

  19. Guller, D.: A generalisation of the hyperresolution principle to first order Gödel logic. In: Computational Intelligence—International Joint Conference, IJCCI 2012 Barcelona, Spain, October 5–7, 2012 Revised Selected Papers. Studies in Computational Intelligence, vol. 577, pp. 159–182. Springer (2015)

    Google Scholar 

  20. Guller, D.: An order hyperresolution calculus for Gödel logic with truth constants. In: Rosa, A.C., Dourado, A., Correia, K.M., Filipe, J., Kacprzyk, J. (eds.) FCTA 2014—Proceedings of the 6th International Joint Conference on Computational Intelligence, Rome, Italy, 22–24 October 2014, pp. 37–52. SciTePress (2014)

    Google Scholar 

  21. Apt, K.R.: Introduction to logic programming. Technical Report CS-R8826, Centre for Mathematics and Computer Science, Amsterdam, The Netherlands (1988)

    Google Scholar 

  22. Guller, D.: On the refutational completeness of signed binary resolution and hyperresolution. Fuzzy Sets Syst. 160, 1162–1176 (2009). Featured Issue: Formal Methods for Fuzzy Mathematics. Approximation and Reasoning, Part II

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Applied Informatics, Comenius University, Mlynská Dolina, 842 48, Bratislava, Slovakia

    Dušan Guller

Authors
  1. Dušan Guller
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dušan Guller .

Editor information

Editors and Affiliations

  1. Ingenería Informática, Escuela Técnica Superior de, Granada, Spain

    Juan Julian Merelo

  2. aSEEB-ISR-IST, Technical University of Lisbon (IST), Lisbon, Portugal

    Agostinho Rosa

  3. Facultad de Informática, University of Murcia, Murcia, Spain

    José M. Cadenas

  4. University of Coimbra, Coimbra, Portugal

    António Dourado

  5. Images, Signals and Intelligence, University PARIS-EST Créteil (UPEC), Créteil, France

    Kurosh Madani

  6. Instituto Politécnico de Setúbal (IPS), Setúbal, Portugal

    Joaquim Filipe

Rights and permissions

Reprints and permissions

Copyright information

© 2016 Springer International Publishing Switzerland

About this paper

Cite this paper

Guller, D. (2016). Unsatisfiable Formulae of Gödel Logic with Truth Constants and \(\varDelta \) Are Recursively Enumerable. In: Merelo, J.J., Rosa, A., Cadenas, J.M., Dourado, A., Madani, K., Filipe, J. (eds) Computational Intelligence. IJCCI 2014. Studies in Computational Intelligence, vol 620. Springer, Cham. https://doi.org/10.1007/978-3-319-26393-9_13

Download citation

  • DOI: https://doi.org/10.1007/978-3-319-26393-9_13

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-319-26391-5

  • Online ISBN: 978-3-319-26393-9

  • eBook Packages: EngineeringEngineering (R0)

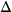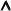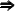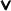Publish with us

Policies and ethics

Search

Navigation