Abstract
We present Balloon, a forward-secure append-only persistent authenticated data structure. Balloon is designed for an initially trusted author that generates events to be stored in a data structure (the Balloon) kept by an untrusted server, and clients that query this server for events intended for them based on keys and snapshots. The data structure is persistent such that clients can query keys for the current or past versions of the data structure based upon snapshots, which are generated by the author as new events are inserted. The data structure is authenticated in the sense that the server can verifiably prove all operations with respect to snapshots created by the author. No event inserted into the data structure prior to the compromise of the author can be modified or deleted without detection due to Balloon being publicly verifiable. Balloon supports efficient (non-)membership proofs and verifiable inserts by the author, enabling the author to verify the correctness of inserts without having to store a copy of the Balloon. We formally define and prove that Balloon is a secure authenticated data structure.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
This paper is motivated by the lack of an appropriate data structure that would enable the trust assumptions to be relaxed for privacy-preserving transparency logging. In the setting of transparency logging, an author logs messages intended for clients through a server: the author sends messages to the server, and clients poll the server for messages intended for it. Previous work [21] assumes a forward security model: both the author and the server are assumed to be initially trusted and may be compromised at some point in time. Any messages logged before this compromise remain secure and private. One can reduce the trust assumptions at the server by introducing a secure hardware extension at the server as in [25].
This paper proposes a novel append-only authenticated data structure that allows the server to be untrusted without the need for trusted hardware. Our data structure, which is named Balloon, allows for efficient proofs of both membership and non-membership. As such, the server is forced to provide a verifiable reply to all queries. Balloon also provides efficient (non-)membership proofs for past versions of the data structure (making it persistent), which is a key property for providing proofs of time, when only some versions of the Balloon have been time-stamped. Since Balloon is append-only, we can greatly improve the efficiency in comparison with other authenticated data structures that provide the same properties as described above, such as persistent authenticated dictionaries [1].
Balloon is a key building block for privacy-preserving transparency logging to make data processing by service providers transparent to data subjects whose personal data are being processed. Balloon can also be used as part of a secure logging system, similar to the history tree system by Crosby and Wallach [6]. Another closely related application is as an extension to Certificate Transparency (CT) [12], where Balloon can be used to provide efficient non-membership proofs, which are highly relevant in relation to certificate revocation for CT [11, 12, 18].
For formally defining and proving the security of Balloon, we take a similar approach as Papamanthou et al. [19]. We view Balloon in the model of authenticated data structures (ADS), using the three-party setting [24]. The three party setting for ADS consists of the source (corresponding to our author), one or more servers, and one or more clients. The source is a trusted party that authors a data structure (the Balloon) that is copied to the untrusted servers together with some additional data that authenticates the data structure. The servers answer queries made by clients. The goal for an ADS is for clients to be able to verify the correctness of replies to queries based only on public information. The public information takes the form of a verification key, for verifying signatures made by the source, and some digest produced by the source to authenticate the data structure. The source can update the ADS, in the process producing new digests, to which is further referred to as snapshots. The reply we want to enable clients to verify is the outcome of a membership query, which proves membership or non-membership of an event with a provided key for a provided snapshot.
After we show that Balloon is a secure ADS in the three party setting, we extend Balloon to enable the author to discard the data structure and still perform verifiable inserts of new events to update the Balloon. Finally, we describe how monitors and a perfect gossiping mechanism would prevent the an author from undetectably modifying or deleting events once inserted into the Balloon, which lays the foundation for the forward-secure author setting.
We make the following contributions:
-
A novel append-only authenticated data structure named Balloon that allows for both efficient membership and non-membership proofs, also for past versions of the Balloon, while keeping the storage and memory requirements minimal (Sect. 3).
-
We formally prove that Balloon is a secure authenticated data structure (Sect. 4) according to the definition by Papamanthou et al. [19].
-
Efficient verifiable inserts into our append-only authenticated data structure that enable the author to ensure consistency of the data structure without storing a copy of the entire (authenticated) data structure (Sect. 5).
-
We define publicly verifiable consistency for an ADS scheme and show how it enables a forward-secure source (Sect. 6). Verifiable inserts can also have applications for monitors in, e.g., [3, 10–12, 22, 27].
-
In Sect. 7, we show that Balloon is practical, providing performance results for a proof-of-concept implementation.
The rest of the paper is structured as follows. Section 2 introduces the background of our idea. Section 8 presents related work and compares Balloon to prior work. Section 9 concludes the paper. Of independent interest, Appendix B shows why probabilistic proofs are insufficient for ensuring consistency of a Balloon without the burden on the prover increasing greatly.
2 Preliminaries
First, we introduce the used formalisation of an authenticated data structure scheme. Next, we give some background on the two data structures that make up Balloon: a history tree, for efficient membership proofs for any snapshot, and a hash treap, for efficient non-membership proofs. Finally we present our cryptographic building blocks.
2.1 An Authenticated Data Structure Scheme
Papamanthou et al. [19] define an authenticated data structure and its two main properties: correctness and security. We make use of these definitions and therefore present them here, be it with slight modifications to fit our terminology.
Definition 1
(ADS scheme). Let D be any data structure that supports queries q and updates u. Let auth(D) denote the resulting authenticated data structure and \(\mathsf{s}\) the snapshot of the authenticated data structure, i.e., a constant-size description of D. An ADS scheme \(\mathcal {A}\) is a collection of the following six probabilistic polynomial-time algorithms:
-
1.
{\(\mathtt{sk}, \mathtt{pk}\)} \({\leftarrow }\) genkey(\(1^\lambda \)): On input of the security parameter \(\lambda \), it outputs a secret key \(\mathtt{sk}\) and public key \(\mathtt{pk}\);
-
2.
\(\{{{\texttt {\textit{auth}}}}(D_{0}),\mathsf{s}_0\} \, {\leftarrow }\, {{\texttt {\textit{setup}}}}(D_0,\mathtt{sk},\mathtt{pk})\): On input of a (plain) data structure \(D_0\), the secret key \(\mathtt{sk}\), and the public key \(\mathtt{pk}\), it computes the authenticated data structure \({{\texttt {\textit{auth}}}}(D_{0})\) and the corresponding snapshot \(\mathsf{s}_0\);
-
3.
\(\{D_{h+1}, {{\texttt {\textit{auth}}}}(D_{h+1}), \mathsf{s}_{h+1}, upd\} \; {\leftarrow }\; {{\texttt {\textit{update}}}}(u, D_h, {{\texttt {\textit{auth}}}}(D_{h}), \mathsf{s}_h, \mathtt{sk}, \mathtt{pk})\): On input of an update u on the data structure \(D_h\), the authenticated data structure \({{\texttt {\textit{auth}}}}(D_{h})\), the snapshot \(\mathsf{s}_h\), the secret key \(\mathtt{sk}\), and the public key \(\mathtt{pk}\), it outputs the updated data structure \(D_{h+1}\) along with the updated authenticated data structure \({{\texttt {\textit{auth}}}}(D_{h+1})\), the updated snapshot \(\mathsf{s}_{h+1}\) and some relative information upd;
-
4.
\(\{D_{h+1}, {{\texttt {\textit{auth}}}}(D_{h+1}), \mathsf{s}_{h+1}\} \; {\leftarrow }\; {{\texttt {\textit{refresh}}}}(u, D_h, {{\texttt {\textit{auth}}}}(D_{h}), \mathsf{s}_h, upd, \mathtt{pk})\): On input of an update u on the data structure \(D_h\), the authenticated data structure \({{\texttt {\textit{auth}}}}(D_{h})\), the snapshot \(\mathsf{s}_h\), relative information upd and the public key \(\mathtt{pk}\), it outputs the updated data structure \(D_{h+1}\) along with the updated authenticated data structure \({{\texttt {\textit{auth}}}}(D_{h+1})\) and the updated snapshot \(\mathsf{s}_{h+1}\);
-
5.
\(\{\varPi (q), \alpha (q)\}\; {\leftarrow }\; {{\texttt {\textit{query}}}}(q, D_h, {{\texttt {\textit{auth}}}}(D_{h}), \mathtt{pk})\): On input of a query q on data structure \(D_h\), the authenticated data structure \({{\texttt {\textit{auth}}}}(D_{h})\) and the public key \(\mathtt{pk}\), it returns the answer \(\alpha (q)\) to the query, along with proof \(\varPi (q)\);
-
6.
{accept, reject} \({\leftarrow }\) verify \((q,~\alpha ,~\varPi ,\mathsf{s}_{h},~\mathtt{pk})\): On input of a query q, an answer \(\alpha \), a proof \(\varPi \), a snapshot \(\mathsf{s}_h\) and the public key \(\mathtt{pk}\), it outputs either accept or reject.
Next to the definition of the ADS scheme, another algorithm was defined for deciding whether or not an answer \(\alpha \) to query q on data structure \(D_h\) is correct: {accept, reject} \({\leftarrow }\) check \((q,\alpha ,D_h)\).
Definition 2
(Correctness). Let \(\mathcal {A}\) be an ADS scheme {genkey,setup, update,refresh,query,verify}. The ADS scheme \(\mathcal {A}\) is correct if, for all \(\lambda \in \mathbb {N}\), for all {\(\mathtt{sk}, \mathtt{pk}\)} output by algorithm genkey, for all \(D_h\), auth \((D_h)\), \(\mathsf{s}_h\) output by one invocation of setup followed by polynomially-many invocations of refresh, where \(h \ge 0\), for all queries q and for all \(\varPi (q),\alpha (q)\) output by query \((q,D_h, {\texttt {\textit{auth}}}(D_{h}),\mathtt{pk})\) with all but negligible probability, whenever algorithm check \((q,\alpha (q),D_h)\) outputs accept, so does verify \((q,\alpha (q),\varPi (q),\mathsf{s}_h,\mathtt{pk})\).
Definition 3
(Security). Let \(\mathcal {A}\) be an ADS scheme {genkey,setup,update, refresh,query,verify}, \(\lambda \) be the security parameter, \(\epsilon (\lambda )\) be a negligible function and {\(\mathtt{sk},\mathtt{pk}\)} \({\leftarrow }\) genkey \((1^\lambda )\). Let also \(\mathbf {Adv}\) be a probabilistic polynomial-time adversary that is only given \(\mathtt{pk}\). The adversary has unlimited access to all algorithms of \(\mathcal {A}\), except for algorithms setup and update to which he has only oracle access. The adversary picks an initial state of the data structure \(D_0\) and computes \(D_0,{{\texttt {\textit{auth}}}}(D_{0}),\mathsf{s}_0\) through oracle access to algorithm setup. Then, for \(i=0, ...,h = {{\texttt {\textit{poly}}}}(\lambda )\), \(\mathbf {Adv}\) issues an update \(u_i\) in the data structure \(D_i\) and computes \(D_{i+1},{{\texttt {\textit{auth}}}}(D_{i+1})\) and \(\mathsf{s}_{i+1}\) through oracle access to algorithm update. Finally the adversary picks an index \(0 \le t \le h+1\), and computes a query q, answer \(\alpha \) and proof \(\varPi \). The ADS scheme \(\mathcal {A}\) is secure if for all \(\lambda \in \mathbb {N}\), for all {\(\mathtt{sk},\mathtt{pk}\)} output by algorithm genkey, and for any probabilistic polynomial-time adversary \(\mathbf {Adv}\) it holds that

2.2 History Tree
A tamper-evident history system, as defined by Crosby and Wallach [6], consists of a history tree data structure and five algorithms. A history tree is in essence a versioned Merkle tree [15] (hash tree). Each leaf node in the tree is the hash of an event, while interior nodes are labeled with the hash of its children nodes in the subtree rooted at that node. The root of the tree fixes the content of the entire tree. Different versions of history trees, produced as events are added, can be proven to make consistent claims about the past. The five algorithms, adjusted to our terminology, are defined as follows:
-
\(c_i {\leftarrow }\) H.Add(e): Given an event e the system appends it to the history tree H as the i:th event and then outputs a commitmentFootnote 1 \(c_i\).
-
{\(P, e_i\)} \({\leftarrow }\) H.MembershipGen(i, \(c_j\)): Generates a membership proof P for the i:th event with respect to commitment \(c_j\), where \(i \le j\), from the history tree H. The algorithm outputs P and the event \(e_i\).
-
\(P \; {\leftarrow }\; \mathtt{H.IncGen} (c_i, c_j)\): Generates an incremental proof P between \(c_i\) and \(c_j\), where \(i \le j\), from the history tree H. Outputs P.
-
{accept, reject} \({\leftarrow }\; {\mathtt{P.MembershipVerify}}(i, c_j ,e'_i)\): Verifies that P proves that \(e'_i\) is the i:th event in the history defined by \(c_j\) (where \(i \le j\)). Outputs \(\mathtt{accept}\) if true, otherwise \(\mathtt{reject}\).
-
{accept, reject} \({\leftarrow }\) P.IncVerify \((c'_i, c_j)\): Verifies that P proves that \(c_j\) fixes every event fixed by \(c'_i\) (where \(i \le j\)). Outputs \(\mathtt{accept}\) if true, otherwise \(\mathtt{reject}\).
2.3 Hash Treap
A treap is a type of randomised binary search tree [2], where the binary search tree is balanced using heap priorities. Each node in a treap has a key, value, priority, left child and right child. A treap has three important properties:
-
1.
Traversing the treap in order gives the sorted order of the keys;
-
2.
Treaps are structured according to the nodes’ priorities, where each node’s children have lower priorities;
-
3.
Given a deterministic attribution of priorities to nodes, a treap is set unique and history independent, i.e., its structure is unique for a given set of nodes, regardless of the order in which nodes were inserted, and the structure does not leak any information about the order in which nodes were inserted.
When a node is inserted in a treap, its position in the treap is first determined by a binary search. Once the position is found, the node is inserted in place, and then rotated upwards towards the root until its priority is consistent with the heap priority. When the priorities are assigned to nodes using a cryptographic hash function, the tree becomes probabilistically balanced with an expected depth of \(\log {n}\), where n is the number of nodes in the treap. Inserting a node takes expected \(\mathcal {O}(\text {log}\,n)\) operations and results in expected \(\mathcal {O}(1)\) rotations to preserve the properties of the treap [9]. Given a treap, it is straightforward to build a hash treap: have each node calculate the hash of its own attributesFootnote 2 together with the hash of its children. Since the hash treap is a Merkle tree, its root fixes the entire hash treap. The concept of turning treaps into Merkle trees for authenticating the treap has been used for example in the context of persistent authenticated dictionaries [7] and authentication of certificate revocation lists [18].
We define the following algorithms on our hash treap, for which we assume that keys k are unique and of predefined constant size cst:
-
\(r \; {\leftarrow }\) T.Add(k, v): Given a unique key k and value v, where \(|k| = cst\) and \(|v| > 0\), the system inserts them into the hash treap T and then outputs the updated hash of the root r. The add is done with priority \({\mathtt{Hash}}(k)\), which results in a deterministic treap. After the new node is in place, the hash of each node along the path from the root has its internal hash updated. The hash of a node is \({\mathtt{Hash}}\big (k|| v || \text {left.hash}||\text {right.hash}\big )\). In case there is no right (left) child node, the right.hash (left.hash) is set to a string of consecutive zeros of size equal to the output of the used hash function \(0^{|{\mathtt{Hash}}(\cdot )|}\).
-
{\(P^T, v\)} \({\leftarrow }\) T.AuthPath(k): Generates an authenticated path \(P^T\) from the root of the treap T to the key k where \(|k| = cst\). The algorithm outputs \(P^T\) and, in case of when a node with key k was found, the associated value v. For each node i in \(P^T\), \(k_i\) and \(v_i\) need to be provided to verify the hash in the authenticated path.
-
{accept, reject} \({\leftarrow }\) P \(^{T}\) .AuthPathVerify(k,v): Verifies that \(P^T\) proves that k is a non-member if
 or otherwise a member. Verification checks that \(|k| = cst\) and \(|v| > 0\) (if \(\ne \mathtt{null}\)), calculates and compares the authenticator for each node in \(P^T\), and checks that each node in \(P^T\) adheres to the sorted order of keys and heap priority.
or otherwise a member. Verification checks that \(|k| = cst\) and \(|v| > 0\) (if \(\ne \mathtt{null}\)), calculates and compares the authenticator for each node in \(P^T\), and checks that each node in \(P^T\) adheres to the sorted order of keys and heap priority.
Additionally we define the following helper algorithms on our hash treap:
-
pruned(T) \({\leftarrow }\) T.BuildPrunedTree(\(<P^{T}_{j}>)\): Generates a pruned hash treap \(\mathtt{pruned(T)}\) from the given authenticated paths \(P^T_j\) in the hash treap T. This algorithm removes any redundancy between the authenticated paths, resulting in a more compact representation as a pruned hash treap. Note that evaluating pruned(T).AuthPathVerify(k, v) is equivalent with evaluating \(\mathtt{P}^T\mathtt{.AuthPath} \mathtt{Verify}(k,v)\) on the authenticated path P\(^T\) through k contained in the pruned hash treap.
-
\(r \; {\leftarrow }\; {\mathtt{P}}^{T}\mathtt{.root}()\): Outputs the root r of an authenticated path. Note that pruned(T).root() and \(\mathtt{P}^{T}\mathtt{.root}()\) are equivalent for any authenticated path P\(^T\) contained by the pruned tree.
2.4 Cryptographic Building Blocks
We assume idealised cryptographic building blocks in the form of a hash function \({\mathtt{Hash}}(\cdot )\), and signature scheme that is used to sign a message m and verify the resulting signature: {accept, reject} \({\leftarrow }\; {\mathtt{Verify}}_{\mathtt{vk}}\big ({\mathtt{Sign}}_{\mathtt{sk}}(m), m\big )\). The hash function should be collision and pre-image resistant. The signature scheme should be existentially unforgeable under known message attack. Furthermore, we rely on the following lemma for the correctness and security of a Balloon:
Lemma 1
The security of an authenticated path in a Merkle (hash) tree reduces to the collision resistance of the underlying hash function.
Proof
This follows from the work by Merkle [16] and Blum et al. [5]. \(\square \)
3 Construction and Algorithms
Our data structure is an append-only key-value store that stores events e consisting of a key k and a value v. Each key \(k_i\) is assumed to be unique and of predefined constant size cst, where \(cst \; {\leftarrow }\; |{\mathtt{Hash}}(\cdot )|\). Additionally, our data structure encodes some extra information in order to identify in which set (epoch) events were added. We define an algorithm \(k \; {\leftarrow }\) key(e) that returns the key k of the event e.
Our authenticated data structure combines a hash treap and a history tree when adding an event an event e as follows:
-
First, the event is added to the history tree: \(c_i \; {\leftarrow }\; H.add\big ({\mathtt{Hash}}(k||v)\big )\). Let i be the index where the hashed event was inserted at into the history tree.
-
Next, the hash of the event key \({\mathtt{Hash}}(k)\) and the event position i are added to the hash treap: \(r \; {\leftarrow }\; \mathtt{T.Add}({\mathtt{Hash}}(k),i)\).
Figure 1 visualises a simplified Balloon with a hash treap and a history tree. For the sake of readability, we omit the hash values and priority, replace hashed keys with integers, and replace hashed events with place-holder labels. For example, the root in the hash treap has key 42 and value 1. The value 1 refers to the leaf node in the history tree with index 1, whose value is p42, the place-holder label for the hash of the event which key, once hashed, is represented by integer 42.
By putting the hash of the event key, \({\mathtt{Hash}}(k)\), instead of the key into the hash treap, we avoid easy event enumeration by third parties: no valid event keys leak as part of authenticated paths in the treap for non-membership proofs. Note that when H.MembershipGen returns an event, as specified in Sect. 2.2, the actual event is retrieved from the data structure, not the hash of the event as stored in the history tree (authentication). We store the hash of the event in the history tree for sake of efficiency, since the event is already stored in the (non-authenticated) data structure.
3.1 Setup
Algorithm. {\(\mathtt{sk}, \mathtt{pk}\)} \({\leftarrow }\) genkey(\(1^\lambda ):\) Generates a signature key-pair {\(\mathtt{sk}, \mathtt{vk}\)} using the generation algorithm of a signature scheme with security level \(\lambda \) and picks a function \(\varOmega \) that deterministically orders events. Outputs the signing key as the private key \(\mathtt{sk}= \mathtt{sk}\), and the verification key and the ordering function \(\varOmega \) as the public key \(\mathtt{pk}= \{\mathtt{vk}, \varOmega \}\).
Algorithm. {\({\mathtt{auth}(D_{0})},\mathsf{s}_0\)} \({\leftarrow }\) setup(\(D_0,\mathtt{sk},\mathtt{pk}\)): Let \(D_0\) be the initial data structure, containing the initial set of events \(<e_j>\). The authenticated data structure, \({\mathtt{auth}(D_{0})}\), is then computed by adding each event from the set to the, yet empty, authenticated data structure in the order dictated by the function \(\varOmega \; {\leftarrow }\; \mathtt{pk}\). The snapshot is defined as the root of the hash treap r and commitment in the history tree \(c_i\) for the event that was added last together with a digital signature over those: \(\mathsf{s}_{0} = \{r,c_i, \sigma \}\), where \(\sigma = {\mathtt{Sign}}_\mathtt{sk}(\{r,c_i\})\).
3.2 Update and Refresh
Algorithm. {\(D_{h+1}, {\mathtt{auth}(D_{h+1})}, \mathsf{s}_{h+1}, upd\)} \({\leftarrow }\) update(u, \(D_h, {\mathtt{auth}(D_{h})}, \mathsf{s}_h, \mathtt{sk}, \mathtt{pk}\)): Let u be a set of events to insert into \(D_h\). The updated data structure \(D_{h+1}\) is the result of appending the events in u to \(D_h\) and indicating that these belong the \({(h+1)^{\text {th}}}\) set. The updated authenticated data structure, \({\mathtt{auth}(D_{h+1})}\), is then computed by adding each event from the set to the authenticated data structure \({\mathtt{auth}(D_{h})}\) in the order dictated by the function \(\varOmega \; {\leftarrow }\; \mathtt{pk}\). The updated snapshot is the root of the hash treap r and commitment in the history tree \(c_i\) for the event that was added last together with a digital signature over those: \(\mathsf{s}_{h+1} = \{r,c_i, \sigma \}\), where \(\sigma = {\mathtt{Sign}}_\mathtt{sk}(\{r,c_i\})\). The update information contains this snapshot \(upd = \mathsf{s}_{h+1}\).
Algorithm. {\( D_{h+1}, {\mathtt{auth}(D_{h+1})}, \mathsf{s}_{h+1}\)} \({\leftarrow }\) refresh(u, \(D_h, {\mathtt{auth}(D_{h})}, \mathsf{s}_h, upd, \mathtt{pk}\)): Let u be a set of events to insert into \(D_h\). The updated data structure \(D_{h+1}\) is the result of appending the events in u to \(D_h\) and indicating that these belong the \({(h+1)^{\text {th}}}\) set. The updated authenticated data structure, \({\mathtt{auth}(D_{h+1})}\), is then computed by adding each event from the set u to the authenticated data structure \({\mathtt{auth}(D_{h})}\) in the order dictated by the function \(\varOmega \; {\leftarrow }\; \mathtt{pk}\). Finally, the new snapshot is set to \(\mathsf{s}_{h+1} = upd\).
3.3 Query and Verify
Algorithm. {\(\varPi (q), \alpha (q)\)} \({\leftarrow }\) query(q, \(D_h, {\mathtt{auth}(D_{h})}, \mathtt{pk}\)) (Membership): We consider the query q to be “a membership query for an event with key k in the data structure that is fixed by \(\mathsf{s}_{queried}\)”, where \(queried \le h\). The query has two possible answers \(\alpha (q)\): {\(\mathtt{true}, e\)} in case an event e with key k exists in \(D_{queried}\), otherwise false. The proof of correctness \(\varPi (q)\) consists of up to three parts:
-
1.
An authenticated path \(P^T\) in the hash treap to \(k' = {\mathtt{Hash}}(k)\);
-
2.
The index i of the event in the history tree;
-
3.
A membership proof P on index i in the history tree.
The algorithm generates an authenticated path in the hash treap, which is part of \({\mathtt{auth}(D_{h})}\), to \(k'\): {\(P^T,v\)} \({\leftarrow }\) T.AuthPath(k’). If  , then there is no event with key k in \(D_{h}\) (and consequently in \(D_{queried}\)) and the algorithm outputs \(\varPi (q) = P^T\) and \(\alpha (q) = \mathtt{false}\).
, then there is no event with key k in \(D_{h}\) (and consequently in \(D_{queried}\)) and the algorithm outputs \(\varPi (q) = P^T\) and \(\alpha (q) = \mathtt{false}\).
Otherwise, the value v in the hash treap indicates the index i in the history tree of the event. Now the algorithm checks whether or not the index i is contained in the history tree up till \({\mathtt{auth}(D_{queried})}\). If not, the algorithm outputs \(\alpha (q) = \mathtt{false}\) and \(\varPi (q)\) = {\(P^T, i\)}. If it is, the algorithm outputs \(\alpha (q)\) = {true,\(e_i\)} and \(\varPi (q)\) = {\(P^T, i, P\)}, where {\(P, e_i\)} \({\leftarrow }\) H.MembershipGen(i, \(c_{queried}\)) and \(c_{queried} \; {\leftarrow }\; \mathsf{s}_{queried}\).
Algorithm. {\(\mathtt{accept}, \mathtt{reject}\)} \({\leftarrow }\) verify(q, \(\alpha , \varPi , \mathsf{s}_h, \mathtt{pk}\)) (Membership): First, the algorithm extracts {\(k, \mathsf{s}_{queried}\)} from the query q and {\(P^T, i, P\)} from \(\varPi \), where i and P can be null. From the snapshot it extracts \(r \; {\leftarrow }\; \mathsf{s}_h\). Then the algorithm computes \(x \;{\leftarrow }\; \mathtt{P}^{T}\mathtt{.AuthPathVerify}(k,i)\). If  false \(\vee ~ \mathtt{P}^{T}\mathtt{.root}() \ne r\), the algorithm outputs reject. The algorithm outputs accept if any of the following three conditions hold, otherwise reject:
false \(\vee ~ \mathtt{P}^{T}\mathtt{.root}() \ne r\), the algorithm outputs reject. The algorithm outputs accept if any of the following three conditions hold, otherwise reject:
-
 \(\wedge \)
\(\wedge \)  ;
; -
 \(\wedge \) \(i > queried[-1]\)
Footnote 3 ;
\(\wedge \) \(i > queried[-1]\)
Footnote 3 ; -
 \(\wedge \) key
\(\wedge \) key 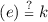 \(\wedge \)
\(\wedge \)  ,
,for \(y \; {\leftarrow }\; P \mathtt{.MembershipVerify}(i, c_{queried} ,{\mathtt{Hash}}(e))\) and \(c_{queried} \; {\leftarrow }\; \mathsf{s}_{queried}\) .
4 Security
Theorem 1
Balloon {genkey,setup,update,refresh,query,verify} is a correct ADS scheme for a data structure D, that contains a list of sets of events, according to Definition 2, assuming the collision-resistance of the underlying hash function.
The proof of correctness can be found in the full version of our paper [20].
Theorem 2
Balloon {genkey,setup,update,refresh,query,verify} is a secure ADS scheme for a data structure D, that contains a list of sets of events, according to Definition 3, assuming the collision-resistance of the underlying hash function.
The full proof of security can be found in Appendix A.
Proof
(Sketch). Given that the different versions of the authenticated data structure and corresponding snapshots are generated through oracle access, these are correct, i.e., the authenticated data structure contains all elements of the data structure for each version, the root and commitment in each snapshot correspond to that version of the ADS and the signature in each snapshot verifies.
For all cases where the check algorithm outputs reject, \(\mathbf {Adv}\) has to forge an authenticated path in the hash treap and/or history tree in order to get the verify algorithm to output accept, which implies breaking Lemma 1.
5 Verifiable Insert
In practical three-party settings, the source typically has less storage capabilities than servers. As such, it would be desirable that the source does not need to keep a copy of the entire (authenticated) data structure for update, but instead can rely on its own (constant) storage combined with verifiable information from a server. We define new query and verify algorithms that enable the construction of a pruned authenticated data structure, containing only the nodes needed to be insert the new set of events with a modified update algorithm. The pruned authenticated data structure is denoted by \({\mathtt{pruned}\big ({\mathtt{auth}(D_{h})},u\big )}\), where \({\mathtt{auth}(D_{h})}\) denotes the version of the ADS being pruned, and u the set of events where this ADS is pruned for.
Algorithm. {\(\varPi (q), \alpha (q)\)} \({\leftarrow }\) query(q, \(D_h, {\mathtt{auth}(D_{h})}, \mathtt{pk}\)) (Prune): We consider the query q to be “a prune query for if a set of events u can be inserted into \(D_h\)”. The query has two possible answers: \(\alpha (q)\): true in case no key for the events in u already exist in \(D_h\), otherwise false. The proof of correctness \(\varPi (q)\) either proves that there already is an event with a key from an event in u, or provides proofs that enable the construction of a pruned \({\mathtt{auth}(D_{h})}\), depending on the answer. For every \(k_j \; {\leftarrow }\; \mathtt{key}(e_j)\) in the set u, the algorithm uses as a sub-algorithm {\(\varPi '_j(q), \alpha '_j(q)\)} \({\leftarrow }\) query \((q'_j, D_h, {\mathtt{auth}(D_{h})}, \mathtt{pk})\) (Membership) with \(q = \{k_j,\mathsf{s}_h\}\), where \(\mathsf{s}_h\) fixes \({\mathtt{auth}(D_{h})}\). If any  , the algorithm outputs \(\alpha (q) = \mathtt{false}\) and \(\varPi (q) = \{\varPi '_j(q), k_j\}\) and stops. If not, the algorithm takes P\(^T_j\) from each \(\varPi '_j(q)\) and creates the set \(<P^T_j>\). Next, the algorithm extracts the latest event \(e_i\) inserted into the history tree from \({\mathtt{auth}(D_{h})}\) and uses as a sub-algorithm {\(\varPi '(q), \alpha '(q)\)} \({\leftarrow }\) query \((q', D_h, {\mathtt{auth}(D_{h})}, \mathtt{pk})\) (Membership) with q’ = {key \((e_i), \mathsf{s}_h\)}. Finally, the algorithm outputs \(\alpha (q) = \mathtt{true}\) and \(\varPi (q) = \{<P^T_j>,\varPi '(q)\}\).
, the algorithm outputs \(\alpha (q) = \mathtt{false}\) and \(\varPi (q) = \{\varPi '_j(q), k_j\}\) and stops. If not, the algorithm takes P\(^T_j\) from each \(\varPi '_j(q)\) and creates the set \(<P^T_j>\). Next, the algorithm extracts the latest event \(e_i\) inserted into the history tree from \({\mathtt{auth}(D_{h})}\) and uses as a sub-algorithm {\(\varPi '(q), \alpha '(q)\)} \({\leftarrow }\) query \((q', D_h, {\mathtt{auth}(D_{h})}, \mathtt{pk})\) (Membership) with q’ = {key \((e_i), \mathsf{s}_h\)}. Finally, the algorithm outputs \(\alpha (q) = \mathtt{true}\) and \(\varPi (q) = \{<P^T_j>,\varPi '(q)\}\).
Algorithm. {\(\mathtt{accept}, \mathtt{reject}\)} \({\leftarrow }\) verify(q,\(\alpha ,\varPi ,\mathsf{s}_h,\mathtt{pk}\)) (Prune): The algorithm starts by extracting \(< e_j > \; {\leftarrow }\; u\) from the query q. If  , it gets {\(\varPi '_j(q), k_j\)} from \(\varPi \) and uses as a sub-algorithm \(\mathtt{valid} \; {\leftarrow }\; \mathtt{verify}(q',\alpha ',\varPi ',\mathsf{s}_h, \mathtt{pk})\) (Membership), with q’ = {\(k,\mathsf{s}_h\)}, \(\alpha ' = \mathtt{true}\) and \(\varPi ' = \varPi '_j(q)\), where \(k \; {\leftarrow }\; k_j\). If
, it gets {\(\varPi '_j(q), k_j\)} from \(\varPi \) and uses as a sub-algorithm \(\mathtt{valid} \; {\leftarrow }\; \mathtt{verify}(q',\alpha ',\varPi ',\mathsf{s}_h, \mathtt{pk})\) (Membership), with q’ = {\(k,\mathsf{s}_h\)}, \(\alpha ' = \mathtt{true}\) and \(\varPi ' = \varPi '_j(q)\), where \(k \; {\leftarrow }\; k_j\). If  and there exists an event with key k in u, the algorithm outputs accept, otherwise reject.
and there exists an event with key k in u, the algorithm outputs accept, otherwise reject.
If  , extract {\(<\mathrm{P}^{T}_{j}>,\varPi '(q)\)} from \(\varPi \). For each event \(e_j\) in u, the algorithm gets \(k_j \; {\leftarrow }\; \mathtt{key}(e_j)\), finds the corresponding \(\mathrm{P}^T_j\) for \(k'_j = {\mathtt{Hash}}(k_j)\), and uses as a sub-algorithm \(\mathtt{valid} \; {\leftarrow }\; \mathtt{verify}(q',\alpha ',\varPi ',\mathsf{s}_h,\mathtt{pk})\) (Membership), with \(q' = \{k_j,\mathsf{s}_h\)}, \(\alpha ' = \mathtt{false}\) and \(\varPi ' = \mathrm{P}^{T}_j\). If no corresponding \(\mathrm{P}^{T}_j\) to \(k'_j\) is found in \(<\mathrm{P}^T_j>\) or valid
, extract {\(<\mathrm{P}^{T}_{j}>,\varPi '(q)\)} from \(\varPi \). For each event \(e_j\) in u, the algorithm gets \(k_j \; {\leftarrow }\; \mathtt{key}(e_j)\), finds the corresponding \(\mathrm{P}^T_j\) for \(k'_j = {\mathtt{Hash}}(k_j)\), and uses as a sub-algorithm \(\mathtt{valid} \; {\leftarrow }\; \mathtt{verify}(q',\alpha ',\varPi ',\mathsf{s}_h,\mathtt{pk})\) (Membership), with \(q' = \{k_j,\mathsf{s}_h\)}, \(\alpha ' = \mathtt{false}\) and \(\varPi ' = \mathrm{P}^{T}_j\). If no corresponding \(\mathrm{P}^{T}_j\) to \(k'_j\) is found in \(<\mathrm{P}^T_j>\) or valid  , then the algorithm outputs reject and stops. Next, the algorithm uses as a sub-algorithm \(\mathtt{valid} \; {\leftarrow }\; \mathtt{verify}(q',\alpha ,\varPi ',\mathsf{s}_h,\mathtt{pk})\) (Membership), with \(q' = \){key \((e_i),\mathsf{s}_h\)} and \(\varPi ' = \varPi '(q)\), where \(e_i \in \varPi '(q)\). If valid
, then the algorithm outputs reject and stops. Next, the algorithm uses as a sub-algorithm \(\mathtt{valid} \; {\leftarrow }\; \mathtt{verify}(q',\alpha ,\varPi ',\mathsf{s}_h,\mathtt{pk})\) (Membership), with \(q' = \){key \((e_i),\mathsf{s}_h\)} and \(\varPi ' = \varPi '(q)\), where \(e_i \in \varPi '(q)\). If valid  and
and  the algorithm outputs accept, otherwise reject.
the algorithm outputs accept, otherwise reject.
Algorithm. {\(\mathsf{s}_{h+1},upd\)} \({\leftarrow }\) update*(u, \(\varPi , \mathsf{s}_h, \mathtt{sk},\mathtt{pk}\)): Let u be a set of events to insert into \(D_h\) and \(\varPi \) a proof that the sub-algorithm \(\mathtt{verify}(q,\alpha ,\varPi ,\) \(\mathsf{s}_h,\mathtt{pk})\) (Prune) outputs accept for, where \(q = u\) and \(\alpha = \mathtt{true}\). The algorithm extracts {\(<\mathrm{P}^T_j>,\varPi '(q)\)} from \(\varPi \) and builds a pruned hash treap \(\mathtt{pruned}(T) \; {\leftarrow }\; \mathtt{T.Build} \mathtt{PrunedTree}(<\mathrm{P}^T_j>)\). Next, it extracts P from \(\varPi '(q)\) and constructs the pruned Balloon \({\mathtt{pruned}\left( {\mathtt{auth}(D_{h})},u\right) }\) \({\leftarrow }\) {pruned(T), P}. Finally, the algorithm adds each event in u to the pruned Balloon \({\mathtt{pruned}\big ({\mathtt{auth}(D_{h})},u\big )}\) in the order dictated by \(\varOmega \; {\leftarrow }\; \mathtt{pk}\). The updated snapshot is the digital signature over the root of the updated pruned hash treap r and commitment in the updated pruned history tree \(c_i\) for the event that was added last: \(\mathsf{s}_{h+1} = \{r,c_i\},{\mathtt{Sign}}_\mathtt{sk}(\{r,c_i\)}). The update information contains this snapshot \(upd = \mathsf{s}_{h+1}\).
Lemma 2
The output of \({{\texttt {\textit{update}}}}\) and \({{\texttt {\textit{update*}}}}\) is identical with respect to the root of the hash treap and the latests commitment in the history tree of \(\mathsf{s}_{h+1}\) and upd Footnote 4.
The proof of Lemma 2 can be found in the full version of our paper [20]. As a result of Lemma 2, the update algorithm in Balloon can be replaced by update* without breaking the correctness and security of the Balloon as in Theorems 1 and 2. This means that the server can keep and refresh the (authenticated) data structure while the author only needs to store the last snapshot \(s_h\) to be able to produce updates, resulting in a small constant size storage requirement for the author.
Note that, in order to reduce the size of the transmitted proof, verify (Prune) could output the pruned authenticated data structure directly. Since pruned(T). AuthPathVerify(k, v) and \(\mathtt{P}^{T}\mathtt{.AuthPathVerify}(k,v)\) are equivalent, the correctness and security of verify (Prune) reduce to verify (Mem-bership). Section 7 shows the reduction in the size of the proof with pruning.
6 Publicly Verifiable Consistency
While the server is untrusted, the author is trusted. A stronger adversarial model assumes forward security for the author: the author is only trusted up to a certain point in time, i.e., the time of compromise, and afterwards cannot change the past. In this stronger adversarial model, Balloon should still provide correctness and security for all events inserted by the author up till the time of author compromise.
Efficient incremental proofs, realised by the IncGen and IncVerify algorithms, are a key feature of history trees [9]. Anyone can challenge the server to provide a proof that one commitment as part of a snapshot is consistent with all previous commitments as part of snapshots. However, it appears to be an open problem to have an efficient algorithm for showing consistency between roots of different versions of a treap (or any lexicographically sorted data structure) [8]. In Appendix B, we show why one cannot efficiently use probabilistic proofs of consistency for a Balloon. In absence of efficient (both for the server and verifier in terms of computation, storage, and size) incremental proofs in hash treaps, we rely on a concept from Certificate Transparency [12]: monitors.
We assume that a subset of clients, or any third party, will take on a role referred to as a “monitor”, “auditor”, or “validator” in, e.g., [3, 10–12, 22, 27]. A monitor continuously monitors all data stored at a server and ensures that all snapshots issued by an author are consistent. We assume that clients and monitors receive the snapshots through gossiping.
Definition 4
(Publicly Verifiable Consistency). An ADS scheme is publicly verifiable consistent if anyone can verify that a set of events u has been correctly inserted in \(D_h\) and \({\texttt {\textit{auth}}}(D_{h})\), fixed by \(\mathsf{s}_h\) to form \(D_{h+1}\) and \({{\texttt {\textit{auth}}}}(D_{h+1})\) fixed by \(\mathsf{s}_{h+1}\).
Algorithm. {\(\alpha , D_{h+1}, {\mathtt{auth}(D_{h+1})}, \mathsf{s}_{h+1}\)} \({\leftarrow }\) refreshVerify(u, \(D_h, \, {\mathtt{auth}(D_{h})}, \mathsf{s}_h, \; upd, \mathtt{pk}\)): First, the algorithm runs {\(D_{h+1}, {\mathtt{auth}(D_{h+1})}, \mathsf{s}_{h+1}\)} \({\leftarrow }\) refresh(u, \(D_h, {\mathtt{auth}(D_{h})}, \mathsf{s}_h, upd, \mathtt{pk}\)) as a sub-algorithm. Then, the algorithm verifies the updated snapshot {\(r,c_i,\sigma \)} \({\leftarrow }\; \mathsf{s}_{h+1}\; {\leftarrow }\; upd\):
-
verify the signature:
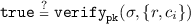 ; and
; and -
match the root of the updated hash treap
 ; and
; and -
match the last commitment in the updated history tree
 .
.
If the verify succeeds, the algorithm outputs {\(\alpha = \mathtt{true}, D_{h+1}, {\mathtt{auth}(D_{h+1})}, \mathsf{s}_{h+1}\)}. Otherwise, the algorithm outputs \(\alpha = \mathtt{false}\).
Theorem 3
With refreshVerify, Balloon is publicly verifiable consistent according to Definition 4, assuming perfect gossiping of the snapshots and the collision-resistance of the underlying hash function.
The proof of publicly verifiable consistency can be found in the full version of our paper [20]. Note that for the purpose of verifying consistency between snapshots, it is not necessary to keep the data structure D. Moreover, the storage requirement for monitors can be further reduced by making use of pruned versions of the authenticated data structure, i.e., by using a \(\mathtt{refresh}^*\) sub-algorithm, similar to the \(\mathtt{update}^*\) algorithm. Finally, to preserve event privacy towards monitors, one can provide the monitors with \(\tilde{u} =\, <\tilde{e_j}>\), where \( \tilde{e_j} = \big ({\mathtt{Hash}}(k_j),{\mathtt{Hash}}(e_j)\big )\), and not the actual set of events. However, in this case, one must ensure that the ordering function \(\varOmega \; {\leftarrow }\; \mathtt{pk}\) provides the same output for u and \(\tilde{u}\).
7 Performance
We implemented Balloon in the GoFootnote 5 programming language using SHA-512 as the hash function and Ed25519 for signatures [4]. The output of SHA-512 is truncated to 256-bits, with the goal of reaching a 128-bits security level. The source code and steps to reproduce our results are available at http://www.cs.kau.se/pulls/balloon/. Our performance evaluation focuses on verifiable inserts, which are composed of performing and verifying \(|u|+1\) membership queries, since these algorithms presumably are the most common. Figure 2 shows the size of the proof from query (Prune) in KiB based on the number of events to insert ranging from 1–1000 for three different sizes of Balloon: \(2^{10}\), \(2^{15}\), and \(2^{20}\) events. Figure 2a includes redundant nodes in the membership query proofs, and shows that the proof size is linear with the number of events to insert. Figure 2b excludes redundant nodes between proofs, showing that excluding redundant nodes roughly halves the proof size with bigger gains the more events are inserted. For large Balloons the probability that any two authenticated paths in the hash treap share nodes goes down, resulting in bigger proofs, until the number of events get closer to the total size of the Balloon, when eventually all nodes in the hash treap are included in the proof as for the \(2^{10}\) Balloon.
Table 1 shows a micro-benchmark of the three algorithms that enable verifiable inserts: query(Prune), verify(Prune), and update*. The table shows the average insert time (ms) calculated by Go’s built-in benchmarking tool that performed between 30–30000 samples per measurement. The update* algorithm performs the bulk of the work, with little difference between the different Balloon sizes, and linear scaling for all three algorithms based on the number of events to insert.
8 Related Work
Balloon is closely related to authenticated dictionaries [18] and persistent authenticated dictionaries (PADs) [1, 7, 8]. Balloon is not a PAD because it does not allow for the author to remove or update keys from the data structure, i.e., it is append-only. By allowing the removal of keys, the server needs to be able to construct past versions of the PAD to calculate proofs, which is relatively costly. In Table 2, Balloon is compared to the most efficient tree-based PAD construction according to Crosby & Wallach [8]: a red-black tree using Sarnak-Tarjan versioned nodes with a cache-everywhere strategy for calculated hash values. The table shows expected complexity. Note that red-black trees are more efficient than treaps due to their worst-case instead of expected logarithmic bounds on several important operations. We opted for using a treap due to its relative simplicity. For Balloon, the storage at the author is constant due to using verifiable inserts, while the PAD maintains a copy of the entire data structure. To query past versions, the PAD has to construct past versions of the data structure, while Balloon does not. When inserting new events, the PAD has to store a copy of the modified authenticated path in the red-black tree, while the storage for Balloon is constant. However, Balloon is less efficient when inserting new events with regard to the proof size due to verifiable inserts.
Miller et al. [17] present a generic method for authenticating operations on any data structure that can be defined by standard type constructors. The prover provides the authenticated path in the data structure that are traversed by the prover when performing an operation. The verifier can then perform the same operation, only needing the authenticated paths provided in the proof. The verifier only has to store the latest correct digest that fixes the content of the data structure. Our verifiable insert is based on the same principle.
Secure logging schemes, like the work by Schneier and Kelsey [23], Ma and Tsudik [13], and Yavuz et al. [21] can provide deletion detection and forward-integrity in a forward secure model for append-only data. Some schemes, like that of Yavuz et al., are publicly verifiable like Balloon. However, these schemes are insufficient in our setting, since clients cannot get efficient non-membership proofs, nor efficient membership-proofs for past versions of the data structure when only some versions (snapshots) are timestamped.
All the following related work operates in a setting that is fundamentally different to the one of Balloon. For Balloon, we assume a forward-secure author with an untrusted server, whereas the following related work assumes a (minimally) trusted server with untrusted authors.
Certificate Transparency [12] and the tamper-evident history system by Crosby & Wallach [6] use a nearly identicalFootnote 6 data structure and operations. Even though in both Certificate Transparency and Crosby & Wallach’s history system, a number of minimally trusted authors insert data into a history tree kept by a server, clients query the server for data and can act as auditors or monitors to challenge the server to prove consistency between commitments. Non-membership proofs require the entire data structure to be sent to the verifier.
In Revocation Transparency, Laurie and Kasper [11] present the use of a sparse Merkle tree for certificate revocation. Sparse Merkle trees create a Merkle tree with \(2^N\) leafs, where N is the bit output length of a hash algorithm. A leaf is set to 1 if the certificate with the hash value fixed by the path to the leaf from the root of the tree is revoked, and 0 if not. While the tree in general is too big to store or compute on its own, the observation that most leafs are zero (i.e., the tree is sparse) means that only paths including non-zero leafs need to be computed and/or stored. At first glance, sparse Merkle trees could replace the hash treap in a Balloon with similar size/time complexity operations.
Enhanced Certificate Transparency (ECT) by Ryan [22] extends CT by using two data structures: one chronologically sorted and one lexicographically sorted. Distributed Transparent Key Infrastructure (DTKI) [27] builds upon the same data structures as ECT. The chronologically sorted data structure corresponds to a history tree (like CT). The lexicographically sorted data structure is similar to our hash treap. For checking consistency between the two data structures, ECT and DTKI use probabilistic checks. The probabilistic checking verifies that a random operation recorded in the chronological data structure has been correctly performed in the lexicographical data structure. However, this requires the prover to generate past versions of the lexicographical data structure (or cache all proofs), with similar trade-offs as for PADs, which is relatively costly.
CONIKS [14] is a privacy-friendly key management system where minimally trusted clients manage their public keys in directories at untrusted key servers. A directory is built using an authenticated binary prefix tree, offering similar properties as our hash treap. In CONIKS, user identities are presumably easy to brute-force, so they go further than Balloon in providing event privacy in proofs by using verifiable unpredictable functions and commitments to hide keys (identities) and values (user data). CONIKS stores every version of their (authenticated) data structure, introducing significant overhead compared to Balloon. On the other hand, CONIKS supports modifying and removing keys, similar to a PAD. Towards consistency, CONIKS additionally links snapshots together into a snapshot chain, together with a specified gossiping mechanism that greatly increases the probability that an attacker creating inconsistent snapshots is caught. This reduces the reliance on perfect gossiping, and could be used in Balloon. If the author ever wants to create a fork of snapshots for a subset of clients and monitors, it needs to maintain this fork forever for this subset or risk detection. Like CONIKS, we do not prevent an adversary compromising a server, or author, or both, from performing attacks: we provide means of detection after the fact.
9 Conclusions
This paper presented Balloon, an authenticated data structure composed of a history tree and a hash treap, that is tailored for privacy-preserving transparency logging. Balloon is a provably secure authenticated data structure, using a similar approach as Papamanthou et al. [19], under the modest assumption of a collision-resistant hash function. Balloon also supports efficiently verifiable inserts of new events and publicly verifiable consistency. Verifiable inserts enable the author to discard its copy of the (authenticated) data structure, only keeping constant storage, at the cost of transmitting and verifying proofs of a pruned version of the authenticated data structure. Publicly verifiable consistency enables anyone to verify the consistency of snapshots, laying the foundation for a forward-secure author, under the additional assumption of a perfect gossiping mechanism of snapshots. Balloon is practical, as shown in Sect. 7, and a more efficient solution in our setting than using a PAD, as summarised by Table 2.
Notes
- 1.
A commitment \(c_i\) is the root of the history tree for the i:th event, signed by the system. For the purpose of this paper, we omit the signature from the commitments.
- 2.
The priority can safely be discarded since it is derived solely from the key and implicit in the structure of the treap.
- 3.
\(queried[-1]\) denotes the index of the last inserted event in version queried of the authenticated data structure.
- 4.
Note that the signatures may differ since the signature scheme can be probabilistic.
- 5.
golang.org, accessed 2015-04-10.
- 6.
References
Anagnostopoulos, A., Goodrich, M.T., Tamassia, R.: Persistent authenticated dictionaries and their applications. In: Davida, G.I., Frankel, Y. (eds.) ISC 2001. LNCS, vol. 2200, pp. 379–393. Springer, Heidelberg (2001)
Aragon, C.R., Seidel, R.: Randomized search trees. In: FOCS, pp. 540–545. IEEE Computer Society (1989)
Basin, D.A., Cremers, C.J.F., Kim, T.H., Perrig, A., Sasse, R., Szalachowski, P.: ARPKI: attack resilient public-key infrastructure. In: CCS. ACM (2014)
Bernstein, D.J., Duif, N., Lange, T., Schwabe, P., Yang, B.Y.: High-speed high-security signatures. J. Cryptographic Eng. 2(2), 77–89 (2012)
Blum, M., Evans, W.S., Gemmell, P., Kannan, S., Naor, M.: Checking the correctness of memories. Algorithmica 12(2/3), 225–244 (1994)
Crosby, S.A., Wallach, D.S.: Efficient data structures for tamper-evident logging. In: USENIX Security Symposium, pp. 317–334. USENIX (2009)
Crosby, S.A., Wallach, D.S.: Super-efficient aggregating history-independent persistent authenticated dictionaries. In: Backes, M., Ning, P. (eds.) ESORICS 2009. LNCS, vol. 5789, pp. 671–688. Springer, Heidelberg (2009)
Crosby, S.A., Wallach, D.S.: Authenticated dictionaries: Real-world costs and trade-offs. ACM Trans. Inf. Syst. Secur. 14(2), 17 (2011)
Crosby, S.A.: Efficient tamper-evident data structures for untrusted servers. Ph.D. thesis, Rice University (2010)
Kim, T.H., Huang, L., Perrig, A., Jackson, C., Gligor, V.D.: Accountable key infrastructure (AKI): a proposal for a public-key validation infrastructure. In: World Wide Web Conference, pp. 679–690. ACM (2013)
Laurie, B., Kasper, E.: Revocation transparency (2012). http://www.links.org/files/RevocationTransparency.pdf
Laurie, B., Langley, A., Kasper, E.: Certificate Transparency. RFC 6962 (2013). http://tools.ietf.org/html/rfc6962
Ma, D., Tsudik, G.: Extended abstract: Forward-secure sequential aggregate authentication. In: IEEE Symposium on Security and Privacy, pp. 86–91. IEEE Computer Society (2007)
Melara, M.S., Blankstein, A., Bonneau, J., Freedman, M.J., Felten, E.W.: CONIKS: A privacy-preserving consistent key service for secure end-to-end communication. Cryptology ePrint Archive, Report 2014/1004 (2014). https://eprint.iacr.org/2014/1004
Merkle, R.C.: A digital signature based on a conventional encryption function. In: Pomerance, C. (ed.) CRYPTO 1987. LNCS, vol. 293, pp. 369–378. Springer, Heidelberg (1988)
Merkle, R.C.: A certified digital signature. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 218–238. Springer, Heidelberg (1990)
Miller, A., Hicks, M., Katz, J., Shi, E.: Authenticated data structures, generically. In: POPL, pp. 411–424. ACM (2014)
Nissim, K., Naor, M.: Certificate revocation and certificate update. In: USENIX, pp. 561–570. USENIX (1998)
Papamanthou, C., Tamassia, R., Triandopoulos, N.: Optimal verification of operations on dynamic sets. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 91–110. Springer, Heidelberg (2011)
Pulls, T., Peeters, R.: Balloon: A forward-secure append-only persistent authenticated data structure. Cryptology ePrint Archive, Report 2015/007 (2015). https://eprint.iacr.org/2015/007
Pulls, T., Peeters, R., Wouters, K.: Distributed privacy-preserving transparency logging. In: WPES, pp. 83–94. ACM (2013)
Ryan, M.D.: Enhanced certificate transparency and end-to-end encrypted mail. In: NDSS. The Internet Society (2014)
Schneier, B., Kelsey, J.: Secure audit logs to support computer forensics. ACM Trans. Inf. Syst. Secur. 2(2), 159–176 (1999)
Tamassia, R.: Authenticated data structures. In: Di Battista, G., Zwick, U. (eds.) ESA 2003. LNCS, vol. 2832, pp. 2–5. Springer, Heidelberg (2003)
Vliegen, J., Wouters, K., Grahn, C., Pulls, T.: Hardware strengthening a distributed logging scheme. In: DSD, pp. 171–176. IEEE (2012)
Yavuz, A.A., Ning, P., Reiter, M.K.: BAF and FI-BAF: efficient and publicly verifiable cryptographic schemes for secure logging in resource-constrained systems. ACM Trans. Inf. Syst. Secur. 15(2), 9 (2012)
Yu, J., Cheval, V., Ryan, M.: DTKI: a new formalized PKI with no trusted parties. CoRR abs/1408.1023 (2014). http://arxiv.org/abs/1408.1023
Acknowledgements
We would like to thank Simone Fischer-Hübner, Stefan Lindskog, Leonardo Martucci, Jenni Reuben, Philipp Winter, and Jiangshan Yu for their valuable feedback. Tobias Pulls has received funding from the Seventh Framework Programme for Research of the European Community under grant agreement no. 317550. This work was supported in part by the Research Council KU Leuven: GOA TENSE (GOA/11/007).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Proof of Security
Theorem 2
Balloon {genkey,setup,update,refresh,query,verify} is a secure ADS scheme for a data structure D, that contains a list of sets of events, according to Definition 3, assuming the collision-resistance of the underlying hash function.
Proof
The adversary initially outputs the authenticated data structure \({\mathtt{auth}(D_{0})}\) and the snapshot \(\mathsf{s}_0\) through an oracle call to algorithm setup. The adversary picks a polynomial number \(i=0,\dots ,h\) of updates with \(u_i\) insertions of unique events and outputs the data structure \(D_i\), the authenticated data structure \({\mathtt{auth}(D_{i})}\), and the snapshot \(\mathsf{s}_i\) through oracle access to update. Then it picks a query \(q =\) “a membership query for an event with key \(k \in \{0,1\}^{|{\mathtt{Hash}}(\cdot )|}\) in the data structure that is fixed by \(\mathsf{s}_{j}\), with \(0 \le j \le h+1\)”, a proof \(\varPi (q)\), and an answer \(\alpha (q)\) which is rejected by check \((q,\alpha (q),D_j)\) as incorrect. An adversary breaks security if verify \((q,\alpha (q),\varPi (q),\mathsf{s}_j,\mathtt{pk})\) outputs accept with non-negligible probability.
Assume a probabilistic polynomial time adversary \(\mathbf {Adv}\) that breaks security with non-negligible probability. Given that the different versions of the authenticated data structure and corresponding snapshots are generated through oracle access, these are correct, i.e., the authenticated data structure contains all elements of the data structure for each version, the root and commitment in each snapshot correspond to that version of the ADS and the signature in each snapshot verifies.
The tuple \((q,\alpha (q),D_j)\) is rejected by check in only three cases:
-
Case 1. \(\alpha (q)\) = false and there exists an event with key k in \(D_j\);
-
Case 2. \(\alpha \)(q) = {true, e} and there does not exists an event with key k in \(D_j\);
-
Case 3. \(\alpha \)(q) = {true, e} and the event \(e^*\) with key k in \(D_j\) differs from e: \(e = (k,v) \ne e^* = (k,v^*)\) or more specifically \(v \ne v^*\);
For all three cases where the check algorithm outputs reject, \(\mathbf {Adv}\) has to forge an authenticated path in the hash treap and/or history tree in order to get the verify algorithm to output accept:
-
Case 1. In the hash treap that is fixed by \(\mathsf{s}_{h+1}\), there is a node with key \(k' = {\mathtt{Hash}}(k)\) and the value \(v'\le j[-1]\). However for the verify algorithm to output accept for \(\alpha (q)\) = false, the authenticated path in the hash treap must go to either no node with key \(k'\) or a node with key \(k'\) for which the value \(v'\) is greater than the index of the last inserted event in the history tree that is fixed by \(\mathsf{s}_j\): \(v' > j[-1]\).
-
Case 2. In the hash treap that is fixed by \(\mathsf{s}_{h+1}\), there is either no node with key \(k' = {\mathtt{Hash}}(k)\) or a node with key \(k'\) for which the value \(v'\) is greater than the index of the last inserted event in the history tree that is fixed by \(\mathsf{s}_j\): \(v' > j[-1]\). However for the verify algorithm to output accept for \(\alpha \)(q) = {true, e}, the authenticated path in the hash treap must go to a node with key \(k'\), where the value \(v'\le j[-1]\). Note that, in this case, \(\mathcal {A}\) also needs to forge an authenticated path in the history tree to succeed.
-
Case 3. In the hash treap that is fixed by \(\mathsf{s}_{h+1}\), there is a leaf with key \(k' = {\mathtt{Hash}}(k)\) and the value \(v' \le j[-1]\). In the history tree, the leaf with key \(v'\) has the value \({\mathtt{Hash}}(e^*)\). However for the verify algorithm to output accept for \(\alpha \)(q)={true, e}, the authenticated path in the hash treap must go to a leaf with key \(k'\), where the value \(v'\le j[-1]\), for which the authenticated path in the history tree must go to a leaf with key \(v'\) and the value \({\mathtt{Hash}}(e)\).
From Lemma 1 it follows that we can construct a probabilistic polynomial time adversary \(\mathbf {Adv^*}\), by using \(\mathbf {Adv}\), that outputs a collision of the underlying hash function with non-negligible probability. \(\square \)
B Negative Result on Probabilistic Consistency
Probabilistic proofs are compelling, because they may enable more resource-constrained clients en-mass to verify consistency, removing the need for monitors that perform the relatively expensive role of downloading all events at a server. Assume the following pair of algorithms:
-
\(P \; {\leftarrow }\; \) B.IncGen \((\mathsf{s}_i, \mathsf{s}_j, \mathtt{rand})\): Generates a probabilistic incremental proof P using randomness \(\mathtt{rand}\) between \(\mathsf{s}_i\) and \(\mathsf{s}_j\), where \(i \le j\), from the Balloon B. Outputs P.
-
{\(\mathtt{accept}, \mathtt{reject}\)} \({\leftarrow }\) P.IncVerify \((\mathsf{s}_i, \mathsf{s}_j, \mathtt{rand})\): Verifies that P probabilistically proves that \(\mathsf{s}_j\) fixes every event fixed by \(s_i\), where \(i \le j\), using randomness \(\mathtt{rand}\).
1.1 B.1 Our Attempt
Our envisioned B.IncGen algorithm shows consistency in two steps. First, it uses the H.IncGen algorithm from the history tree. This ensures that the snapshots are consistent for the history tree. Second, it selects deterministically and uniformly at random based on \(\mathtt{rand}\) a number of events \(E =\,\, <e_j>\) from the history tree. Which events to select from depend on the two snapshots. For each selected event, the algorithm performs a query (Membership) for the event key \(k_j \; {\leftarrow }\; \mathtt{key}(e_j)\) to show that the event is part of the hash treap and points to the index of the event in the history tree.
The P.IncVerify algorithm checks the incremental proof in the history tree, verify (Membership)  accept for each output of query (Membership), and that the events E were selected correctly based on \(\mathtt{rand}\). Next, we explain an attack, why it works, and lessons learnt.
accept for each output of query (Membership), and that the events E were selected correctly based on \(\mathtt{rand}\). Next, we explain an attack, why it works, and lessons learnt.
1.2 B.2 Attack
The following attack allows an attacker to hide an arbitrary event that was inserted before author compromise. The attacker takes control over both the author and server just after snapshot \(s_t\). Assume that the attacker wants to remove an event \(e_j\) from Balloon, where \(j \le t[-1]\). The attacker does the following:
-
1.
Remove the event key \(k_j' = {\mathtt{Hash}}(k_j)\), where \(k_j \; {\leftarrow }\; \mathtt{key}(e_j)\), from the hash treap, insert a random key, and rebalance the treap if needed. This results is a modified ADS \({\mathtt{auth}(D_{t})}^*\).
-
2.
Generate a set of new events u and update the data structure: \(\mathtt{update}(u, D_t,\) \( {\mathtt{auth}(D_{t})}^*, \mathsf{s}_t, \mathtt{sk},\) \(\mathtt{pk})\), resulting in a new snapshot \(\mathsf{s}_{t+1}\).
It is clear that the snapshot \(\mathsf{s}_{t+1}\) is inconsistent with all other prior snapshots, \(\mathsf{s}_p\), where \(p \le t\).
Now, we show how the attacker can avoid being detected by P.IncVerify in the case that the verifier challenges the server (and therefore the attacker) to probabilistically prove the consistency between \(\mathsf{s}_p\) and \(\mathsf{s}_{t+1}\), AND that the randomness \(\mathtt{rand}\) provided by the verifier selects the event \(e_j\) that was modified by the attacker. The attacker can provide a valid incremental proof in the history tree, using H.IncGen, since the history tree has not been modified. However, the attacker cannot create a valid membership proof for an event with key \(k_j \; {\leftarrow }\; \mathtt{key}(e_j)\) in the ADS, since the key \(k_j' = {\mathtt{Hash}}(k_j)\) was removed from the hash treap in \({\mathtt{auth}(D_{t+1})}\). To avoid detection, the attacker puts back the event key \(k_j'\) in the hash treap and rebalances the treap if needed. By inserting a set of events using update, a new snapshot \(\mathsf{s}_{t+2}\) is generated, which is then used to perform the membership query against that will now output a valid membership proof.
1.3 B.3 Lessons Learnt
This attack succeeds because the attacker can, once having compromised the author and server, (a) create snapshots at will; and (b) membership queries are always performed on the current version of the hash treap.
In settings where snapshots are generated periodically, e.g., once a day, the probability of the attacker getting caught in this way is non-negligible given a sufficient number of queries. However, as long as the attacker can create snapshots at will, the probability that it will be detected with probabilistic incremental proofs is zero, as long as it cannot be challenged to generate past versions of the hash treap; and there are no monitors or another mechanism, that prevent the attacker from modifying or deleting events that were inserted into the ADS prior to compromise.
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Pulls, T., Peeters, R. (2015). Balloon: A Forward-Secure Append-Only Persistent Authenticated Data Structure. In: Pernul, G., Y A Ryan, P., Weippl, E. (eds) Computer Security -- ESORICS 2015. ESORICS 2015. Lecture Notes in Computer Science(), vol 9327. Springer, Cham. https://doi.org/10.1007/978-3-319-24177-7_31
Download citation
DOI: https://doi.org/10.1007/978-3-319-24177-7_31
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-24176-0
Online ISBN: 978-3-319-24177-7
eBook Packages: Computer ScienceComputer Science (R0)


 or otherwise a member. Verification checks that
or otherwise a member. Verification checks that 

 ;
;

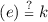
 ,
,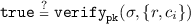 ; and
; and ; and
; and .
.