Abstract
Message authentication code, MAC for short, is a symmetric-key cryptographic function for authenticity. A standard MAC verification only tells whether the message is valid or invalid, and thus we can not identify which part is corrupted in case of invalid message. In this paper we study a class of MAC functions that enables to identify the part of corruption, which we call group testing MAC (GTM). This can be seen as an application of a classical (non-adaptive) combinatorial group testing to MAC. Although the basic concept of GTM (or its keyless variant) has been proposed in various application areas, such as data forensics and computer virus testing, they rather treat the underlying MAC function as a black box, and exact computation cost for GTM seems to be overlooked. In this paper, we study the computational aspect of GTM, and show that a simple yet non-trivial extension of parallelizable MAC (PMAC) enables \(O(m+t)\) computation for m data items and t tests, irrespective of the underlying test matrix we use, under a natural security model. This greatly improves efficiency from naively applying a black-box MAC for each test, which requires O(mt) time. Based on existing group testing methods, we also present experimental results of our proposal and observe that ours runs as fast as taking single MAC tag, with speed-up from the conventional method by factor around 8 to 15 for \(m=10^4\) to \(10^5\) items.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Message authentication code (MAC) is a symmetric-key cryptographic function for authenticity. A MAC function, F, takes a secret key K and a message M to produce a tag \(T=F(K,M)\). A legitimate user with key K first takes (M, T) and later verifies the validity of a tuple \((M',T')\), which may be corrupted from (M, T), by computing \(T''=F(K,M')\) and checking if \(T''=T'\) holds or not. While MAC-based integrity check is simple and efficient, if verification fails one can not obtain any further information on what part of message is corrupted. On the other extreme side, by partitioning data into m items, say 4K-byte sectors of HDD, and taking tags for each item, we can always identify all corrupted items. However this can be impractical due to a huge impact to the storage.
This tread-off between the number of tags and the information on corruption can be improved by taking multiple MAC tags for overlapping parts of data items. If we carefully choose overlapping parts it allows us to identify the corrupted items if they are few. This is an interesting application of combinatorial group testing (CGT) to message authentication, as pointed out by literatures in various applications areas. Here, CGT is a method to identify defectives from a large number of samples using group tests (see Du and Hwang [15] for a good summary). For example, Goodrich et al. [20] proposed a MAC scheme combined with CGT for data forensics applications. Crescenzo et al. [11] proposed a MAC scheme for corruption localization not only restricted to identification. For schemes other than MAC, Crescenzo, Jiang and Safavi-Naini proposed corruption-localizing hash schemes [12] and it was further improved and extended at [8, 10] incorporating the theory of CGT. We can find various applications such as computer virus testing [13] and HDD integrity check [17]. Relationship between CGT and signature batch verification was studied by Zaverucha and Stinson [30].
CGT has been extensively studied from the viewpoints of combinatorics and coding theory. In particular, non-adaptive CGT (NCGT) using t tests for m items is specified by a \(t\times m\) binary test matrix, and there are numerous results on the efficient matrix constructions with primary focus on the number of tests (rows), both deterministic and randomized, see e.g. Du and Hwang [15] and Ngo and Du [24]. In application of NCGT to MAC, we first choose a test matrix and then take MAC tags following the chosen test matrix. We call such combined MAC scheme group testing MAC (GTM). GTM can in principle use any of known test matrix designs. In this paper, we study the computational cost of GTM. This has not been deeply explored by previous researches as they assume MAC function as a black box. Naturally we need to compute t MAC tags for distinct parts of m items, and standard MAC needs O(m) time for computing a tag for m items (assuming constant item length). Hence the computation cost is O(w) where w is the weight of test matrix, which is at most O(mt). In practice GTM requires many overlapping items between distinct tests to have good ability in corruption identification, thus the computation cost is quite higher than taking single tag for all items as long as MAC function is used as a black box. In this paper, we show that a special form of MAC enables to reduce the computation cost of GTM to \(O(m+t)\) for any matrix of t tests and m items. The crux of our proposal is the introduction of a parallelizable MAC defined over a vector space which efficiently handles empty string (bit string of length zero) without computation. This is a simple yet non-trivial extension of a parallelizable blockcipher-based MAC called PMAC [7, 26]. Additionally our scheme also enables efficient incremental update of data items in the same manner to PMAC, and even the update of test matrix. To analyze the security of our proposal we consider several formal security notions, and show that our scheme is secure with respect to them, in a concrete provable security framework proposed by Bellare et al. [3]. Our notions are rather straightforward extension of those for deterministic MAC [5, 6], and have some similarities with those seen in [12, 20].
We also present experimental implementation of our scheme, using existing NCGT matrix constructions and AES blockcipher. We show that our scheme achieves essentially the same speed as the single tag computation, which is the speed of AES itself if each item is sufficiently long. The factor of speed-up compared to the conventional scheme is dependent on the matrix, and in our experiments it is expected to be around 8 to 15 for \(10^4\) to \(10^5\) items. The implementation results show that differences from theory and practice are quite small.
2 Preliminaries
Let \(\{0,1\}^\bullet \) be the set of all binary strings, including the empty string \(\varepsilon \). We write the bit length of \(X\in \{0,1\}^{\bullet }\) by |X|. Here \(|\varepsilon |=0\). We define \(\{0,1\}^*\mathop {=}\limits ^{{{\tiny \mathrm{def}}}}\{0,1\}^{\bullet }\setminus \varepsilon \). We define a vector space consisting of m non-empty strings as \(\{0,1\}^{*m}\mathop {=}\limits ^{{{\tiny \mathrm{def}}}}(\{0,1\}^*)^m\). Similarly let \(\{0,1\}^{\bullet m}\mathop {=}\limits ^{{{\tiny \mathrm{def}}}}(\{0,1\}^\bullet )^m\) as a vector space consisting of m possibly empty strings, which we call extended vector space. Here note that \((\varepsilon ,v)\) and \((v,\varepsilon )\) for \(v\ne \varepsilon \) are distinct elements of \(\{0,1\}^{\bullet 2}\). Let \(M=(M[1],\dots ,M[m])\) and \(M'=(M'[1],\dots ,M'[m])\) be vectors of m strings in \(\{0,1\}^{*m}\). We define \(\mathsf {diff}(M,M')=\{i: M[i]\ne M'[i]\}\) and \({\varDelta }(M,M')=(Y[1],\dots ,Y[m])\) where \(Y[i]=1\) if \(M[i]\ne M'[i]\) and otherwise \(Y[i]=0\). Let \(x\odot 1= x\) and \(x\odot 0= \varepsilon \) for any \(x\in \{0,1\}^*\), and for \(B=(B[1],\dots ,B[m])\in \{0,1\}^m\), we let \(M\odot B=(M[1]\odot B[1], \dots , M[m]\odot B[m])\in \{0,1\}^{\bullet m}\). Moreover, let \(M\ominus B\in \{0,1\}^{*m}\) be a vector obtained by removing all empty strings from \(M\odot B\). For example if \(M=(M[1],M[2],M[3],M[4])\) and \(B=(1,0,1,0)\) we have \(M\odot B=(M[1],\varepsilon ,M[3],\varepsilon )\) and \(M\ominus B=(M[1],M[3])\).
For \(n\times m\) binary matrix \(\mathbb {M}\), \(\mathbb {M}_i\) denotes the i-the row, \(\mathbb {M}_{i,j}\) denotes the entry at i-th row and j-th column. We let \(\mathcal{I}(\mathbb {M}_i) \mathop {=}\limits ^{{{\tiny \mathrm{def}}}}\{j: \mathbb {M}_{i,j}=1\}\). We also let \({\text{ Hw }}(\mathbb {M})=\sum _{i}|\mathcal{I}(\mathbb {M}_i)|\) to denote the hamming weight of \(\mathbb {M}\).
Keyed Function and Random Function. For keyed function \(F:\mathcal{K}\times \mathcal{X}\rightarrow \mathcal{Y}\) with key \(K\in \mathcal{K}\), we may simply write \(F_K:\mathcal{X}\rightarrow \mathcal{Y}\) if key space is obvious, or even write as \(F:\mathcal{X}\rightarrow \mathcal{Y}\) if being keyed with K is obvious. If \(E_K:\mathcal{X}\rightarrow \mathcal{X}\) is a keyed permutation, or a blockcipher, \(E_K\) is a permutation over \(\mathcal{X}\) for every \(K\in \mathcal{K}\). Its inverse is denoted by \(E^{-1}_K\). A tweakable keyed permutation, also known as tweakable blockcipher (TBC) [23] is a family of keyed permutation (blockcipher) over \(\mathcal{X}\) indexed by a public parameter called tweak \(V\in \mathcal{V}\). It is written as \(\widetilde{E}_K:\mathcal{V}\times \mathcal{X}\rightarrow \mathcal{X}\). The encryption of TBC is written as \(C=\widetilde{E}_K^{V}(M)\) for plaintext M, tweak V and ciphertext C, and the decryption is written as \(M=\widetilde{E}_K^{-1, V}(C)\). For two keyed functions, \(F_K,F'_{K'}:\mathcal{X}\rightarrow \mathcal{Y}\), we say they are compatible, i.e. they have the same input and output domains. Here, the key spaces are not necessarily identical. Let \({\text{ Func }}(n,m)\) be the set of all functions \(\{0,1\}^{n}\rightarrow \{0,1\}^{m}\), and let \({\text{ Perm }}(n)\) be the set of all permutations over \(\{0,1\}^n\). A uniform random function (URF) having n-bit input and m-bit output is a function family uniformly distributed over \({\text{ Func }}(n,m)\). We write \(X\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathcal{X}\) to denote the uniform sampling of X over \(\mathcal{X}\). Then a URF is expressed as \({\mathsf{R}}\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}{\text{ Func }}(n,m)\). A uniform random permutation (URP) over n-bit space is similarly denoted by \({\mathsf{P}}\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}{\text{ Perm }}(n)\). We also define tweakable URP. Let \(\mathcal{V}\) be a set of tweak and \({\text{ Perm }}^\mathcal{V}(n)\) be the set of all functions \(\mathcal{V}\times \{0,1\}^n\rightarrow \{0,1\}^n\) such that, for any \(f\in {\text{ Perm }}^\mathcal{V}(n)\) and \(v\in \mathcal{V}\), \(f(v,*)\) is a permutation. A tweakable n-bit URP with tweak \(V\in \mathcal{V}\) is denoted by \(\widetilde{{\mathsf{P}}}\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}{\text{ Perm }}^\mathcal{V}(n)\). In addition, a URF \({\mathsf{R}}:\mathcal{V}\times \mathcal{X}\rightarrow \mathcal{Y}\) is also called a tweakable URF when \(V\in \mathcal{V}\) is used as a tweak in the application we discuss, and we also write it as \(\widetilde{{\mathsf{R}}}:\mathcal{V}\times \mathcal{X}\rightarrow \mathcal{Y}\).
Pseudorandom Function. For c oracles, \(O_1,O_2,\dots ,O_c\), \({\mathcal {A}}^{O_1,O_2,\dots ,O_c}\) denotes the adversary \({\mathcal {A}}\) querying these c oracles. Let \(F_K,G_{K'}:\mathcal{X}\rightarrow \mathcal{Y}\) be two compatible keyed functions, and let \({\mathcal {A}}\) be an adversary trying to distinguish them using queries with 1-bit final output. Then the (chosen-plaintext attack, CPA) advantage of \({\mathcal {A}}\) is defined as

where \({\mathcal {A}}^{F_K}\Rightarrow 1\) denotes the event that \({\mathcal {A}}\)’s final output is 1 after queries to \(F_K\). The probability is defined over a uniform sampling of K and internal randomness of \({\mathcal {A}}\). If F and G are tweakable, a tweak in a query is arbitrarily chosen by the adversary. Using URF \({\mathsf{R}}\) compatible with \(F_K\), we define
In a similar manner, using URP \({\mathsf{P}}\) compatible with a keyed permutation \(E_K\) we define \( {\texttt {Adv}}^{ {\texttt {prp}}}_{E_K}({\mathcal {A}})\mathop {=}\limits ^{{{\tiny \mathrm{def}}}} {\texttt {Adv}}^{ {\texttt {cpa}}}_{E_K,{\mathsf{P}}}({\mathcal {A}})\). For tweakable keyed permutation \(\widetilde{E}_K\), we also define \( {\texttt {Adv}}^{ {\texttt {tprp}}}_{\widetilde{E}_K}({\mathcal {A}})\mathop {=}\limits ^{{{\tiny \mathrm{def}}}} {\texttt {Adv}}^{ {\texttt {cpa}}}_{\widetilde{E}_K,\widetilde{{\mathsf{P}}}}({\mathcal {A}})\), where \(\widetilde{{\mathsf{P}}}\) is a tweakable URP compatible with \(\widetilde{E}_K\).
If adversary \({\mathcal {A}}\) is with time complexity, it means the total computation time and memory of \({\mathcal {A}}\) required for query generation and final decision, in some fixed model. If there is no description on time complexity of \({\mathcal {A}}\), it means \({\mathcal {A}}\) has no computational restriction. Conventionally we say \(F_K\) is a pseudorandom function (PRF) if \( {\texttt {Adv}}^{ {\texttt {cpa}}}_{F_K}({\mathcal {A}})\) is negligible for all practical adversaries (though the formal definition [19] requires \(F_K\) to be a function family). Similarly we say \(F_K\) is a pseudorandom permutation (PRP) if \( {\texttt {Adv}}^{ {\texttt {prp}}}_{F_K}({\mathcal {A}})\) is negligible and \(F_K\) is invertible. Tweakable PRP (TPRP) is similarly defined with \( {\texttt {Adv}}^{ {\texttt {tprp}}}_{\widetilde{E}_K}({\mathcal {A}})\). We also introduce the notion of tweakable PRF, which is essentially a PRF containing tweak space as a part of input.
3 MAC for Corruption Identification
3.1 Combinatorial Group Testing
We start with a brief introduction of CGT and its application to MAC. CGT was originally formulated by Dorfman [14] for medical testing of blood supplies during World War II. Formally, let us assume that we have a set of m items, \({\mathbf M}=\{M[1],\dots ,M[m]\}\), and each item is either normal or defective. The goal is to identify the defective items among \({\mathbf M}\) using group testing, that is, we choose a subset \({\mathbf S}\subset {\mathbf M}\) and query if \({\mathbf S}\) contains at least one defective item. A response to a query is said to be positive if it indicates the existence of at least one defective, and otherwise said to be negative. We usually assume a prior knowledge or assumption about the maximum number of possible defective items, and the central question of CGT is how to form effective tests to identify all defective items. If each query is not depending on responses of other queries, the scheme is called non-adaptive CGT (NCGT), which is specified by a \(t\times m\) binary test matrix \(\mathbb {Q}\). Here, t denotes the number of tests and \(\mathbb {Q}_{i,j}=1\) denotes that M[j] is included in the i-th test. The construction of test matrix is deeply related to the combinatorics and coding theory and there are numerous studies on the construction of test matrix. See Du and Hwang [15] for a collection of these results. It is known that we need \(t=O(d^2\log m)\) non-adaptive tests to identify all defective items if there are at most d defective items, hence we can greatly reduce the number of tags from naively taking m tags. When \(d=1\) there is a simple Hamming code based matrix achieving \(t=\lceil \log m\rceil \). For \(d>1\) deterministic construction achieving \(\Theta (d^2\log m)\) is known [25], however, finding a construction achieving the minimum number of tests (not asymptotically) is generally not easy and remains as a vital research topic.
A conventional approach to GTM is as follows, which is also seen in the previous studies [11, 20]. For m data items represented as a vector \(M=(M[1],\dots ,M[m])\in \{0,1\}^{*m}\), we first prepare a conventional MAC function defined over input space of \(\{0,1\}^*\) (or \(\{0,1\}^\bullet \)), say HMAC, and using it with an appropriate input encoding, we build a MAC function for vector space \({\text{ MAC }}_K:\{0,1\}^{*m}\rightarrow \{0,1\}^n\). We also prepare a \(t\times m\) test matrix \(\mathbb {Q}\). Then for each \(\mathbb {Q}_i\) we compute
to obtain the legitimate MAC tag vector, \(T=(T[1],\dots ,T[t])\). Later, given potentially corrupted items, \(M'=(M'[1],\dots ,M'[m])\), and T, we compute \(T'=(T'[1],\dots ,T'[t])\) where \(T'[i] = {\text{ MAC }}_K(M'\ominus \mathbb {Q}_i)\), and compare T and \(T'\), obtain \(Z={\varDelta }(T, T')\). From the property of \(\mathbb {Q}\), if \(0\le |\mathsf {diff}(M,M')|\le d\) holds true Z is uniquely mapped to \({\varDelta }(M,M')\), i.e. the indexes of all corrupted items. This procedure is also called decoding in the field of CGT. It is possible to prove that producing \(T'\) such that Z does not correctly indicate \({\varDelta }(M,M')\) implies a successful forgery against \({\text{ MAC }}_K\) (See Sect. 3.6).
As mentioned there are plenty of efficient construction methods for \(\mathbb {Q}\) from the literature, deterministic or random, with various additional properties, and we can basically adopt any of them with any MAC. What we here ask is the computation cost given \(\mathbb {Q}\). Defining the unit of computation as an internal operation of MAC to process each item, e.g. the compression function of HMAC-SHA2, the conventional approach described above, taking MAC as a black box, generally requires \(O({\text{ Hw }}(\mathbb {Q}))\le O(mt)\) computation, which can be significantly larger than O(m), the time for taking one MAC tag for M. Once given \(\mathbb {Q}\) and \({\text{ MAC }}_K\) it is possible to find some optimizations, however this will be cumbersome as we need ad-hoc optimization for each \(\mathbb {Q}\). In the following, we show that a simple parallelizable MAC enables to reduce the computation cost to \(O(m+t)\) for any \(\mathbb {Q}\) with t rows. Usually m is much greater than t thus our result implies that GTM can run mostly as fast as single MAC computation.
3.2 MAC for Extended Vector Space
Let \(\mathcal{V}\) and \(\mathcal{V}'\) be sets of integers used as tweak spaces. Let \(\overline{F}_K:\mathcal{V}\times \{0,1\}^*\rightarrow \{0,1\}^n\) be a keyed function and let \(F_K:\mathcal{V}\times \{0,1\}^\bullet \rightarrow \{0,1\}^n\) be defined as \(F_K(i,x) =\overline{F}_K(i,x)\) if \(x\ne \varepsilon \) and \(F_K(i,x)=0^n\) otherwise, for any \(i\in \mathcal{V}\). Let \(G_{K'}:\mathcal{V}'\times \{0,1\}^n\rightarrow \{0,1\}^n\) be a tweakable keyed permutation over n bits. We may write \(F^i_K(x)\) and \(G^j_{K'}(z)\) to denote \(F_K(i,x)\) and \(G_{K'}(j,z)\).
Let \(\mathsf {gtm}[F_K,G_{K'}]\) be a MAC function which takes an extended vector \(X\in \{0,1\}^{\bullet m}\) for fixed m and outputs an n-bit tag with tweak \(h\in \mathcal{V}'\), defined as
For example, if \(m\!=\!3\) and \(a,b\in \{0,1\}^*\), \(\mathsf {gtm}[F_K,G_{K'}](h,(a,\varepsilon ,b))\!=\!~G^{h}_{K'}(F^1_K(a)\oplus F^3_K(b))\) holds. Assuming \(|X[i]|\le n\) for all \(i\le m\) and the use of n-bit blockcipher \(E_K\) for instantiations of F and G, \(\mathsf {gtm}\) is similar to parallelizable blockcipher-based MAC called PMAC [7, 26]. However, we observe important differences that in PMAC the input X is in \(\{0,1\}^\bullet \) and we apply partitioning to X into n-bit blocks, and the last item X[m] is directly XORed to the state. Moreover, PMAC does not allow X[i] to be empty for any i,Footnote 1 thus to process \(X\in \{0,1\}^{\bullet m}\) with PMAC we need some encoding of X into \(\{0,1\}^\bullet \). In Sect. 3.6 we will prove that \(\mathsf {gtm}[F_K,G_{K'}]\) is a tweakable PRF\(:\mathcal{V}'\times \{0,1\}^{\bullet m}\rightarrow \{0,1\}^n\) if \(\overline{F}_K\) is a tweakable PRF with tweak space \(\mathcal{V}=\{1,\dots ,m\}\), and \(G_{K'}\) is an n-bit tweakable PRP with tweak space \(\mathcal{V}'\).
We stress that (2) is not secure if input space contains extended vectors of different number of strings (i.e. m can be changed). Indeed, if m could be changed we have the same outputs for \(X=(X[1])\) and \(X'=(X[1],\varepsilon )\). Such attack can be prevented by taking the number of component strings as a part of G’s tweak. We prefer (2) for its simplicity and the fact that \(\mathsf {gtm}\) for fixed m is enough to provide a secure GTM for any fixed-size, \(t\times m\) test matrix.
3.3 Efficient Group Testing MAC
Given a \(t\times m\) test matrix \(\mathbb {Q}\) and a list of m items denoted by \(M\in \{0,1\}^{*m}\), now what we want to compute is
Since any test that includes M[j] adds \(F^{j}_K(M[j])\) to its internal state, \(F^{j}_K(M[j])\) can be shared for all tests that include M[j]. In other words, the computation of (3) can be done by reading each M[j], computing \(F^{j}_K(M[j])\), and XORing to the state memory block for the i-th test (denoted by S[i]) for all i such that \(\mathbb {Q}_{i,j}=1\). Then we compute \(T[i]=G^i_{K'}(S[i])\) for all i. This requires m calls of F and t calls of G using t state memory blocks for any \(\mathbb {Q}\). Note that such computation can not be done by a black-box application of PMAC with input encoding (from \(\{0,1\}^{\bullet m}\) to \(\{0,1\}^\bullet \)).
We write this procedure as \(\mathsf {GTM}[F_K,G_{K'}].\text{ Tag }\), which uses \(\mathsf {gtm}\) as a subroutine but in a decomposed way described above. It is shown in Fig. 1. A simple procedure for the corruption identification, also known as naive decoder, is to apply \(\mathsf {GTM}[F_K,G_{K'}].\text{ Tag }\) for the (possibly corrupted) data items, and removes all data items which is included in a test with negative outcome, i.e. a test that correctly passed. The remaining items are considered to be corrupted. This procedure is defined as \(\mathsf {GTM}[F_K,G_{K'}].\text{ Ident }\). Moreover, we require that \(\mathsf {GTM}[F_K,G_{K'}]\) to work as an ordinal MAC for the whole data items or each subset specified by \(\mathbb {Q}_i\). The corresponding verification functions are defined as \(\mathsf {GTM}[F_K,G_{K'}].\text{ Verify }\) and \(\mathsf {GTM}[F_K,G_{K'}].\text{ Verify }^{(i)}\) shown in Fig. 1. The corresponding security notions will be described in Sect. 3.4.
In the definition of \(\mathsf {GTM}\) we assume \(M\in \{0,1\}^{*m}\), however extension to \(M\in \{0,1\}^{\bullet m}\) is trivially possible by additional input encoding for F.
Properties. We remark that \(\mathsf {gtm}[F_K,G_{K'}]\) is parallelizable. It also supports incremental update in the same manner to PMAC. For example, if we have \(T[i] = \mathsf {gtm}[F_K,G_{K'}](i,M\odot \mathbb {Q}_i)\) for some i and j with \(\mathbb {Q}_{i,j}=1\), re-computation of T[i] with incremental update of M[j] to \(M'[j]\ne M[j]\) requires two invocations of F and G, i.e., we apply \(G^{-1,i}_{K'}\) to T[i] and compute \(F_K^{j}(M[j])\oplus F_K^{j}(M'[j])\) to renew the state, and finally apply \(G^{i}_{K'}\) to the state to renew T[i]. This incremental update is useful when the data is large and frequently updated by items.
We also remark that even the incremental update of \(\mathbb {Q}\) (i.e. a change in the test matrix) is efficiently handled. For instance, if we want to change \(\mathbb {Q}_{i,j}=0\) to \(\mathbb {Q}_{i,j}=1\) then we add \(F_K^{j}(M[j])\) to \(G^{-1,i}_{K'}(T[i])\). However, we have not investigated the practical application of this functionality.
3.4 Security Notions
To consider the security of our proposal, we need formal security notions. Generally GTM can be considered as an extension of deterministic MAC, having input in \(\{0,1\}^{*m}\) and output in \((\{0,1\}^n)^t\) with a \(t\times m\) binary matrix \(\mathbb {Q}\) as a public parameter, equipped with corruption identification procedure in addition to tagging and verification procedures. Therefore we make our notions as natural extensions of those for deterministic MACs [5, 6]. We intend to define our notions so that they can be satisfied if item subset specified by a test (i.e. \(\{M[j]:\mathbb {Q}_{i,j}=1\}\)) is processed by a PRF, independent for each test, and the underlying \(\mathbb {Q}\) is appropriate for both MAC and corruption identification. We later show that \(\mathsf {GTM}[F_K,G_{K'}]\) is in fact secure with respect to our notions.
Let \(\mathbb {Q}\) be a \(t\times m\) binary matrix. Let \(\mathsf {MAC}_{\mathbf K}:\mathcal{M}\rightarrow \mathcal{T}\) with \(\mathcal{M}=\{0,1\}^{*m}\) and \(\mathcal{T}=(\{0,1\}^n)^t\) be a GTM scheme using test matrix \(\mathbb {Q}\). We also let \(\mathsf {MAC}_{\mathbf K}^{(i)}:\mathcal{M}\rightarrow \{0,1\}^n\) for \(i=1,\dots ,t\) to denote the corresponding MAC for the i-th test, that is, \(\mathsf {MAC}_{\mathbf K}(M) = (\mathsf {MAC}_{\mathbf K}^{(1)}(M),\dots ,\mathsf {MAC}_{\mathbf K}^{(t)}(M))\).
To define the security notions for \(\mathsf {MAC}\), we introduce several oracles.
Definition 1
Let \(M,M'\in \mathcal{M}=\{0,1\}^{*m}\) and \(T,T',\widehat{T}\in \mathcal{T}=(\{0,1\}^n)^t\). Let \(\mathsf {MAC}_{\mathbf K}.\mathrm{Tag}\) be tagging oracle which takes M and returns output as \(T=\mathsf {MAC}_{\mathbf K}(M)\). Let \(\mathsf {MAC}_{\mathbf K}.\mathrm{Verify}\) be the verification oracle which takes \((M',T')\in \mathcal{M}\times \mathcal{T}\) and evaluates \(\widehat{T}=\mathsf {MAC}_{\mathbf K}(M')\), and returns \(\top \) if \(T'=\widehat{T}\) (i.e. it is valid) and otherwise \(\bot \) (i.e. it is invalid). We define verification-i oracle \(\mathsf {MAC}_{\mathbf K}.\mathrm{Verify}^{(i)}\) which takes \((M',T'[i])\) to compute \(\widehat{T}[i] = \mathsf {MAC}_{\mathbf K}^{(i)}(M')\) and returns \(\top \) if \(\widehat{T}[i]=T'[i]\), and \(\bot \) otherwise. We also define identification oracle \(\mathsf {MAC}_{\mathbf K}. \mathrm{Ident}\) which takes \((M',T')\) and computes the index set of possibly corrupted items, simply obtained by evicting \(\mathcal{I}(\mathbb {Q}_i)\) from \(\{1,\dots ,m\}\) for all i such that i-th test is failed.
By setting \(\mathsf {MAC}_{\mathbf K}=\mathsf {GTM}[F_K,G_{K'}]\), these oracles are formally defined by Fig. 1.
We define the following three security notions. Let \(\mathcal {O}_{T}\), \(\mathcal {O}_{V}\), \(\mathcal {O}_{V}^{(i)}\), and \(\mathcal {O}_{I}\) respectively denote tagging, verification, verification-i, and identification oracles for \(\mathsf {MAC}_{\mathbf K}\). Here we fix the number of items, m, and \(t\times m\) test matrix \(\mathbb {Q}\).
-
1.
Tag vector forgery (TVF). Let \({\mathcal {A}}_1\) be the adversary who queries \((\mathcal {O}_{T},\mathcal {O}_{V})\). Suppose \({\mathcal {A}}_1\) obtains \((M_1,T_1),\dots ,(M_q,T_q)\) via q (adaptive, chosen-plaintext) queries to \(\mathcal {O}_{T}\) (where \((M_i,T_i)\in \{0,1\}^{*m}\times (\{0,1\}^n)^t\)) and then determines \((M',T')\in \{0,1\}^{*m}\times (\{0,1\}^n)^t\) as a query to \(\mathcal {O}_{V}\). We say \({\mathcal {A}}_1\) forges if \({\mathcal {A}}_1\) receives \(\top \) from \(\mathcal {O}_{V}\) and \((M',T')\ne (M_i,T_i)\) for all \(i=1,\dots ,q\). The advantage of \({\mathcal {A}}_1\) is defined as
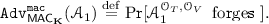 (4)
(4)We say \(\mathsf {MAC}_{\mathbf K}\) is secure against tag vector forgery if
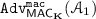 is negligibly small for all practical adversaries.
is negligibly small for all practical adversaries. -
2.
Tag string forgery (TSF). Fix \(i\in \{1,\dots ,t\}\). Let \({\mathcal {A}}_2\) be the adversary who queries \((\mathcal {O}_{T},\mathcal {O}_{V}^{(i)})\). Suppose \({\mathcal {A}}_2\) first obtains \((M_j,T_j)\) for \(j=1,\dots ,q\) via q queries to \(\mathcal {O}_{T}\), and then determines a query to \(\mathcal {O}_{V}^{(i)}\) as \((M',T'[i])\). We say \({\mathcal {A}}_2\) forges if \({\mathcal {A}}_2\) receives \(\top \) from \(\mathcal {O}_{V}^{(i)}\) and \((M'\ominus \mathbb {Q}_i,T'[i])\ne (M_j\ominus \mathbb {Q}_i,T_j[i])\) for all \(j=1,\dots ,q\). The advantage of \({\mathcal {A}}_2\) is defined as
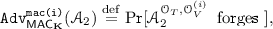 (5)
(5)and we say \(\mathsf {MAC}_{\mathbf K}\) is secure against tag string forgery if
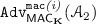 is negligibly small for all practical adversaries, for all \(i=1,\dots ,t\).
is negligibly small for all practical adversaries, for all \(i=1,\dots ,t\). -
3.
Corruption misidentification (CM). Let \({\mathcal {A}}_3\) be a d-corruptive adversary who first performs q distinct queries to \(\mathcal {O}_{T}\) and obtains \((M_1,T_1),\dots ,(M_q,T_q)\), and then queries \((M',T')\) to \(\mathcal {O}_{I}\) such that \(T'=T_i\) for some i and \(1\le |\mathsf {diff}(M',M_i)|\le d\). We say \({\mathcal {A}}_3\) forges if (1) we have \(T_i=T_j\) for some \(i\ne j\) or (2) all \(T_i\)s are unique and \(\mathcal {O}_{I}\) returns \(\mathcal{P}\subseteq \{1,\dots ,m\}\) such that \(\mathcal{P}\ne \mathsf {diff}(M',M_i)\) (where index i is uniquely determined from \(T'\)). We define
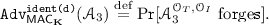 (6)
(6)For some fixed d, we say \(\mathsf {MAC}_{\mathbf K}\) is secure against corruption misidentification if
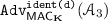 is negligibly small for all practical d-corrupting adversaries.
is negligibly small for all practical d-corrupting adversaries.
We will call these notions as TVF, TSF, and CM-security respectively. Note that in CM-security we safely let the adversary win if it finds a tag vector collision while querying \(\mathcal {O}_{T}\). Finally we say \(\mathsf {MAC}_{\mathbf K}\) is secure if it is secure with respect to all three notions.
Requirements on Test Matrix. To fulfill all of our security notions, test matrix \(\mathbb {Q}\) needs to satisfy some conditions. We naturally assume that all rows of \(\mathbb {Q}\) are unique. In the standard scenario of NCGT, it is known that \(\mathbb {Q}\) should be at least d-separableFootnote 2, that is, unions (bitwise logical OR) of up to d columns of \(\mathbb {Q}\) are all distinct. Here a union can include no column of \(\mathbb {Q}\) which is all-zero vector, and thus \(\mathbb {Q}\) cannot have all-zero column. A stronger definition is d-disjunct which means that any union of up to d columns does not contain a column of \(\mathbb {Q}\). This notion is useful in practice since if \(\mathbb {Q}\) is d-disjunct, correct decoding (corruption identification in our case) is always possible by naive decoder mentioned earlier which simply evicts all items used in at least one test that was negative. Moreover, we could always detect the existence of more than d defective items. See e.g. [15, 16, 24] for more details. Following these observations we set \(\mathsf {GTM}[F_K,G_{K'}].\text{ Ident }\) as naive decoder and require \(\mathbb {Q}\) to be d-disjunct for CM-security with d-corrupting adversaries. The existence of all-zero column also immediately implies a trivial attack against TVF-security.
TSF-security is independent of \(\mathbb {Q}\) because \(\mathbb {Q}_i\) specifies the input space of \(\mathsf {MAC}^{(i)}_{\mathbf K}\), and if \(\mathsf {MAC}^{(i)}_{\mathbf K}\) is an independent, secure MAC for each i, TSF-security is trivially satisfied for any \(\mathbb {Q}\).
For TVF-security, however, we require that \(\mathbb {Q}\) contains an all-one row, which shows a separation between TSF and TVF-securities.
Proposition 1
For any GTM using \(t\times m\) test matrix \(\mathbb {Q}\), if \(\mathbb {Q}\) does not contain an all-one row, TVF-security can be broken using at most \(t+1\) queries.
Proof
Let us assume \(\mathbb {Q}\) has no all-one row. Let a and b be two distinct non-empty strings. Then, for each \(i=1,\dots ,t\) the adversary queries \(M_i=(M_i[1],\dots ,M_i[m])\) to the tagging oracle, where \(M_i[j] = a\) if \(\mathbb {Q}_{i,j}=1\) and \(M_i[j] = b\) if \(\mathbb {Q}_{i,j}=0\), and receives \(T_i=(T_i[1],\dots ,T_i[t])\). Then the adversary queries \((M',T')\) to the verification oracle, where \(M'=(a,\dots ,a)\) and \(T'[j]=T_j[j]\). This query is always accepted. \(\quad \square \)
Consequently we require the following.
Definition 2
We say \(t\times m\) test matrix \(\mathbb {Q}\) is sound for d-corruptive adversaries, if \(\mathbb {Q}\) is d-disjunct and contains an all-one row.
In the following, without loss of generality we assume that if \(\mathbb {Q}\) is sound for d-corruptive adversaries, \(\mathbb {Q}_1\) is the all-one row.
3.5 Remarks
Multiple Verification Queries. For simplicity the notions defined at Sect. 3.4 require that the adversary uses one query to \(\mathcal {O}_{V}\) or \(\mathcal {O}_{V}^{(i)}\) or \(\mathcal {O}_{I}\). They can be extended so that the adversary can use \(q_v>1\) queries to these oracles, and from the result of [4] we could generally prove that if \(\mathsf {MAC}_{\mathbf K}\) is secure with the case \(q_v=1\), it is also secure when \(q_v>1\). A more rigorous analysis will be given in the full version.
The Need of Tag String Security. We remark that TSF-security notion is rather optional as if \(\mathsf {MAC}_{\mathbf K}\) is secure against tag vector forgery, any forgery is detectable by checking a tag for the all-one row. We think however one may want to quickly check authenticity of a part of data items (\(M\ominus \mathbb {Q}_i\)) by computing tag for \(\mathbb {Q}_i\). Tag computation for \(M\ominus \mathbb {Q}_i\) can be significantly faster than computing a tag for the all-one row. If \(\mathsf {MAC}_{\mathbf K}\) is only TVF-secure and not TSF-secure, a forgery against \(M\ominus \mathbb {Q}_i\) may not be detected until a user performs a tag verification for the all-one row.
Extending CM-security. Notions of TVF and TSF securities allow the adversary to freely choose tags at the final query, while that of CM-security does not (i.e. adversary can not arbitrarily choose \(T'\) in querying \(\mathcal {O}_{I}\), only to choose it from \(T_1,\dots ,T_q\)). However this is unlikely to hold when MAC tags are stored at the same storage as data items. In addition, a user may be interested in corruption localization, that is, finding a superset of corrupted items (i.e. allowing some false positives in the guess) if exact identification of all corrupted items is difficult. These important extensions are already mentioned and independently studied. For example, corruption localization was studied by [8, 11–13], and identification of corrupted items under tag corruption was described at [20].
We remark that these extensions also have been studied in the field of CGT design. If \(M\odot \mathbb {Q}_i\) for some i is not corrupted but \(T[i] = \mathsf {gtm}(i,M\odot \mathbb {Q}_i)\) is corrupted to \(T'[i]\), the corresponding test is considered as invalid, that is, a false positive occurs at the i-th test. Test matrix that can tolerate false positives, and even false negativesFootnote 3, has been studied in the literature, such as Cheraghchi [9], Thierry-Mieg [27] and Ngo et al. [25]. Some of these papers also study the case where final output is only required to be a superset of corrupted items with an allowable margin, which is a form of corruption localization. By using test matrices from these studies, it would be possible to built a GTM scheme having CM-security notion with some extended model allowing a more freedom in choosing a query to \(\mathcal {O}_{I}\) (e.g. \((M',T')\) with \(|\mathsf {diff}(M',M_i)|\le d_1\) and \(|\mathsf {diff}(T',T_i)|\le d_2\) for some \(d_1,d_2\)) and corruption identification with some false positives. Formalizing these ideas and providing a concrete security result using existing results on CGT will be an interesting future direction.
3.6 Provable Security of \(\mathsf {GTM}\)
We first prove that \(\mathsf {gtm}[F_K,G_{K'}]\) is a tweakable PRF for input domain \(\{0,1\}^{\bullet m}\), tweak space \(\mathcal{V}=\{1,\dots ,t\}\). In what follows we fix the \(t\times m\) test matrix \(\mathbb {Q}\) and assume it is sound for d-corruptive adversaries.
Theorem 1
Let \(\mathsf {gtm}[\widetilde{{\mathsf{R}}},\widetilde{{\mathsf{P}}}]:\mathcal{V}\times \{0,1\}^{\bullet m}\rightarrow \{0,1\}^n\) be the tweakable keyed function defined as (2), using a tweakable URF, \(\widetilde{{\mathsf{R}}}\), compatible with \(F_K\) and tweakable URP, \(\widetilde{{\mathsf{P}}}\), compatible with \(G_{K'}\). Then we have
for any adversary \({\mathcal {A}}\) using q queries.
Proof
Let \(\mathsf {gtm}[\widetilde{{\mathsf{R}}},\widetilde{{\mathsf{R}}}']\) be the function that substitutes \(\widetilde{{\mathsf{P}}}\) with \(\widetilde{{\mathsf{R}}}'\), an independent tweakable URF compatible with \(\widetilde{{\mathsf{P}}}\). Let \(\widetilde{{\mathsf{R}}}_{\texttt {gtm}}\) be the tweakable URF compatible with \(\mathsf {gtm}[\widetilde{{\mathsf{R}}},\widetilde{{\mathsf{P}}}]\). Then we have
for some adversaries \({\mathcal {A}}'\), \({\mathcal {A}}''\) using q queries. The first term in the right hand side of (8) is simply bounded by an extended form of PRP/PRF switching lemma (e.g. [6]) and we have \( {\texttt {Adv}}^{ {\texttt {cpa}}}_{\mathsf {gtm}[\widetilde{{\mathsf{R}}},\widetilde{{\mathsf{P}}}],\mathsf {gtm}[\widetilde{{\mathsf{R}}},\widetilde{{\mathsf{R}}}']}({\mathcal {A}}')\le q^2/2^{n+1}\). To analyze the second term, let \((V_i,X_i)\in \{1,\dots ,t\}\times \{0,1\}^{\bullet m}\) with \(X_i=(X_i[1],\dots ,X_i[m])\) be the i-th query of \({\mathcal {A}}''\) accessing \(\mathsf {gtm}[\widetilde{{\mathsf{R}}},\widetilde{{\mathsf{R}}}']\). From the assumption we have \((V_i,X_i)\ne (V_j,X_j)\) if \(i\ne j\). Let \(S_i = \bigoplus _{j=1,\dots ,m,X_i[j]\ne \varepsilon }\widetilde{{\mathsf{R}}}^j(X_i[j])\), which denotes the i-th input (with tweak \(V_i\)) to \(\widetilde{{\mathsf{R}}}'\) for the i-th query made by \({\mathcal {A}}''\) accessing to \(\mathsf {gtm}[\widetilde{{\mathsf{R}}},\widetilde{{\mathsf{R}}}']\). Here \(\widetilde{{\mathsf{R}}}^j\) is not computed for input being \(\varepsilon \) following (2).
Since \(\mathsf {gtm}[\widetilde{{\mathsf{R}}},\widetilde{{\mathsf{R}}}']\) can be seen as a variant of classical Carter-Wegman MAC, the second term is bounded by the collision probability of (V, S) against non-adaptive strategy in the same manner to the analysis of [6, 26], and we have


where the maximum is taken for \((V_1,X_1),\dots ,(V_q,X_q)\). Without loss of generality we focus on the event \(S_1=S_2\) and assume \(X_1[1]\ne X_2[1]\) and \(V_1=V_2\). If \(X_1[1]\ne \varepsilon \) and \(X_2[1]\ne \varepsilon \), \(S_1\oplus S_2 = \widetilde{{\mathsf{R}}}^{(1)}(X_1[1])\oplus \widetilde{{\mathsf{R}}}^{(1)}(X_2[1]) \oplus \delta \), where \(\delta \) is independent of \(\widetilde{{\mathsf{R}}}^{(1)}\) (as it is a sum of some outputs of \(\widetilde{{\mathsf{R}}}^{(2)},\dots ,\widetilde{{\mathsf{R}}}^{(m)}\) or \(0^n\)). If \(X_1[1]= \varepsilon \) and \(X_2[1] = x \ne \varepsilon \) (or vice versa), \(S_1\oplus S_2 = \widetilde{{\mathsf{R}}}^{(1)}(x) \oplus \delta \) holds. For both cases the probability of \(S_1\oplus S_2 = 0^n\) is clearly \(1/2^n\). Thus the right hand side of (10) is bounded by \(\left( {\begin{array}{c}q\\ 2\end{array}}\right) /2^n < q^2/2^{n+1}\). This concludes the proof. \(\quad \square \)
Theorem 2
Let \(\widetilde{{\mathsf{R}}}\) and \(\widetilde{{\mathsf{P}}}\) be the tweakable URF and tweakable URP compatible with \(F_K\) and \(G_{K'}\) in \(\mathsf {GTM}[F_K,G_{K'}]\). Then, we have



where \({\mathcal {A}}_j\) for \(j=1,2,3\) uses q queries to \(\mathcal {O}_{T}\) and a query to \(\mathcal {O}_{V}\) (for \(j=1\)) or \(\mathcal {O}_{V}^{(i)}\) (for \(j=2\)) or \(\mathcal {O}_{I}\) (for \(j=3\)).
Proof
For (11), let \(\widetilde{{\mathsf{R}}}_{\texttt {gtm}}\) be the tweakable URF compatible with \(\mathsf {gtm}[\widetilde{{\mathsf{R}}},\widetilde{{\mathsf{P}}}]\). Let \({\mathsf{R}}_i:\{0,1\}^{*c_i}\rightarrow \{0,1\}^n\) be the independent URF where \(c_i=|\mathcal{I}(\mathbb {Q}_i)|\), and let \(\widetilde{{\mathsf{R}}}_{\texttt {GTM}}\) be an ideal primitive for \(\mathsf {GTM}[\widetilde{{\mathsf{R}}},\widetilde{{\mathsf{P}}}]\), which takes \(M\in \{0,1\}^{*m}\) and outputs \(T=(T[1],\dots ,T[t])\) for \(T[i]={\mathsf{R}}_i(M\ominus \mathbb {Q}_i)\). We observe that a tagging query to \(\mathsf {GTM}[\widetilde{{\mathsf{R}}},\widetilde{{\mathsf{P}}}]\) yields queries to \(\mathsf {gtm}[\widetilde{{\mathsf{R}}},\widetilde{{\mathsf{P}}}](i,\cdot )\) for each \(i=1,\dots ,t\). Thus we have
where \({\mathcal {A}}_1'\) uses \(q+1\) queries, and \({\mathcal {A}}_1''\) uses \(t(q+1)\) queries. The second inequality follows from the fact that, to forge \(\widetilde{{\mathsf{R}}}_{\texttt {GTM}}\), the adversary has to guess \(T'[1]={\mathsf{R}}_1(M'\ominus \mathbb {Q}_1)={\mathsf{R}}_1(M')\) given tags for \(M_1,\dots ,M_q\) for certain \(M'\ne ^\forall M_i\). Thus \(T'[1]\) is independent and uniformly random over n bits. The last inequality follows from Theorem 1.
For (12), the bound is similarly derived as



where \({\mathcal {A}}_2''\) uses \((tq+1)\) queries to \(\mathsf {gtm}[\widetilde{{\mathsf{R}}},\widetilde{{\mathsf{P}}}](i,\cdot )\) or \(\widetilde{{\mathsf{R}}}_{\texttt {gtm}}(i,\cdot )\). The second inequality follows from that the adversary needs to guess \({\mathsf{R}}_i(M'\ominus \mathbb {Q}_i)\) for some \(M'\) satisfying \(M'\ominus \mathbb {Q}_i\ne M_1\ominus \mathbb {Q}_i,\dots ,M_q\ominus \mathbb {Q}_i\), and the last follows from Theorem 1.
For (13), we observe that the adversary must find a pair of distinct M and \(M'\) causing an exploitable collision between tag strings, throughout accessing tagging oracle, since otherwise it reduces to the original combinatorial problem setting where tests never fail, and thus the identification oracle never fails due to d-disjunctness of \(\mathbb {Q}\). Here, an exploitable collision means that there exists a pair of distinct \((M,M')\) such that for some \(i\in \{1,\dots ,t\}\) with \(M\ominus \mathbb {Q}_i\ne M'\ominus \mathbb {Q}_i\) we have \(T[i]= T'[i]\), for \((T[1],\dots ,T[t]) = \mathsf {GTM}[\widetilde{{\mathsf{R}}},\widetilde{{\mathsf{P}}}](M)\) and \((T'[1],\dots ,T'[t]) = \mathsf {GTM}[\widetilde{{\mathsf{R}}},\widetilde{{\mathsf{P}}}](M')\). Here, note that an exploitable collision at the final identification query directly means a win but an exploitable collision invoked at tagging queries also implies a win. Hence the advantage is bounded by the probability of exploitable collision throughout the game.
We then define a collision-finding game, where adversary \({\mathcal {A}}\) (adaptively) queries a tagging oracle implementing a GTM, \(\mathsf {MAC}_{\mathbf K}\). Let \(M_i\in \{0,1\}^{*m}\) be the i-th query and \(T_i\in (\{0,1\}^n)^t\) be the i-th response. We assume \({\mathcal {A}}\) never makes duplicate queries, and say \({\mathcal {A}}\) wins there is an exploitable collision, i.e. \(T_i[h]=T_j[h]\) for some \(1\le i< j\le q\) and \(h\in \{1,\dots ,t\}\), and we denote the probability of win by  . Then we have
. Then we have



where \({\mathcal {A}}_3'\) uses \((q+1)\) queries, \({\mathcal {A}}_3''\) uses \(t(q+1)\) queries. The first term of the last inequality follows from Theorem 1, and the second term follows from the fact that \(\widetilde{{\mathsf{R}}}_{\texttt {GTM}}\)’s outputs are completely random and a simple counting of events (\(T_i[h]=T_j[h]\) for some \(1\le i< j\le q\) and \(h\in \{1,\dots ,t\}\)) having probability \(1/2^n\). This concludes the proof. \(\quad \square \)
Practical Instantiations. The above analysis shows security bounds based on information-theoretic primitives, however we can easily derive the security bounds with practical instantiations having computational security. For concrete instantiations, \(\widetilde{{\mathsf{R}}}\) in \(\mathsf {gtm}[\widetilde{{\mathsf{R}}},\widetilde{{\mathsf{P}}}]\) can be instantiated by HMAC-SHA2 or CMAC [2] with AES, where tweak is (e.g.) encoded into a fixed-length sequence and prepended to to input. Also \(\widetilde{{\mathsf{P}}}\) can be instantiated by a computationally-secure TBC. It can be instantiated by a blockcipher mode of operation such as XEX [26] or a dedicated constructions, such as Threefish [18] or TBCs by Jean et al. [22] which are used in their proposals for CAESAR competition for authenticated encryption [1]. If we use CMAC with n-bit URP for \(\widetilde{{\mathsf{R}}}\) and XEX with another n-bit URP for \(\widetilde{{\mathsf{P}}}\), and each data item is at most \(n\ell \) bits, then combining the provable security bounds of CMAC, shown by Iwata and Kurosawa [21], and XEX and Theorem 2, the resulting security bounds (for TVF, TSF and CM) are shown to be \(O(\sigma ^2/2^n)\), where \(\sigma =q\ell w \le q\ell mt\) and \(w={\text{ Hw }}(\mathbb {Q})\) with a small constant. When URP is substituted with a real blockcipher, deriving computational counterparts is also standard, see e.g. Bellare et al. [3].
4 Experimental Implementation
We implemented our algorithm with two existing CGT methods. The first is Shifted Traversal Design (STD) by Thierry-Mieg [27]. Thierry-Mieg and Bailly also developed a tool to produce CGT test matrix based on STD, Interpool [28]. The second is Chinese Reminder Sieve (CRS) proposed by Eppstein et al. [16].
The first method, STD, is based on the repetition and rotation of sub-matrix. A parameter set of STD is written as (n, q, k), where n denotes the number of items, q denotes the number of tests in a layer and k denotes the number of layers. Here k specifies redundancy in the design and each item is included exactly in k tests. We need q to be a prime and \(q<n\) and \(k\le q+1\). The number of tests is \(q\cdot k\). Each test contains \(\lfloor n/q \rfloor \) or \(\lfloor n/q \rfloor +1\) items. Let \(\Gamma (q,n)\) be \(\min \{\gamma :q^{\gamma +1}\ge n\}\). Then STD can identify t corrupted items if \(t\cdot \Gamma (q,n) \le q\) and \(k=t\cdot \Gamma (q,n) +1\) hold. Moreover with E observation errors (false positives or negatives) it works if \(t\cdot \Gamma (q,n)+2E \le q\) and \(k=t\cdot \Gamma (q,n) +2E+1\) hold. See [27] for details.
The second method, CRS, is based on number theory and its test matrix is specified by a sequence of powers of primes, \((t_1,\dots ,t_k)=(p_1^{e_1},\dots ,p_k^{e_k})\), satisfying \(\prod _{j}t_j\ge n^d\), where n denotes the number of items and d denotes the number of corrupted items that can be identified. Test matrix consists of k sub-matrices and j-th sub-matrix is determined by \(t_j\) and has \(t_j\) rows (tests). Thus CRS consists of \(t=\sum _{j}t_j\) tests. Reference [16] suggests a backtracking search to find an appropriate sequence \((t_1,\dots ,t_k)\) and shows a Python code doing it.
Details. We chose several parameter settings for both STD and CRS methods, and implemented our algorithm for tag computation. Verification and corruption identification procedures are not implemented at this moment. For STD we chose \((n,q,k)=(940,13,13)\) with 169 tests and (2000, 11, 11) with 121 tests, and for CRS we chose \((n,d)=(10^4,2)\) and \((10^4,5)\) and \((10^5,2)\). Number of tests are 89, 378, and 131 respectively. We did not include the all-one row as the effect to performance is quite small.
To implement \(\mathsf {GTM}[F_K,G_{K'}]\), we used CMAC for \(F^j_K\), where tweak j is encoded as a 4-byte sequence and prepended to the input, and used XEX for \(G^i_{K'}\), both with AES-128. Each tag is 16 bytes. For storing a large binary test matrix, a natural way is to have an array, A[i][j], which denotes the j-th item index to be included in the i-th test, as employed by Interpool. In C language we can store it as a two-dimensional array of pointers. This expression, which we call item-index expression, is however quite inefficient to implement \(\mathsf {GTM}[F_K,G_{K'}].\text{ Tag }\) in Fig. 1, since it incurs a search over A for every item. Instead we made the inverse array, B[i][j], which denotes the j-th test index used in the i-th item, which we call test-index expression. Using this expression the algorithm of Fig. 1 is easily implemented, where lines 4 and 5 are replaced with simple successive reading of array B.
For comparison we also implemented a conventional computation of \(\mathsf {gtm}[F_K,G_{K'}]\), which uses \(\mathsf {gtm}[F_K,G_{K'}](i,\cdot )\) as a black-box tweakable MAC function for each test index i, using item-index array. This needs \({\text{ Hw }}(\mathbb {Q})\) calls of F and t calls of G.
We used a standard C implementation of AES using four 1K-byte tables, called T-tables, on Intel CPU (Ivybridge Core i7 3770, 3.4 GHz), running 64-bit Windows. Here AES-128 runs at 13.3 cycles/byte.
The implementation results are shown in Table 1 for STD and Table 2 for CRS, where each item has a fixed length, from 16 to 2048 bytes, shown in the first row. The data items are randomly generated. The figures denote the average cycles for input byte (i.e. total cycles divided by the total bytes of all data items). These tables show that the speed of our algorithm is much faster than the conventional one, and it is mostly the same as AES itself if each data item is more than 1K bytes. In theory the speed-up of the proposed scheme from the conventional one is proportional to \({\text{ Hw }}(\mathbb {Q})/(m+t)\) for m items and t tests. The actual speed-up factor is 8 to 15 in our experiments for data items of 2K bytes, and the difference from the ratio \({\text{ Hw }}(\mathbb {Q})/(m+t)\) is quite small.
5 Concluding Remarks
This paper has studied a class of MAC function which is used with combinatorial group testing to identify the part of corruption. While such MAC function generally needs O(mt) computation for m data items and t tests, we propose to use a variant of PMAC to reduce the cost to \(O(m+t)\) irrespective of the contents of these tests. From our experiments, we observe that an AES-based implementation of our scheme can in fact run as fast as AES itself for practical size of problems. An important next direction is to investigate practical impact of our proposal to real-life security applications for which a group testing MAC is useful.
Interestingly, the idea shown here can not work fine in the keyless setting, say by replacing F and G by keyless hash functions, since the resulting incremental hash function is quite weak against generalized birthday attack [29], and thus we need to greatly increase the internal state (the output size of F). The problem here seems deeply related to the construction of secure, space-efficient incremental hash function, and needs further study.
Notes
- 1.
Unless entire input is an empty string.
- 2.
It is also written as \(\overline{d}\)-separable, and in this case d-separable means that unions of exactly d columns are distinct.
- 3.
It corresponds to successful MAC forgeries, which we consider negligibly small chance to occur.
References
CAESAR : competition for authenticated encryption: security, applicability, and robustness. http://competitions.cr.yp.to/index.html/
Recommendation for block cipher modes of operation: the CMAC mode for authentication. NIST special publication 800–38B (2005), national institute of standards and technology
Bellare, M., Desai, A., Jokipii, E., Rogaway, P.: A concrete security treatment of symmetric encryption. In: FOCS 1997, pp. 394–403. IEEE Computer Society (1997). http://dx.doi.org/10.1109/SFCS.1997.646128
Bellare, M., Goldreich, O., Mityagin, A.: The Power of verification queries in message authentication and authenticated encryption. Cryptology ePrint Archive, Report 2004/309 (2004). http://eprint.iacr.org/
Bellare, M., Kilian, J., Rogaway, P.: The security of the cipher block chaining message authentication code. J. Comput. Syst. Sci. 61(3), 362–399 (2000)
Black, J.A., Rogaway, P.: CBC MACs for arbitrary-length messages: the three-key constructions. In: Bellare, M. (ed.) CRYPTO 2000. LNCS, vol. 1880, pp. 197–215. Springer, Heidelberg (2000)
Black, J.A., Rogaway, P.: A block-cipher mode of operation for parallelizable message authentication. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 384–397. Springer, Heidelberg (2002). http://dx.doi.org/10.1007/3-540-46035-7_25
De Bonis, A., Di Crescenzo, G.: Combinatorial group testing for corruption localizing hashing. In: Fu, B., Du, D.-Z. (eds.) COCOON 2011. LNCS, vol. 6842, pp. 579–591. Springer, Heidelberg (2011). http://dx.doi.org/10.1007/978-3-642-22685-4_50
Cheraghchi, M.: Noise-resilient group testing: limitations and constructions. Discrete Appl. Math. 161(1–2), 81–95 (2013). http://dx.doi.org/10.1016/j.dam.2012.07.022
Di Crescenzo, G., Arce, G.: Data forensics constructions from cryptographic hashing and coding. In: Shi, Y.Q., Kim, H.-J., Perez-Gonzalez, F. (eds.) IWDW 2011. LNCS, vol. 7128, pp. 494–509. Springer, Heidelberg (2012). http://dx.doi.org/10.1007/978-3-642-32205-1_39
Di Crescenzo, G.D., Ge, R., Arce, G.R.: Design and analysis of DBMAC, an error localizing message authentication code. In: GLOBECOM 2004, pp. 2224–2228. IEEE (2004). http://dx.doi.org/10.1109/GLOCOM.2004.1378404
Di Crescenzo, G., Jiang, S., Safavi-Naini, R.: Corruption-localizing hashing. In: Backes, M., Ning, P. (eds.) ESORICS 2009. LNCS, vol. 5789, pp. 489–504. Springer, Heidelberg (2009). http://dx.doi.org/10.1007/978-3-642-04444-1_30
Di Crescenzo, G.D., Vakil, F.: Cryptographic hashing for virus localization. In: Jahanian, F. (ed.) WORM 2006. pp. 41–48. ACM Press (2006). http://doi.acm.org/10.1145/1179542.1179550
Dorfman, R.: The detection of defective members of large populations. Ann. Math. Stat. 14(4), 436–440 (1943)
Du, D., Hwang, F.: Combinatorial Group Testing and Its Applications: Series on Applied Mathematics. World Scientific, Singapore (2000). http://books.google.co.jp/books?id=KW5-CyUUOggC
Eppstein, D., Goodrich, M.T., Hirschberg, D.S.: Improved combinatorial group testing algorithms for real-world problem sizes. SIAM J. Comput. 36(5), 1360–1375 (2007). http://dx.doi.org/10.1137/050631847
Fang, J., Jiang, L.Z., Yiu, S., Hui, L.C.: Hard disk integrity check by hashing with combinatorial group testing. In: CSA 2009, pp. 1–6 (2009). http://dx.doi.org/10.1109/CSA.2009.5404206
Ferguson, N., Lucks, S., Schneier, B., Whiting, D., Bellare, M., Kohno, T., Callas, J., Walker, J.: Skein hash function. SHA-3 Submission (2008). http://www.skein-hash.info/
Goldreich, O.: Modern Cryptography, Probabilistic Proofs and Pseudorandomness. Algorithms and Combinatorics. Springer, Heidelberg (1998)
Goodrich, M.T., Atallah, M.J., Tamassia, R.: Indexing information for data forensics. In: Ioannidis, J., Keromytis, A.D., Yung, M. (eds.) ACNS 2005. LNCS, vol. 3531, pp. 206–221. Springer, Heidelberg (2005). http://dx.doi.org/10.1007/11496137_15
Iwata, T., Kurosawa, K.: OMAC: one-key CBC MAC. In: Johansson, T. (ed.) FSE 2003. LNCS, vol. 2887, pp. 129–153. Springer, Heidelberg (2003)
Jean, J., Nikolic, I., Peyrin, T.: Tweaks and keys for block ciphers: the TWEAKEY framework. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8874, pp. 274–288. Springer, Heidelberg (2014). http://dx.doi.org/10.1007/978-3-662-45608-8_15
Liskov, M., Rivest, R.L., Wagner, D.: Tweakable block ciphers. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 31–46. Springer, Heidelberg (2002). http://dx.doi.org/10.1007/3-540-45708-9_3
Ngo, H.Q., Du, D.Z.: A Survey on combinatorial group testing algorithms with applications to DNA library screening. DIMACS Series in Discrete Mathematics and Theoretical Computer Science (2000)
Ngo, H.Q., Porat, E., Rudra, A.: Efficiently decodable error-correcting list disjunct matrices and applications (Extended Abstract). In: Aceto, L., Henzinger, M., Sgall, J. (eds.) ICALP 2011, Part I. LNCS, vol. 6755, pp. 557–568. Springer, Heidelberg (2011). http://dx.doi.org/10.1007/978-3-642-22006-7_47
Rogaway, P.: Efficient instantiations of tweakable blockciphers and refinements to modes OCB and PMAC. In: Lee, P.J. (ed.) ASIACRYPT 2004. LNCS, vol. 3329, pp. 16–31. Springer, Heidelberg (2004). http://dx.doi.org/10.1007/978-3-540-30539-2_2
Thierry-Mieg, N.: A new pooling strategy for high-throughput screening: the shifted transversal design. BMC Bioinform. 7, 28 (2006). http://www.biomedcentral.com/content/pdf/1471-2105-7-28.pdf
Thierry-Mieg, N., Bailly, G.: Interpool: interpreting smart-pooling results. Bioinformatics 24(5), 696–703 (2008)
Wagner, D.: A generalized birthday problem. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 288–304. Springer, Heidelberg (2002). http://dx.doi.org/10.1007/3-540-45708-9_19
Zaverucha, G.M., Stinson, D.R.: Group testing and batch verification. In: Kurosawa, K. (ed.) ICITS 2009. LNCS, vol. 5973, pp. 140–157. Springer, Heidelberg (2010). http://dx.doi.org/10.1007/978-3-642-14496-7_12
Acknowledgments
The author would like to thank Kengo Mori, Jun Furukawa and Toshihiko Okamura for fruitful discussions, and Hiroyasu Kubo for initial-stage implementation, and anonymous reviewers for helpful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Minematsu, K. (2015). Efficient Message Authentication Codes with Combinatorial Group Testing. In: Pernul, G., Y A Ryan, P., Weippl, E. (eds) Computer Security -- ESORICS 2015. ESORICS 2015. Lecture Notes in Computer Science(), vol 9326. Springer, Cham. https://doi.org/10.1007/978-3-319-24174-6_10
Download citation
DOI: https://doi.org/10.1007/978-3-319-24174-6_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-24173-9
Online ISBN: 978-3-319-24174-6
eBook Packages: Computer ScienceComputer Science (R0)






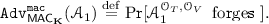
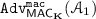 is negligibly small for all practical adversaries.
is negligibly small for all practical adversaries.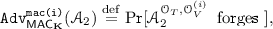
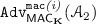 is negligibly small for all practical adversaries, for all
is negligibly small for all practical adversaries, for all 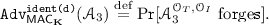
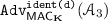 is negligibly small for all practical d-corrupting adversaries.
is negligibly small for all practical d-corrupting adversaries.