Abstract
Exchanging resources often involves situations where a participant gives a resource without obtaining immediately the expected reward. For instance, one can buy an item without paying it in advance, but contracting a debt which must be eventually honoured. Resources, credits and debits can be represented, either implicitly or explicitly, in several formal models, among which Petri nets and linear logic. In this paper we study the relations between two of these models, namely intuitionistic linear logic with mix and Debit Petri nets. In particular, we establish a natural correspondence between provability in the logic, and marking reachability in nets.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
References
Hobbes, T.: The Leviathan, chap. XIV (1651)
Viswanathan, M., Viswanathan, R.: Foundations for circular compositional reasoning. In: Orejas, F., Spirakis, P.G., van Leeuwen, J. (eds.) ICALP 2001. LNCS, vol. 2076, pp. 835–847. Springer, Heidelberg (2001). doi:10.1007/3-540-48224-5_68
Maier, P.: Compositional circular assume-guarantee rules cannot be sound and complete. In: Gordon, A.D. (ed.) FOSSACS 2003. LNCS, vol. 2620, pp. 343–357. Springer, Heidelberg (2003). doi:10.1007/3-540-36576-1_22
Bartoletti, M., Zunino, R.: A calculus of contracting processes. In: Proceedings of the LICS, pp. 332–341 (2010). doi:10.1109/LICS.2010.25
Bartoletti, M., Cimoli, T., Pinna, G.M., Zunino, R.: Circular causality in event structures. Fundamenta Informaticae 134(3–4), 219–259 (2014). doi:10.3233/FI-2014-1101
Bartoletti, M., Cimoli, T., Giamberardino, P.D., Zunino, R.: Vicious circles in contracts and in logic. Sci. Comput. Program. (to appear). doi:10.1016/j.scico.2015.01.005
Bartoletti, M., Cimoli, T., Pinna, G.M., Zunino, R.: Contracts as games on event structures, JLAMP (to appear). doi:10.1016/j.jlamp.2015.05.001
Girard, J.-Y.: Linear logic. Theoret. Comput. Sci. 50, 1–102 (1987). doi:10.1016/0304-3975(87)90045-4
Martí-Oliet, N., Meseguer, J.: An algebraic axiomatization of linear logic models. In: Topology and Category Theory in Computer Science, pp. 335–355. Oxford University Press Inc. (1991)
Fleury, A., Retoré, C.: The Mix rule. Mathematical Structures in Computer Science 4(2), 273–285 (1994). doi:10.1017/S0960129500000451
Kamide, N.: Linear logics with communication-merge. J. Logic Comput. 15(1), 3–20 (2005). doi:10.1093/logcom/exh029
Stotts, P.D., Godfrey, P.: Place/transition nets with debit arcs. Inf. Process. Lett. 41(1), 25–33 (1992). doi:10.1016/0020-0190(92)90076-8
Reisig, W.: Petri Nets: An Introduction. Monographs in Theoretical Computer Science, vol. 4. Springer, Heidelberg (1985). doi:10.1007/978-3-642-69968-9
Kanovich, M.I.: Linear logic as a logic of computations. Ann. Pure Appl. Logic 67, 183–212 (1994). doi:10.1016/0168-0072(94)90011-6
Kanovich, M.I.: Petri nets, Horn programs, linear logic and vector games. Ann. Pure Appl. Logic 75(1–2), 107–135 (1995). doi:10.1016/0168-0072(94)00060-G
Asperti, A., Ferrari, G.L., Gorrieri, R.: Implicative formulae in the “proofs as computations” analogy. In: Proceedings of the POPL, pp. 59–71 (1990). doi:10.1145/96709.96715
Engberg, U., Winskel, G.: Completeness results for linear logic on Petri nets. Ann. Pure Appl. Logic 86(2), 101–135 (1997). doi:10.1016/S0168-0072(96)00024-3
Martí-Oliet, N., Meseguer, J.: From Petri nets to linear logic. Math. Struct. Comput. Sci. 1(1), 69–101 (1991). doi:10.1017/S0960129500000062
Ishihara, K., Hiraishi, K.: The completeness of linear logic for Petri net models. Logic J. IGPL 9(4), 549–567 (2001)
Kanovich, M.I., Okada, M., Scedrov, A.: Phase semantics for light linear logic. ENTCS 6, 221–234 (1997). doi:10.1016/S1571-0661(05)80159-8
Bartoletti, M., Cimoli, T., Pinna, G.M.: Lending Petri nets and contracts. In: Arbab, F., Sirjani, M. (eds.) FSEN 2013. LNCS, vol. 8161, pp. 66–82. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40213-5_5
Bartoletti, M., Cimoli, T., Pinna, G.M.: Lending Petri nets. Sci. Comput. Program. (2015). doi:10.1016/j.scico.2015.05.006
Acknowledgments
This work has been partially supported by Aut. Reg. of Sardinia grants L.R.7/2007 CRP-17285 (TRICS) and P.I.A. 2010 (“Social Glue”), by MIUR PRIN 2010-11 project “Security Horizons”, and by EU COST Action IC1201 “Behavioural Types for Reliable Large-Scale Software Systems” (BETTY).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Proofs
A Proofs
1.1 A.1 Proofs for Sect. 4.1
Lemma 1
If \((W, \varGamma , ! \varDelta ) \Downarrow Z\) then \(W, \varGamma , ! \varDelta \vdash Z\).
Proof
We proceed by induction on the height of the derivation of \((W, \varGamma , !\varDelta ) \Downarrow Z\). We have the following cases, according on the last rule used:
-
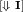 ,
,  ,
,  ,
,  , or
, or  . Straightfoward.
. Straightfoward. -
 . We have:
. We have: 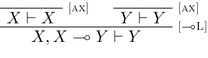
and we obtain the thesis as follows:
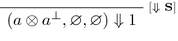
-
 . We have:
. We have: 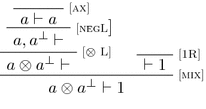
and we obtain the thesis as follows:
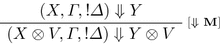
-
 . We have:
. We have: 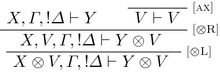
and by using the induction hypothesis, we obtain the thesis as follows:
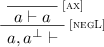
\(\square \)
Definition 9
(Almost-Horn honoured sequent). We say that a sequent \(\varOmega ,\varGamma , !\varDelta \vdash \gamma \) is almost-Horn honoured if \(\varOmega \) is a multiset of simple products, \(\varGamma , \varDelta \) are multisets of Horn implications, and \(\gamma \) is a positive simple product or empty.
Definition 10
(Clean proof). We say that proof \(\pi \) of an almost-Horn honoured sequent \(\varOmega , \varGamma , \varDelta \vdash \gamma \) is clean when all the applications of a rule [negL] in \(\pi \) are placed just below an [Ax] rule, as follows:

Lemma 2
Any provable almost-Horn honoured sequent admits a clean cut-free proof.
Proof
Let \(\varOmega , \varGamma , \varDelta \vdash \gamma \) be a provable almost-Horn honoured sequent. By Theorem 1 it admits a cut-free proof \(\pi \). We show that every occurrence of the rule [negL] which does not respect the pattern of Definition 10, can be moved upwards in the proof. We reason by cases, depending on the rule r just above [negL] in \(\pi \). Since \(\pi \) is cut-free and all its sequents are almost-Horn honoured, we can restrict to the following cases:
-
[Ax], [1L],
 ,
,  , [weakL], [coL]. Straightforward.
, [weakL], [coL]. Straightforward. -
[Mix]. We have:
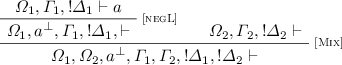
and we obtain the thesis as follows:
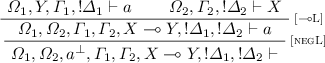
-
 . We have:
. We have: 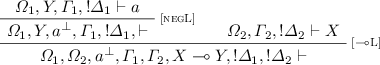
and we obtain the thesis as follows:
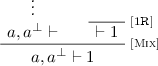
\(\square \)
Definition 11
(Proper proof). For a proof \(\pi \) of \({\text {ILL}}^{mix}\), we say that an application of [Mix] rule is proper, whenever it has the following form:

We say that a proof \(\pi \) of an honoured almost-Horn sequent is proper if it is clean, and every occurrence of the [Mix] rule in \(\pi \) is proper.
Definition 12
(Harmless cut). Given a proof \(\pi \) of \({\text {ILL}}^{mix}\), we say that the application of a [Cut] rule is harmless whenever it has the following form:

where W is a positive simple product.
Lemma 3
A provable Horn honoured sequent admits a proper proof where all the applications of the [Cut] rule are harmless.
Proof
We prove the following stronger statement. Assume that an almost-Horn honoured sequent \(\varOmega , \varGamma , !\varDelta \vdash \gamma \) is provable. Then:
-
(a)
if \(\gamma = Z\), then there exists a proper proof of \(\varOmega , \varGamma , !\varDelta \vdash Z\) where all [Cut] rules are harmless.
-
(b)
if \(\gamma \) is empty, then there exists a proper proof of \(\varOmega , \varGamma , !\varDelta \vdash 1\) where all [Cut] rules are harmless.
By Lemma 2, consider a clean cut-free proof \(\pi \) of the sequent. We proceed by induction on the height of \(\pi \). Since \(\pi \) is cut-free, we can restrict to the following cases, according to the last rule used in \(\pi \):
-
[Ax], [1R]. In these cases there is nothing to prove.
-
[1L],
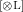 ,
,  ,
,  ,
,  , [weakL], [coL]. Straightforward by the induction hypothesis.
, [weakL], [coL]. Straightforward by the induction hypothesis. -
[negL]. Since \(\pi \) is clean, is must have the following form:
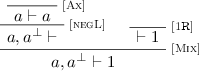
which we replace with the following proof:
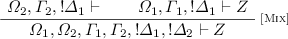
-
[negR]. This case is not possible, since \(\pi \) is cut-free and \(\gamma \) is either a positive simple product or empty.
-
[Mix]. We have the following two subcases:
-
1.
\(\pi \) has the form:
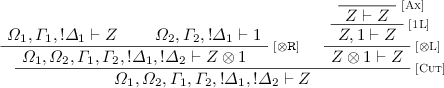
By the induction hypothesis (applied on both premises), we obtain:
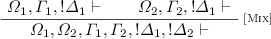
where the application of the [Cut] rule is harmless.
-
2.
\(\pi \) has the form:
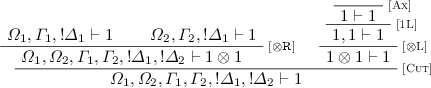
By the induction hypothesis and harmless application of [Cut], we obtain:
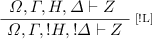
where the application of the [Cut] rule is harmless. \(\square \)
-
1.
Lemma 4
Let \(\varOmega , \varGamma , !\varDelta \vdash Z\) be a provable honoured Horn sequent. Then:
Proof
By Lemma 3, there exists a proper proof \(\pi \) of \(\varOmega , \varGamma , ! \varDelta \vdash Z\) containing only harmless applications of the [Cut] rule. We proceed by induction on the height of \(\pi \), and then by cases on the last rule used.
-
[Ax]. Trivial by rule
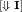 .
. -
[!L]. We have:
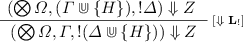
By the induction hypothesis, we obtain:
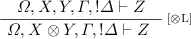
-
[negL]. This case is not possible, since the righthand side of the final sequent of \(\pi \) cannot be empty by hypothesis.
-
[negR]. This case is not possible, since the righthand side of the final sequent of \(\pi \) must be a positive simple product.
-
 . We have:
. We have: 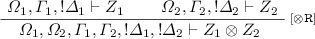
By the induction hypothesis,
 . The thesis follows because
. The thesis follows because  .
. -
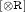 . We have:
. We have: 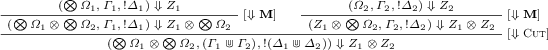
By applying the induction hypothesis on both premises, we obtain:
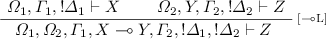
-
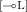 . We have:
. We have: 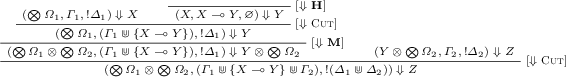
Since \(X \multimap Y\) is a Horn implication, then X must be a positive simple product, and so \(\varOmega _1, \varGamma _1, !\varDelta _1 \vdash X\) is an honoured Horn sequent. Therefore we can apply the induction hypothesis, from which we obtain:
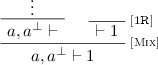
-
[Mix]. Since \(\pi \) is proper, it must be:
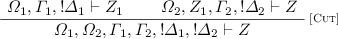
and the thesis follows from rule
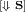 .
. -
[Cut]. Since \(\pi \) contains only harmless cuts, by Definition 12 there exist \(\varOmega _1,\varOmega _2,Z_1\), \(\varGamma _1,\varGamma _2\), and \(\varDelta _1,\varDelta _2\) such that \(Z_1\) is honoured, and the last rule in \(\pi \) is:
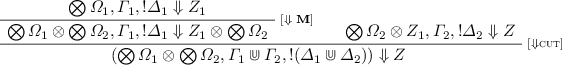
By applying the induction hypothesis on both premises, we obtain:
$$ \bigotimes \varOmega _1, \varGamma _1, ! \varDelta _1 \Downarrow Z_1 \qquad \bigotimes \varOmega _2 \otimes Z_1, \varGamma _2, ! \varDelta _2 \Downarrow Z $$Therefore, we obtain:
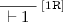
-
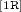 . We have:
. We have: 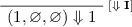
Since the empty multiset is associated with the simple product 1, we obtain:
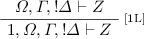
-
 . We have:
. We have: 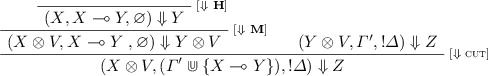
By the induction hypothesis, we know that:
$$ (\bigotimes \varOmega , \varGamma , !\varDelta ) \Downarrow Z $$Since \(mset_{\bigotimes \varOmega }=mset_{1 \otimes \bigotimes \varOmega }\), we conclude that:
$$ (1 \otimes \bigotimes \varOmega , \varGamma , !\varDelta ) \Downarrow Z $$\(\square \)
Theorem 2. Let \(\varOmega , \varGamma , !\varDelta \vdash Z\) be an honoured Horn sequent. Then:
Proof
The (\(\Longrightarrow \)) direction follows from Lemma 1; the (\(\Longleftarrow \)) direction follows from Lemma 4. \(\square \)
1.2 A.2 Proofs for Sect. 4.2
Lemma 5
The following facts hold:
-
1.
If \((W_1, \varGamma _1, ! \varDelta _1) \overset{}{\leadsto }^{*} (W_2, \varGamma '_1, ! \varDelta _1)\) and \((W_2, \varGamma _2, ! \varDelta _2) \overset{}{\leadsto }^{*} (W_3, \varGamma '_2, ! \varDelta _2)\), then
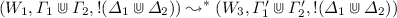 .
. -
2.
If \((W, \varGamma , ! \varDelta ) \overset{}{\leadsto }^{*} (W', \varGamma ', ! \varDelta )\) and V is a simple product, then \((W \otimes V, \varGamma , ! \varDelta ) \overset{}{\leadsto }^{*} (W' \otimes V, \varGamma ', ! \varDelta )\).
-
3.
If
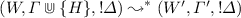 where H is a Horn implication, then
where H is a Horn implication, then 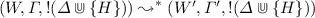 .
. -
4.
If \((W, \varGamma , ! \varDelta ) \overset{}{\leadsto }^{*} (W', \varGamma ', ! \varDelta )\) where H is a Horn implication, then
 .
. -
5.
If
 where H is a Horn implication, then
where H is a Horn implication, then  .
.
Proof
Straightforward. \(\square \)
Proposition 1. \( (W,\varGamma , ! \varDelta ) \Downarrow Z \iff (W, \varGamma , !\varDelta ) \leadsto ^*(Z, \varnothing , !\varDelta ) \)
Proof
For the \((\Longrightarrow )\) direction, we proceed by induction on the height of the derivation of \(( W,\varGamma , ! \varDelta ) \Downarrow Z\), and then by cases on the last rule applied.
For the base case, we have three possible subcases:
-
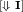 . By reflexivity of \(\overset{}{\leadsto }^{*}\)
\((X, \varnothing , \varnothing ) \overset{}{\leadsto }^{*} (X, \varnothing , \varnothing )\).
. By reflexivity of \(\overset{}{\leadsto }^{*}\)
\((X, \varnothing , \varnothing ) \overset{}{\leadsto }^{*} (X, \varnothing , \varnothing )\). -
 . By rule
. By rule 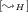 , \((X, X \multimap Y, \varnothing ) \overset{}{\leadsto } (Y, \varnothing , \varnothing )\).
, \((X, X \multimap Y, \varnothing ) \overset{}{\leadsto } (Y, \varnothing , \varnothing )\). -
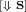 . By rule
. By rule  , \((a\otimes a^{\perp }, \varnothing , \varnothing ) \overset{}{\leadsto } (1, \varnothing , \varnothing )\).
, \((a\otimes a^{\perp }, \varnothing , \varnothing ) \overset{}{\leadsto } (1, \varnothing , \varnothing )\).
For the inductive case, we have the following subcases:
-
 . By applying the induction hypothesis on both premises, we obtain: $$ (W, \varGamma _1, !\varDelta _1) \leadsto ^* (U, \varnothing , !\varDelta _1) \quad \quad (U, \varGamma _2, !\varDelta _2) \leadsto ^* (Z, \varnothing , !\varDelta _2) $$
. By applying the induction hypothesis on both premises, we obtain: $$ (W, \varGamma _1, !\varDelta _1) \leadsto ^* (U, \varnothing , !\varDelta _1) \quad \quad (U, \varGamma _2, !\varDelta _2) \leadsto ^* (Z, \varnothing , !\varDelta _2) $$By item (1) of Lemma 5 we obtain the thesis:

-
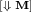 . By the induction hypothesis and item (2) of Lemma 5.
. By the induction hypothesis and item (2) of Lemma 5. -
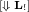 . By the induction hypothesis and item (3) of Lemma 5.
. By the induction hypothesis and item (3) of Lemma 5. -
 . By the induction hypothesis and item (4) of Lemma 5.
. By the induction hypothesis and item (4) of Lemma 5. -
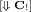 . By the induction hypothesis and item (5) of Lemma 5.
. By the induction hypothesis and item (5) of Lemma 5.
For the (\(\Longleftarrow \)) direction, we proceed by induction on the length n of the computation \((W, \varGamma , !\varDelta ) \leadsto ^n (Z, \varnothing , !\varDelta )\).
-
\(n =0\): then the computation consists of the single state \((Z, \varnothing , !\varDelta )\), and \((Z,\varnothing ,!\varDelta ) \Downarrow Z\) is derivable by rule
 followed by as many applications of
followed by as many applications of  as the cardinality of \(\varDelta \).
as the cardinality of \(\varDelta \). -
\(n >0\): Let \(s \leadsto s'\) be the first transition of the computation. Let us call \(t_0\) the sub-computation of lenght \(n-1\) starting from \(s'\). We have the following three subcases, depending on the rule used to deduce \(s \leadsto s'\):
-
[\(\leadsto _{H}\)]. By definition, there exist X, Y, V such that \(s'= (Y \otimes V, \varGamma ', !\varDelta )\), \(W= X \otimes V\),
 and
and 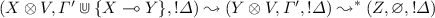 The induction hypothesis gives us \((Y \otimes V, \varGamma ', !\varDelta ) \Downarrow Z\), so we can build the following:
The induction hypothesis gives us \((Y \otimes V, \varGamma ', !\varDelta ) \Downarrow Z\), so we can build the following: 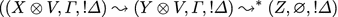
-
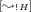 . By definition, there exist X, Y, V such that \(s'= (Y \otimes V, \varGamma , !\varDelta )\), \(W= X \otimes V\), \(X \multimap Y \in \varDelta \) and $$ ((X \otimes V, \varGamma , !\varDelta ) \overset{}{\leadsto } (Y \otimes V, \varGamma , !\varDelta ) \overset{}{\leadsto }^{*} (Z, \varnothing , !\varDelta ) $$
. By definition, there exist X, Y, V such that \(s'= (Y \otimes V, \varGamma , !\varDelta )\), \(W= X \otimes V\), \(X \multimap Y \in \varDelta \) and $$ ((X \otimes V, \varGamma , !\varDelta ) \overset{}{\leadsto } (Y \otimes V, \varGamma , !\varDelta ) \overset{}{\leadsto }^{*} (Z, \varnothing , !\varDelta ) $$The induction hypothesis gives us \((Y \otimes V, \varGamma , !\varDelta ) \Downarrow Z\), so we can build the following:
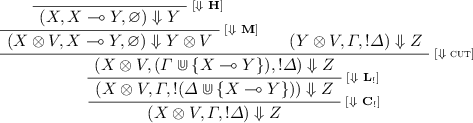
-
-
 . By definition, there exist V and an atom a such that \(s'= (1 \otimes V, \varGamma , !\varDelta )\), \(W= a \otimes a^{\perp } \otimes V\), and: $$ (a \otimes a^{\perp } \otimes V, \varGamma , !\varDelta ) \overset{}{\leadsto } (1 \otimes V, \varGamma , !\varDelta ) \overset{}{\leadsto }^{*} (Z, \varnothing , !\varDelta ) $$
. By definition, there exist V and an atom a such that \(s'= (1 \otimes V, \varGamma , !\varDelta )\), \(W= a \otimes a^{\perp } \otimes V\), and: $$ (a \otimes a^{\perp } \otimes V, \varGamma , !\varDelta ) \overset{}{\leadsto } (1 \otimes V, \varGamma , !\varDelta ) \overset{}{\leadsto }^{*} (Z, \varnothing , !\varDelta ) $$The induction hypothesis gives us \((1 \otimes V, \varGamma ', !\varDelta ) \Downarrow Z\), so we can build the following:
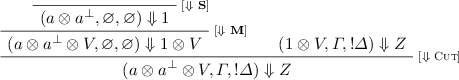
Theorem 3. Let \(\varOmega , \varGamma , !\varDelta \vdash Z\) be an honoured Horn sequent. Then:
Proof
Straightforward by Proposition 1 and Theorem 2. \(\square \)
1.3 A.3 Proofs for Sect. 4.3
Proposition 2. For all markings (m, d) of \(N = \mathcal {N}{({\varGamma _0,!\varDelta _0})}\) there exists a unique \(({W},{\varGamma })\) compatible with N such that \((m,d) = [{{W},{\varGamma }}]\).
Proof
We prove that \([{\cdot }]\) is injective and surjective over \((W, \varGamma )\) compatible with \(\mathcal {N}{({\varGamma _0,\varDelta _0})}\); the result then follows straightforwardly. Let us assume \((W_1,\varGamma _1) \ne (W_2,\varGamma _2)\); then either \(mset_{W_1}(s) \ne mset_{W_2}(s)\) for some \(s \in S^{atm}\), or \(\varGamma _1(in_0(s)) \ne \varGamma _2(in_0(s))\) for some \(s \in S^{ctrl}\), or \(mset_{W_1}(s^{\perp }) \ne mset_{W_2}(s^{\perp })\) for some \(s \in S^{atm}\); but then by compatibility and by definition of \([{\cdot }]\), \([{W_1,\varGamma _1}] \ne [{W_2,\varGamma _2}]\). This proves injectivity.
For surjectivity, if (m, d) is a marking of \(\mathcal {N}{({\varGamma _0,\varDelta _0})}\), we can build \((W,\varGamma )\) compatible with \(\mathcal {N}{({\varGamma _0,\varDelta _0})}\) s.t. \((m,d) = [{W,\varGamma }]\) as follows: to retrieve W we observe that m, d define a multiset M of occurences of literals as observed in Sect. 3; we take W to be the tensor product of all the elements of M. Let \(\varGamma \) comprise every implication \(s \in S^{ctrl}\) with multiplicity m(s). By construction, \(\langle {W} \rangle \subseteq S^{atm}\) and \(\varGamma \subseteq \varGamma _0\), so they are compatible with \(\mathcal {N}{({\varGamma _0,\varDelta _0})}\) and always by construction \((m,d) = [{W,\varGamma }]\). \(\square \)
Proposition 3. Let \(N = \mathcal {N}{({\varGamma _0,!\varDelta })}\), and let \((W,\varGamma )\) be compatible with N. Then:
Proof
From left to right we reason by cases, depending on the small-step rule we are using:
-
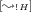 : then \(W= X \otimes V\), \(W'= Y \otimes V\), \(\varGamma = \varGamma '\) and
: then \(W= X \otimes V\), \(W'= Y \otimes V\), \(\varGamma = \varGamma '\) and 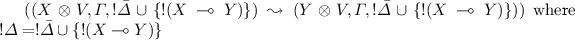 By Definition 8 we know that \([{W,\varGamma }]=(m,d)\) for some marking (m, d) such that for all \(s \in S^{atm}\) we have \(m(s) = mset_{W}(s) = mset_{X}(s) + mset_{V}(s)\) and \(r=in_1(X \multimap Y)\) for some transition r of N; then for all s, \(mset_{X}(s)=F(s,r)\) by Definition 7; since \(mset_{X}(s) + mset_{V}(s)= mset_{W}(s)= m(s)\), r is enabled in (m, d); moreover, for all s, we know by Definition 7 that \(mset_{Y}(s)=F(r,s)\) and \(mset_{Y}(s^{\perp })= L (s,r)\) so after firing r, \(mset_{W'}(s)=mset_{Y}(s) + mset_{V}(s)= m'(s)\) and \(mset_{Y}(s^{\perp }) + mset_{V}(s^{\perp })= d'(s)\) by Definition 7. Further \(m(s)=m'(s)\) when \(s \in S^{ctrl}\). Therefore, by Definition 8, then \([{W',\varGamma '}]=(m',d')\).
By Definition 8 we know that \([{W,\varGamma }]=(m,d)\) for some marking (m, d) such that for all \(s \in S^{atm}\) we have \(m(s) = mset_{W}(s) = mset_{X}(s) + mset_{V}(s)\) and \(r=in_1(X \multimap Y)\) for some transition r of N; then for all s, \(mset_{X}(s)=F(s,r)\) by Definition 7; since \(mset_{X}(s) + mset_{V}(s)= mset_{W}(s)= m(s)\), r is enabled in (m, d); moreover, for all s, we know by Definition 7 that \(mset_{Y}(s)=F(r,s)\) and \(mset_{Y}(s^{\perp })= L (s,r)\) so after firing r, \(mset_{W'}(s)=mset_{Y}(s) + mset_{V}(s)= m'(s)\) and \(mset_{Y}(s^{\perp }) + mset_{V}(s^{\perp })= d'(s)\) by Definition 7. Further \(m(s)=m'(s)\) when \(s \in S^{ctrl}\). Therefore, by Definition 8, then \([{W',\varGamma '}]=(m',d')\). -
 : then \(W= X \otimes V\), \(W'= Y \otimes V\),
: then \(W= X \otimes V\), \(W'= Y \otimes V\), 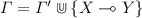 and
and 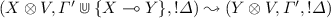 By Definition 8 we know that \([{W,\varGamma }]=(m,d)\) for some marking (m, d) such that for all \(s \in S^{atm}\) we have \(m(s) = mset_{W}(s) = mset_{X}(s) + mset_{V}(s)\) and \(r=in_0(X \multimap Y)\) for some transition r of N; then for all s, \(mset_{X}(s)=F(s,r)\) by Definition 7; since \(mset_{X}(s) + mset_{V}(s)= mset_{W}(s)= m(s)\), r is enabled in (m, d); moreover, for all s, we know by Definition 7 that \(mset_{Y}(s)=F(r,s)\) and \(mset_{Y}(s^{\perp })= L (s,r)\) so after firing r, \(mset_{W'}(s)=mset_{Y}(s) + mset_{V}(s)= m'(s)\) and \(mset_{Y}(s^{\perp }) + mset_{V}(s^{\perp })= d'(s)\) by Definition 7; moreover r has been fired in \((m',d')\) (so its control place has one fewer token). By Definition 8, then \([{W',\varGamma '}]=(m',d')\).
By Definition 8 we know that \([{W,\varGamma }]=(m,d)\) for some marking (m, d) such that for all \(s \in S^{atm}\) we have \(m(s) = mset_{W}(s) = mset_{X}(s) + mset_{V}(s)\) and \(r=in_0(X \multimap Y)\) for some transition r of N; then for all s, \(mset_{X}(s)=F(s,r)\) by Definition 7; since \(mset_{X}(s) + mset_{V}(s)= mset_{W}(s)= m(s)\), r is enabled in (m, d); moreover, for all s, we know by Definition 7 that \(mset_{Y}(s)=F(r,s)\) and \(mset_{Y}(s^{\perp })= L (s,r)\) so after firing r, \(mset_{W'}(s)=mset_{Y}(s) + mset_{V}(s)= m'(s)\) and \(mset_{Y}(s^{\perp }) + mset_{V}(s^{\perp })= d'(s)\) by Definition 7; moreover r has been fired in \((m',d')\) (so its control place has one fewer token). By Definition 8, then \([{W',\varGamma '}]=(m',d')\). -
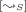 : then \(W= (a \otimes a^{\perp } ) \otimes V\), \(W'= 1 \otimes V\), \(\varGamma = \varGamma '\), and \( ((a \otimes a^{\perp } ) \otimes V, \varGamma , !\varDelta ) \leadsto (1 \otimes V, \varGamma , !\varDelta ) \)
: then \(W= (a \otimes a^{\perp } ) \otimes V\), \(W'= 1 \otimes V\), \(\varGamma = \varGamma '\), and \( ((a \otimes a^{\perp } ) \otimes V, \varGamma , !\varDelta ) \leadsto (1 \otimes V, \varGamma , !\varDelta ) \)
By Definition 8 we know that \([{W,\varGamma }]=(m,d)\) for some marking (m, d) such that for all \(s \in S^{atm}\) we have \(m(s) = mset_{W}(s)\); now since \(mset_{W}(a)\) and \(mset_{W}(a^{\perp }) >0\), \(m(a) > 0\) and \(d(a) > 0\), so annihilation is enabled at (m, d). After firing annihilation, we know that \(m'(a)= m(a)-1\) and \(d'(a)=d(a)-1\), while for all other \(s \ne a\), we have \(m'(s)= m(s)\) and \(d'(s)= d(s)\). Now it is easy to verify that \(mset_{W'}(a)= mset_{W}(a) -1\) and \(mset_{W'}(a^{\perp })= mset_{W}(a^{\perp }) -1\) and for all \(s\ne a\) \(mset_{W'}(s)= mset_{W}(s) \) (resp. \(mset_{W'}(s^{\perp })= mset_{W}(s^{\perp })\)). Control places are unaffected, so \(m(s) = m'(s)\) when \(s \in S^{ctrl}\). We conclude that \((m',d')= [{W', \varGamma '}]\).
From right to left we reason by cases, depending on the type of step:
-
Suppose we fire \(r = in_i(X \multimap Y)\) at \((m,d)=[{W,\varGamma }]\). We know that \((m,d) \xrightarrow {} (m',d')\) by firing r for some \(m', d'\) and \((m',d')= [{W',\varGamma '}]\) for some \(W',\varGamma '\) by Proposition 2; since r is enabled in (m, d), for all \(s\in S^{atm}\) such that \(mset_{X}(s)\ge 0\), we have that \(m(s) \ge mset_{X}(s)\) and since \((m,d)=[{W, \varGamma }]\), we have that \(mset_{W}(s) \ge mset_{X}(s) \). This means that, \(W= X \otimes V\) for some V (so when \(s \in S^{atm}\) we have \(m(s)= mset_{X}(s) + mset_{V}(s)\) and \(d(s)= mset_{X}(s^{\perp }) + mset_{V}(s^{\perp })\)). Now we have two subcases:
-
if \(i=1\), then for all \(s \in S^{ctrl}\), \(m(s)= m'(s)\) so, since \((m,d) =[{W,\varGamma }]\) and \((m',d') =[{W',\varGamma '}]\), \(\varGamma = \varGamma '\); moreover for all \(s \in S^{atm}\), \(m'(s)= mset_{Y}(s) + mset_{V}(s)\) and \(d'(s)= mset_{Y}(s^{\perp }) + mset_{V}(s^{\perp })\) (by definition of \(\xrightarrow {}\), and Definition8). But then, \(W'= Y \otimes V\) and \( ( (X \otimes V, \varGamma , !\varDelta \cup \{!(X \multimap Y)\}) \leadsto (Y \otimes V, \varGamma , !\varDelta \cup \{!(X \multimap Y)\}) )\)
-
otherwise, \(i = 0\) which implies \((m,d)= [{W,\varGamma }]\) and \((m',d')= [{W',\varGamma '}]\), with \(\varGamma ' = \varGamma \setminus \{X \multimap Y \} \). Moreover \(m'(s)= mset_{Y}(s) + mset_{V}(s)\) and \(d'(s)= mset_{Y}(s^{\perp }) + mset_{V}(s^{\perp })\) (by definition of \(\xrightarrow {}\), and Definition 8). But then \(W'= Y \otimes V\) and \( (X \otimes V, \varGamma , !\varDelta ) \leadsto (Y \otimes V, \varGamma ', !\varDelta ) \)
-
-
annihilation is enabled in \((m,d)= [{W,\varGamma }]\). We know that \((m,d) \xrightarrow {} (m',d')\) through an annihilation step and \((m',d')= [{W',\varGamma '}]\) for some \(W',\varGamma '\) by Proposition 2. Since an annihilation is enabled, for some atom a, \(m(a) \ge 1, d(a) \ge 1\); now for all s, \(m(s) = mset_{W}(s)\), and \(d(s)=mset_{W}(s^{\perp })\), so for some a, V, \(W= (a \otimes a^{\perp }) \otimes V\). Then \((W,\varGamma , !\varDelta )\leadsto (1 \otimes V, \varGamma ', !\varDelta )\) (where \(\varGamma =\varGamma '\)). It remains to prove that \(W'= 1 \otimes V\); this follows from the fact that for \(s= a\), \(m'(s)= mset_{W}(s) -1\) and \(d'(s)= mset_{W}(s^{\perp }) -1\) (by definition of \(\xrightarrow {}\), and Definition 8). \(\square \)
Theorem 4. Let \(N = \mathcal {N}{({\varGamma , !\varDelta })}\). An honoured Horn sequent \(\varOmega , \varGamma , ! \varDelta \vdash Z\) of \({\text {ILL}}^{mix}\) is provable iff \([{\bigotimes \varOmega ,\varGamma }] \xrightarrow {}_{N}^* [{Z,\varnothing }]\).
Proof
By Theorem 3, we know that \(\varOmega , \varGamma , ! \varDelta \vdash Z\) is provable if and only if \((\bigotimes \varOmega , \varGamma , !\varDelta ) \leadsto ^{*} (Z, \emptyset , !\varDelta )\). By Proposition 3, \((\bigotimes \varOmega ,\varGamma , !\varDelta )\leadsto ^{*} (Z, \emptyset , !\varDelta )\) iff \([{\bigotimes \varOmega ,\varGamma }] \xrightarrow {}_{N}^* [{Z, \emptyset }]\). \(\square \)
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Bartoletti, M., Degano, P., Di Giamberardino, P., Zunino, R. (2015). Debits and Credits in Petri Nets and Linear Logic. In: Martí-Oliet, N., Ölveczky, P., Talcott, C. (eds) Logic, Rewriting, and Concurrency. Lecture Notes in Computer Science(), vol 9200. Springer, Cham. https://doi.org/10.1007/978-3-319-23165-5_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-23165-5_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-23164-8
Online ISBN: 978-3-319-23165-5
eBook Packages: Computer ScienceComputer Science (R0)


 ,
,  ,
,  ,
,  , or
, or  . Straightfoward.
. Straightfoward. . We have:
. We have: 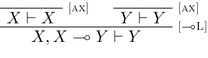
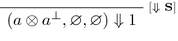
 . We have:
. We have: 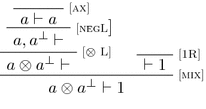
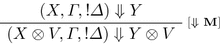
 . We have:
. We have: 
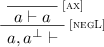
 ,
,  ,
, 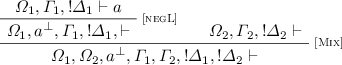
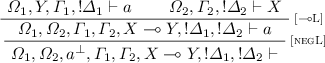
 . We have:
. We have: 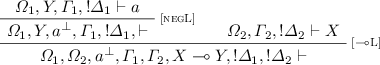
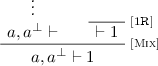
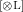 ,
,  ,
,  ,
,  ,
, 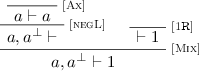
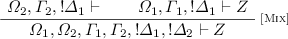
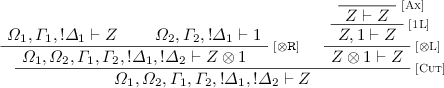
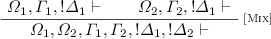
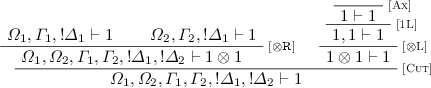
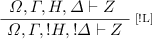
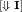 .
.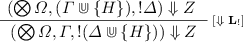
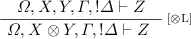
 . We have:
. We have: 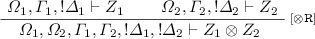
 . The thesis follows because
. The thesis follows because  .
.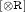 . We have:
. We have: 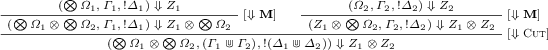
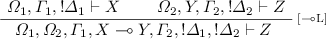
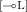 . We have:
. We have: 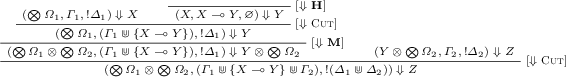
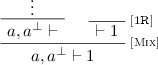
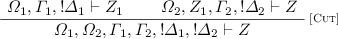
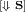 .
.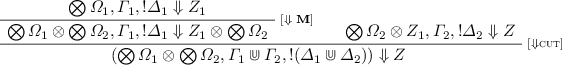
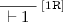
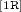 . We have:
. We have: 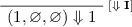
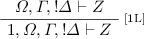
 . We have:
. We have: 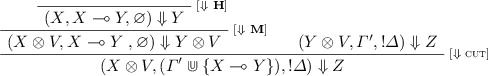
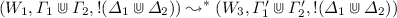 .
.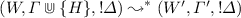 where H is a Horn implication, then
where H is a Horn implication, then 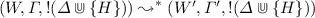 .
. .
. where H is a Horn implication, then
where H is a Horn implication, then  .
.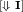 . By reflexivity of
. By reflexivity of  . By rule
. By rule 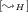 ,
, 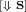 . By rule
. By rule  ,
,  . By applying the induction hypothesis on both premises, we obtain:
. By applying the induction hypothesis on both premises, we obtain: 
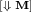 . By the induction hypothesis and item (2) of Lemma
. By the induction hypothesis and item (2) of Lemma 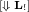 . By the induction hypothesis and item (3) of Lemma
. By the induction hypothesis and item (3) of Lemma  . By the induction hypothesis and item (4) of Lemma
. By the induction hypothesis and item (4) of Lemma 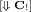 . By the induction hypothesis and item (5) of Lemma
. By the induction hypothesis and item (5) of Lemma  followed by as many applications of
followed by as many applications of  as the cardinality of
as the cardinality of  and
and 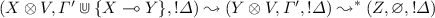 The induction hypothesis gives us
The induction hypothesis gives us 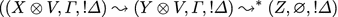
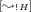 . By definition, there exist X, Y, V such that
. By definition, there exist X, Y, V such that 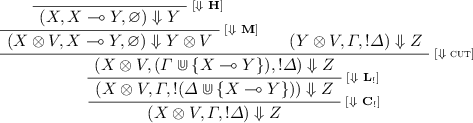
 . By definition, there exist V and an atom a such that
. By definition, there exist V and an atom a such that 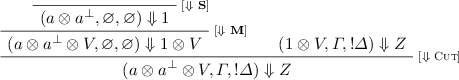
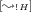 : then
: then 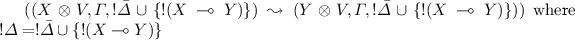 By Definition
By Definition  : then
: then 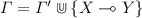 and
and 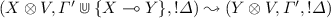 By Definition
By Definition  : then
: then