Abstract
In this chapter a general strategy for constructing modal theories is developed. The idea is to state the modal principles, known from modal operator logic, in the predicate setting by appeal to the truth predicate. Thereby one can block the introduction and elimination of sentential predicates, which is the principal source of paradox. The strategy is used to construct two modal theories, MFS and MKF, over the axiomatic theories of truth FS and KF respectively. Both theories are supplied with a new kind of semantics. It is also shown that the modal predicates of the two theories can be understood along the lines of a proposal by Kripke, namely, as a truth predicate modified by an appropriate modal operator.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The present chapter overlaps substantially with the content published in Stern [157, 158].
- 2.
The idea of connecting the view we have outlined to deflationism was suggested to us by Martin Fischer.
- 3.
In Stern [157, 158] the rule \((T\text{- }Nec)\) was formulated in a slightly weaker way:
$$\begin{aligned}\frac{T\lceil \phi \rceil }{N\lceil \phi \rceil },\phi \in Sent_{\mathcal {L}_{PATN}}. \end{aligned}$$The present formulation is preferable because it is unclear whether Theorems 4.8 and 4.45 can be proved using the weaker formulation of \((T\text{- }Nec)\).
- 4.
Koellner [86] uses a similar strategy in developing the theory DTK , which is a theory of truth and absolute provability.
- 5.
This should be clear from the discussion in the last two chapters, but see Leitgeb [97] for a list of desiderata a theory of truth should fulfill but cannot.
- 6.
This excludes prominent axiomatic theories like Cantini’s VF we have briefly discussed in the previous chapter (cf. Cantini [24, 25]).
- 7.
Cf. Halbach and Welch [68] for an understanding of Kripke’s proposal along these lines.
- 8.
See Kripke [91], p. 713/714.
- 9.
A similar reduction has recently been carried out by Halbach and Welch [68]. Yet, Halbach and Welch’s investigation is purely semantic in character, as they show the translation to preserve truth between two intended semantics.
- 10.
More precisely, in the terminology of Fischer et al. [44] both theories are \(\mathbb {N}\) -categorical axiomatizations of their respective semantics. We will explain both adequacy results in some detail later in this chapter.
- 11.
When we speak of axioms in the extended language we assume that the syntactic predicates have been extended to the new language. We also allow formulas of the extended languages to appear in the induction scheme.
- 12.
For an exposition of the recursion theorem see, e.g., Rogers [142] or Monk [110].
- 13.
The technique just hinted at is sketched out in some detail in the proof of Theorem 4.19.
- 14.
At this point it is crucial to appreciate that the numeral of the Gödel number of the value of a name need not be the name itself.
- 15.
In this derivation we cannot replace the use of Fact 4.3 by an application of \((T\text{- }Intro)\) because \(\chi \) is an open formula and not a sentence of the language. This explains the restriction to arithmetic formulas in Lemma 4.9. The schematic version of (ii) and (iii) for sentences \(\phi \) and \(\psi \) holds unrestrictedly.
- 16.
The necessitation of open formulas is actually more involved than simply applying the rule \((Nec_N)\), which is restricted to sentences: suppose we have derived \(\phi (x)\). Then by generalization we obtain \(\forall x\phi (x)\) and by \((Nec_N)\) \(N\lceil \forall x\phi (x)\rceil \). But by Lemma 4.9 and universal instantiation this yields \(N\lceil \phi (\dot{x})\rceil \). In light of these remarks we shall apply \((Nec_N)\) to open formulas.
- 17.
As we have set up things there is no de re modality in the predicate approach. Quine [136] and, Belnap and Gupta [14] (cf. 237/38) suggest treating the modal predicate as a two place predicate applying to the code of a formula and the code of a sequence of objects (thus similar to a satisfaction predicate) in order to recover de re reading in this context. See also Halbach and Welch [68] and our introduction for remarks to this effect.
- 18.
All formation rules are standard, that is, no restriction on the formation rules as in the case of \(\mathcal {L}_{PA}^{\Box \blacksquare }\) are in place. For this reason we have omitted giving a full fledged definition of the language.
- 19.
\(FS\Box \) is consistent in all consistent normal modal logics. If the normal modal logic is a sublogic of the identity logic, we may give an interpretation of \(FS\Box \) in FS by translating \(\Box \phi \) by \(\phi \). If \(\phi \) is a sublogic of the unit logic, we may uniformly translate a formula \(\Box \phi \) by \(s=s\) for some term s.
- 20.
Actually, \((ND\Box )\) and \((BF\Box )\) are derivable in S5 iff standard first-order logic is assumed and the language includes an identity symbol—this latter point is non trivial in the case of the Barcan formula (cf. Corsi [30]). See Fitting and Mendelsohn [46] for proofs of these facts. We have nonetheless decided to explicitly mention \((ND\Box )\) and \((BF\Box )\), as these are the only additional principles we need to add to the smallest normal modal logic K iff we wish to reduce BMFS to \(FS\Box \). But in K, assuming standard first-order logic, neither \((ND\Box )\) nor \((BF\Box )\) are derivable.
- 21.
As a matter of fact, the same applies to the translation function g of Theorem 4.5.
- 22.
The Converse Barcan formula

is derivable in any normal extension of K, if standard first-order logic is assumed.
- 23.
See also Belnap and Gupta [14] for a detailed presentation and discussion of the revision theory of truth.
- 24.
Semantic theories of truth and possible world semantics have been combined by several authors in constructing a semantics for modal predicates. See, e.g., Asher and Kamp [11], Belnap and Gupta [14], Halbach et al. [67], Leitgeb [95] and, Halbach and Welch [68]. Asher and Kamp , Belnap and Gupta, and Halbach et al. also work in the setting of the revision theory of truth, though our approach is somewhat different.
- 25.
We assume \(\bigcap \) to be an operation on \(P(\omega )\). Thus in particular if \([wR]=\emptyset \), then \(\bigcap _{v\in [wR]}f(v)=\omega \).
- 26.
\(\Gamma ^\omega _f[Val_F]\) is defined as \(\bigcap _{n\in \omega }\Gamma ^n_F[Val_F]\).
- 27.
Since we are working in the standard model we only need to be concerned with standard sentences.
- 28.
\(t^{\mathbb {N}}\) stands for the denotation (the value) of t in the natural number structure.
- 29.
Cf. Halbach [66], pp. 197/198. Halbach shows something slightly stronger, namely, that (FS2) and (KF8) are inconsistent with PAT but his result relies on the fact that the strong Diagonal lemma is provable (which is the case for PAT as defined by Halbach). Otherwise, (FS2) and (KF8) are jointly consistent in PAT. We don’t know whether the inconsistency of (FS2) with \({ {KF}}\) can be derived in languages lacking the necessary function symbols, that is, assuming an underlying arithmetical theory that does not prove the strong Diagonal lemma. See Heck [69] for more on this.
- 30.
Conversely, we may also consistently add the converse direction to \({ {KF}}\), that is, the completeness axiom
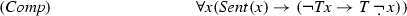
as long as we do not add (Cons).
- 31.
The notion of groundedness and the notion of a total and consistent formula are not to be equated. The example was meant to be nothing but an analogy, which we hope to be helpful for the reader.
- 32.
Again this derivation relies on the fact that we can prove the strong Diagonal lemma in PATN. We don’t know whether this result obtains in the broader setting.
- 33.
Note that in BMKF we may prove \((Reg_{T})\) by an induction over the positive complexity of a formula. It is not guaranteed that \((Reg_{T})\) is a theorem of any modal extension of \({ {KF}}\).
- 34.
Basically our construction is a variant of the construction of Halbach and Welch [68].
- 35.
Again \(\bigcap \) is taken to be an operation on \(P(\omega )\).
- 36.
For the next two axioms we consider only the case in which we have Sent(Val(t)). The other case is trivial.
- 37.
Applying the same reasoning we used in the case of \(FS\Box \) we may show \(KFC\Box \) to be consistent.
- 38.
Maybe adopting a rule of proof such as
$$\begin{aligned}\frac{\forall x,y(Sent(x)\wedge Sent(y)\rightarrow (Tx\leftrightarrow Ty))}{\forall x,y(Sent(x)\wedge Sent(y)\rightarrow (Px\leftrightarrow Py))}\end{aligned}$$would be of some help here.
- 39.
The findings in Stern [161] where a very similar strategy is applied to the non-classical theory PKF confirm this assessment.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Stern, J. (2016). Modality and Axiomatic Theories of Truth. In: Toward Predicate Approaches to Modality. Trends in Logic, vol 44. Springer, Cham. https://doi.org/10.1007/978-3-319-22557-9_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-22557-9_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-22556-2
Online ISBN: 978-3-319-22557-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)