Abstract
In this chapter we give a concise review of the quantum mechanics formalism from a perspective which generalizes the ordinary Schroedinger formulation. In this way we may reconsider the Schroedinger approach to quantum mechanics from a more geometrical and group-theoretical point of view and show the close relationship between the classical Hamiltonian theory and quantum mechanics. Moreover the formalism developed in this chapter will be useful for an appropriate exposition of the relativistic wave equations in Chap. 10 and the field quantization approach in Chap. 11.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
We recall that a Cauchy sequence is any sequence of elements \(\phi _n\) such that \(\lim _{m,n\rightarrow \infty } d(\phi _n,\phi _m)=0\). In particular, the finite dimensional space \(V_n^{(c)}\) treated so far is trivially a Hilbert space.
- 2.
Indeed the expansion (9.14) is quite analogous to the expansion of an ordinary vector \(\mathbf {v}\) along a orthonormal basis \(\mathbf {u}_i\) in a finite dimensional space
$$\begin{aligned} \mathbf {v}= \sum _i v^i\mathbf {u}_i=\sum _i \mathbf {u}_i (\mathbf {u}_i\cdot \mathbf {v}) \end{aligned}$$and the “wave function” representation \(\{\langle F| v \rangle \}\) of \(\mathbf{v}\) corresponds to the representation of the vector in terms of its components along the chosen basis: \(\mathbf{v}\equiv \{v^i\}\).
- 3.
As we shall see in Sect. 9.3.1, when dealing with free one-particle states, we can avoid the use of non-normalizable wave functions, generalized functions Dirac delta-functions etc., by quantizing the physical system in a box. In this case, instead of considering the whole \({\mathbb R}^3\) as the domain of integration, we take a large box of finite volume V, so that the functions which were not \(L^2(-\infty ;+\infty )\)-integrable become now \(L^2(V)\)-integrable. In this way we may always restrict ourselves to considering the Hilbert space of functions defined over a finite volume.
- 4.
This is not an uncommon feature. For example in the Fourier integral transform
$$ f(x)=\frac{1}{\sqrt{2\pi }}\int dp \,F(p) \, e^{ipx}, $$if \(f(x)\subset L^2(-\infty ;+\infty )\), so does its Fourier transform. However the basis functions \(\frac{1}{\sqrt{2\pi }}e^{ipx}\) are not in \(L^2(-\infty ;+\infty )\) since \(|\frac{1}{\sqrt{2\pi }}e^{ipx}|^2=\frac{1}{{2\pi }}\).
- 5.
As we shall see in Chap. 11 a consistent interpretation of a quantum relativistic theory requires that the interpretation of \(\varPhi _{(a)}(\mathbf {x})\) as a quantum mechanical wave function must be abandoned and that the classical field be promoted to a quantum mechanical operator.
- 6.
Clearly a normalization factor should be used when giving this interpretation since \(A_\mu \) has dimension \((Newton)^{\frac{1}{2}}\) and not \((length)^{\frac{3}{2}}\), as a wave.
- 7.
We warn the reader that, in the case of space-time transformations, the orthonormal basis \(|{ \mathbf {u}_i}\rangle \) has nothing to do with the space, or space-time, reference frame which undergoes the transformation.
- 8.
An antiunitary operator \(\hat{A}\) does not fit the definition of linear operators given in Eq. (9.7). In fact \(\hat{A}\) is an example of an antilinear operator defined by the property
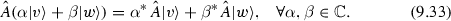
- 9.
Note that the imaginary unit i in Eq (9.34) has been inserted in order to deal with hermitian generators.
- 10.
We have also used the property of delta-functions \(\delta (cx)=\delta (x)/c\), so that \(\delta ^3(\mathbf{k}-\mathbf{k}')=\hbar ^3\,\delta ^3(\mathbf{p}-\mathbf{p}')\).
- 11.
In fact we shall characterize a single particle state as belonging to an irreducible representation of the Poincaré group.
- 12.
This statement seems to be at odds with what we have learned from our earlier discussion about Lorentz transformations: Under a Lorentz transformation a generic position four-vector \(x^\mu \) transforms into a different one \(x'^\mu =\varLambda ^\mu {}_\nu \,x^\nu \), and the only four vector which is left invariant is the null one \((x^\mu )\equiv \mathbf{0}=(0,0,0,0)\) defining the origin O of the RF. For a given Lorentz transformation \(\varvec{\Lambda }\) in \(\mathrm{SO}(1,3)\) and a point P described by \(x\equiv (x^\mu )\), we can define the Poincaré transformation \(\varLambda _x\equiv (\mathbf{1},-x)\,(\varvec{\Lambda },0)\,(\mathbf{1},x)\), see Sect. 4.7.2 of Chap. 4 for the notation, which consists in a first translation \((\mathbf{1},x)\) mapping P into the origin O (\(x\rightarrow \mathbf{0}\)), then a Lorentz transformation \(\varvec{\Lambda }\) which leaves O invariant (\( \mathbf{0}\rightarrow \mathbf{0}\)), followed by a second translation which brings O back into P (\( \mathbf{0}\rightarrow x\)). By construction \(\varLambda _x\), which is not pure Lorentz since it contains translations, leaves x invariant. The transformations \(\varLambda _x\), corresponding to \(\varvec{\Lambda }\in \mathrm{SO}(1,3)\), close a group which has the same structure as the Lorentz group, though being implemented by different transformations: The correspondence \(\varvec{\Lambda }\leftrightarrow \varLambda _x\) for a given x is one-to-one, and, moreover, if \(\varvec{\Lambda }\varvec{\Lambda }'=\varvec{\Lambda }''\) then \(\varLambda _x\varLambda '_x=\varLambda ''_x\). The two groups are said to be isomorphic. Transformation groups sharing the same structure represent the same symmetry. We shall denote the group consisting of the \(\varLambda _x\) transformation by \(\mathrm{SO}(1,3)_x\). It can be regarded as the copy of the Lorentz group, depending on the point x, which leaves x invariant.
- 13.
A problem related to the non-unitarity of \(\mathbf{D}\) is the fact that if we defined \(\varPhi ^\alpha (x)=\langle x ,\alpha |a\rangle \), as we did in the non-relativistic theory, it would no longer have the correct transformation property (9.99) under Poincaré transformations. For spin 1 / 2 and 1 particles, we can however define a real symmetric matrix \(\varvec{\gamma }=(\gamma _{\alpha \beta })\) squaring to the identity \(\varvec{\gamma }^2=\mathbf{1}\), such that \(\varvec{\gamma }\,\mathbf{D}(\varvec{\Lambda })^\dagger \,\varvec{\gamma }=\mathbf{D}(\varvec{\Lambda })^{-1}\): For spin 1 particles \(\mathbf{D}\) is the fundamental representation, namely \(\mathbf{D}(\varvec{\Lambda })=\varvec{\Lambda }\), and \(\varvec{\gamma }=\varvec{\eta }\), while for spin 1 / 2 particles, as it will be shown in next chapter, \(\mathbf{D}\) is the spinorial representation and \(\varvec{\gamma }=\gamma ^0\). We can use this matrix to define \(\varPhi ^\alpha (x)\equiv \langle x ,\beta |a\rangle \,\gamma ^{\alpha \beta }\). We shall however, for notational convenience, still write \(\varPhi ^\alpha (x)=\langle x ,\alpha |a\rangle \), keeping though this subtlety in mind. We can also use the \(\varvec{\gamma }\) matrix to define a Lorentz-invariant normalization for the \(|x,\alpha \rangle \) states: \(\langle x,\alpha |x',\beta \rangle =\delta ^4(x'-x)\,\gamma _{\alpha \beta }\). Such normalization is however problematic since \(\varvec{\gamma }\) is not positive definite and thus some of these states would have negative norm!
- 14.
If we consider proper Lorentz transformations (\(\varLambda ^0{}_0\ge 0,\,\mathrm{det}\varvec{\Lambda }=1\)), the sign of \(p^0\), eigenvalue of \(\hat{P}^0\), is invariant as well.
- 15.
Here we are restricting to proper Lorentz transformations. The parity transformation \(\varvec{\Lambda }_P:\,\,p^0\rightarrow p^0,\,\mathbf{p}\rightarrow -\mathbf{p}\) reverses the sign of \(\varGamma \).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this chapter
Cite this chapter
D’Auria, R., Trigiante, M. (2016). Quantum Mechanics Formalism. In: From Special Relativity to Feynman Diagrams. UNITEXT for Physics. Springer, Cham. https://doi.org/10.1007/978-3-319-22014-7_9
Download citation
DOI: https://doi.org/10.1007/978-3-319-22014-7_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-22013-0
Online ISBN: 978-3-319-22014-7
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)