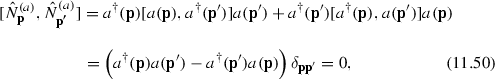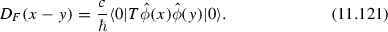Abstract
In the previous chapter we have examined the relativistic wave equations for spin 0 and spin 1/2 particles. The corresponding fields \(\phi (x)\) and \(\psi ^\alpha (x)\) were classical in the same sense that the Schroedinger wave function \(\psi (\mathbf {x},t)\) is a classical field. In contrast to the non-relativistic Schroedinger construction, we have seen that requiring relativistic invariance of the quantum theory, that is invariance under Poincaré transformations, unavoidably leads to serious difficulties when trying to interpret the field as representing the physical state of the system: It implies the appearance of a non-conserved probability density and, most of all, the appearance of negative energy states. Note that the latter difficulty is in some sense contradictory because if we just consider the field aspect of the wave equations, the field energy, expressed in terms of the canonical energy momentum tensor, is positive.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
In this chapter we denote the Poisson brackets by the symbol \(\{,\}_{P.B.}\) since we want to reserve the symbol \(\{A,B\}\) to the anticommutator of quantum operators, \(\{A,B\}=AB+BA\).
- 2.
Actually we shall only consider the quantum description of the interaction between the electromagnetic field and a Dirac field.
- 3.
We have used a similar argument after Eq. (10.30), in the classical case.
- 4.
In the discrete notation we shall often use the following symbols \(a_\mathbf{p}\equiv a(\mathbf{p}),\,b_\mathbf{p}\equiv b(\mathbf{p})\).
- 5.
The fact that \([\hat{N}^{(a)},\,\hat{N}^{(b)}]=0\) immediately follows from the property that a and b commute, as stressed after (11.33). Consider now the number operators corresponding to oscillators of a given kind, say (a):
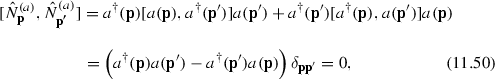
the same result obviously holds for the operators \(\hat{N}^{(b)}\).
- 6.
In the above derivation we have used the Lorentz invariance of the measure \(d^3\mathbf {p} V\) and of \(E_\mathbf{p} V\), see Sect. 9.5 of Chap. 9.
- 7.
The intrinsic parity can only be fixed by experiment involving interactions, so that it is meaningful only when specified relative to other particles.
- 8.
Since the parity transformation is involutive, \(U(P)^2=\hat{I}\), its eigenvalues can only be \(\pm 1\).
- 9.
For a formal treatment of this issue see for instance A. Messiah, Quantum Mechanics, Dover 1999.
- 10.
Let us repeat here the argument given in Chap. 4 in a more compact form. Suppose \(p^0> 0\), in a frame S. In a Lorentz transformed frame \(S'\) moving at velocity \(\mathbf{v}\) relative to S, we have
$$ p'^{0}=\gamma \left( p^0-\frac{\mathbf {v}}{c}\cdot \mathbf {p}\right) \ge \gamma \left( p^0-\frac{|\mathbf {v}|}{c} \mathbf {|p|}\right) . $$However \(p^0=\sqrt{\mathbf {|p|^2}+m^2c^2}\ge |\mathbf {p}|\) and therefore, since \(\frac{\mathbf {|v|}}{c}< 1\)
$$ p'^{0}\ge \gamma \left( 1-\frac{\mathbf {|v|}}{c}\right) \mathbf {|p|}> 0. $$ - 11.
We note that the requirement of causality refers to observables and in general field operators are not necessarily observables. However quite generally observables in a physical system are constructed in terms of local functions of the field variables so that the requirement of causality can be expressed in terms of the fields themselves. The requirement of commuting operators for space-like separations is also called “locality” and, correspondingly, the quantum field theory is referred to as a “local theory”. Locality assures that the results of two measures made at a space-like distance cannot have any influence on one another, there being no correlation between the two events.
- 12.
For a hermitian (and thus neutral) field
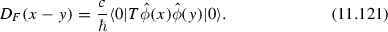
- 13.
This property is easily proven on a generic test function f(z): \(\int _{-\infty }^\infty f(z) \frac{d}{dz}\theta (z)dz=-\int _{-\infty }^\infty f'(z) \theta (z)dz=-\int _{0}^\infty f'(z)dz=f(0)=\int _{-\infty }^\infty f(z) \delta (z)dz\).
- 14.
In this subsection we restore the “hat” symbol on the field operators.
- 15.
We suppress here and in the following the “hat” symbol for the field operator.
- 16.
To prove it suffices to note that \(\mathbf{S}(T)p\!\!\!/\mathbf{S}(T)^{-1}=\gamma ^{\mu \,*}p'_{\mu }\), where \((p'^\mu )\equiv (p^0,\,-\mathbf{p})\) and that \(\mathbf{S}(T)u(\mathbf{0},r)=\epsilon _{rs}\,u(\mathbf{0},s)\).
- 17.
Here and in the remainder of this chapter we denote the quantized fields without the “hat symbol”.
- 18.
It is straightforward to prove this property in a generic RF, using the general expression of \(L(\mathbf{k})\) in Eq. (11.252)
$$\begin{aligned}{}[L(\mathbf{k}),L(\mathbf{k}')^\dagger ]= & {} k^\mu k'^\nu \varepsilon ^{(\lambda )}_{\mathbf{k},\mu }\varepsilon ^{(\sigma )}_{\mathbf{k}',\nu }\,[a_{\mathbf{k}\,\lambda },\,a^\dagger _{\mathbf{k}'\,\sigma }]\nonumber \\ {}= & {} -k^\mu k'^\nu \varepsilon ^{(\lambda )}_{\mathbf{k},\mu }\varepsilon ^{(\sigma )}_{\mathbf{k}',\nu }\eta _{\lambda \sigma }\,\delta _{\mathbf{k}\,\mathbf{k}'}=-k^2\,\delta _{\mathbf{k}\,\mathbf{k}'}=0, \end{aligned}$$(11.257)where we have used the photon mass-shell condition \(k^2=0\) and the completeness property of the polarization vectors.
- 19.
Note that this correspondence should take into account a normalization factor due to the fact that \(A_\mu (x)\) does not have the dimension of a wave-function: \(\langle \mathbf{x}| s_0\rangle \).
- 20.
In Chap. 6 the direction of motion was chosen along the X-axis so that the transverse directions were 2 and 3. Here the motion is chosen along the Z axis.
- 21.
As often done previously, we shall omit in this section the hat symbol on field operators only.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this chapter
Cite this chapter
D’Auria, R., Trigiante, M. (2016). Quantization of Boson and Fermion Fields. In: From Special Relativity to Feynman Diagrams. UNITEXT for Physics. Springer, Cham. https://doi.org/10.1007/978-3-319-22014-7_11
Download citation
DOI: https://doi.org/10.1007/978-3-319-22014-7_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-22013-0
Online ISBN: 978-3-319-22014-7
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)