3D Shapes Isometric Deformation Using in-tSNE

Abstract

Isometric shapes share the same geometric structure, and all possible bendings of a given surface are considered to have the same isometric deformation. Therefore, we use the inner distance to describe the isometric geometric structure. The inner distance is defined as the length of the shortest path between landmark points with the bending stability. Stochastic neighbor embedding algorithm t-SNE is a manifold embedding algorithm to visualize high-dimensional data by giving each data point a location in a two or three-dimensional map. Then, t-SNE is applied to 3D shapes isometric deformation in which Euclidean distances in high-dimensional space are replaced by inner distances. We can use this isometric deformation to describe invariant Signatures of surfaces, so that the matching of nonrigid shapes is better.

1 Introduction

With the development of 3D acquisition techniques, 3D mesh models are now widely available and used in computer vision, computer graphics, and pattern recognition. Thus, the demand for model analysis and understanding is ever increasing. However, automatic matching of nonrigid surfaces is a challenging problem. We believe nonrigid surfaces are isometric, and share the same geometric structure [1]. Therefore, we can research the isometric deformation of nonrigid surfaces based on manifold embedding algorithms, in order to realize the automatic matching of the blending shapes. This paper presents a method In-tSNE based on the t-SNE [2] in which high-dimensional Euclidean distance is replaced by inner distance [3], to realize the isometric deformation of 3D shapes.

The outline of this paper is as follows. Introduction and related work are presented in Sects. 1 and 2. The inner distance is introduced in Sect. 3. Section 4 reviews stochastic neighbor embedding algorithm and t-SNE. Subsequently, key points extraction and In-tSNE presented in Sect. 5. Experimental results and conclusion are shown in Sects. 6 and 7.

2 Related Work

Manifold embedding methods are divided into global and local embedding. Tenenbaum et al. proposed a global Isometric Feature Mapping (Isomap) [4], which can truly reflect the global structure of the data. Roweis and Saul proposed LLE [5] feature mapping algorithm which focuses on ensuring the local structure, and the local geometric structure is close to the Euclidean space. SNE [6] is a probabilistic approach, and it starts by converting high-dimensional distance or similarity data into a set of conditional probabilities under Gaussian distribution. Then, t-SNE is a variation of SNE. And t-SNE uses a Student-t distribution rather than a Gaussian to compute the similarity between two points in the low-dimensional space.

Now, the matching of 3D shapes has made great progress, but most of the matching algorithms are unable to handle the nonrigid shapes like articulated object. Therefore, Schwartz [7] proposed using the isometric embedding approach to fatten a cortical triangulated surface onto a plane. Elad and Kimmel [1] proposed embedding surfaces into a higher-dimensional Euclidean space in order to compute their isometric invariant signatures. This paper applies t-SNE to the 3D shapes isometric deformation in which Euclidean distances in high-dimensional space are replaced by inner distance.

3 Inner Distance

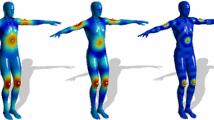
The inner distance is very similar to the geodesic distance on surfaces. Both of them have the certain bending stability. Euclidean distance doesn’t have the bending stability. Geodesic distance is defined as the shortest path along the shape surface, and the inner distance is defined as the shortest path along the inside of the body (Fig. 1).

Fig. 1.

Comparison of inner distance and geodesic distance. Red solid line represents the shortest path of the geodesic distance, and the red dashed line is the shortest path of the inner distance. As can be seen, the inner distance can be a good description of the shape. (Color figure online)

We transform a triangle mesh into a voxel representation [8], and construct an undirected graph using voxel. Each node in the graph represents a voxel unit. So, the inner distance is the length of the shortest path between landmark points. Here, we use Dijkstra algorithm to compute the shortest path. The time complexity of the algorithm is reduced to NlogN by optimization of stack (Fig. 2).

Fig. 2.

Inner distance of 3D shape based on voxel. The left is the original shape, the middle body is a voxelized model, and the right is the shortest path of inner distance between point A and point B.

4 Stochastic Neighbor Embedding Algorithm

4.1 Stochastic Neighbor Embedding

SNE is a probabilistic approach of manifold embedding to the task of placing objects, described by high-dimensional vectors or by pairwise similarities, in a low-dimensional space in a way that preserves neighbor identities. According to SNE, the distance of data set is the reflection of the absolute distance between pairwise data, while manifold embedding algorithm is easier to profit from the relative distance between pairwise data. Therefore, SNE abandoned the absolute distance measurement instead of using the probability of one data point randomly selecting another data point as its nearest neighbor to describe pairwise similarities. The similarity is modeled as a probability of random neighbor selection based on Gaussian neighborhoods. The aim of the embedding is to approximate this distribution as well as possible when the same operation is performed on the low-dimensional space. The similarity of data point x_j to data point x_i is the conditional probability, p_j|i, that x_i would pick x_j as its neighbor if neighbors were picked in proportion to their probability density under a Gaussian centered at x_i.

Mathematically, the conditional probability by Gaussian neighborhoods in high-dimensional space:

$$ P_{j/i} = \frac{{\exp ( - \,||\,x_{i} - x_{j} \,||^{2} \,/\,2\upsigma^{2} )}}{{\sum\limits_{k \ne i} {\exp ( - \,||\,x_{i} - x_{k} \,||^{2} \,/\,2\upsigma^{2} )} }} $$

(1)

In the low-dimensional space, we also use Gaussian neighborhoods:

$$ q_{j/i} = \frac{{\exp ( - \,||\,y_{i} - y_{j} \,||^{2} \,/\,2\upsigma^{2} )}}{{\sum\limits_{k \ne i} {\exp ( - \,||\,y_{i} - y_{k} \,||^{2} \,/\,2\upsigma^{2} )} }} $$

(2)

A natural measurement of the faithfulness with which q_j|i models p_j|i is the Kullback-Leibler divergence (which is in this case equal to the cross-entropy up to an additive constant).SNE minimizes the sum of K-L divergences over all data points using a gradient descent method. The cost function C is given by

$$ c = \sum\limits_{i} {KL(P_{i} \,||\,Q_{i} )} = \sum\limits_{i} {\sum\limits_{j} {p_{j|i} \,\log } } \frac{{p_{j|i} }}{{q_{j|i} }} $$

(3)

The minimization of the cost function in Eq. (3) is performed using a gradient descent method. The gradient has a surprisingly simple form

$$ \frac{{\updelta\,c}}{{\updelta\,y_{i} }} = 2\sum\limits_{j} {(p_{j|i} - q_{j|i} + p_{i|j} - q_{i|j} )(y_{i} - y_{j} )} $$

(4)

Mathematically, the gradient update with a momentum term is given by

$$ y(t) = y(t - 1) +\upeta\frac{{\updelta\,c}}{{\updelta\,y}} +\upalpha(t)(y(t - 1) - y(t - 2)) $$

(5)

Where y(t) indicates the solution at iteration t, η indicates the learning rate, and $\upalpha(t)$ represents the momentum at iteration t.

4.2 t-Distributed Stochastic Neighbor Embedding

Paper [9] points out that SNE for the effect of pulling in pairwise data is stronger than pushing them away. It will squeeze the low dimensional space, which leads to the low dimensional embedding distortion.t-SNE is a variation of SNE. It uses a Student-t distribution rather than a Gaussian to compute the similarity between two points in the low-dimensional space. And t-SNE overcomes the shortcomings of squeezing the low dimensional space. t-SNE is capable of retaining the local structure of the data while also revealing some important global structure.

In t-SNE, define the joint probabilities in the high-dimensional space to be the symmetrized conditional probabilities:

$$ P_{ij} = \frac{{p_{j|i} + p_{i|j} }}{2} $$

(6)

Using Student-t distribution, the joint probabilities are defined as

$$ q_{ij} = \frac{{(1 + \,||\,y_{i} - y_{j} \,||^{2} )^{ - 1} }}{{\sum\limits_{k \ne l} {(1 + \,||\,y_{k} - y_{l} \,||^{2} )^{ - 1} } }} $$

(7)

Therefore, the gradient of the K-L divergence between P and the Student-t based joint probability distribution Q

$$ \frac{{\updelta\,c}}{{\updelta\,y_{i} }} = 4\sum\limits_{j} {(p_{ij} - q_{ij} )(y_{i} - y_{j} )(1 + \,||\,y_{i} - y_{j} \,||^{2} )}^{ - 1} $$

(8)

5 t-SNE Based on Inner Distance

5.1 Key Point Extraction

For 3D shapes, the surfaces may have tens of thousands of points, and the calculation of the inner distance based on voxel between all points is too large. In order to improve the speed of calculation, we preferred [10] iterative method based on the remote priority to extract a certain number of key points from surfaces to represent the entire body. The key points can preserve a good shape feature. On this paper, we extract 300 key points, and will get a 300 × 300 inner distance matrix (Fig. 3).

Fig. 3.

The display of whole points and 300 key points

5.2 t-SNE Based on Inner Distance

For t-SNE, the pairwise similarities in the high-dimensional space are modeled as stochastic neighbor selection probability, but its essence is still the Euclidean distance. Therefore, for the nonlinear data, such as 3D objects, the global Euclidean distance will deviate from the true distance on the manifold, which leads to stochastic neighbor selection probability is not accurate.

We know that inner distance can describe the isometric geometric structure of nonrigid shapes. Therefore, apply t-SNE to the 3D shapes isometric deformation in which Euclidean distances are replaced by inner distance in high-dimensional space.

$$ P_{j/i} = \frac{{\exp ( - d_{ij}^{2} \,/\,2\upsigma^{2} )}}{{\sum\limits_{k \ne i} {\exp ( - d_{ik}^{2} \,/\,2\upsigma^{2} )} }} $$

(9)

Where $d_{ij}$ is the inner distance between key point i and key point j.

And t-SNE based on Inner Distance algorithm (In-tSNE) can be summarized by the following steps,

• 1. compute joint probabilities in the high-dimensional space $p_{ij} = \frac{{p_{j|i} + p_{i|j} }}{2}$ Where is calculated by using Eq. 9

• 2. set sample initial solution $y(t - 1) = \{ y_{1} ,y_{2} , \ldots ,y_{n} \}$, the number of iterations T, learning rate η

• 3. compute the joint probabilities Q (using Eq. 7)

• 4. compute the gradient of the K-L divergence(using Eq. 8)

  $$ \frac{{\updelta\,c}}{{\updelta\,y_{i} }} = 4\sum\limits_{j} {(p_{ij} - q_{ij} )(y_{i} - y_{j} )(1 + \,||\,y_{i} - y_{j} \,||^{2} )}^{ - 1} $$

• 5. calculation of $y(t) = y(t - 1) +\upeta\frac{{\updelta\,c}}{{\updelta\,y}} +\upalpha(t)(y(t - 1) - y(t - 2))$

• 6. go to step3 until the number of iterations t reaching T

6 Experimental Results

In order to describe the correctness of In-tSNE algorithm proposed in 3D isometric deformation, we compared it with tSNE using Euclidean-Distance to show the advantage of inner distance. As is show in Fig. 4, Euclidean-Distance cannot have a good visual effect, especially for the fifth-row shape, because Euclidean-Distance lacks of blending stability. K-L divergence is used to measure the error of distance matrix between high-dimensional and embedding space, as listed at the third column and fifth column.

Fig. 4.

Display of 3D isometric deformation using tSNE with inner distance or Euclidean distance in high-dimensional space.

Also, we compared In-tSNE with the LS-MDS algorithm proposed by Elad and Kimmel. As is seen in Fig. 5, In-tSNE algorithm has a better visual effect on 3D shapes isometric deformation than LS-MDS. We can see, the effect of local convergence using LS-MDS is not ideal, and LS-MDS appears discrete points on the sides of 3D shapes. We used K-L divergence to measure the error between Inner distance matrix in high-dimensional space and Euclidean distance matrix in embedding space. As is shown in Fig. 5, the third column is the KL divergence of In-tSNE, and the fifth column is the KL divergence of LS-MDS. So, In-tSNE is obviously smaller than the KL divergence of LS-MDS. We have done isometric deformation testing on TOSCA [11] and PSBDATA [12] graphic library,and achieved a good display effect.

Fig. 5.

Display of 3D isometric deformation between In-tSNE and LS-MDS

7 Conclusion

In this article, we propose a method for 3D shapes isometric deformation using t-SNE based on inner distance (In-tSNE). We use inner distance to replace the Euclidean distances in high-dimensional space, because inner distance has the certain bending stability. And In–tSNE algorithm has achieved a better effect compared with LS-MDS in shapes isometric deformation.

In the future research, we will try to further research and improve this manifold embedding algorithm and wish to apply this method to other fields such as shape matching, 3D face recognition.