S-box: L-L Cascade Chaotic Map and Line Map

Abstract

Being as an important nonlinear component of block ciphers, Substitution box (S-box) directly affect the security of the cryptographic systems. It is important and difficult to design cryptographically strong S-box that simultaneously meet with multiple cryptographic criteria such as bijection, non-linearity, strict avalanche criterion (SAC), bits independence criterion (BIC), differential probability (DP) and linear probability (LP). To address the issue, an S-box generation approach based on L-L cascade Chaotic Map and Line Map (LLCMLM) is proposed in this paper. L-L cascade chaotic map is used to generate an integer sequence ranging 0–255, and line map is applied to scramble the position of the integer sequence. A series of experiments have been conducted to compare multiple cryptographic criteria of LLCMLM with other algorithms. Simulation results indicate that LLCMLM meets well with the design criteria of the S-box.

1 Introduction

With dynamic developments in the multimedia industry and internet, a large amount of worry has been brought up regarding the security of digital images transmitted over open or stored channels [1–3]. How to protect digital images from being unauthorized handled is becoming extremely crucial. As a branch of modern cryptography, digital images encryption is one of the most useful techniques for images security [4]. Block cipher algorithm is an important research direction in modern cryptography, which has the features of high speed, ease of standardization and software and hardware implementation, therefore it is an effective mean of digital images encryption. In block cipher algorithm, Substitution box (S-box) is the only one nonlinear component of cryptographic algorithm [5], providing the block cipher system with necessary confusing and scrambling effect against attacks. And its cryptography security features directly determine the safety of the entire cipher performance [1]. Mathematically, a n × n size of S-box is a non-linear mapping S : {0, 1}ⁿ → {0, 1}ⁿ, here {0, 1}ⁿ represents the vector spaces of n elements from GF(2), we set n = 8 in this paper.

S-box has the following main design criteria [6–8]: Nonlinearity, strict avalanche criterion (SAC), bits independence criterion (BIC), differential probability (DP) and linear probability (LP). The construction methods of S-box can be divided into two categories: one is based on the structure of mathematical functions including logarithmic functions, exponential functions, inverse map of finite fields and power function of finite fields. The other is a random selection method of construction, i.e., selecting better performance S-box from some randomly generated S-boxes [9]. There exist, however, two main disadvantages in these approaches, poor performance S-box and large amounts of computing resources consumption.

In recent years, most secure systems generate the S-box by chaotic scheme as it has some advantages such as ergodicity, pseudo-randomness and unpredictability. Literature [9] proposed a four-steps method of generating chaotic S-box based on discrete Logistic map. Literature [10] improved the work in [9] by means of bit extraction and Baker map. Furthermore, literature [11] proposed an S-box design approach based on iteration discrete chaotic. Literature [12] developed an S-box generating method using three-dimensional chaotic Baker map.

These algorithms have a common characteristic that they have strong S-boxes using the chaotic maps’ random distribution property. However, the performance gap between the some of these chaotic S-boxes and classic ones still exists, for example, few chaos based S-boxes can achieve the high performance like the one used in advanced encryption standard (AES) [13].

To tackle this issue, researchers have attempted to design the S-boxes in the way of incorporating the advantages of the chaotic S-boxes and the genetic algorithms [13]. For example, literature [14] developed a new way of constructing S-box, that is combing chaotic maps and simulated annealing, thus resulting good performance. However, such schemes choose only one criterion, for example, the nonlinearity, for optimization in the process of designing the S-boxes [13].

Later, some literatures applied the chaotic system to the construction of S-boxes. Literature [15] used the continuous-time Lorenz system to design S-box. Literature [16] proposed to generate S-box by means of Rössler and Lorenz chaotic system. Moreover, Literature [17] presented an S-box design method based on Duffing chaotic system. For more S-box design approaches base on chaotic system, readers can refer to literatures [18–20].

Although we can obtain some S-boxes of good cryptography performance using the chaotic model, the non-linearity and differential uniformity of these S-boxes are still not ideal. And the generation of some superior performance S-boxes still has some difficulties. For example, output sequence constructed by the single chaotic system can not reach the theoretical random completely, due to the limited precision of computer, thus resulting the cyclical issues of the pseudo-random sequence [21].

Researchers have shown that multi-chaotic system and more complex chaotic systems can be applied to enhance security and produce pseudo-random sequences of excellent statistical properties. In this paper, we propose an S-box generation approach based on L-L cascade Chaotic Map and Line Map (LLCMLM). L-L cascade chaotic map is used to construct an integer sequence ranging 0–255, and line map is applied to scramble the position of the integer sequence. The experimental results show that LLCMLM meets well with the design criteria of S-box.

2 Cascade Chaotic Map and Line Map

2.1 Cascade Chaotic Map

We represent the cascade of two Logistic maps as L-L cascade [22]. Logistic map is,

$$ x_{n + 1} = \mu x_{n} (1 - x_{n} ) $$

(1)

where $\mu$ is the system parameter, $\mu \in [0,4]$, x is the initial value, $x \in [0,1]$. Because of its simple structure and complex behavior, it has been widely studied and applied. However, the chaotic map range of the Logistic system is small, that is, it is full map at the unit interval [0, 1] and can present strong chaotic characteristics only when $\mu = 4$. Figure 1(a), (b) depict the bifurcation diagram of the Logistic system and Lyapunov exponent. A smaller range chaotic map may have closer iteration values and may be easier to appear shorter cycle and kinetics degradation when performing quantization in a digital system.

Fig. 1.

The bifurcation diagrams of Logistic map and L-L cascade map and Lyapunov exponents (a) the bifurcation diagram of Logistic map, (b) the Lyapunov exponents of Logistic map, (c) the bifurcation diagram of L-L cascade map (d) the Lyapunov exponents of L-L cascade map ($\mu_{1} = 4$)

In order to improve the dynamics of Logistic map, we process to cascade and observe its dynamics performance improvement. Logistic map cascade of two parameters $\mu_{1}$ and $\mu_{2}$ can be expressed as,

$$ x_{n + 1} = \mu_{1} [\mu_{2} x_{n} (1 - x_{n} )]\{ 1 - [\mu_{2} x_{n} (1 - x_{n} )]\} $$

(2)

where, $\mu_{1}$, $\mu_{2} \in [0,4]$, x is the initial value [0, 1]. To extend the range of the full map and enhance chaotic characteristics, we set $\mu_{1} = 4$, $\mu_{2}$ be the bifurcation parameter. Figure 1(c), (d) show the bifurcation diagram of L-L cascade system and Lyapunov exponents.

The parameter range of L-L cascade system chaotic map expands larger than that of the Logistic chaotic map. And larger chaotic map parameter range provided a larger key space (with initial values and system parameters as the key), thus can enhancing the difficulty of deciphering and improving security. Comparing with non-full map, full map corresponds to the strength of strong chaos whose iteration value range is large. The latter iteration values may difficultly approximate to the previous iteration values, so we can extend the period of the chaotic sequence of numbers to improve the kinetics degradation of the chaotic sequence. Lyapunov exponents of the L-L cascade system is greater than that of the Logistic system in the chaotic region. The increase of Lyapunov exponent may enhance its initial sensitivity, thus improving its power.

2.2 Line-Map

The main idea of Line-Map [23] is that we insert the line of pixels in the diagonal direction of the image pixel matrix into an adjacent row of pixels to be finally stretched into one-dimensional series, and then folded into the same size of the original image matrix. This can give the original adjacent pixels, not in the original position, high efficiency of scrambling. According to the direction of diagonal, we divide it into left and right line maps. The map transform patterns are shown in Fig. 2.

Fig. 2.

The process of line maps

The Left Line Map.

We assume that $A(i,j),i,j = 0,1, \ldots ,N - 1$ is any point in the image. $L(i),i, j = 0,1, \ldots ,N^{2} - 1$ is the dimensional vector after stretching $A(i, j)$.

$$ L(\sum\limits_{k = 0}^{i - 1} {(4k - 1) + j + 1} ) = A(floor(\frac{4i - j + 1}{2}), floor(\frac{j + 1}{2})) $$

(3)

where $j = 1,2, \ldots ,4i - 1$, $i = 1,2, \ldots ,floor(N/2)$.

$$ \begin{aligned} & L(\sum\limits_{k = 1}^{floor(N/2)} {(4k - 1) + \sum\limits_{k = floor(N/2)}^{i - 1} {(4N + 1-4k) - 4floor(\frac{N + 1}{2}) - 1 + j} } ) \\ & = A(floor(\frac{2N + 2 - j}{2}),2i - N + floor(\frac{j}{2})) \\ \end{aligned} $$

(4)

where $j = 1,2, \ldots ,4N + 1-4i$, $i = floor(N/2) + 1,floor(N/2) + 2, \ldots ,N$

The Right Line Map.

We assume that $A(i,j),i,j = 0,1, \ldots ,N - 1$ is any point in the image. $L(i),i,j = 0,1, \ldots ,N^{2} - 1$ is the dimensional vector after stretching $A(i,j)$.

$$ L(\sum\limits_{k = 0}^{i - 1} {(4k - 1) + j + 1} ) = A(floor(\frac{4i - j + 1}{2}), M + 1 - floor(\frac{j + 1}{2})) $$

(5)

where $j = 1,2, \ldots ,4i - 1$, $i = 1,2, \ldots ,floor(N/2)$.

$$ \begin{aligned} & L(\sum\limits_{k = 1}^{floor(N/2)} {(4k - 1) + 2N(i - 1)} + j) \\ & = A(floor(\frac{2N + 2 - j}{2}), M - 2i + 2 + \bmod (N,2) - floor(\frac{j + 2}{2})) \\ \end{aligned} $$

(6)

where $j = 1,2, \ldots ,2N$, $i = 1,2, \ldots ,floor((M - 2floor(N/2))/2)$.

$$ \begin{aligned} & L(\sum\limits_{k = 1}^{floor(N/2)} {(4k - 1) + 2N \cdot floor((M - 2floor(N/2))/2)} ) \\ & + \sum\limits_{k = 0}^{i - 1} {(2(M - M_{1} ) + 5 - 4k) - 2(M - M_{1} ) - 5 + j)} \\ & = A(N - floor(\frac{j - 1}{2}),M - M_{1} - 2i + 3 + floor(\frac{j}{2})) \\ \end{aligned} $$

(7)

where $j = 1,2, \ldots ,2(M - M_{1} ) + 5 - 4i$; $i = 1,2, \ldots ,1 + floor((M - M_{1} )/2)$.

After stretching the image to a $N^{2}$ line $L(i)$, we also fold it into a picture,

$$ B(i,j) = L(i \times N + j) $$

(8)

where $i = 0,1, \ldots ,N - 1$, $j = 0,1, \ldots ,N - 1$.

3 Algorithm Description

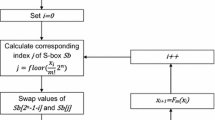
In summary, we can conclude the proposed algorithm as follows.

• Step 1. The initial value $x_{0}$ is substituted into Eq. (1), iterate $N_{0}$ times to obtain $x_{1}$, and define a length of 256 integer array.

• Step 2. With $x_{1}$ as the initial value, we begin to value from $N_{0} + 1$, the real value of the resulting sequences is denoted by $x_{i} ,i = 1,2, \ldots$.

• Step 3. Substitute $x_{i}$ into Eq. (9) to obtain an integer $Q_{i}$ in range [0, 255].

  $$ Q_{i} = \bmod (floor(x_{i} \times 10^{3} ,256)) $$

  (9)

• Step 4. If $Q_{i}$ has appeared in the array $S$, abandon $Q_{i}$, otherwise, deposit $Q_{i}$ into $S$. When the array is filled in, the S-box is generated.

• Step 5. The sequence of integers $S$ is arranged in a 16 × 16 table to construct an initial prototype S-box.

• Step 6. Use left line map to perform S-box m times and right line map n times, and fold the addressed S-box.

4 S-box Evaluation Criteria

In order to obtain the S-box of desired cryptography properties, many scholars designed many criteria to test S-box, among which Bijectivity, nonlinearity, Strict avalanche criterion, Bit independent criterion, Differential approximation probability, Linear approximation probability are widely accepted and adopted. In this paper, the evaluation of S-boxes will also use these criteria.

4.1 Bijectivity

Adamas C and Tavares S defined that f is bijective for a $n \times n$ S-box, if the sum of linear operation of Boolean functions of each component is $2^{n - 1}$ [7],

$$ {\text{wt}}(\sum\limits_{i = 1}^{n} {a_{i} f_{i} } ) = 2^{n - 1} $$

(10)

where $a_{i} \in \{ 0,1\}$, $(a_{1} ,a_{2} , \ldots ,a_{n} ) \ne (0,0, \ldots ,0)$, wt() represents Hamming Weight.

The reversibility of S-box is usually required, especially in a displacement of the network S-box.

4.2 Nonlinearity

Definition 1.

Let $f(x):F_{2}^{n} \to F_{2}$ is an n Boolean function, the non-linearity of f(x) can take the form,

$$ N_{f} = \mathop {\hbox{min} }\limits_{{l \in L_{n} }} d_{H} (f,l) $$

(11)

where, L_n is a set of all linear and affine functions, $d_{H} (f,l)$ represents the Hamming distance between f and l.

The non-linearity represented by Walsh spectrum can take a different form,

$$ N_{f} = 2^{ - n} (1 - \mathop {\hbox{max} }\limits_{{\omega \in GF(2^{n} )}} \left| {S_{ < f > } (\omega )} \right|) $$

(12)

The cyclic spectrum of f(x) is,

$$ S_{ < f > } (\omega ) = 2^{ - n} \sum\limits_{{x \in GF(2^{n} )}} {( - 1)^{f(x) \oplus x \cdot \omega } } $$

(13)

where, $\omega \in GF(2^{n} ),x \cdot \omega$ represents the dot product of x and w.

The larger the nonlinearity N_f of the function f, the stronger the ability of its resisting to the linear attacks, and vice versa.

4.3 Strict Avalanche Criterion

Webster A F and Tavares S E proposed strict avalanche criterion. Strict avalanche criterion describes this fact that when one bit in the input of Boolean function changes, the changing probability of every bit in its output should be 1/2. In practical application, a correlation matrix, the construction method of which can be found in literature [6], is always constructed to test SAC property of the Boolean function.

4.4 Bit Independent Criterion

Adams C and Tavares S proposed Bit independent criterion [7]. For the given Boolean function $f_{j} ,f_{k} (j \ne k)$ is a two bits output of an S-box, if $f_{j} \oplus f_{k}$ is highly nonlinear and meets the SAC, it is possible to ensure that the correlation coefficient of each output bit pair is close to 0 when one input bit is inversed. Therefore, we can check the BIC of the S-box by verifying whether $f_{j} \oplus f_{k} (j \ne k)$ of any two output bits of the S-box meets the nonlinearity and SAC.

4.5 Differential Approximation Probability

The Differential probability DP_f is used to reflect the XOR distribution of the input and output of the Boolean function [9], i.e., maximum likelihood of outputting Δy, when the input is Δx,

$$ DP_{f} = \mathop {\hbox{max} }\limits_{{\Delta x \ne 0,\Delta y}} (\frac{{ \ne \{ x \in X|f(x) \oplus f(x \oplus\Delta x\} =\Delta y}}{{2^{n} }}) $$

(14)

where, X represents the set of all possible inputs, 2ⁿ is the number of elements in the set.

The smaller the DP_f, the stronger the ability of the S-box for fighting against differential cryptanalysis attacks, vice versa.

4.6 Linear Approximation Probability

Under the condition of randomly selecting two masks $\varGamma x$ and $\varGamma y$, we use $\varGamma x$ to calculate the mask of all possible values of input x, and use $\varGamma y$ to calculate the mask of the output values S(x) of the corresponding S-box. Mask the input and the output, and the maximum number of the same results is called the maximum linear approximation [24], which can be computed by the following equation,

$$ LP = \mathop {\hbox{max} }\limits_{\varGamma x,\varGamma x \ne 0} \left| {\frac{{ \ne \{ x|x \cdot \varGamma x = S(x) \cdot \varGamma y\} }}{{2^{n} }} - \frac{1}{2}} \right| $$

(15)

where, $\varGamma x$ and $\varGamma y$ are the mask values of the input and output, respectively, X is a set of all possible input values of x, the elements of which is 2ⁿ.

The smaller the LP, the stronger the ability of the S-box for fighting against linear cryptanalysis attacks, and vice versa.

5 S-box Performance Analysis

To validate the LLCMLM, we compare it with the algorithms in literatures [9–12, 14–20], respectively. And our experimental environment is Inter Core i3 CPU 540 3.07 GHz, memory 2.00 GHz. The program runs in Matlab2012b version. Set initial values of L-L cascaded chaotic map, $x_{0} = 0.1$, $N_{0} = 500$, parameters $\mu_{1} = 4$, $\mu_{2} = 2$, m = 7, n = 1, thus resulting a 8 × 8 S-box, as shown in Table 1. Next, we test the S-box according to the above design criteria.

Table 1. The S-box generated by LLCMLM

5.1 Bijectivity of the S-box of LLCMLM

According to the formula (13), we compute the bijectivity of the generated S-box. The computed value of S-box is just the desired value 128. This indicates that S-box of the LLCMLM meets the bijectivity.

5.2 Nonlinearity of the S-box of LLCMLM

Using (16) to calculate the non-linearity of the S-box of LLCMLM, the results are shown in Table 2. The minimum degree of a non-linear design of S-box 8 Boolean functions is 104 and a maximum of 108, with an average of 106.25. Comparing with the algorithms in literatures [9–12, 14–20], LLCMLM has a larger nonlinearity, shown in the nonlinearity column of Table 6. The results showed that the S-boxes are non-linear, and have the ability to resist linear cryptanalysis.

Table 2. The dependence matrix of the S-box of LLCMLM

5.3 Strict Avalanche Criterion of the S-box of LLCMLM

The testing results are shown in Table 2, the maximum strict avalanche criterion of the generated S-box is 0.5625, the minimum is 0.3906, the average is close to the ideal value of 0.5. Comparing with the results of the literatures [9–12, 14–20], shown in the SAC column of Table 6, the S-box of LLCMLM can better meet the strict avalanche criterion.

5.4 Bit Independent Criterion of the S-box of LLCMLM

The results of the testing are shown in Tables 3 and 4. The average value of non-linearity of the S-box of LLCMLM is 103.64, The average value of correlation matrix is 0.5007, which is close to the ideal value of 0.5. Comparing with the results of literatures [9–12, 14–20], shown in BIC column of Table 6, S-box has a better bit independent criterion.

Table 3. BIC-nonlinearity criterion for the S-box of LLCMLM

Table 4. BIC-SAC criterion for the S-box of LLCMLM

5.5 Differential Approximation Probability of the S-box of LLCMLM

We use Eq. (17) to calculate differential approximation probability of the generated S-box, shown in Table 5. And comparing with the results of literatures [9–12, 14–20], shown in the DP column of Table 6, the results show that the maximum value of differential approximation probability of the S-box of LLCMLM is only 10, the minimum is 4, which means that the generated S-box has a good ability to resist differential cryptanalysis.

Table 5. Differential approximation probability of the S-box of LLCMLM

Table 6. Cryptanalysis comparison results of S-boxes

5.6 Linear Approximation Probability of the S-box of LLCMLM

In this subsection, we use (18) to calculate Linear approximation probability of the generated S-box and compare LLCMLM with other algorithms proposed in literatures [9–12, 14–20]. The experimental results are shown in the right column of Table 6. For LLCMLM, it obtains a greater LP, 0.140625. And the remaining columns are the nonlinearity, SAC, BIC-SAC and BIC results of the comparison algorithms. Table 6 indicates that all of the chaotic based comparison algorithms can generate S-boxes with good performance, however, LLCMLM may obtain an S-box that has a better performance of resisting modern cryptanalysis attacks such as differential and linear cryptanalysis attacks.

6 Conclusion

An S-box generation approach based on L-L cascade Chaotic Map and Line Map (LLCMLM) is designed in this paper. LLCMLM uses L-L cascade chaotic map to generate an integer sequence ranging 0–255, and applies line map to scramble the position of the integer sequence. A series of experiments have been conducted to compare multiple cryptographic criteria of LLCMLM with other algorithms. The experimental results show that the S-box of the CSABC has some good cryptography features such as Bijectivity, Non-linearity, strict avalanche criterion (SAC), bit independent criterion (BIC), differential probability (DP) and linear probability (LP), and it can effectively resist to some attacks. Though LLCMLM can be used to find the S-box with good Cryptography performance, it is still hard to find some S-boxes with very good Cryptography performance. In the future, we will further clarify the relationship between chaos and cryptography, and research how to set chaos parameters to find the S-box with excellent performance.