A Guess-Then-Algebraic Attack on LFSR-Based Stream Ciphers with Nonlinear Filter

Abstract

This paper introduces a new parameter called 1-st minimum algebraic immunity $AI_{min}(f)$, along with some theoretical properties of $AI_{min}(f)$. Based on our results, we propose a guess-then-algebraic attack on LFSR-based stream ciphers with nonlinear filter Boolean function f. Our method takes some particular guessing strategy by taking advantage of the properties of $AI_{min}(f)$, and makes full use of each guessed bit to generate as many equations of degree $AI_{min}(f)$ as possible. The cost of time and data is less than that of the traditional algebraic attack under some condition. Our attack suggests that $AI_{min}(f)$ should not be too small, which is a new design criterion for the filter Boolean function f. We apply our method to a 80-stage keystream generator with a MAI Boolean function f as its filter, while $AI_{min}(f)$ is very small, which disobeys our criterion. The time and data complexities of the traditional algebraic attack are $O(2^{73.56})$ and $O(2^{24.52})$ respectively, with a memory cost of $O(2^{49})$. The time and data complexity of our method are $O(2^{56.86})$ and $O(2^{5.36})$ respectively, and the memory cost is $O(2^{10.72})$.

1 Introduction

The research of the LFSR-based stream ciphers with nonlinear filter generators or combination generators has spawned many analytical methods and theoretical research. A most important cryptanalytic tool is algebraic attack.

Courtois, N.T. and Meier, W. proposed algebraic attack on stream ciphers with linear feedback in 2003 [3], which is a classical and efficient analytical method towards LFSR-based stream ciphers. The basic idea of the algebraic attack is divided into three steps:

Step 1: Construct a nonlinear equation system $\mathcal {A}$ with the secret key bits or initial vector values as its variables by using the keystream bits.

Step 2: Multiply a nonzero function g of low degree to each equation of the system, resulted to an equation system $\mathcal {B}$ with degree lower than that of $\mathcal {A}$.

Step 3: Solve the equation system $\mathcal {B}$.

Since algebraic attack was proposed, there have emerged many research issues related to it. Scholars try to explore the properties of the nonzero function g in Step 2, resulting to the research areas of algebraic immunity and annihilators for the Boolean functions [1, 2, 4, 6, 8, 10, 12, 13, 15, 16]. Denote $AN(f)=\{g \in B_{n}|f\cdot g=0\}$. Any function $g \in AN(f)$ is called an annihilator of f. The algebraic immunity of f, named AI(f), is the minimum algebraic degree of nonzero annihilators of f or $f+1$ [11], which measures the ability of the Boolean functions against algebraic attack. The maximum algebraic immunity for n-variable Boolean functions is $\lceil \frac{n}{2}\rceil$ [3], and a Boolean function with maximum algebraic immunity is called MAI Boolean function.

In this paper, for a Boolean function $f\in B_{n}\,$(where $B_{n}$ is the n-variable Boolean ring), we introduce a parameter called 1-st minimum algebraic immunity $AI_{min}(f)$. We prove that when AI(f) is optimum, $AI_{min}(f)\le AI(f)$, particularly, when n is odd, $AI_{min}(f)< AI(f)$. A simple algorithm is given to compute $AI_{min}(f)$.

When the filter of a LFSR-based stream cipher is a MAI Boolean function f, it can resist the algebraic attack to the greatest extent. Based on our theoretical results related to $AI_{min}(f)$, we propose a guess-then-algebraic attack on such kind of LFSR-based stream ciphers. The strategy of guessing is very important in the guess and determine attack. Our method takes some particular guessing strategy by taking advantage of the properties of $AI_{min}(f)$. First, we guess some initial state bits, the locations of which are determined by the specific structure of the LFSR and the properties of $AI_{min}(f)$. After guessing enough LFSR state bits, we derive equations of degree $AI_{min}(f)$ as many as possible by taking advantage of the specific structure of the LFSR and the filter taps, and then we solve the resulted equation system.

Our method has three special merits. (a) It makes full use of each guessed bit to derive equations of degree $AI_{min}(f)$ as many as possible. In fact, $AI_{min}(f)$ is strictly less than AI(f) in most cases. (b) It utilizes not only the properties of f but also the tap positions, which helps to derive as much information as possible. The cost of time and data is less than that of the traditional algebraic attack given in [3] under some condition. (c) Our attack suggests that $AI_{min}(f)$ should not be too small, which is a new design criterion for the filter Boolean function f.

Moreover, we apply our method on a 80-stage keystream generator. Its filter generator is a 9-variable MAI Boolean function f, while $AI_{min}(f)$ is very small, which disobeys our design criterion. This model can resist the traditional algebraic attack given in [3] to the greatest extent. The time and data complexities of the traditional algebraic attack are $O(2^{73.56})$ and $O(2^{24.52})$ respectively, with a memory cost of $O(2^{49})$. While the time and data complexity of our method are $O(2^{56.86})$ and $O(2^{5.36})$ respectively, and the memory cost is $O(2^{10.72})$.

Notice that Debraize, B. and Goubin, L. proposed a guess-and-determine algebraic attack on the self-shrinking generator (SSG) with low Hamming weight feedback polynomial in [7]. It mainly aims to analyze the self-shrinking generators, while our method targets to the LFSR-based stream ciphers with filter Boolean functions of optimum algebraic immunity. They guess some information first, then write a system of polynomial equations and solve the system with SAT solver algorithm MiniSAT. While our method pays attention to the locations of the guessed bits by taking advantage of the theoretical properties of $AI_{min}(f)$, which is a new parameter in the academic sector of the stream cipher. Moreover, the degree of the equations derived after guessing some state bits is $AI_{min}(f)$, which is the most different character between our method and the guess-and-determine algebraic attack proposed in [7].

This paper is organized as follows: Sect. 2 introduces some basic knowledge related to our work. In Sect. 3, we introduce a new parameter called 1-st minimum algebraic immunity $AI_{min}(f)$, along with some theoretical analysis. We also give a simple algorithm to compute $AI_{min}(f)$. In Sect. 4, for LFSR-based keystream generators with nonlinear filter Boolean function, we propose a guess-then-algebraic attack by taking advantage of $AI_{min}(f)$ and give some design criterion of the LFSR-based keystream generators. In Sect. 5, we apply our method to a keystream generator which does not obey our criterion. Section 6 concludes this paper.

2 Preliminaries

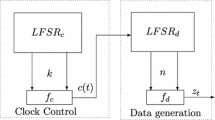
Courtois, N.T. and Meier, W. proposed the algebraic attack on stream ciphers with linear feedback [3]. They mainly focused on the LFSR-based keystream generators with nonlinear filter Boolean function. Figure 1 shows the general model.

Fig. 1.

LFSR-based keystream generator with nonlinear filter

First, we give a brief description for this model. Let the length of the linear feedback shift register be l. L is the “connection function” of the LFSR, and it is linear. Let the initial state of the LFSR be $s^{0}=(s_{0},s_{1},...,s_{l-1})$, then it generates a m-sequence $s_{0},s_{1},s_{2}...$. For sake of narrative convenience, we call this m-sequence as LFSR sequence. The state of the LFSR at time t is

$$s^{t}=(s_{t},s_{t+1},...,s_{t+l-1})=L^{t}(s_{0},s_{1},...,s_{l-1}),$$

which is filtered by a balanced nonlinear Boolean function $f\in B_{n}$. The generator outputs one bit $c_{t}$ at time t. For each $c_{t}$, we can construct an equation involving some key bits and initial value as its variables. Denote the output of the filter generator by $c_{0},c_{1},c_{2},...$, where $c_{i} \in F_{2}$, then we can get the following equation system:

$$\begin{aligned} \left\{ \begin{array}{lll} c_{0}=f(s_{0},s_{1},...,s_{l-1})\\ c_{1}=f(L(s_{0},s_{1},...,s_{l-1}))\\ c_{2}=f(L^{2}(s_{0},s_{1},...,s_{l-1}))\\ \vdots \\ \end{array}\right. \end{aligned}$$

(1)

The problem of recovering the l initial state bits of the LFSR is reduced to solving the equation system (1).

Table 1. Complexity of AA for the model in Fig. 1

Table 1 shows the complexity of the traditional algebraic attack (AA) in [3] on the model given in Fig. 1, where $M=\left( {\begin{array}{c}l\\ AI(f)\end{array}}\right)$, and $\omega$ is the parameter of the Gaussian elimination and in theory $\omega \le 2.376$ [5].

While as the authors of [3] declare, the (neglected) constant factor in that algorithm is expected to be very big and they regard Strassen’s algorithm [14] as the fastest practical algorithm. Then they evaluate the complexity of the Gaussian reduction to be $7\cdot M^{log_{2}^{7}}/64$ CPU clocks. For convenience, scholars usually use $\omega =3$ in Table 1 to estimate the time and data complexity of the traditional algebraic attack.

We can get that the complexity of the traditional algebraic attack on the model given in Fig. 1 is determined by l and AI(f). When using the traditional algebraic attack given in [3], for each keystream bit, the lowest degree of equations that the analysts can obtain is AI(f). In the next section, we try to find a way to see if we can decrease the time and data complexity by further exploring the properties of the nonlinear filter function and the structure of the filter tap positions.

3 1-st Minimum Algebraic Immunity $AI_{min}(f)$

In this section, for a Boolean function $f \in B_{n}$, we give a new definition called 1-st minimum algebraic immunity $AI_{min}(f)$. To begin with, we give the following definition.

Definition 1

Given a Boolean function $f(x_{1},x_{2},...,x_{n}) \in B_{n}$, for some fixed i, $i \in [1,n]$, define

$$AI(f|_{x_{i}=0})=AI(f(x_{1},x_{2},...,x_{i-1},0,x_{i+1},...,x_{n})).$$

$$AI(f|_{x_{i}=1})=AI(f(x_{1},x_{2},...,x_{i-1},1,x_{i+1},...,x_{n})).$$

Definition 2

Given a Boolean function $f(x_{1},x_{2},...,x_{n}) \in B_{n}$, for some fixed i, $i \in [1,n]$, define

$$AI_{i}(f)=max\{AI(f|_{x_{i}=0}),AI(f|_{x_{i}=1})\}.$$

Definition 3

For a Boolean function $f(x_{1},x_{2},...,x_{n}) \in B_{n}$, define the 1-st minimum algebraic immunity of f as

$$AI_{min}(f)=min\{AI_{i}(f):i\in [1,n]\}.$$

Also define

$$N_{AI_{min}}(f)=\sharp \{i|AI_{i}(f)=AI_{min}(f):i\in [1,n]\},$$

where “$\sharp$” denote the number of the elements in a set.

Let $G=\{g\in AN(f|_{x_{i}=c})|deg(g)=AI_{min}(f)\}$, and also denote $n_{i,c}=\sharp G$, where $c \in \{0,1\}$.

Based on the above definitions, we derive Theorem 1:

Theorem 1

For a Boolean function $f(x_{1},x_{2},...,x_{n}) \in B_{n}$, if its algebraic immunity is optimum, then

$$AI_{min}(f)\le AI(f).$$

Particularly, if n is odd, then

$$AI_{min}(f)< AI(f).$$

Proof

Given $f(x_{1},x_{2},...,x_{n}) \in B_{n}$, it can be expressed as:

$$f(x_{1},x_{2},...,x_{n})=x_{i}f_{1}(x_{1},...,x_{i-1},x_{i+1},...,x_{n})+f_{2}(x_{1},...,x_{i-1},x_{i+1},...,x_{n}).$$

When $x_{i}$ is fixed, there are only $n-1$ variables left, then from Definitions 1–3, we can get that

$$AI_{min}(f)\le AI_{i}(f)\le \lceil \frac{n-1}{2}\rceil \le AI(f).$$

Particularly, if n is odd, then

$$AI_{min}(f)\le AI_{i}(f)\le \lceil \frac{n-1}{2}\rceil < \lceil \frac{n}{2}\rceil =AI(f).$$

The following example verifies Theorem 1.

Example 1

The Boolean function $f=x_{1}x_{2}x_{3}x_{5} + x_{1}x_{2}x_{5} + x_{1}x_{2} + x_{1}x_{3}x_{4}x_{5} + x_{1}x_{3}x_{4} + x_{1}x_{3}x_{5} + x_{1}x_{4}x_{5} + x_{1}x_{4} + x_{2}x_{3} + x_{2}x_{4}x_{5} + x_{2}x_{5} + x_{3}x_{4} + x_{4}x_{5} + 1$ is a 5-variable Carlet-Feng Boolean function. We can get that $AI(f)=3$, which is optimum. The $AI_{i}(f), i \in [1,5]$ of f are listed in Table 2.

Table 2. Compute the $AI_{i}(f)$ of f

We can see that $AI_{min}(f)=AI_{i}(f)=2<AI(f)=3$, $N_{AI_{min}}(f)=5>1$.

In fact, for a Boolean function $h\in B_{n}$, although AI(h) is not maximum, it is possible that $AI_{min}(h)$ is strictly less than AI(h). For instance, for the filter function $f_{d}$ adopted by the stream cipher LILI-128 [9], $AI_{min}(f_{d})=3< AI(f_{d})=4$, $N_{AI_{min}}(f_{d})=4$.

Algorithm 1 shows how to compute $AI_{min}(f)$ and $N_{AI_{min}}(f)$ for a Boolean function f.

4 A Guess-Then-Algebraic Attack on LFSR-Based Stream Ciphers via Our Theoretical Results

Designers often choose a MAI Boolean function as the filter of the LFSR-based keystream generators, which helps to resist the traditional algebraic attack to the greatest extent. Section 3 shows that for a Boolean function f of optimum algebraic immunity, $AI_{min}(f)\le AI(f)$. Even if AI(f) is not maximum, it is possible that $AI_{min}(f)< AI(f)$. We consider to take advantage of the properties of $AI_{min}(f)$ to recover the initial state of the LFSR.

The strategy of guessing is very important in the guess and determine attack. In this section, we would like to give a guess-then-algebraic attack, which takes some particular guessing strategy by taking advantage of the properties of $AI_{min}(f)$ proposed in Sect. 4. First we choose to guess some (initial) internal state bits of the LFSR, resulted to equations of degree $AI_{min}(f)$. Here we make use of each guessed bit to the greatest extent, that is, we would use each guessed bit to construct as many low-degree equations as possible. The positions of the guessed internal state bits of the LFSR should obey some rules according to the detailed structure of the LFSR, the properties of the filter Boolean function, and the filter tap positions. After guessing a suitable number of (initial) internal state bits, we can get an equation system of degree $AI_{min}(f)$.

In the following, we propose an attack by using our theoretical results in Sect. 3. We focus on the LFSR-based keystream generator with nonlinear filter shown in Fig. 1. With the same description in Sect. 2, we target to recover the initial state bits $s^{0}=(s_{0},s_{1},...,s_{l-1})$ by solving the following equation system:

$$\begin{aligned} \left\{ \begin{array}{lll} c_{0}=f(s_{0}^{1},s_{0}^{2},...,s_{0}^{n})\\ c_{1}=f(s_{1}^{1},s_{1}^{2},...,s_{1}^{n})\\ c_{2}=f(s_{2}^{1},s_{2}^{2},...,s_{2}^{n})\\ \vdots \\ \end{array}\right. \end{aligned}$$

(2)

where $s_{t}^{i}, i=1,2,...,n$ are the n LFSR state bits tapped as the input of the filter Boolean function $f(x_{1},x_{2},...,x_{n})$ at time t.

Guess-then-algebraic Attack:

Assume that the LFSR shifts right and it is regularly clocked.

Step I: For $f(x_{1},x_{2},...,x_{n})\in B_{n}$, compute $AI_{min}(f)$, E and $N_{AI_{min}}(f)$ via Algorithm 1. Suppose we get $E\!=\!\{(x_{i_{1}},AI_{min}(f),n_{i_{1},0},n_{i_{1},1}),...,(x_{i_{m}}, AI_{min}(f),n_{i_{m},0}, n_{i_{m},1}):1 \le i_{1}<i_{2}< \cdots <i_{m}\le n\}$, $N_{AI_{min}}(f)=m$, $AI_{min}(f)=k$.

Step II: With the parameters derived from Step I, we do the following operation:

(1) At time t, denote the inputs of the filter function as $s_{t}^{1},...,s_{t}^{n}$, find the LFSR state bit corresponding to $x_{i_{1}}$ in set E, and denote it as $s_{t}^{i_{1}}$.

(2) Guess $s_{t}^{i_{1}}=a$, where $a\in \{0,1\}$, then we can derive an equation

$$f_{t}(s_{t}^{1},s_{t}^{2},...,s_{t}^{i_{1}-1},a, s_{t}^{i_{1}+1},..., s_{t}^{n})=c_{t}.$$

From Algorithm 1 we get that $AI(f_{t})=AI_{min}(f)=k$.

(3) For each clock, denote the distance of the locations for the LFSR state bits corresponding to the variables $x_{i}$ and $x_{j}$ of f as $d_{i,j}$.

Notice that $E\!=\!\{(x_{i_{1}},AI_{min}(f),n_{i_{1},0},n_{i_{1},1}),...,(x_{i_{m}},AI_{min}(f),n_{i_{m},0}, n_{i_{m},1}):1 \le i_{1}<i_{2}< \cdots <i_{m}\le n\}$, then we clock the stream cipher $d_{i_{1},i_{2}}$ clocks from time t. Find the LFSR state bit corresponding to $x_{i_{2}}$ in the set E at time $t+d_{i_{1},i_{2}}$, and denote it as $s_{t+d_{i_{1},i_{2}}}^{i_{2}}$. With the keystream bit $c_{t+d_{i_{1},i_{2}}}$ and the guessed value of $s_{t}^{i_{1}}=a$, we get another equation at time $t+d_{i_{1},i_{2}}$ by substitute $s_{t+d_{i_{1},i_{2}}}^{i_{2}}$ by a.

$$f_{t+d_{i_{1},i_{2}}}(s_{t+d_{i_{1},i_{2}}}^{1},s_{t+d_{i_{1},i_{2}}}^{2},...,s_{t+d_{i_{1},i_{2}}}^{i_{2}-1},a,s_{t+d_{i_{1},i_{2}}}^{i_{2}+1},..., s_{t}^{n})=c_{t+d_{i_{1},i_{2}}}\!.$$

In the same way, we can get a group of m equations, and the algebraic immunity of the functions $f_{t},f_{t+d_{i_{1},i_{2}}},...,f_{t+d_{i_{1},i_{m}}}$ is $AI_{min}(f)=k$.

$$\begin{aligned} \left\{ \begin{array}{lll} f_{t}(s_{t}^{1},...,s_{t}^{i_{1}-1},a, s_{t}^{i_{1}+1},..., s_{t}^{n})=c_{t}\\ f_{t+d_{i_{1},i_{2}}}(s_{t+d_{i_{1},i_{2}}}^{1},...,s_{t+d_{i_{1},i_{2}}}^{i_{2}-1},a,s_{t+d_{i_{1},i_{2}}}^{i_{2}+1},..., s_{t+d_{i_{1},i_{2}}}^{n})=c_{t+d_{i_{1},i_{2}}}\\ \vdots \\ f_{t+d_{i_{1},i_{m}}}(s_{t+d_{i_{1},i_{m}}}^{1},...,s_{t+d_{i_{1},i_{m}}}^{i_{m}-1},a,s_{t+d_{i_{1},i_{m}}}^{i_{m}+1},..., s_{t+d_{i_{1},i_{m}}}^{n})=c_{t+d_{i_{1},i_{m}}}\\ \end{array}\right. \end{aligned}$$

(3)

Until now, we get m equations by guessing one LFSR state bit. For each equation, we can derive $n_{i_{j},c_{t+d_{i_{j},i_{k}}}}$ (or $n_{i_{j},c_{t+d_{i_{j},i_{k}}}+1}$ when $c_{t+d_{i_{j},i_{k}}}=0$) equations of degree $AI_{min}(f)$, where $n_{i_{j},c_{t+d_{i_{j},i_{k}}}}$ is the number of annihilators defined in Definition 3. We guess another LFSR state bit which is appropriately chosen, and get another group of equations, and so on.

We hope that the guessed bits are all the initial state bits of the LFSR, which can make the analysis much easier. If the guessed bits are not all the initial state bits, more careful analysis is needed.

Usually, we choose the parameter $t=0$, for it can make the number of the guessed initial bits among all the guessed LFSR state bits as large as possible, which can make the analysis much easier.

Here we analyze the situation that the guessed bits are all the initial state bits of the LFSR. Suppose we guess r initial LFSR state bits, then we can get $r\cdot \sum _{1\le j< k\le m}n_{i_{j},c_{t+d_{i_{j},i_{k}}}}$ equations with the initial LFSR state bits as the variables by using the linear feedback recursion of the LFSR. Then we use the same method to analyze the complexity with the method mentioned in [3].

After guessing r LFSR initial state bits, we reduce the problem of solving the l initial LFSR state bits with a filter Boolean function f of algebraic immunity AI(f) to solving $l-r$ unknown initial bits with a filter Boolean function of algebraic immunity $AI_{min}(f)$.

When the condition

$$\begin{aligned} r\cdot \sum _{1\le j< k\le m}n_{i_{j},c_{t+d_{i_{j},i_{k}}}} \ge \left( {\begin{array}{c}l-r\\ AI_{min}(f)\end{array}}\right) \end{aligned}$$

(4)

is satisfied, the time complexity to solve the equation system derived from Step II is

$$T_{1}=N^\omega ,$$

where $N=\left( {\begin{array}{c}l-r\\ AI_{min}(f)\end{array}}\right)$, and $\omega$ is the parameter of the Gaussian elimination, and we adopt $\omega =3$ in this paper. The complexity to recover the initial state of the LFSR is

$$T=2^{r}N^\omega .$$

The data that we need is

$$D=max(rm,\left( {\begin{array}{c}l-r\\ AI_{min}(f)\end{array}}\right) ).$$

The key condition is that the inequality (4) is satisfied. In fact, when $AI_{min}(f)$ is small enough (especially when $AI_{min}(f)=1$), the condition can be satisfied in most cases. Under this situation, we can directly see that the data complexity is better than that of the algebraic attack in [3]. While the improvement of the time complexity is not determined. It can be derived that the time complexity of our attack is less than that of the conventional algebraic attack given in [3] when r satisfies the following inequality:

$$\begin{aligned} \frac{r}{w}< log_{2}{l\atopwithdelims ()d}-log_{2}{l-r\atopwithdelims ()k}, \end{aligned}$$

(5)

where r is the number of the guessed initial state bits, $d=AI(f)$, $k=AI_{min}(f)$, and $\omega$ is the parameter of the Gaussian elimination.

In fact, the number of the equations that can be derived by guessing r-bit initial state can be more than $r\cdot \sum _{1\le j< k\le m}n_{i_{j},c_{t+d_{i_{j},i_{k}}}}$ if we can make full use of the annihilators for $f|_{x_{i}=c}$. Let $G=\{g\in AN(f|_{x_{i}=c})|deg(g)=AI_{min}(f)\}$, for an element $g\in G$, multiply monomials of degree less than $AI_{min}(f)$ to g, and we may get new polynomials that can be used to construct equations.

Our method suggests a new design criterion for the filter Boolean function f adopted by the LFSR-based stream ciphers, that is, the parameters of the keystream generator should not satisfy the inequality (4) and inequality (5) in the same time, which means that designers should pay attention that their keystream generator should satisfy that:

• (a)$AI_{min}(f)$ should be large enough to resist our guess-then-algebraic attack.

• (b)The number of variables corresponding to $AI_{min}(f)$ should not be too large.

Notice that our method can be applied to all kinds of LFSR-based stream ciphers with nonlinear filter. If the target stream cipher satisfies the inequalities (4) and (5), then we can decrease the time and data complexity.

5 Application of Our Method on a LFSR-Based Stream Cipher Overlooking Our Criterion

In this section, we would like to give an example to show that the $AI_{min}(f)$ should not be too small for the nonlinear filter Boolean function.

The target model is the same with the one shown in Fig. 1. The length of the LFSR is 80, and its initial state bits are $(s_{0}, s_{1},...,s_{79})$. The linear feedback polynomial is primitive. The filter Boolean function is a 9-variable Boolean function $f=f(x_{1}, x_{2},...,x_{9})$, AI(f) is optimum. Suppose the LFSR shifts left and it is regularly clocked. The 9 inputs to f are taken from LFSR according to this full positive difference set: (0,1,3,7,12,20,30,44,65).

From the above description we can get that this model can resist the traditional algebraic attack given in [3] to the greatest extent. In the following, we would show that although AI(f) is optimum, our method works if the model disobeys our criterion mentioned in Sect. 4.

Suppose $AI_{min}(f)=1$, and the corresponding variable is $x_{7}$, that is, $AI(f|_{x_{7}=0})=AI(f|_{x_{7}=1})=1$, which means that this model disobeys our criterion.

According to the guess-then-algebraic attack given in Sect. 4, we can guess $r=41$ initial state bits $(s_{38}, s_{31},...,s_{79})$. Then we can get at least 41 linear equations, which satisfy the inequality (4), that is $r \ge \left( {\begin{array}{c}80-r\\ AI_{min}(f)\end{array}}\right) =39$. The time complexity of our attack is

$$T=2^{r}\left( {\begin{array}{c}80-r\\ 1\end{array}}\right) ^\omega =2^{56.86},$$

where m is the number of variables for f corresponding to $AI_{min}(f)$.

The data complexity is

$$D=max(r,\left( {\begin{array}{c}80-r\\ 1\end{array}}\right) =2^{5.36}.$$

The memory complexity is

$$M=2^{10.72}.$$

Table 3 shows the comparison between our method (GA) and the traditional attack (AA) given in [3] on this model.

Table 3. Comparison between GA and AA in [3]

Remark 1

This example verifies that although the target model obsesses a filter Boolean function of optimum algebraic immunity, if it disobeys our criterion, analysts can still use our guess-then-algebraic attack to recover the initial state with time and data complexities less than that of the traditional algebraic attack given in [3].

6 Conclusion

This paper introduces a new parameter called 1-st minimum algebraic immunity $AI_{min}(f)$ for the Boolean function f, along with some theoretical properties of $AI_{min}(f)$. Based on our results, we propose a guess-then-algebraic attack on the LFSR-based stream cipher with nonlinear filter Boolean function f by guessing some state bits in advance and then applying algebraic attack on it. Our method makes full use of each guessed bit to generate as many equations of degree less than or equal to AI(f) as possible. The cost of time and data is less than that of the traditional algebraic attack in [3] under some condition. Our method suggests a new design criterion for the LFSR-based keystream generators with nonlinear filter. We apply our method to a 80-stage keystream generator with a MAI Boolean function f as its filter, while $AI_{min}(f)$ is very small, which disobeys our criterion. The time, memory and data complexities of our method are less than that of the traditional algebraic attack.