Semantic Scene Classification with Generalized Gaussian Mixture Models

Abstract

The work proposed in this paper is motivated by the need to develop powerful approaches for scene classification which is a challenging problem mainly due to varying conditions. In this paper, we are mostly interested in automatically assigning a scene image to a semantic category when RGB channels and near infrared information are simultaneously available. We represent images by a collection of local image patches that we use to learn a global generalized Gaussian mixture (GGM) using the split and merge expectation-maximization (SMEM) algorithm. Using this approach, we built an effective scene classification system capable of handling outliers and noise level in the data. Extensive experiments show the merits of the proposed framework.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Recently, scene understanding and classification has gained a lot of interest. The goal of scene classification is to automatically classify a scene image to a semantic category based on analyzing the visual content of the image. Most of existing computer vision approaches are applied on visible (RGB) images due to their wide availability. However, lighting condition represents one of the most challenging problem when dealing with RGB images. Hence, researchers were encouraged to employ thermal infrared sensors. Despite its robustness to illumination changes, infrared has various drawbacks such as its sensitivity to ambient temperature and its higher cost compared to RGB cameras. Thus, some researchers decided to look beyond the conventional visible band and into the near-infrared (NIR) part of the electromagnetic spectrum (700–1100 nm). NIR has three main advantages: 1- robust to variation in ambient lighting compared to visible images, 2- less affected by ambient temperature relative to infrared, 3- can work in both daytime and nighttime. Furthermore, NIR images can be easily obtained by removing the NIR blocking filter affixed to digital cameras. Moreover, RGB and NIR cues have been successfully combined in many applications [1, 2]. In this paper, we examine whether fusion of visual and NIR images can increase the overall performance of scene classification systems.

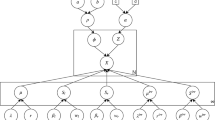
Most existing scene classification approaches differ by: the image representation method, the learning algorithm, and the classification method. In [3], the authors built a scene classification system without the need for segmenting and processing individual objects or regions. The work in [4] presented an approach to find intermediate semantic models of natural scenes using region-based information. Firstly, the scene images are divided into local regions, which are represented by a combination of a color and a texture feature. Secondly, through so-called concept classifiers (k-NN or SVM), the local regions are classified. Thirdly, each image is represented by a concept occurrence vector (COV) computed as the histogram of the semantic concepts. Finally, in order to classify a novel image, its COV representation is used as input to an additional SVM. However, a large number of local regions of training images need to be annotated manually with the above semantic concepts which is not effective. In [5], the authors presented an approach based on local invariant features and probabilistic latent semantic analysis (pLSA). Motivated by this work we try to model the semantic of the image in an unsupervised manner. In the training process, we represent an image by a collection of local image patches from which we extract local features that we quantize into a visual codebook using a global mixture model. Next, we use the posterior to distribute each patch in the image to the best component in the mixture (codeword) in order to represent each image with a histogram of codeword occurrences. Then, we use these bag-of-words (BoW) histograms as feature vectors to discover “Z” latent topics using pLSA. Finally, we use the topics representation of the training images to learn an SVM classifier. In the testing phase, each input image is partitioned into patches and local features are extracted from each patch. Next, it is represented by a BOW histogram and then its topic distribution vector is determined. Finally, SVM is used to choose the best category to the image. A complete diagram of our approach is shown in Fig. 1. Generally, the Gaussian is used, but is not the best choice in real life applications. Therefore, we consider the generalized Gaussian density (GGD) has been widely used recently for its flexibility. Moreover, we use the split and merge EM (SMEM) for the parameters estimation.

Fig. 1.

Complete diagram of our approach

The rest of this paper is organized as follows. Section 2 introduces the GGM and its parameters estimation algorithm. In Sect. 3, we present the method used for scene classification. We assess the performance of the new approach on RGB and NIR images; while comparing it to other model in Sect. 4. Our last section is devoted to the conclusion.

2 The GGM and Its Parameters Estimation Algorithm

In this paper, we break all training images down into orderless N patches. Then we select a 40 dimensional feature vector for each patch (D=40). Thus, the input for our GGM is a set of N i.i.d vectors $\mathcal {X}$= (${\varvec{X}}_{1}$,..., ${\varvec{X}}_{N}$), each of D-dimensions ${\varvec{X}}_{{\varvec{i}}} = [X_{i1},\ldots ,X_{iD}]^T$. If we assume that $\mathcal {X}$ arise from a finite generalized Gaussian mixture model with K components then:

$$\begin{aligned} p(\mathcal {X}|\varTheta ) = \prod _{i=1}^{N}\sum _{j=1}^{K} p({\varvec{X}}_{i}|\xi _j) p_j \end{aligned}$$

(1)

where $p({\varvec{X}}_{i}|\xi _j)$ is a generalized Gaussian probability distribution given by:

$$\begin{aligned} \small p({\varvec{X}}_{i}|\xi _j) = \prod _{d=1}^{D} \frac{\lambda _{jd} \bigg [\frac{\varGamma (3/\lambda _{jd})}{\varGamma (1/\lambda _{jd})}\bigg ]^{1/2}}{2\sigma _{jd}\varGamma (1/\lambda _{jd})} \exp \bigg [-A(\lambda _{jd})\bigg |\frac{X_{id}-\mu _{jd}}{\sigma _{jd}}\bigg |^{\lambda _{jd}}\bigg ] \end{aligned}$$

(2)

where $A(\lambda _{jd})$ $=$ $\bigg [\frac{\varGamma (3/\lambda _{jd})}{\varGamma (1/\lambda _{jd})}\bigg ]^{\lambda _{jd}/2}$; $\xi _j$ is the set of the parameters of the j component given by $\xi _j$=($\varvec{\mu }_{j}$, $\varvec{\sigma }_{j}$, $\varvec{\lambda }_{j}$) where $\varvec{\mu }_{j}$ = ($\mu _{j1}$,...,$\mu _{jD}$), $\varvec{\sigma }_{j}$ = ($\sigma _{j1}$,...,$\sigma _{jD}$), $\varvec{\lambda }_{j}$ = ($\lambda _{j1}$,..., $\lambda _{jD}$) are the mean, the standard deviation, and the shape parameters of the D-dimensional GGD, respectively. Note that $p_j$ are the mixing proportions which must be positive and sum to one and $\varTheta$ the set of parameters of the mixture with K classes is defined by $\varTheta$ = ($\varvec{\mu }_{1}$,..., $\varvec{\mu }_{K}$, $\varvec{\sigma }_{1}$,..., $\varvec{\sigma }_{K}$, $\varvec{\lambda }_{1}$,..., $\varvec{\lambda }_{K}$, $p_1$,...,$p_K$). The EM algorithm for the GGM can be summarized as [6]

• 1. Start with an initialized parameter set $\varTheta ^{(0)}$

• 2. Compute the posterior probabilities: $p(j|{\varvec{X}}_{i}) = \frac{p({\varvec{X}}_{i}|\xi _j^{(l)})p_j^{(l)}}{\sum _{j=1}^{K}p({\varvec{X}}_{i}|\xi _j^{(l)})p_j^{(l)}}$

• 3. Compute a new set of parameters:

  $$\begin{aligned} \hat{p}_j^{(l+1)} = \frac{1}{N} \sum _{i=1}^{N} p(j|{\varvec{X}}_{i}) \end{aligned}$$

  (3)
  $$\begin{aligned} \small \hat{\mu }_{jd}^{(l+1)} = \frac{\sum _{i=1}^{N} p(j|{\varvec{X}}_{i})|X_{id}-\mu _{jd}|^{\lambda _{jd}-2}X_{id}}{\sum _{i=1}^{N} p(j|{\varvec{X}}_{i})|X_{id}-\mu _{jd}|^{\lambda _{jd}-2}} \end{aligned}$$

  (4)
  $$\begin{aligned} \small \hat{\sigma }_{jd}^{(l+1)} = \bigg [\frac{\lambda _{jd}A(\lambda _{jd})\sum _{i=1}^{N} p(j|{\varvec{X}}_{i})|X_{id}-\mu _{jd}|^{\lambda _{jd}}}{\sum _{i=1}^{N} p(j|{\varvec{X}}_{i})}\bigg ]^{1/\lambda _{jd}} \end{aligned}$$

  (5)
  $$\begin{aligned} \small \hat{\lambda }_{jd}^{(l+1)} \simeq \lambda _{jd} - \bigg [\bigg (\frac{\partial ^2 \log [p(\mathcal {X}|\varTheta )]}{\partial \lambda _{jd}^{2}}\bigg )^{-1} \bigg (\frac{\partial \log [p(\mathcal {X}|\varTheta )]}{\partial \lambda _{jd}}\bigg )\bigg ] \end{aligned}$$

  (6)

• 4. If the parameter estimates converge, then stop. Otherwise, go to Step 2.

The SMEM algorithm is based on the following: 1- use the EM algorithm represented above until convergence; 2- use a split and merge criteria to choose two components (g, h) to merge and one component q to split; 3- apply an efficient method to initialize the merged and split parameters; 4- perform the next EM round; 5- iterate split-and-merge and the EM until meeting some criterion.

2.1 Split and Merge Parameters Initialization

The combination of the gth and hth components are merged into the $g*$th component by matching the zeroth, first, second, and fourth moments:

$$\begin{aligned} \small p_{g*}=p_{g}+p_{h} \end{aligned}$$

(7)

$$\begin{aligned} \small p_{g*}\mu _{g*d}=p_{g}\mu _{gd}+p_{h}\mu _{hd} \end{aligned}$$

(8)

$$\begin{aligned} \small p_{g*}(\mu ^{2}_{g*d}+\sigma ^{2}_{g*d})=p_{g}(\mu ^{2}_{gd}+\sigma ^{2}_{gd})+p_{h}(\mu ^{2}_{hd}+\sigma ^{2}_{hd}) \end{aligned}$$

(9)

$$\begin{aligned} p_{g*}\bigg (\sigma ^{4}_{g*d}\frac{\varGamma (5/\lambda _{g*d}) \varGamma (1/\lambda _{g*d})}{\varGamma ^2(3/\lambda _{g*d})}+6\mu ^{2}_{g*d}\sigma ^{2}_{g*d} +\mu ^{4}_{g*d}\bigg )= \nonumber \\ p_{g}\bigg (\sigma ^{4}_{gd}\frac{\varGamma (5/\lambda _{gd}) \varGamma (1/\lambda _{gd})}{\varGamma ^2(3/\lambda _{gd})}+6\mu ^{2}_{gd}\sigma ^{2}_{gd} +\mu ^{4}_{gd}\bigg )+\nonumber \\ p_{h}\bigg (\sigma ^{4}_{hd}\frac{\varGamma (5/\lambda _{hd}) \varGamma (1/\lambda _{hd})}{\varGamma ^2(3/\lambda _{hd})}+6\mu ^{2}_{hd}\sigma ^{2}_{hd} +\mu ^{4}_{hd}\bigg ) \end{aligned}$$

(10)

Suppose that we want to split the qth component in the mixture to two components g and h. Thus, we construct a set of solutions for this problem:

$$\begin{aligned} \small p_{g}=u_1 p_{q} \qquad p_{h}=(1-u_1) p_{q} \end{aligned}$$

(11)

$$\begin{aligned} \small \mu _{gd}=\mu _{qd}-u_2\sigma _{qd} \sqrt{\frac{p_{h}}{p_{g}}} \quad \mu _{hd}=\mu _{qd}+u_2\sigma _{qd} \sqrt{\frac{p_{g}}{p_{h}}} \end{aligned}$$

(12)

$$\begin{aligned} \small \sigma ^2_{gd}= u_3 (1-u_2^2)\sigma ^2_{qd} \frac{p_{q}}{p_{g}} \quad \sigma ^2_{hd}= (1-u_3) (1-u_2^2)\sigma ^2_{qd} \frac{p_{q}}{p_{h}} \end{aligned}$$

(13)

where $u_1$, $u_2$, and $u_3$ are randomly sampled from the Beta distribution $\beta (2,2)$, $\beta (2,2)$, $\beta (1,1)$, respectively. For $\varvec{\lambda }_{g}$ and $\varvec{\lambda }_{h}$ we set them equal to $\varvec{\lambda }_{q}$.

2.2 Split and Merge Criteria

We define the following merge criterion:

$$\begin{aligned} \small J_{merge}(g,h,\varTheta )= \frac{P_g(\varTheta )^T P_h(\varTheta )}{||P_g(\varTheta )||||P_h(\varTheta )||} \end{aligned}$$

(14)

where $P_j(\varTheta )=(p(j|{\varvec{X}}_{1}),\ldots ,p(j|{\varvec{X}}_{N}))$, T denotes the transpose operation, and ||.|| denotes the Euclidean vector norm. If the two components g and h have large $J_{merge}(g,h,\varTheta )$ then they are a good candidate for the merge. For the split criterion, we adopt the local Kullback divergence as:

$$\begin{aligned} \small J_{split}(q,\varTheta )=\int f_q(\mathcal {X}|\varTheta ) \log \frac{f_q(\mathcal {X}|\varTheta )}{p(\mathcal {X}|\xi _q)} dx \end{aligned}$$

(15)

where $f_q(\mathcal {X},\varTheta )$ is an empirical distribution weighted by the posterior probability [7]. Thus, if the component q has the largest $J_{split}(q,\varTheta )$ this means that it has the worst estimate and we should try to split it. Therefore, the SMEM algorithm can be summarized by:

• 1. Run EM algorithm from initial parameters $\varTheta ^{(0)}$ until convergence $\varTheta ^{*}$

• 2. Sort the Split and Merge candidates using $\varTheta ^{*}$ (described in 2.2). Let $(g,h,q)_c$ denotes the cth candidate.

• 3. For $c=1, ..., C_{max}$ initialize the split and merge parameters (See 2.1).

• 4. Perform the full EM algorithm until convergence $\varTheta ^{**}$

• 5. If $\log [p(\mathcal {X}|\varTheta ^{**})]$ $>$ $\log [p(\mathcal {X}|\varTheta ^{*})]$ then set $\varTheta ^{*}$ $\leftarrow$ $\varTheta ^{**}$, $\log [p(\mathcal {X}|\varTheta ^{*})]$ $\leftarrow$ $\log [p(\mathcal {X}|\varTheta ^{**})]$, and go to step 2

Fig. 2.

Sample images from the EPFL scene classification data set.

3 Experimental Results: Scene Classification

In our approach, an image is represented as a number of 5$\times$5 patches. Our next step is feature extraction. For RGB images, experimental evaluation of several color models has indicated significant correlations between the colour bands and that the luminance component amounts to around 90 % of the signal energy, thus, we consider only the luminance channel. On the other hand, NIR has only one channel that has a much weaker dependence on R, G and B than they do to each other. Moreover, we consider the Haralick texture measurements [8] derived from the Gray-Tone Spatial Dependency Matrix (GLCM). Following [9], we calculate four angular Gray-Tone Spatial Dependency Matrices with 1 or 2 pixel offsets for each patch. Therefore we end up with 8 GLCMs for any image patch. Using these matrices, we extract 5 features namely: dissimilarity, Angular Second Moment (ASM), mean, standard deviation (STD) and correction. Thus, we end up with 40 component feature vector measures for each image patch. The next step is to use the global GGM introduced above to build a codebook for the data set, where each component in the mixture represents a codeword. Knowing, the different codewords we can deduce the BoW histogram for each image by classifying each patch to the component that gives the highest posterior probability. Later, we apply the pLSA model to the bag of visual words representation which allows the description of each image as a Z-dimensional vector, where Z is the number of aspects (or learnt topics) [10]. Finally, SVM classifier is used via LIBSVM package [11].

Fig. 3.

Confusion tables for scene classification.

Table 1. Classification accuracy.

Our experimental study is applied on the EPFL scene classification data set (EPFL) [12]. This dataset consists of 477 images in 9 categories, (Country (52), Field (51), Forest (53), Mountain (55), Indoor (56), Old Building (51), Street (50), Urban (58),Water (51)), captured in RGB and NIR. As described in [12], the NIR images in this data set were captured by removing the NIR blocking filter in the digital camera. Sample images of different categories from the EPFL data set are displayed in Fig. 2. The major challenge in this data set is the overlap between object categories. For example urban and old building classes can be confused with each others also country can be confused with water class. For evaluation, we followed the same protocol as in [2] where we randomly selected, 10 times, 11 images per class for testing and trained the classifier using the remaining images. Firstly, we experiment with various different sizes of the visual vocabulary or in our case GGM components (80–512). We found that starting from K = 125 the classification accuracy did not changed as compared to difference in computational time. Thus, we have chosen to use K=125 in our approach. Concerning the number of latent topics used in the pLSA model we have used Z = 25. In order to assess if NIR can be a good alternative for RGB in classification, we applied our approach on the RGB images as well as the NIR images. In the case of using both RGB and NIR information together, we have built two codebooks: one for the luminance channel and one for NIR channel. Then, in order to fuse both information, we concatenated both BOW histograms together as input to the pLSA model. Figure 3 shows the confusion matrix of the EPFL data set for RGB, NIR, and RGB+NIR, respectively. In order to validate our method, we have compared it with the same method when K-means and Euclidean distance are used for codebook construction and BOW histogram calculation. From Table 1 we can conclude that our approach outperformed the K-means method. In addition, NIR performs better than RGB in case of scene classification, and fusing both the RGB and NIR cues together shows a small improvement over both individual results which confirms that both cues contain complementary information.

4 Conclusion

This paper makes three contributions. First, we implement a SMEM approach for the estimation of the GGM parameters. This approach can overcome the EM problem related to local maxima. Second, we use a global GGM to build a codebook for the image data set. This approach overcome the different problems of using K-means due to its robustness to outliers and noise level. Finally, we explore the idea that near-infrared (NIR) information, captured from an ordinary digital camera, can be useful in scene recognition. The obtained results show the merits of the approach.