Abstract
This paper reorganizes and further develops the theory of partial meet contraction which was introduced in a classic paper by Alchourrón, Gärdenfors and Makinson. Our purpose is threefold. First, we put it in a broader perspective by decomposing it into two layers which can respectively be treated by the general theory of choice and preference and elementary model theory. Second, we reprove the two main representation theorems of AGM and present two more representation results for the finite case that “lie between” the former, thereby partially answering an open question of AGM. Our method of proof is uniform insofar as it uses only one form of “revealed preference”, and it explains where and why the finiteness assumption is needed. Third, as an application, we explore the logic characterizing theory contractions in the finite case which are governed by the structure of simple and prioritized belief bases.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
Intuitively, however, I think that liberal maximization is preferable. Liberal maximization is based on strict relations which do not allow to distinguish between incomparabilities and indifferences. Nonstrict relations do make this distinction, but stringent maximization tends to require connected relations which often can be had only if incomparabilities are turned into indifferences—i.e., if augmentations are used. The interpretation of nonstrict relations as the converse complements of—more intuitive—strict relations explains the crucial role of negative transitivity and negative well-foundedness in the following. Also compare the recommendation in Rott (1992b) to regard the nonstrict epistemic entrenchment relation ≤ E of Gärdenfors and Makinson (1988) as the converse complement of a more intuitive strict relation < E .
- 2.
It is worth pointing out that the characteristic definition of a relation of epistemic entrenchment (see Gärdenfors and Makinson 1988; Rott 1992b) between propositions from an observed contraction behavior, viz.
$$\displaystyle{x \leq _{E}y\ iff\ x\notin A\mathop{-}\limits ^{.}(x \wedge y)\ \mathrm{or}\ y \in A\mathop{-}\limits ^{.}(x \wedge y)}$$can also be interpreted as a base preference (Rott 1992b, p. 61). In that paper it is argued that the instruction “remove x ∧ y” should be regarded as an instruction to remove x or remove y, where the agent holding theory A has free choice which proposition(s) out of {x, y} to remove. [Note added in 2015: This sketch of an idea was turned into a theory in Rott (2003).]
- 3.
This is no problem for Lindström (1991) whose selection functions are always ω-covering. Consequently, Lindström’s constructions can always make use of the base preferences \(\mathcal{P}_{2}(\gamma )\).
- 4.
This marks a difference with Lewis (1981) who identifies propositions with sets of extra-linguistic possible worlds and logical consequence with set-theoretic inclusion. Lacking compactness, Lewis has to ponder the impact of a “Limit Assumption” for premise semantics.
- 5.
Both were discovered independently and concern belief revision rather than belief contraction. The first exception is condition (R8) in Katsuno and Mendelzon (1991). The second is the infinitary condition “Gamma” in Lindström (1991) which is labelled (BC7) in its variant for belief revision operations.
- 6.
Incidentally, it is proved in AGM (1985, Observation 6.5) that the conjunction of (\(\mathop{-}\limits ^{.}7\)) and (\(\mathop{-}\limits ^{.}8\)) is equivalent to the even stronger “ventilation condition”
$$\displaystyle{A\mathop{-}\limits ^{.}(x \wedge y) = A\mathop{-}\limits ^{.}x\ \ \mbox{ or}\ \ A\mathop{-}\limits ^{.}(x \wedge y) = A\mathop{-}\limits ^{.}y\ \ \mbox{ or}\ \ A\mathop{-}\limits ^{.}(x \wedge y) = A\mathop{-}\limits ^{.}x \cap A\mathop{-}\limits ^{.}y.}$$ - 7.
In order to reconcile this with your intuitions, cf. Footnote 1.
- 8.
This simplified rephrasing of the AGM construction makes use of the fact that for all M ∈ U A and contraction functions \(\mathop{-}\limits ^{.}\) satisfying the AGM postulates, \(A\mathop{-}\limits ^{.}x \subseteq M\) implies M ∈ A ⊥ x.
- 9.
Nebel’s (1992) treatment of the fully general infinite case is not quite correct. Slips have crept into his claim that his \(C\! \Downarrow \!\phi\) is nonempty, into his definition (9) of ≪ , and into the proof of Proposition 8. As Nebel (personal communication) has suggested, they can be remedied by imposing a condition of converse well-foundedness on \(\preceq\).
- 10.
Or equivalently, \(\mathit{Cn}((\bigcap \{\mathit{Cn}(N)\!: N \in \gamma (B\perp x)\}) \cup \{ x\! \rightarrow \! a\}) = \mathit{Cn}(A\mathop{-}\limits ^{.}{}'x \cup \{ x\! \rightarrow \! a\})\) where \(A\mathop{-}\limits ^{.}{}'x\) follows the first definition.
- 11.
Nebel’s (1992) later paper deals with revisions where this problem does not arise. In fact, if revisions are construed as being generated by the so-called Levi-identity \(A {\ast} x = \mathit{Cn}((A\mathop{-}\limits ^{.}\neg x) \cup \{ x\})\), then the modification made in our official definition does not have any effect on revisions.
- 12.
This appendix was not included in the original 1993 publication of this paper.
References
Alchourrón, C., Gärdenfors, P., & Makinson, D. (1985). On the logic of theory change: Partial meet contraction functions and their associated revision functions. Journal of Symbolic Logic, 50, 510–530.
Alchourrón, C., & Makinson, D. (1986). Maps between some different kinds of contraction function: The finite case. Studia Logica, 45, 187–198.
Arrow, K. J. (1959). Rational choice functions and orderings. Economica, N.S., 26, 121–127.
Chernoff, H. (1954). Rational selection of decision functions. Econometrica, 22, 422–443.
de Condorcet, N. (1785). Essai sur l’application de l’analyse á la probabilité des décisions rendues á la pluralité des voix. Paris: Imprimerie Royale. Reprint Cambridge: Cambridge University Press (2014).
Fuhrmann, A., & Morreau, M. (Eds.) (1991). The logic of theory change (Lecture notes in computer science, Vol. 465). Berlin: Springer.
Gärdenfors, P. (1988). Knowledge in flux: Modeling the dynamics of epistemic states. Cambridge: Bradford Books/MIT.
Gärdenfors, P. (Ed.) (1992). Belief revision. Cambridge: Cambridge University Press.
Gärdenfors, P., & Makinson, D. (1988). Revisions of knowledge systems using epistemic entrenchment. In M. Vardi (Ed.), Theoretical aspects of reasoning about knowledge (pp. 83–95). Los Altos: Morgan Kaufmann.
Grove, A. (1988). Two modellings for theory change. Journal of Philosophical Logic, 17, 157–170.
Hansson, S. O. (1992). Similarity semantics and minimal changes of belief. Erkenntnis, 37, 401–429.
Herzberger, H. G. (1973). Ordinal preference and rational choice. Econometrica, 41, 187–237.
Katsuno, H., & Mendelzon, A. O. (1991). Propositional knowledge base revision and minimal change. Artificial Intelligence, 52, 263–294.
Kraus, S., Lehmann, D., & Magidor, M. (1990). Nonmonotonic reasoning, preferential models and cumulative logics. Artificial Intelligence, 44, 167–207.
Lehmann, D., & Magidor, M. (1992). What does a conditional knowledge base entail? Artificial Intelligence, 55, 1–60.
Lewis, D. (1973). Counterfactuals. Oxford: Blackwell.
Lewis, D. (1981). Ordering semantics and premise semantics for counterfactuals. Journal of Philosophical Logic, 10, 217–234.
Lindström, S. (1991). A semantic approach to nonmonotonic reasoning: Inference and choice. University of Uppsala, April 1991 (manuscript).
Makinson, D., & Gärdenfors, P. (1991). Relations between the logic of theory change and nonmonotonic logic. In Fuhrmann & Morreau (1991) (pp. 185–205).
Nebel, B. (1989). A knowledge level analysis of belief revision. In R. Brachman, H. Levesque, & R. Reiter (Eds.), Proceedings of the 1st International Conference on Principles of Knowledge Representation and Reasoning (pp. 301–311). San Mateo: Morgan Kaufmann.
Nebel, B. (1992). Syntax-based approaches to belief revision. In Gärdenfors (1992) (pp. 52–88).
Rott, H. (1991). Two methods of constructing contractions and revisions of knowledge systems. Journal of Philosophical Logic, 20, 149–173.
Rott, H. (1992a). On the logic of theory change: More maps between different kinds of contraction function. In Gärdenfors (1992) (pp. 122–141).
Rott, H. (1992b). Preferential belief change using generalized epistemic entrenchment. Journal of Logic, Language and Information, 1, 45–78.
Rott, H. (2003). Basic entrenchment. Studia Logica, 73, 257–280.
Samuelson, P. A. (1950). The problem of integrability in utility theory. Economica, N.S., 17, 355–381.
Sen, A. K. (1982) Choice, welfare and measurement. Oxford: Blackwell.
Suzumura, K. (1983) Rational choice, collective decisions, and social welfare. Cambridge: Cambridge University Press.
Uzawa, H. (1956). Note on preference and axioms of choice. Annals of the Institute of Statistical Mathematics, 8, 35–40.
Acknowledgements
I gratefully acknowledge numerous comments and suggestions by David Makinson which have once again been extremely helpful.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix 1: Relating Theory Change and Nonmonotonic Logic
In a recent paper, Makinson and Gärdenfors (1991) make considerable progress toward linking the areas of theory change and nonmonotonic reasoning. They close with the following problem which we quote in full:
We end with an important open question. In their (1985), Alchourrón, Gärdenfors and Makinson established a representation theorem for theory revision operations ∗ satisfying conditions (∗1)–(∗8), in terms of “transitively relational partial meet revisions”. The proof went via a representation theorem for a contraction function \(\mathop{-}\limits ^{.}\) satisfying certain conditions (\(\mathop{-}\limits ^{.}\) 1) – (\(\mathop{-}\limits ^{.}\) 8). On the other hand, Kraus et al. (1990) have established a representation theorem for supraclassical, cumulative and distributive nonmonotonic inference relations \(\;\vert \!\!\!\sim \,\) defined between individual propositions, in terms of classical stoppered preferential model structures. The former proof is relatively short and abstract; the latter seems more complex. Also, the latter has not been generalized to a representation theorem for supraclassical, cumulative and distributive inference operations C: 2L → 2L […] Does the representation theorem for theory change hold the key for a solution to this problem of extending the Kraus/Lehmann/Magidor representation theorem to the infinite case—despite the failure of consistency preservation for preferential model structures? Or do we have two essentially different representation problems? (Makinson and Gärdenfors 1991, pp. 203–204, notation adapted)
This question does not have a simple answer. Three different points have to be taken into consideration.
First, the approaches of AGM and KLM are not as distinct as Makinson and Gärdenfors seemed to assume. AGM contract and revise by single propositions, and similarly KLM consider the nonmonotonic consequences of simple propositions. Makinson and Gärdenfors’s equation y ∈ A ∗ x iff x \(\;\vert \!\!\!\sim \,\) y(iff y ∈ C(x)) fully reflects this. A truly infinitistic stance towards both theory change and nonmonotonic logic is taken only by Lindström (1991). The question of whether the theory A is logically finite has no bearing on this issue. Here Makinson and Gärdenfors saw a difference which simply does not exist.
Secondly, Makinson and Gärdenfors tacitly passed over the fact that in KLM there is no counterpart to (∗8) or (\(\mathop{-}\limits ^{.}\) 8). But this difference is indeed crucial, as is clear from a later paper of Lehmann and Magidor (1992). As regards the preferential logics dealt with by KLM, no “relatively short and abstract” proof seems to be possible. Thus it appears reasonable to construe Makinson and Gärdenfors’s question as referring to the rational logics treated by Lehmann and Magidor.
But thirdly, Lehmann and Magidor’s rational logics still differ from AGM-style theory revisions in that they are not required to satisfy a condition of consistency preservation which corresponds to postulate (\(\mathop{-}\limits ^{.}\) 4) for contractions. In this respect, Makinson and Gärdenfors show a keen sense of the intricacies of the situation. In unpublished notes, we have applied the techniques developed in this paper to the problem of providing rational logics with canonical models. We have found that it is possible to transfer our proof to the area of nonmonotonic logic, but that consistency preservation with respect to the underlying monotonic logic Cn is, in fact, indispensable for a perfect matching. The reason is that the compactness property presupposed for Cn runs idle if there are any “inaccessible worlds” (and this is just what a violation of consistency preservation amounts to). Since the results of our efforts bear considerable similarity with the venerable presentation in Lewis (1973)—except for the fact that the role of Lewis’s extra-linguistic propositions (sets of “real” possible worlds) is played by the propositions of the object language—we had better refrain from expounding them here in more detail.
Appendix 2: Some Proofs and Examples
Proof of Lemma 1.
-
(a)
Immediate from the definition of relationality. (If x is greatest in S′ then it is so in all subsets of S′ in which it is contained. If x is greatest in every S i then it is so in \(\bigcup S_{i}\).)
-
(b)
Let γ be 12-covering and satisfy (I) and (II). We have to show that for every \(S \in \mathcal{X}\), γ(S) = { x ∈ S: for all y ∈ S, \(\{x,y\} \in \mathcal{X}\) and x ∈ γ({x, y})}.\(LHS \subseteq RHS\): Let x ∈ γ(S) and y ∈ S. As γ is 12-covering, \(\{x,y\} \in \mathcal{X}\) and (I) gives us x ∈ γ({x, y}).
\(RHS \subseteq LHS\): Let x ∈ S and assume that for every y ∈ S, \(\{x,y\} \in \mathcal{X}\) and x ∈ γ({x, y}). Note that \(\bigcup \{\{x,y\}: y \in S\} = S \in \mathcal{X}\) and \(x \in \bigcup \{\{ x,y\}: y \in S\}\). By (II), we get \(x \in \gamma (\bigcup \{\{x,y\}: y \in S\}) =\gamma (S)\), as desired.
-
(c)
Let γ be 12-covering and satisfy (I).
\(\mathcal{P}_{2}(\gamma ) \subseteq \mathcal{P}(\gamma )\): This direction is always valid.
\(\mathcal{P}(\gamma ) \subseteq \mathcal{P}_{2}(\gamma )\): Let x ≤ γ y. Then there is an \(S \in \mathcal{X}\) such that \(y \in \gamma (S) \subseteq S\) and x ∈ S. Because γ is 12-covering, \(\{x,y\} \in \mathcal{X}\). But as \(\{x,y\} \subseteq S\), (I) gives us y ∈ γ({x, y}), so x ≤ γ, 2 y.
-
(d)
Follows from (b) and (c).
-
(e)
Follows from (a), (b), and (d).
-
(f)
Let γ be additive and satisfy (I) and (II). We have to show that for every \(S \in \mathcal{X}\), γ(S) = { x ∈ S: for all y ∈ S there is a \(T \in \mathcal{X}\) such that x ∈ γ(T) and y ∈ T}.
\(LHS \subseteq RHS\): Take T = S.
\(RHS \subseteq LHS\): Let x ∈ S and assume that for all y ∈ S there is a T y such that x ∈ γ(T y) and y ∈ T y. Thus \(x \in \bigcap \gamma (T^{y})\) and \(S \subseteq \bigcup T^{y}\). From the former and the additivity of γ we get \(x \in \gamma (\bigcup T^{y})\), by (II), and now the latter and (I) yield x ∈ γ(S), as desired. q.e.d.
Proof of Lemma 2.
-
(a)
Let γ be 12n-covering and satisfy (I). We show the claim for \(\mathcal{P}_{2}(\gamma )\), which is identical with \(\mathcal{P}(\gamma )\), by Lemma 1(c). Suppose for reductio that \(x_{1} <_{ \gamma }^{2}x_{2} <_{ \gamma }^{2}\ldots <_{ \gamma }^{2}x_{n} <_{ \gamma }^{2}x_{1}\) for some \(x_{1},\ldots x_{n} \in X\). That is, \(\gamma (\{x_{i},x_{i+1}\}) =\{ x_{i+1}\}\) with + denoting addition modulo n. Now consider \(\gamma (\{x_{1},\ldots,x_{n}\})\not =\emptyset\). Let \(x_{k} \in \gamma (\{x_{1},\ldots,x_{n}\})\). But x k ∉ γ({x k , x k + 1}). This is in contradiction with (I). The rest of (a) is trivial.
-
(b)
Let γ be 123-covering and satisfy (I) and (III). We show the claim for \(\mathcal{P}_{2}(\gamma )\), which is identical with \(\mathcal{P}(\gamma )\), by Lemma 1(c). Assume that x ≰ γ, 2 y and y ≰ γ, 2 z. By definition of ≤ γ, 2, this means that y ∉ γ({x, y}) and z ∉ γ({y, z}). Now consider γ({x, y, z}). By (I), y ∉ γ({x, y, z}) and z ∉ γ({x, y, z}), so γ({x, y, z}) = { x} since γ({x, y, z}) must be a non-empty subset of {x, y, z}. By (I), x ∈ γ({x, z}), so \(\gamma (\{x,y,z\}) \subseteq \gamma (\{x,z\})\). Hence, by (III), \(\gamma (\{x,z\}) \subseteq \gamma (\{x,y,z\}) =\{ x\}\), so z ∉ γ({x, z}), i.e. x ≰ γ, 2 z, as desired.
-
(c)
Let γ be finitely additive and satisfy (IV), and let x ≤ γ y and y ≤ γ z. This means that there is an \(S \in \mathcal{X}\) such that y ∈ γ(S) and x ∈ S and a \(T \in \mathcal{X}\) such that z ∈ γ(T) and y ∈ T. Now consider \(S \cup T\). Obviously, \(x \in S \cup T\). In order to show that x ≤ γ z it suffices to show that \(z \in \gamma (S \cup T)\). By finite additivity, \(S \cup T \in \mathcal{X}\). By z ∈ γ(T) and (IV), it suffices to show that \(\gamma (S \cup T) \cap T\not =\emptyset\). Suppose for reductio that \(\gamma (S \cup T) \cap T =\emptyset\). Then, since \(\emptyset \not =\gamma (S \cup T) \subseteq S \cup T\), \(\gamma (S \cup T) \cap S\not =\emptyset\). So by (IV), \(\gamma (S) \subseteq \gamma (S \cup T)\). So \(y \in \gamma (S \cup T)\). But since also y ∈ T, \(\gamma (S \cup T) \cap T\not =\emptyset\) after all, and we have a contradiction.
(Notice that an attempted proof of the transitivity of ≤ γ, 2 would also need, apart from the 123-covering condition, (I) in order to come from z ∈ γ({x, y, z}) to z ∈ γ({x, z}), so we can rest content with (c).) q.e.d.
Proof of Lemma 3.
-
(a)
Assume that \(\mathcal{S}(\leq )\) is no selection function over \(\mathcal{X}\). By the definition of \(\mathcal{S}(\leq )\), this can only happen if some \(S \in \mathcal{X}\) possesses no greatest element under ≤ . Thus for every x i ∈ S there is an x i+1 ∈ S such that x i+1 ≮ x 1. This, however, contradicts smoothness. That \(\mathcal{S}(\leq )\) satisfies (I) and (II) follows from Lemma 1(a).
-
(b)
Let γ be relational with respect to some negatively transitive and negatively well-founded relation ≤ . (Or alternatively, let γ be subtractive and relational with respect to some negatively transitive and \(\mathcal{X}\)-smooth relation ≤ .) Let \(S,S' \in \mathcal{X}\), \(S \subseteq S'\) and \(\gamma (S') \subseteq \gamma (S)\). We want to show that \(\gamma (S) \subseteq \gamma (S')\).Suppose for reductio that this is not the case, i.e., that there is some x which is in γ(S) but not in γ(S′). The latter means that there is some y 1 in S′ such that y 1 ≰ x. As x ∈ γ(S), y 1 ∈ S′ − S. But because \(\gamma (S') \subseteq \gamma (S) \subseteq S\), y 1 ∉ γ(S′). So there is some y 2 ∈ S′ such that y 2 ≰ y 1. By negative transitivity, y 2 ≰ x. So by the same reasoning as before, y 2 ∈ S′ − S and y 2 ∉ γ(S′). So there is some y 3 ∈ S′ such that y 3 ≰ y 2. By negative transitivity again, y 3 ≰ x, and the same reasoning can be continued again and again. What we get is an infinite chain \(y_{1},y_{2},y_{3},\ldots\) in S′ − S such that \(\ldots \not\leq y_{3}\not\leq y_{2}\not\leq y_{1}\). But this contradicts the negative well-foundedness of ≤ (or the subtractivity of γ, which guarantees that \(S' - S \in \mathcal{X}\), and smoothness of ≤ ).
-
(c)
Let γ be relational with respect to some transitive relation ≤ . Let \(S,S' \in \mathcal{X}\), \(S \subseteq S'\) and \(x \in \gamma (S') \cap S\). By relationality, the latter conditions says that y ≤ x for all y ∈ S′. Let z ∈ γ(S). We have to show that z ∈ γ(S′), i.e., by relationality, that y ≤ z for all y ∈ S′. But since x ∈ S and z ∈ γ(S), x ≤ z, so since y ≤ x for all y ∈ S′, the desired conclusion follows from the transitivity of ≤ . q.e.d.
Proof of Lemma 4.
-
(a)
Let γ be subtractive.
(I) implies (I ′): Let \(S,S',S \cup S' \in \mathcal{X}\) and \(x \in \gamma (S \cup S')\). As \(S,S' \subseteq S \cup S'\) and x is either in S or in S′, we get \(x \in \gamma (S) \cup \gamma (S')\), by (I), as desired.(I ′) implies (I): Let \(S,S' \in \mathcal{X}\) and \(S \subseteq S'\). By subtractivity, \(S' - S \in \mathcal{X}\) as well. Using \(S' = S \cup (S' - S)\) and (I′), we get \(\gamma (S') \subseteq \gamma (S) \cup \gamma (S' - S)\). Intersecting both sides with S, then, we get \(\gamma (S') \cap S \subseteq (\gamma (S) \cap S) \cup (\gamma (S' - S) \cap S) =\gamma (S)\), since \(\gamma (S) \subseteq S\)
-
(b)
First we note that for finitely additive γ, (II′) is equivalent to
-
(II fin ) For all {S i : i ∈ I, I finite\(\}\subseteq \mathcal{X}\) such that \(\bigcup \{S_{i}: i \in I\} \in \mathcal{X}\), \(\bigcap \{\gamma (S_{i})\!: i \in I\} \subseteq \gamma (\bigcup \{S_{i}\!: i \in I\})\)
Now we simply modify the proof of Lemma 1(f) by taking only finitely many of the T y’s into consideration. This is possible because compactness can be applied to the inclusion \(S \subseteq \bigcup T^{y}\) in that proof.
-
-
(c)
Let γ satisfy (I).
(III) implies (III ′): Let \(S,S \cup S' \in \mathcal{X}\) and \(\gamma (S \cup S') \cap S' =\emptyset\). From the latter condition and \(\gamma (S \cup S') \subseteq S \cup S'\) it follows that \(\gamma (S \cup S') \subseteq S\). Hence, by (I), \(\gamma (S \cup S') = S \cap \gamma (S \cup S') \subseteq \gamma (S)\). Thus, by (III), \(\gamma (S) \subseteq \gamma (S \cup S')\), as desired.(III ′) implies (III): Let \(S,S' \in \mathcal{X}\), \(S \subseteq S'\) and \(\gamma (S') \subseteq \gamma (S)\). Since \(S' = S \cup (S' - S) \in \mathcal{X}\) and \(\gamma (S') \subseteq \gamma (S) \subseteq S\), it holds that \(\gamma (S \cup (S' - S)) \cap (S' - S) =\emptyset\). By (III′), we get \(\gamma (S) \subseteq \gamma (S')\), as desired.
-
(d)
Immediate.
-
(e)
That (I&II) implies (I) is immediate if we put I = { i} and S i = S′, and that (I&II) implies (II) is immediate if we put \(S =\bigcup S_{i}\) and observe that \(\gamma (S_{i}) \subseteq S\). In order to see that (I) and (II) taken together imply (I&II), we note that \(\bigcup \{S_{i}\!: i \in I\} \in \mathcal{X}\), by additivity. So (II) gives us \(S \cap \bigcap \gamma (S_{i}) \subseteq S \cap \gamma (\bigcup S_{i})\), and (I) gives us \(S \cap \gamma (\bigcup S_{i}) \subseteq \gamma (S)\), whenever \(S \subseteq \bigcup S_{i}\). So in this case \(S \cap \bigcap \gamma (S_{i}) \subseteq \gamma (S)\), as desired.
-
(f)
Similar to (e). q.e.d.
Re section “Representation Theorems for Contraction Functions”: Example of a relational partial meet contraction function which does not satisfy ( \(\mathop{-}\limits ^{.}8r\) ).
Consider a propositional language L with denumerably many atoms \(p_{1},p_{2},p_{3},\ldots\) and q and r. Let \(A = Cn(p_{1},p_{2},p_{3},\ldots,q,r)\). Let \(W_{i},W_{i}^{q},W_{i}^{r}\), for \(i = 1,2,3,4,\ldots\), be the maximally consistent set of propositions defined by
\(p_{i} \in W_{i},W_{i}^{q},W_{i}^{r}\), for every i,
\(\neg p_{j} \in W_{i},W_{i}^{q},W_{i}^{r}\), for every i and every j ≠ i,
\(q \in W_{i}^{q}\) n and \(\neg q \in W_{i},W_{i}^{r}\), for every i,
\(r \in W_{i}^{r}\) and \(\neg r \in W_{i},W_{i}^{q}\), for every i.
Let W \(^{qr} =\bigcup \{\{ W_{i},W_{i}^{q},W_{i}^{r}\}: i = 1,2,3,\ldots \}\). Remember that V A = W − [[A]]. Let the relation < W over V A be defined as follows:
W < W W′ for every W ∈ W qr and W′ ∈ V A − W qr
\(W_{j}^{q} <_{W}W_{j+1}\), \(W_{j}^{q} <_{W}W_{j+1}^{q}\), and \(W_{j}^{q} <_{W}W_{j+1}^{r}\), for every \(j \in \{ 0,2,4,6,\ldots \}\)
\(W_{k}^{r} <_{W}W_{k+1}\), \(W_{k}^{r} <_{W}W_{k+1}^{q}\), and \(W_{k}^{r} <_{W}W_{k+1}^{r}\), for every \(k \in \{ 1,3,5,\ldots\)}
These are all pairs standing in the relation < W (see Fig. 16.3).
Then define, for the purposes of this example, M ≤ M′ iff M′ ≮ M iff \(\mathcal{W}(M)\not<_{W}\mathcal{W}(M')\). Then clearly, the ≤ -greatest elements of A ⊥ x correspond to the < -minimal elements of \([\![\neg x]\!]\). Note that ≤ is connected, acyclic and conversely well-founded (no infinite ascending chains), but not negatively transitive. Let \(\mathop{-}\limits ^{.} = \mathcal{C}(\mathcal{S}(\leq ))\) be the relational partial meet contraction determined by ≤ .
Now observe that the greatest elements of \(A\perp (q \wedge r) = A\perp q \cup A\perp r\) are exactly \(A \cap W_{0}\), \(A \cap W_{0}^{q}\), and \(A \cap W_{0}^{r}\). Since p 0 is an element of all these sets, we have \(p_{0} \in A\mathop{-}\limits ^{.}(q \wedge r)\).
The greatest elements of A ⊥ q are \(A \cap W_{k}\) and \(A \cap W_{k}^{r}\) for every \(k \in \{ 0,1,3,5,\ldots \}\). Obviously, \(q\! \rightarrow \! x \in A\mathop{-}\limits ^{.}q\) for every x ∈ A. Furthermore, \(\neg p_{n} \vee \neg p_{m} \in A\mathop{-}\limits ^{.}q\) for every n ≠ m. Informally speaking, \(A\mathop{-}\limits ^{.}q\) contains the information that exactly one proposition p k , for \(k \in \{ 0,1,3,5,\ldots \}\), is true. But this cannot be expressed in our first-order propositional language. Note in particular that \(A\mathop{-}\limits ^{.}q\) does not contain any finite disjunction of p i ’s.
The greatest elements of A ⊥ r are \(A \cap W_{j}\) and \(A \cap W_{j}^{q}\) for every \(j \in \{ 0,2,4,6,\ldots \}\). The information contained in \(A\mathop{-}\limits ^{.}r\) is analogous with that in \(A\mathop{-}\limits ^{.}q\), with the even positive integers playing the role of the odd ones in the previous case.
We find that \(A\mathop{-}\limits ^{.}q\) and \(A\mathop{-}\limits ^{.}r\) do not even jointly imply p 0. For consider the maximally consistent set W ∗ containing \(\neg p_{i}\) for every i ≥ 0, together with \(\neg q\) and \(\neg r\). Considering what we have just said about \(A\mathop{-}\limits ^{.}q\) and \(A\mathop{-}\limits ^{.}r\), it becomes clear that W ∗ contains both of these contracted theories, as well as \(\neg p_{0}\).
Since \(p_{0} \in A\mathop{-}\limits ^{.}(q \wedge r)\) but \(p_{0}\notin Cn(A\mathop{-}\limits ^{.}q \cup A\mathop{-}\limits ^{.}r)\), we have a violation of (\(\mathop{-}\limits ^{.}8r\)).
Proof of Lemma 9.
We show that for every M ∈ A ⊥ x,
-
(i)
M is maximal in A ⊥ x under
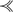
is equivalent to
-
(ii)
\(N \subseteq M\) for some N which is maximal in B ⊥ xn under
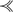 .
.(i) implies (ii): (i) means that M is such that for no M′ and i it holds that
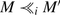 . Now take \(N = M \cap B\). We have to show that Nn is maximal in B ⊥ x. First, it is clear that \(N\nvdash x\). Next, we verify that N is a maximal subset of B which does not imply x. Suppose there is a y ∈ B − N such that \(N \cup \{ y\}\nvdash x\), but then, with y ∈ B
k
, \(N_{\geq k} \cup \{ y\}\nvdash x\). So there would be a superset M′ of \(N_{\geq k} \cup \{ y\}\) in A ⊥ x for which
. Now take \(N = M \cap B\). We have to show that Nn is maximal in B ⊥ x. First, it is clear that \(N\nvdash x\). Next, we verify that N is a maximal subset of B which does not imply x. Suppose there is a y ∈ B − N such that \(N \cup \{ y\}\nvdash x\), but then, with y ∈ B
k
, \(N_{\geq k} \cup \{ y\}\nvdash x\). So there would be a superset M′ of \(N_{\geq k} \cup \{ y\}\) in A ⊥ x for which 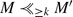 , contradicting (i). Finally, we have to show that there is no N′ ∈ B ⊥ x which is better than N under
, contradicting (i). Finally, we have to show that there is no N′ ∈ B ⊥ x which is better than N under 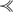 . But by the same argument as just used, it is impossible that there be some y ∈ B
k
such that y ∈ N′ − N and
. But by the same argument as just used, it is impossible that there be some y ∈ B
k
such that y ∈ N′ − N and 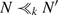 .
.(ii) implies (i): Suppose for reductio that (ii) but not (i). By the latter, there is an M′ such that
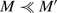 . But then
. But then 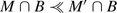 . Take, on the other hand, the N from (ii). Since \(N \subseteq M \cap B\), we have
. Take, on the other hand, the N from (ii). Since \(N \subseteq M \cap B\), we have 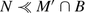 . But since \(M' \cap B\nvdash x\), N cannot be maximal in B ⊥ x, contradicting (ii). q.e.d.
. But since \(M' \cap B\nvdash x\), N cannot be maximal in B ⊥ x, contradicting (ii). q.e.d.
Re section “The Logic of Prioritized Base Contractions in the Finite Case”: Illustration of the counterexample to ( \(\mathop{-}\limits ^{.}8r\) ) in straightforward prioritized base contractions and its solution by the official definition. Let \(B =\{ (p \wedge q) \vee (p \wedge r) \vee (q \wedge r),\ r\! \rightarrow \! (p\leftrightarrow q),\ q \wedge (p\leftrightarrow r),\ p \wedge r\}\), A = Cn(B), \(A\mathop{-}\limits ^{.}{}'x\ =\ \bigcap \;\{ Cn(N)\!: N \in \gamma (B\perp x)\}\) and \(A\mathop{-}\limits ^{.}x\ =\ \bigcap \;\{ Cn(N \cup \{ x\! \rightarrow \! a\})\!: N \in \gamma (B\perp x)\}\). See Fig. 16.4
Re section “The Logic of Prioritized Base Contractions in the Finite Case”: Example illustrating how prioritized belief bases can be replaced by simple ones.
Consider the propositional language L over the two atoms p and q. Let the belief base contain the propositions p and p → q. We contrast the prioritizations \(\langle \{p\! \rightarrow \! q\},\{p\}\rangle\) and \(\langle \{p\},\{p\! \rightarrow \! q\}\rangle\). In the former case, \(B = \mathcal{B}(\mathcal{P}(\langle \{p\! \rightarrow \! q\},\{p\}\rangle )) =\{ p \wedge q,p,p \vee q,q\! \rightarrow \! p\}\), while in the latter case, \(B' = \mathcal{B}(\mathcal{P}(\langle \{p\},\{p\! \rightarrow \! q\}\rangle )) =\{ p \wedge q,q,p\! \leftrightarrow \! q,\top \}\).
In Figs. 16.5 and 16.6, “\(\left (\begin{array}{c} x\\ y \\ z \end{array} \right )\)” should be read as “\(A\mathop{-}\limits ^{.}x = Cn(y)\) according to prioritized base contraction, while \(A\mathop{-}\limits ^{.}x = Cn(z)\) according to the corresponding simple base contraction”. In the last two lines, the left argument of ‘∧’ comes from straightforward base contraction and the right argument is the recovery-guaranteeing appendage used in our official definition of prioritized base contractions.
Remarks.
Prioritized and corresponding simple base contractions indeed lead to the same results—as they should, according to the proof of Theorem 7. But note that the recovery-guaranteeing appendage is essential in quite a few cases. As for the contraction function \(\mathop{-}\limits ^{.}\), the differences in prioritization are effective only in the case of \(A\mathop{-}\limits ^{.}(p \wedge q)\), \(A\mathop{-}\limits ^{.}q\) and \(A\mathop{-}\limits ^{.}(p \leftrightarrow q)\).
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Rott, H. (2016). Belief Contraction in the Context of the General Theory of Rational Choice. In: Arló-Costa, H., Hendricks, V., van Benthem, J. (eds) Readings in Formal Epistemology. Springer Graduate Texts in Philosophy, vol 1. Springer, Cham. https://doi.org/10.1007/978-3-319-20451-2_16
Download citation
DOI: https://doi.org/10.1007/978-3-319-20451-2_16
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-20450-5
Online ISBN: 978-3-319-20451-2
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)



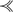
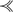 .
.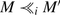 . Now take
. Now take 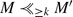 , contradicting (i). Finally, we have to show that there is no N′ ∈ B ⊥ x which is better than N under
, contradicting (i). Finally, we have to show that there is no N′ ∈ B ⊥ x which is better than N under 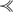 . But by the same argument as just used, it is impossible that there be some y ∈ B
k
such that y ∈ N′ − N and
. But by the same argument as just used, it is impossible that there be some y ∈ B
k
such that y ∈ N′ − N and 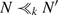 .
.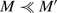 . But then
. But then 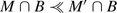 . Take, on the other hand, the N from (ii). Since
. Take, on the other hand, the N from (ii). Since 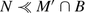 . But since
. But since 

