Abstract
We review different aspects of the superconformal index of \(\mathcal{N}=2\) superconformal theories of class \(\mathcal{S}\). In particular we discuss the relation of the index of class \(\mathcal{S}\) theories to topological QFTs and integrable models, and review how this relation can be harnessed to completely determine the index. This is part of a combined review on 2d-4d relations, edited by J. Teschner.
A citation of the form [V:x] refers to article number x in this volume.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
See [V:2] in this volume for a general introduction to class \(\mathcal{S}\).
- 2.
In this review we follow the conventions of [5]. In comparing with [6, 7], the only significant change is \(j_1 \rightarrow -j_1\) in the definitions of \(j_{12}\) and \(j_{34}\). The conventions for labeling supercharges are also slightly different in these two sets of references, but notations aside all of them choose “same” supercharge to define the general index (i.e. the supercharge with quantum numbers \(E=R=-r = \frac{1}{2}\), \((j_1, j_2) = (0, -\frac{1}{2})\).
- 3.
In other dimensions the situation can be slightly more involved. For example, in three dimensions a gauge theory contains local monopole operators which have to be introduced into the index computations along with the vector multiplets.
- 4.
These are the “basic” theories. A larger list is obtained by allowing for “irregular” punctures. Further possibilities arise by decorating the UV curve with outer automorphisms twist lines , see [14].
- 5.
In some special cases, the symmetry is enhanced by additional generators which are not naturally assigned to any puncture.
- 6.
Throughout this review we will often associate punctures with flavor symmetry factors. For theories of type A this association is well motivated (although there can be two different punctures with same flavor symmetry), but one has to remember that for type D and E theories one can have non-trivial punctures with no flavor symmetry associated with them.
- 7.
This is the generic situation. The remaining possibility is that cutting the cylinder yields the connected surface \(\mathcal{C}_{g-1, s+2}\). This case can be treated analogously.
- 8.
We’ll often omit the dependence on the superconformal fugacities to avoid cluttering.
- 9.
Here we should mention that since the state-space of the QFT obtained from the index is infinite dimensional there might be in principle issues of converges when changing basis. Such complication though do not actually arise in practice in the index computations.
- 10.
The dependence on the superconformal fugacities (p, q, t) is again left implicit.
- 11.
The same will hold for functions \(\phi _\lambda ^{\Lambda }\) associated to general punctures we will define later in this section.
- 12.
We take \(n >2\) as the \(n=2\) case is trivial. For \(n=2\) there is no distinction between minimal and maximal punctures. The basic building block \(T_2\) is identified with a free hypermultiplet in the trifundamental representation of \(\textit{SU}(2)^3\). The structure constants can then be obtained directly by expanding the free hypermultiplet index.
- 13.
Comparing with (4.9), we have reabsorbed some factors of \(C_\lambda \) into wavefunctions, by setting a new normalization for the wave function of the maximal puncture,
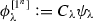 .
. - 14.
The equivalence between the realization of general punctures by superconformal tails (as sketched in the previous subsection) and the higgsing procedure that we are about to implement is explained in Sect. 12.5 of [19].
- 15.
The moment map is also an \(\textit{SU}(2)_R\) triplet and \(U(1)_r\) singlet. We consider the highest \(\textit{SU}(2)_R\) weight (which has \(R=1\)), since it is the component that contributes to the index.
- 16.
It might be that the vev actually preserves the diagonal subgroup of the UV su(2) R-symmetry and some su(2) subgroup of the flavor symmetry. In such a case there is no need for the IR enhancement of the R-symmetry. We thank C. Beem, D. Gaiotto, and A. Neitzke for pointing this out to us.
- 17.
The solution is unique up to the action of the Weyl group.
- 18.
- 19.
A 6d physical interpretation of this equation can be also entertained [24] but we will not discuss it in this review.
- 20.
This operator is called the Macdonald operator in math literature and we will shortly encounter a different incarnation of it in 4d index context.
- 21.
When writing this equation as a difference operator annihilating the partition function, it gives rise actually to the difference operator annihilating holomorphic blocks of the 3d partition function [32].
- 22.
In principle the Schur index might make sense also for non-conformal \(\mathcal{N}=2\) theories quantized on \({\mathbb S}^3 \times \mathbb {R}\), although we are not aware of a detailed analysis of the requisite deformations needed to define an \(\mathcal{N}=2\) theory on such a curved background (the analysis of [38] might be of help here). The \(\mathcal{N}=1\) analysis of [4] is not sufficient, because the Schur index cannot be understood as a special case of the \(\mathcal{N}=1\) index. Of course, in the non-conformal case one cannot relate \({\mathbb S}^3 \times \mathbb {R}\) to \(\mathbb {R}^4\) by a Weyl rescaling and there is no state/operator map.
- 23.
On a surface of finite (non-zero) area, q-YM is not topological, but it still admits a natural class \(\mathcal{S}\) interpretation [41] as the supersymmetric partition function of the (2, 0) theory on \({\mathbb S}^3\times {\mathbb S}^1\times \mathcal{C}\) where the UV curve \(\mathcal{C}\) is kept of finite area [42].
- 24.
Note that this is the same operator that we obtained in a quite different context of the reduction of the elliptic difference operator \({\mathfrak {S}}_{(0,1)}\) to three dimensions 4.34.
- 25.
To be pedantic, antichiral.
- 26.
Assuming that the Higgs branch of the 4d theory of class \(\mathcal{S}\) is isomorphic to the Higgs branch of the dimensionally reduced theory, we can consider the Coulomb index [33, 56, 57] of the mirror dual theory (see Sect. 4.5). The 3d Coulomb index of the mirror coincides with the Hilbert series of the Higgs branch of theories of class \(\mathcal{S}\) for any genus. We refer the reader to [33] for further discussion of this issue.
- 27.
The fact that the Coulomb branch is freely generated is known to be true by inspection for theories of class \(\mathcal{S}\) of type A we discuss here, but is not obvious for theories of type D and E: it would be interesting to clarify this issue. We thank Y. Tachikawa for this comment.
- 28.
The index of theories of class \(\mathcal{S}\) in presence of codimension two defects of the 6d theory wrapping the Riemann surface [68] has not been analyzed yet.
- 29.
See however [77] for some recent discussion.
- 30.
We follow the R-charge conventions of DO.
References
Romelsberger, C.: Counting chiral primaries in N \(=\) 1, d \(=\) 4 superconformal field theories. Nucl. Phys. B747, 329–353 (2006). arXiv:hep-th/0510060
Kinney, J., Maldacena, J.M., Minwalla, S., Raju, S.: An index for 4 dimensional super conformal theories. Commun. Math. Phys. 275, 209–254 (2007). arXiv:hep-th/0510251
Romelsberger, C.: Calculating the superconformal index and Seiberg duality. arXiv:0707.3702
Festuccia, G., Seiberg, N.: Rigid supersymmetric theories in curved superspace. JHEP 1106, 114 (2011). arXiv:1105.0689
Beem, C., Lemos, M., Liendo, P., Peelaers, W., Rastelli, L., et al.: Infinite chiral symmetry in four dimensions. arXiv:1312.5344
Gadde, A., Rastelli, L., Razamat, S.S., Yan, W.: Gauge theories and Macdonald polynomials. Commun. Math. Phys. 319, 147–193 (2013). arXiv:1110.3740
Gaiotto, D., Rastelli, L., Razamat, S.S.: Bootstrapping the superconformal index with surface defects. JHEP 01, 022 (2013). arXiv:1207.3577
Gadde, A., Pomoni, E., Rastelli, L.: The Veneziano limit of N \(=\) 2 superconformal QCD: towards the string dual of \(N=2 SU(N_c)\) SYM with \(N_f =2 N_c\). arXiv:0912.4918
Minahan, J.A., Nemeschansky, D.: An N \(=\) 2 superconformal fixed point with E(6) global symmetry. Nucl. Phys. B482, 142–152 (1996). arXiv:hep-th/9608047
Argyres, P.C., Seiberg, N.: S-duality in n \(=\) 2 supersymmetric gauge theories. JHEP 0712, 088 (2007)
Gadde, A., Rastelli, L., Razamat, S.S., Yan, W.: The superconformal index of the \(E_6\) SCFT. JHEP 08, 107 (2010). arXiv:1003.4244
Spiridonov, V.P., Warnaar, S.O.: Inversions of integral operators and elliptic beta integrals on root systems. Adv. Math. 207, 91–132 (2006). arXiv:math/0411044
Gaiotto, D., Neitzke, A., Tachikawa, Y.: Argyres-Seiberg duality and the Higgs branch. Commun. Math. Phys. 294, 389–410 (2010). arXiv:0810.4541
Tachikawa, Y.: N \(=\) 2 S-duality via outer-automorphism twists. J. Phys. A44, 182001 (2011). arXiv:1009.0339
Gadde, A., Pomoni, E., Rastelli, L., Razamat, S.S.: S-duality and 2d topological QFT. JHEP 03, 032 (2010). arXiv:0910.2225
Razamat, S.S.: On the N \(=\) 2 superconformal index and eigenfunctions of the elliptic RS model. arXiv:1309.0278
Gaiotto, D.: N \(=\) 2 dualities. arXiv:0904.2715
Gaiotto, D., Razamat, S.S.: Exceptional indices. JHEP 1205, 145 (2012). arXiv:1203.5517
Tachikawa, Y.: N \(=\) 2 supersymmetric dynamics for dummies. arXiv:1312.2684
Gadde, A., Gukov, S.: 2d index and surface operators. JHEP 1403, 080 (2014). arXiv:1305.0266
Alday, L.F., Gaiotto, D., Tachikawa, Y.: Liouville correlation functions from four-dimensional gauge theories. Lett. Math. Phys. 91, 167–197 (2010). arXiv:0906.3219
Alday, L.F., Gaiotto, D., Gukov, S., Tachikawa, Y., Verlinde, H.: Loop and surface operators in N \(=\) 2 gauge theory and Liouville modular geometry. JHEP 01, 113 (2010). arXiv:0909.0945
Teschner, J.: On the Liouville three point function. Phys. Lett. B363, 65–70 (1995). arXiv:hep-th/9507109
Gaiotto, D., Rastelli, L., Razamat, S.S.: Un-published
Benini, F., Tachikawa, Y., Xie, D.: Mirrors of 3d Sicilian theories. JHEP 09, 063 (2010). arXiv:1007.0992
Gaiotto, D., Witten, E.: S-duality of boundary conditions in N \(=\) 4 super Yang-Mills theory. arXiv:0807.3720
Dolan, F., Spiridonov, V., Vartanov, G.: From 4d superconformal indices to 3d partition functions. arXiv:1104.1787
Gadde, A., Yan, W.: Reducing the 4d index to the \(S^3\) partition function. JHEP 1212, 003 (2012). arXiv:1104.2592
Imamura, Y.: Relation between the 4d superconformal index and the \(S^3\) partition function. arXiv:1104.4482
Aharony, O., Razamat, S.S., Seiberg, N., Willett, B.: 3d dualities from 4d dualities. JHEP 1307, 149 (2013) arXiv:1305.3924
Nishioka, T., Tachikawa, Y., Yamazaki, M.: 3d partition function as overlap of wavefunctions. JHEP 1108, 003 (2011). arXiv:1105.4390
Beem, C., Dimofte, T., Pasquetti, S.: Holomorphic blocks in three dimensions. arXiv:1211.1986
Razamat, S.S., Willett, B.: Down the rabbit hole with theories of class S. arXiv:1403.6107
Hosomichi, K., Lee, S., Park, J.: AGT on the S-duality wall. JHEP 1012, 079 (2010). arXiv:1009.0340
Bullimore, M., Fluder, M., Hollands, L., Richmond, P.: The superconformal index and an elliptic algebra of surface defects. arXiv:1401.3379
Gorsky, A.: Integrable many-body systems in the field theories. Theor. Math. Phys. 103, 681–700 (1995). doi:10.1007/BF02065867
Gorsky, A., Nekrasov, N.: Hamiltonian systems of Calogero type and two-dimensional Yang-Mills theory. Nucl. Phys. B414, 213–238 (1994). arXiv:hep-th/9304047
Klare, C., Zaffaroni, A.: Extended supersymmetry on curved spaces. JHEP 1310, 218 (2013) arXiv:1308.1102
Dolan, F.A., Osborn, H.: On short and semi-short representations for four dimensional superconformal symmetry. Ann. Phys. 307, 41–89 (2003). arXiv:hep-th/0209056
Gadde, A., Rastelli, L., Razamat, S.S., Yan, W.: The 4d superconformal index from q-deformed 2d Yang-Mills. Phys. Rev. Lett. 106, 241602 (2011). arXiv:1104.3850
Tachikawa, Y.: 4d partition function on \(S^1 \times S^3\) and 2d Yang-Mills with nonzero area. PTEP 2013, 013B01 (2013). arXiv:1207.3497
Gaiotto, D., Moore, G.W., Tachikawa, Y.: On \({6d\,N} = {\rm (2, 0)}\) theory compactified on a Riemann surface with finite area. arXiv:1110.2657
Aganagic, M., Ooguri, H., Saulina, N., Vafa, C.: Black holes, q-deformed 2d Yang-Mills, and non-perturbative topological strings. Nucl. Phys. B715, 304–348 (2005). arXiv:hep-th/0411280
Kawano, T., Matsumiya, N.: 5D SYM on 3D sphere and 2D YM. Phys. Lett. B716, 450–453 (2012). arXiv:1206.5966
Fukuda, Y., Kawano, T., Matsumiya, N.: 5D SYM and 2D q-deformed YM. Nucl. Phys. B869, 493–522 (2013). arXiv:1210.2855
Witten, E.: On quantum gauge theories in two-dimensions. Commun. Math. Phys. 141, 153–209 (1991)
Alday, L.F., Bullimore, M., Fluder, M., Hollands, L.: Surface defects, the superconformal index and q-deformed Yang-Mills. arXiv:1303.4460
Razamat, S.S.: On a modular property of N \(=\) 2 superconformal theories in four dimensions. JHEP 1210, 191 (2012). arXiv:1208.5056
Macdonald, I.G.: Symmetric Functions and Hall Polynomials. Oxford University Press, Oxford (1995)
Mekareeya, N., Song, J., Tachikawa, Y.: 2d TQFT structure of the superconformal indices with outer-automorphism twists. JHEP 1303, 171 (2013). arXiv:1212.0545
Aganagic, M., Shakirov, S.: Knot homology from refined Chern-Simons theory. arXiv:1105.5117
Gray, J., Hanany, A., He, Y.-H., Jejjala, V., Mekareeya, N.: SQCD: a geometric apercu. JHEP 0805, 099 (2008). arXiv:0803.4257
Hanany, A., Mekareeya, N.: Counting gauge invariant operators in SQCD with classical gauge groups. JHEP 0810, 012 (2008). arXiv:0805.3728
Hanany, A., Mekareeya, N., Razamat, S.S.: Hilbert series for moduli spaces of two instantons. JHEP 1301, 070 (2013). arXiv:1205.4741
Keller, C.A., Song, J.: Counting exceptional instantons. JHEP 1207, 085 (2012). arXiv:1205.4722
Cremonesi, S., Hanany, A., Mekareeya, N., Zaffaroni, A.: Coulomb branch Hilbert series and Hall-Littlewood polynomials. arXiv:1403.0585
Cremonesi, S., Hanany, A., Mekareeya, N., Zaffaroni, A.: Coulomb branch Hilbert series and three dimensional Sicilian theories. arXiv:1403.2384
Lemos, M., Peelaers, W., Rastelli, L.: The superconformal index of class \(S\) theories of type \(D\). JHEP 1405, 120 (2014). arXiv:1212.1271
Chacaltana, O., Distler, J., Trimm, A.: Tinkertoys for the twisted D-series. arXiv:1309.2299
Chacaltana, O., Distler, J., Trimm, A.: Tinkertoys for the \(E_6\) theory. arXiv:1403.4604
Bah, I., Beem, C., Bobev, N., Wecht, B.: Four-dimensional SCFTs from M5-branes. JHEP 1206, 005 (2012). arXiv:1203.0303
Beem, C., Gadde, A.: The \(N=1\) superconformal index for class \(S\) fixed points. JHEP 1404, 036 (2014). arXiv:1212.1467
Gadde, A., Maruyoshi, K., Tachikawa, Y., Yan, W.: New N \(=\) 1 dualities. JHEP 1306, 056 (2013). arXiv:1303.0836
Agarwal, P., Song, J.: New N \(=\) 1 dualities from M5-branes and outer-automorphism twists. JHEP 1403, 133 (2014). arXiv:1311.2945
Dimofte, T., Gaiotto, D., Gukov, S.: 3-manifolds and 3d indices. arXiv:1112.5179
Gang, D., Koh, E., Lee, K.: Line operator index on \(S^1\times S^3\). arXiv:1201.5539
Gang, D., Koh, E., Lee, K.: Superconformal index with duality domain wall. JHEP 1210, 187 (2012). arXiv:1205.0069
Alday, L.F., Tachikawa, Y.: Affine SL(2) conformal blocks from 4d gauge theories. Lett. Math. Phys. 94, 87–114 (2010). arXiv:1005.4469
van de Bult, F.: An elliptic hypergeometric integral with \(w(f_4)\) symmetry. Ramanujan J. 25, 1–20 (2011). arXiv:0909.4793
Beem, C., Peelaers, W., Rastelli, L., van Rees, B.C.: Chiral algebras of class S. arXiv:1408.6522
Benini, F., Nishioka, T., Yamazaki, M.: 4d index to 3d index and 2d TQFT. arXiv:1109.0283
Alday, L.F., Bullimore, M., Fluder, M.: On S-duality of the superconformal index on lens spaces and 2d TQFT. arXiv:1301.7486
Razamat, S.S., Yamazaki, M.: S-duality and the N \(=\) 2 lens space index. JHEP 1310, 048 (2013). arXiv:1306.1543
Closset, C., Dumitrescu, T.T., Festuccia, G., Komargodski, Z.: The geometry of supersymmetric partition functions. JHEP 1401, 124 (2014). arXiv:1309.5876
Closset, C., Shamir, I.: The \({\cal {N}}=1\) chiral multiplet on \(T^2 \times S^2\) and supersymmetric localization. JHEP 1403, 040 (2014). arXiv:1311.2430
Xie, D.: General Argyres-Douglas theory. JHEP 1301, 100 (2013). arXiv:1204.2270
Del Zotto, M., Hanany, A.: Complete graphs, Hilbert series, and the Higgs branch of the 4d N \(=\) SCFT’s. arXiv:1403.6523
Yoshida, Y.: Factorization of 4d N \(=\) 1 superconformal index. arXiv:1403.0891
Peelaers, W.: Higgs branch localization of \({\cal {N}} = 1\) theories on \(S^3 \times S^1\). arXiv:1403.2711
Pasquetti, S.: Factorisation of N \(=\) 2 theories on the squashed 3-sphere. JHEP 1204, 120 (2012). arXiv:1111.6905
Cecotti, S., Gaiotto, D., Vafa, C.: \(tt^*\) geometry in 3 and 4 dimensions. JHEP 1405, 055 (2014). arXiv:1312.1008
Spiridonov, V., Vartanov, G.: Elliptic hypergeometric integrals and ’t Hooft anomaly matching conditions. JHEP 1206, 016 (2012). arXiv:1203.5677
Di Pietro, L., Komargodski, Z.: Cardy Formulae for SUSY theories in d \(=\) 4 and d \(=\) 6. arXiv:1407.6061
Ardehali, A.A., Liu, J.T., Szepietowski, P.: Central charges from the \({\cal {N}} = 1\) superconformal index. arXiv:1411.5028
Buican, M., Nishinaka, T., Papageorgakis, C.: Constraints on chiral operators in \( {\cal N}=2\). JHEP 12, 095 (2014). doi:10.1007/JHEP12(2014)095
Dobrev, V., Petkova, V.: All positive energy unitary irreducible representations of extended conformal supersymmetry. Phys. Lett. B162, 127–132 (1985)
Acknowledgments
It is a great pleasure to thank Chris Beem, Abhijit Gadde, Davide Gaiotto, Madalena Lemos, Pedro Liendo, Wolfger Peelaers, Elli Pomoni, Brian Willett, and Wenbin Yan, for very enjoyable collaboration and countless discussions on the material reviewed here. We thank Davide Gaiotto and Yuji Tachikawa for useful comments on the draft. LR thanks the Simons Foundation and the Solomon Guggenheim Foundation for their generous support. He is grateful to the IAS, Princeton, and to the KITP, Santa Barbara, for their wonderful hospitality during his sabbatical leave. LR is also supported in part by the National Science Foundation under Grant No. NSF PHY1316617. SSR gratefully acknowledges support from the Martin A. Chooljian and Helen Chooljian membership at the Institute for Advanced Study. The research of SSR was also partially supported by National Science Foundation under Grant No. PHY-0969448, and by “Research in Theoretical High Energy Physics” grant DOE-SC00010008. SSR would like to thank KITP, Santa Barbara, and the Simons Center, Stony Brook, for hospitality and support during different stages of this work.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix 1: Plethystics
In this appendix we collect the definitions of some special functions and combinatorial objects used in the bulk of the review. The Pochammer symbol is defined as

The theta-function is given by

The plethystic exponential is given by

In particular
The inverse of the plethystic exponential is the logarithm, given by

where \(\mu (\ell )\) is the Mobius mu-function. Finally the elliptic Gamma function is defined as

Appendix 2: \(\mathcal{N}=2\) Superconformal Representation Theory
In this appendix (adapted from [5]) we review the classification of short representations of the four-dimensional \(\mathcal {N}=2\) superconformal algebra [2, 39, 86].
Short representations occur when the norm of a superconformal descendant state in what would otherwise be a long representation is rendered null by a conspiracy of quantum numbers. The unitarity bounds for a superconformal primary operator are given by
where we have defined
and short representations occur when one or more of these bounds are saturated. The different ways in which this can happen correspond to different combinations of Poincaré supercharges that will annihilate the superconformal primary state in the representation. There are two types of shortening conditions, each of which has four incarnations corresponding to an \(\textit{SU}(2)_R\) doublet’s worth of conditions for each supercharge chirality:




The different admissible combinations of shortening conditions that can be simultaneously realized by a single unitary representation are summarized in Table 4, where the reader can also find the precise relations that must be satisfied by the quantum numbers \((E,j_1,j_2,r,R)\) of the superconformal primary operator, as well as the notations used to designate the different representations in [39] (DO) and [2] (KMMR).Footnote 30
At the level of group theory, it is possible for a collection of short representations to recombine into a generic long representation whose dimension is equal to one of the unitarity bounds of (8.7). In the DO notation, the generic recombinations are as follows:



There are special cases when the quantum numbers of the long multiplet at threshold are such that some Lorentz quantum numbers in (8.13) would be negative and unphysical:





The last three recombinations involve multiplets that make an appearance in the associated chiral algebra described in this work. Note that the \(\mathcal {E}\), \(\bar{\mathcal {E}}\), \(\hat{\mathcal{B}}_{\frac{1}{2}}\), \(\hat{\mathcal{B}}_{1}\), \(\hat{\mathcal{B}}_{\frac{3}{2}}\), \(\mathcal {D}_0\), \(\bar{\mathcal {D}}_0\), \(\mathcal {D}_{\frac{1}{2}}\) and \(\bar{\mathcal {D}}_{\frac{1}{2}}\) multiplets can never recombine, along with \(\mathcal {B}_{\frac{1}{2},r(0,j_2)}\) and \(\bar{\mathcal {B}}_{\frac{1}{2},r(j_1,0)}\).
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Rastelli, L., Razamat, S.S. (2016). The Superconformal Index of Theories of Class \(\mathcal {S}\) . In: Teschner, J. (eds) New Dualities of Supersymmetric Gauge Theories. Mathematical Physics Studies. Springer, Cham. https://doi.org/10.1007/978-3-319-18769-3_9
Download citation
DOI: https://doi.org/10.1007/978-3-319-18769-3_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-18768-6
Online ISBN: 978-3-319-18769-3
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


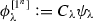 .
.